Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:porown1grpl:nparpl:chigoodnespl
The Chi-square goodness-of-fit test
The  test (goodnes-of-fit) is also called the one sample
test (goodnes-of-fit) is also called the one sample  test and is used to test the compatibility of values observed for
test and is used to test the compatibility of values observed for  (
(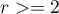 ) categories
) categories 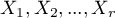 of one feature
of one feature  with hypothetical expected values for this feature. The values of all
with hypothetical expected values for this feature. The values of all  measurements should be gathered in a form of a table consisted of
measurements should be gathered in a form of a table consisted of  rows (categories:
rows (categories: 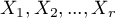 ). For each category
). For each category 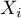 there is written the frequency of its occurence
there is written the frequency of its occurence 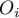 , and its expected frequency
, and its expected frequency 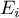 or the probability of its occurence
or the probability of its occurence 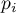 . The expected frequency is designated as a product of
. The expected frequency is designated as a product of 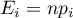 . The built table can take one of the following forms:
. The built table can take one of the following forms:
![LaTeX \begin{tabular}[t]{c@{\hspace{1cm}}c}
\begin{tabular}{c|c c}
$X_i$ categories& $O_i$ & $E_i$ \\\hline
$X_1$ & $O_1$ & $E_i$ \\
$X_2$ & $O_2$ & $E_2$ \\
... & ... & ...\\
$X_r$ & $O_r$ & $E_r$ \\
\end{tabular}
&
\begin{tabular}{c|c c}
$X_i$ categories& $O_i$ & $p_i$ \\\hline
$X_1$ & $O_1$ & $p_1$ \\
$X_2$ & $O_2$ & $p_2$ \\
... & ... & ...\\
$X_r$ & $O_r$ & $p_r$ \\
\end{tabular}
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img77385665f77e4a4583e9d51979a49d71.png)
Basic assumptions:
- measurement on a nominal scale - any order is not taken into account,
- large expected frequencies (according to the Cochran interpretation (1952)1),
- observed frequencies total should be exactly the same as an expected frequencies total, and the total of all
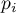 probabilities should come to 1.
probabilities should come to 1.
Hypotheses:
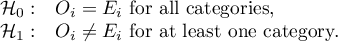
Test statistic is defined by:
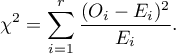
This statistic asymptotically (for large expected frequencies) has the Chi-square distribution with the number of degrees of freedom calculated using the formula: 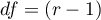 .
.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Chi-square test (goodness-of-fit) can be opened in Statistics menu → NonParametric tests (unordered categories)→Chi-square (goodnes-of-fit) or in ''Wizard''.
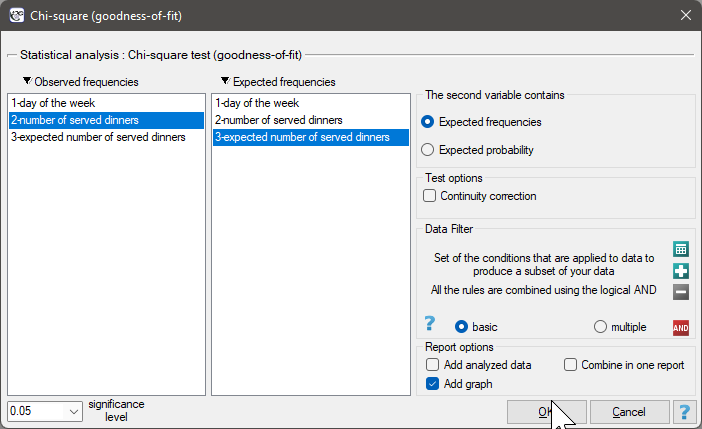
We would like to get to know if the number of dinners served in some school canteen within a given frame of time (from Monday to Friday) is statistically the same. To do this, there was taken a one-week-sample and written the number of served dinners in the particular days: Monday - 33, Tuesday - 29, Wednesday - 32, Thursday -36, Friday - 20.
As a result there were 150 dinners served in this canteen within a week (5 days).
We assume that the probability of serving dinner each day is exactly the same, so it comes to 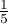 . The expected frequencies of served dinners for each day of the week (out of 5) comes to
. The expected frequencies of served dinners for each day of the week (out of 5) comes to 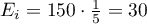 .
.
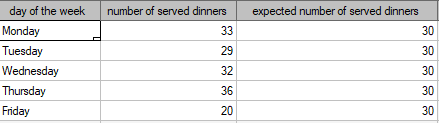
Hypotheses:

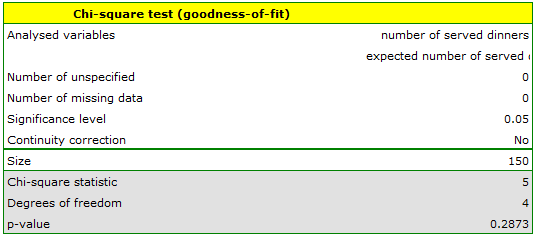
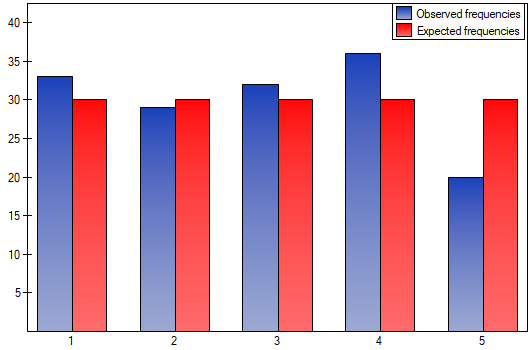
The p-value from the  distribution with 4 degrees of freedom comes to 0.2873. So using the significance level
distribution with 4 degrees of freedom comes to 0.2873. So using the significance level  you can estimate that there is no reason to reject the null hypothesis that informs about the compatibility of the number of served dinners with the expected number of dinners served within the particular days.
you can estimate that there is no reason to reject the null hypothesis that informs about the compatibility of the number of served dinners with the expected number of dinners served within the particular days.
Note!
If you want to make more comparisons within the framework of a one research, it is possible to use the Bonferroni correction2). The correction is used to limit the size of I type error, if we compare the observed frequencies and the expected ones between particular days, for example:
Friday  Monday,
Monday,
Friday  Tuesday,
Tuesday,
Friday  Wednesday,
Wednesday,
Friday  Thursday,
Thursday,
Provided that, the comparisons are made independently. The significance level  for each comparison must be calculated according to this correction using the following formula:
for each comparison must be calculated according to this correction using the following formula: 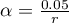 , where
, where  is the number of executed comparisons. The significance level for each comparison according to the Bonferroni correction (in this example) is
is the number of executed comparisons. The significance level for each comparison according to the Bonferroni correction (in this example) is 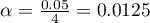 .
.
However, it is necessary to remember that if you reduce  for each comparison, the power of the test is increased.
for each comparison, the power of the test is increased.
en/statpqpl/porown1grpl/nparpl/chigoodnespl.txt · ostatnio zmienione: 2022/02/11 18:18 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

