PQStat - Baza Wiedzy

Verification of statistical hypotheses

To verify a statistical hypotheses, follow several steps:

The 1st step: Make a hypotheses, which can be verified by means of statistical tests.

Each statistical test gives you a general form of the null hypothesis 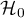$\mathcal{H}_0$ and the alternative one $\mathcal{H}_1$ :

$\begin{array}{cl} \mathcal{H}_0: & \textrm{there is \textbf{no} statistically significant \textbf{difference} among \textbf{populations}}\\ &\textrm{(means, medians, proportions distributions etc.)},\\\\ \mathcal{H}_1: & \textrm{there \textbf{is} a statistically significant \textbf{difference} among \textbf{populations}}\\ &\textrm{(means, medians, proportions, distributions etc.)}. \end{array}$

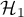Researcher must formulate the hypotheses in the way, that it is compatible with the reality and statistical test requirements, for example:

$\begin{array}{cl} \mathcal{H}_0: & \textrm{the percentage of women and men running their own businesses }\\ &\textrm{in an analysed population is exactly the same}. \end{array}$

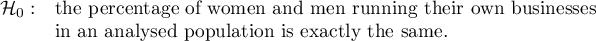
If you do not know, which percentage (men or women) in an analysed population might be greater, the alternative hypothesis should be two-sided. It means you should not assume the direction:

$\begin{array}{cl} \mathcal{H}_1: & \textrm{the percentage of women and men running their own businesses}\\ &\textrm{in an analysed population is different}. \end{array}$

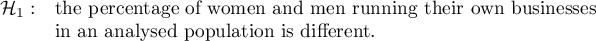
It may happen (but very rarely) that you are sure you know the direction in an alternative hypothesis. In this case you can use one-sided alternative hypothesis.

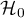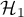The 2nd step: Verify which of the hypotheses $\mathcal{H}_0$ or $\mathcal{H}_1$ is more probable. Depending on the kind of an analysis and a type of variables you should choose an appropriate statistical test.

Note 1

Note, that choosing a statistical test means mainly choosing an appropriate measurement scale (interval, ordinal, nominal scale) which is represented by the data you want to analyse. It is also connected with choosing the analysis model (dependent or independent)

Measurements of the given feature are called dependent (paired), when they are made a couple of times for the same objects. When measurements of the given feature are performed on the objects which belong to different groups, these groups are called independent (unpaired) measurements.

Some examples of researches in dependent groups:

Examining a body mass of patients before and after a slimming diet, examining reaction on the stimulus within the same group of objects but in two different conditions (for example - at night and during the day), examining the compatibility of evaluating of credit capacity calculated by two different banks but for the same group of clients etc.

Some examples of researches in independent groups:

Examining a body mass in a group of healthy patients and ill ones, testing effectiveness of fertilising several different kinds of fertilisers, testing gross domestic product (GDP) sizes for the several countries etc.

Note 2

A graph which is included in the ''Wizard'' window makes the choice of an appropriate statistical test easier.

Test statistic of the selected test calculated according to its formula is connected with the adequate theoretical distribution.

$\psset{xunit=1.25cm,yunit=10cm} \begin{pspicture}(-5,-0.1)(5,.5) \psline{->}(-4,0)(4.5,0) \psTDist[linecolor=green,nue=4]{-4}{4} \pscustom[fillstyle=solid,fillcolor=cyan!30]{% \psTDist[linewidth=1pt,nue=4]{-4}{-2.776445}% \psline(-2.776445,0)(-4,0)} \pscustom[fillstyle=solid,fillcolor=cyan!30]{% \psline(2.776445,0)(2.776445,0)% \psTDist[linewidth=1pt,nue=4]{2.776445}{4}% \psline(4,0)(2.776445,0)} \rput(-3.6,0.2){$\alpha/2$} \psline{->}(-3.6,0.15)(-3.1,0.04) \rput(3.6,0.2){$\alpha/2$} \psline{->}(3.6,0.15)(3,0.04) \rput(1,0.5){$1-\alpha$} \psline{->}(1,0.46)(0.55,0.35) \rput(2.5,-0.04){value of test statistics} \end{pspicture}$

The application calculates a value of test statistics and also a p-value for this statistics (a part of the area under a curve which is adequate to the value of the test statistics). The $p$ value enables you to choose a more probable hypothesis (null or alternative). But you always need to assume if a null hypothesis is the right one, and all the proofs gathered as a data are supposed to supply you with the enough number of counterarguments to the hypothesis:

$\begin{array}{ccl} $ if $ p \le \alpha & \Longrightarrow & $ reject $ \mathcal{H}_0 $ and accept $ \mathcal{H}_1, \\ $ if $ p > \alpha & \Longrightarrow & $ there is no reason to reject $ \mathcal{H}_0. \\ \end{array}$

There is usually chosen significance level $\alpha=0.05$ , accepting that for 5 % of the situations we will reject a null hypothesis if there is the right one. In specific cases you can choose other significance level for example 0.01 or 0.001.

Note

Note, that a statistical test may not be compatible with the reality in two cases:

$\begin{tabular}{|c|c||c|c|} \hline \multicolumn{2}{|c||}{}& \multicolumn{2}{|c|}{\textbf{reality}}\\\cline{3-4} \multicolumn{2}{|c||}{} & $\mathcal{H}_0:$ true& $\mathcal{H}_0:$ false\\\hline \hline \multirow{2}{*}{\textbf{test result}}& $\mathcal{H}_0:$ true & OK & $\beta$ \\\cline{2-4} & $\mathcal{H}_0:$ false& $\alpha$ & OK \\\hline \end{tabular}$

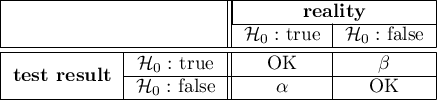
We may make two kinds of mistakes:

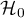$\alpha$ = 1st type of error (probability of rejecting hypothesis $\mathcal{H}_0$ , when it is the right one),

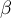$\beta$ = 2nd type of error (probability of accepting hypothesis 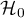$\mathcal{H}_0$ , when it is the wrong one).

Power of the test is $1 - \beta$ .

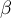Values $\alpha$ and $\beta$ are connected with each other. The approved practice is to assume the significance level in advance $\alpha$ and minimalization 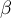$\beta$ by decreasing a sample size.

The 3rd step: Description of results of hypotheses verification.

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Verification of statistical hypotheses

Narzędzia strony