Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:przestrzenpl:lokalpl
Spis treści
Local estimate of spatial clustering
In the local analysis we try to define clusters according to their placement, size, and intensity. A cluster is understood as a limited gathering of objects of certain intensity, placed in space and/or time, an accidental appearance of which is highly improbable. If we identify such a gathering which is not accidental but is a statistically significant cluster we can infer the reasons for its occurrence.
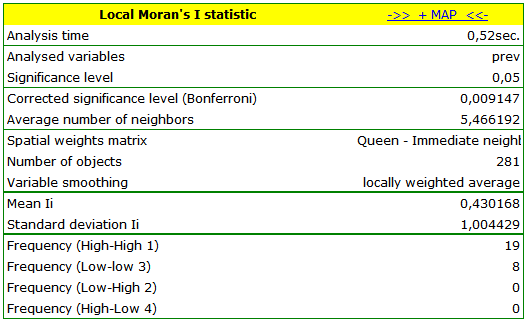
Local Moran's I statistic
Local Moran's I statistic is the most popular analysis from those defined as LISA (Local Indicators of Spatial Association) (Luc Anselin 1995 1). In contrast to Global Moran's I statistic it defines the local spacial autocorrelation, i.e. defines the similarity of a spatial unit to its neighbors and studies the statistical significance of that dependence.
Local Moran's I coefficient
The local form of Moran's 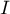 coefficient for the
coefficient for the  observation is defined with the formula:
observation is defined with the formula:
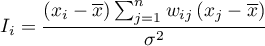
where:
 – the number of spatial objects (the number of points or polygons),
– the number of spatial objects (the number of points or polygons),
 ,
, 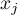 – are the values of the variable for the compared objects,
– are the values of the variable for the compared objects,
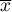 – it is the mean value of the variable for all objects,
– it is the mean value of the variable for all objects,
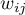 – elements of a spacial weight matrix (it is recommended that the matrix is row standardized),
– elements of a spacial weight matrix (it is recommended that the matrix is row standardized),
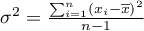 – variance
– variance
The interpretation of the local Moran's coefficient is analogous to its global counterpart, however, it largely depends on the selected weight matrix. Most often non-zero matrices are ascribed only to neighboring objects. As a result the local coefficient only describes the similarity of objects in the zone of neighborhood. Row standardization makes it easier to compare the values of coefficients obtained for various objects as the expected value for each coefficient is then the same.
High values of a coefficient point to the occurrence of clusters with similar values while low values of a coefficient point to the occurrence of the so-called hot spots, and values near the expected value 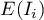 point to the random distribution in space of the studied variable.
point to the random distribution in space of the studied variable.
The expected value is defined with the formula:
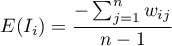
The significance of Moran's autocorrelation coefficient
By testing the statistical significance of the relationship among the neighboring objects the following hypotheses are studied:
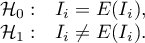
The test statistic has the form presented below:
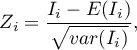
where:
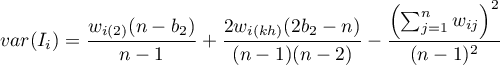 – variance in a random distribution,
– variance in a random distribution,
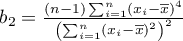 ,
,
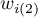 – the sum of weights square for the
– the sum of weights square for the  row,
row,
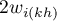 – the sum of possible weights ratios for the
– the sum of possible weights ratios for the  row, after the exclusion of ratios with the same indexes.
row, after the exclusion of ratios with the same indexes.
The 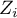 statistics has, asymptotically (for large sample sizes), rnormal distribution.
statistics has, asymptotically (for large sample sizes), rnormal distribution.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Due to the problem of a lack of independence of coefficients computed for neighboring objects it is suggested to use a corrected significance level  . The suggested corrections are: Bonferroni correction:
. The suggested corrections are: Bonferroni correction: 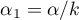 or Šidák correction:
or Šidák correction: 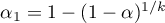 , where
, where  is the arithmetic mean number of the neighbors.
is the arithmetic mean number of the neighbors.
Map layers
The combination of information from Moran's scatter plot (the division of objects into: High-High, Low-Low, Low-High, High-Low) and from the significance of the local Moran's statistics presents on a map the so-called spatial regimes:
- Statistically significant High-High objects (objects with high values surrounded by objects with high values) are marked in red on the map;
- Statistically significant Low-Low objects (objects with low values surrounded by objects with low values) are marked in blue on the map;
- Statistically significant Low-High objects (objects with low values surrounded by objects with high values) are marked in light blue on the map;
- Statistically significant High-Low objects (objects with high values surrounded by objects with low values) are marked in light red on the map.
The window with the settings of the local Moran's analysis option is accessed via the menu Spatial analysis → Spatial statistics → Local Moran's I statistic.
EXAMPLE cont. (catalog: leukemia, file: leukemia)
We will analyze data about leukemia.
- The map
leukemiacontains information about the location of 281 polygons (census tracts) in the northern part of the state of New York. - Data for the map
leukemia:- Column
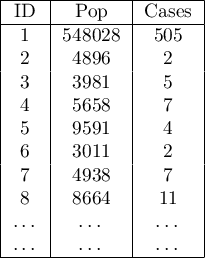
CASES– the number of cases of leukemia in the years 1978-1982, ascribed to particular objects (census tracts). The value should be an integral number, however, in agreement with Waller's (1994) description, some cases which could not be objectively ascribed to a particular region have been divided proportionately. Hence, the numerousnesses of the cases ascribed to the 281 objects are not integral numbers. - Column
POP– population size in particular objects. - Column
prev– the frequency coefficient of leukemia per 100000 people, for each object in one year: prev=(CASES/POP)*100000/5
The global analysis has not yielded an unambiguous answer as to the occurrence of spatial autocorrelation. We will, then, check if we can find regions in which the prevalence of leukemia is significantly higher.
In order to localize clusters of leukemia and regions which contrast with the environment with respect to the prevalence of that disease we will compute the local Moran's coefficient. For the analysis we will use the prev variable and the neighborhood matrix – Queen, row standardized (according to the contiguity) which is suggested by the program. In order to use a different matrix one has to generate it first, see chapter: Spatial weight matrix. We also select one of the corrections of the significance level.

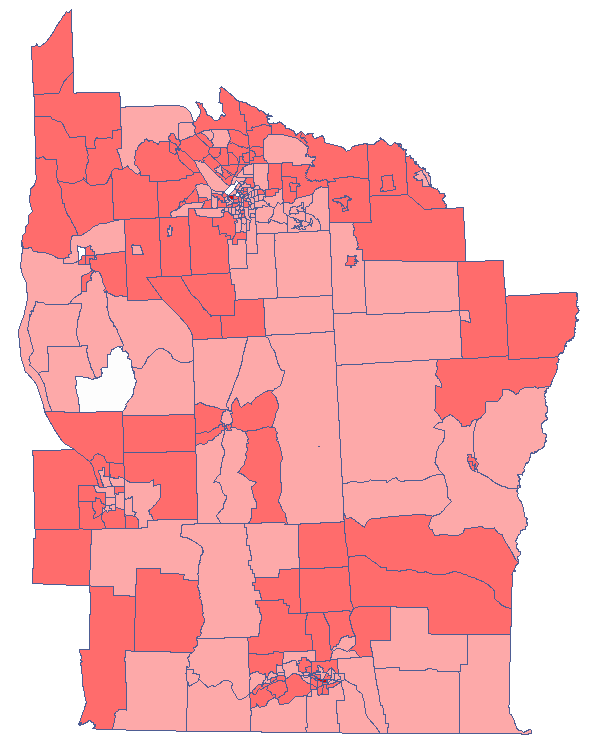
The obtained report presents the values of local coefficients, the values of test statistics, and the corresponding values of test probability. We will also find here the information about the number of regions defining the spatial regimes (High-High, Low-Low, Low-High, High-Low).
Also, a result is ascribed to the analysis, which we can draw on the map (button  ) – those are spatial regimes described in the report with the use of the color column.
) – those are spatial regimes described in the report with the use of the color column.
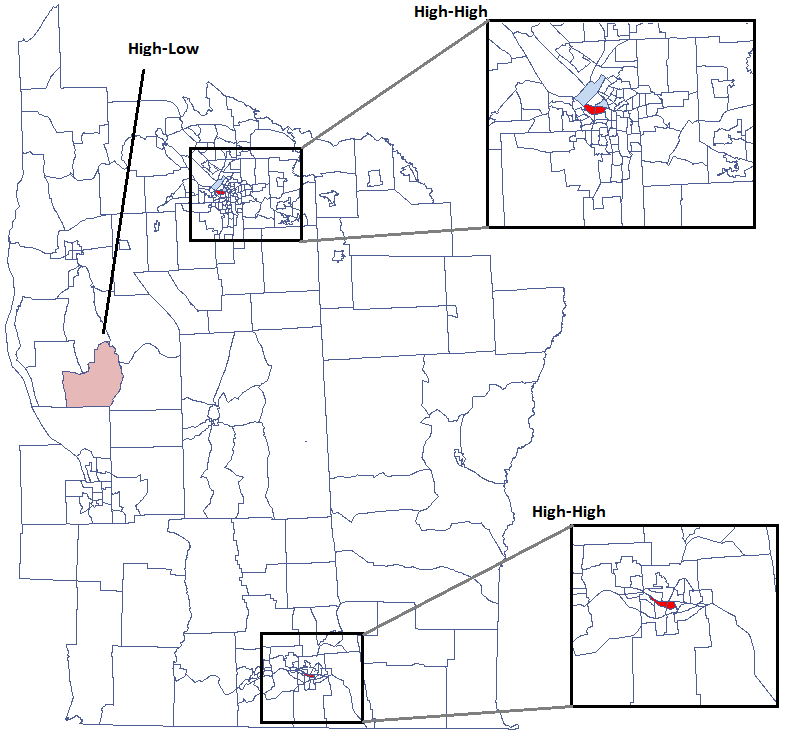
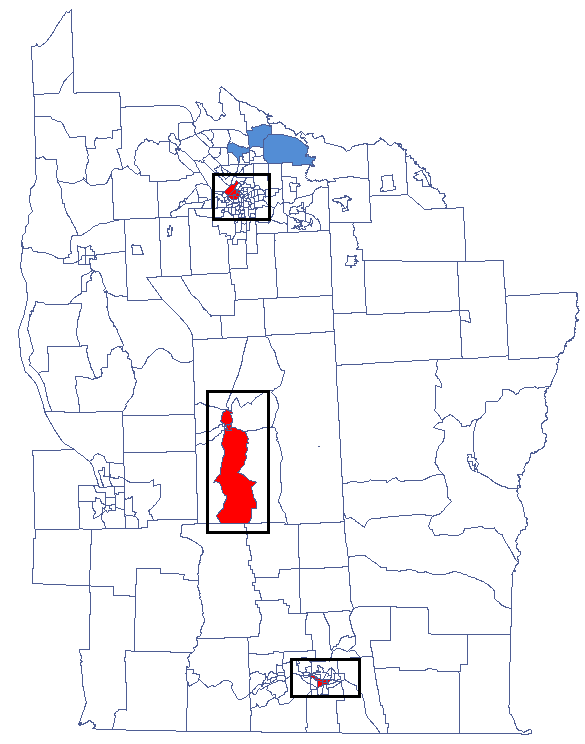
We have been able to localize small but significant clusters in which the prevalence of leukemia is higher. The red color is used for the 2 clusters (4 register regions) lying in smaller and more populated regions – they are the centers of the clusters with high leukemia values. The light red color is used for the census tract with high values of the coefficient describing the prevalence of leukemia. The region contrasts with the neighboring census tracts which are characterized by a relatively low coefficient.
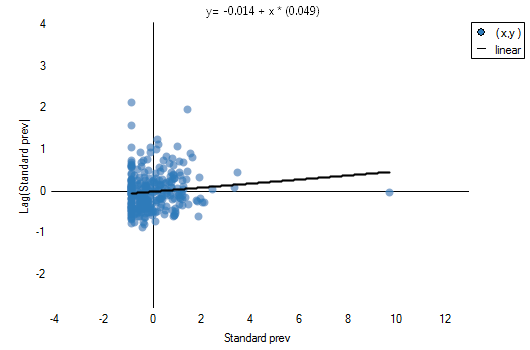
The obtained results can be further illustrated when the map is colored with the values of the local Moran's 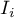 coefficient or the values of a test statistic, or
coefficient or the values of a test statistic, or  values. One just has to copy the appropriate columns from the report into a datasheet. In this example we will use the values of the
values. One just has to copy the appropriate columns from the report into a datasheet. In this example we will use the values of the 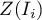 test statistic for coloring. Having pasted it into an empty column of a datasheet, in the map manager we color the base map according to the values of that column, selecting the standard deviation with the coefficient 3 as a way of gradiating colors. Positive and high values of the
test statistic for coloring. Having pasted it into an empty column of a datasheet, in the map manager we color the base map according to the values of that column, selecting the standard deviation with the coefficient 3 as a way of gradiating colors. Positive and high values of the 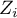 statistics point to the occurrence of clusters of similar values while negative and low values of that statistic point to the occurrence of the so-called hot spots. Values close to 0 point to a random distribution of the studied value in space.
statistics point to the occurrence of clusters of similar values while negative and low values of that statistic point to the occurrence of the so-called hot spots. Values close to 0 point to a random distribution of the studied value in space.
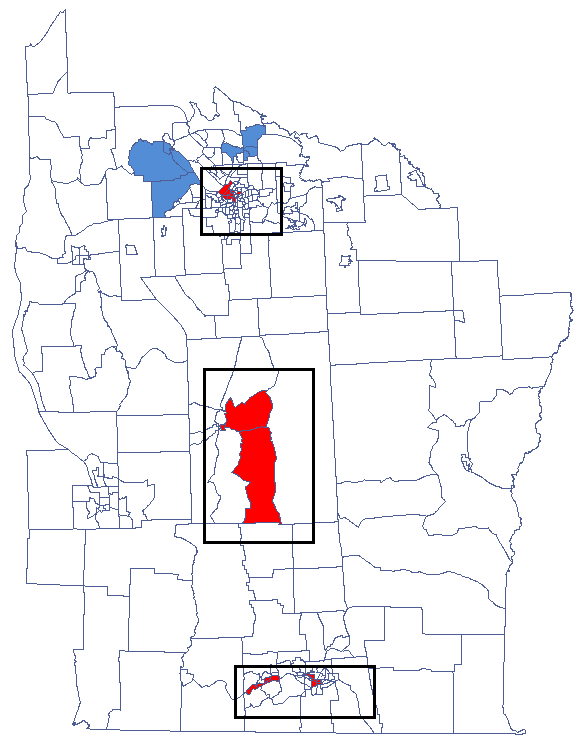
By analyzing the smoothed variable prev we strengthen the clusterization effect. We obtain a similar result but this time we localize 3 clusters (19 census tracts) which are cluster centers.
2022/02/09 12:56
Local Getis-Ord’s G statistic
Getis and Ord's 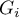 statistic (Getis and Ord 1992, Ord and Getis 1995) allows the detection of a local concentration of high and low values in neighboring objects and studies the statistical significance of that dependence. Getis and Ord have also defined a
statistic (Getis and Ord 1992, Ord and Getis 1995) allows the detection of a local concentration of high and low values in neighboring objects and studies the statistical significance of that dependence. Getis and Ord have also defined a 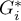 statistics, very similar to the
statistics, very similar to the 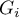 statistics. The only difference between them is that in the case of the former the object for which the study is made also takes part in the analysis. In a weight matrix, then, the so-called potential is defined for that object, i.e. the neighborhood with itself (values on the axis are greater than 0).
statistics. The only difference between them is that in the case of the former the object for which the study is made also takes part in the analysis. In a weight matrix, then, the so-called potential is defined for that object, i.e. the neighborhood with itself (values on the axis are greater than 0).
Getis-Ord’s G coefficient
The local form of Getis and Ord's 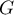 coefficient for the
coefficient for the  observation is defined with the formula:
observation is defined with the formula:
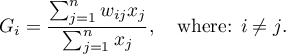
The 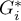 coefficient is defined with the same formula but the computations are also made for the studied object, that is the object for which the
coefficient is defined with the same formula but the computations are also made for the studied object, that is the object for which the  and the
and the  indexes are equal.
indexes are equal.
As the coefficient is based on a quotient of two sums of the values of the (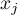 ) objects, in order to interpret the coefficient correctly it is important that the analyzed phenomenon is described with the use of positive numbers. The interpretation of Getis and Ord's local coefficient, similarly to local Moran's coefficient, depends, to a great degree, on the selected weight matrix (row standardization of the matrix is recommended). High values of the
) objects, in order to interpret the coefficient correctly it is important that the analyzed phenomenon is described with the use of positive numbers. The interpretation of Getis and Ord's local coefficient, similarly to local Moran's coefficient, depends, to a great degree, on the selected weight matrix (row standardization of the matrix is recommended). High values of the 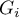 or
or 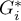 coefficients point to a concentration of objects with high values of the analyzed phenomenon, whereas low values point to a clustering of objects with low values. When the values are close to the expected value then the spatial distribution of the studied value is random.
coefficients point to a concentration of objects with high values of the analyzed phenomenon, whereas low values point to a clustering of objects with low values. When the values are close to the expected value then the spatial distribution of the studied value is random.
The expected value is defined with the formula:
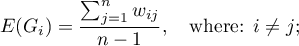
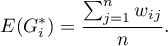
The significance of Getis and Ord's coefficient
By testing the statistical significance of the relationship among the neighboring objects the following hypotheses are studied:
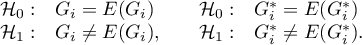
The test statistic has the form presented below:
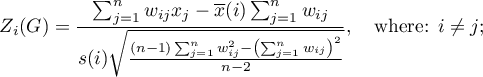
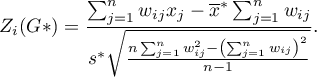
where:
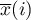 i
i 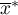 – the mean of the variable
– the mean of the variable  ,
,
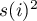 i
i 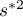 – the variance of the
– the variance of the  variable.
variable.
The 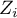 statistics has, asymptotically (for large sample sizes), normal distribution.
statistics has, asymptotically (for large sample sizes), normal distribution.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Due to the problem of a lack of independence of coefficients computed for neighboring objects it is suggested to use a corrected significance level  . The suggested corrections are: Bonferroni correction:
. The suggested corrections are: Bonferroni correction: 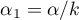 or Šidák correction:
or Šidák correction: 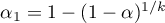 , where
, where  is the arithmetic mean number of the neighbors.
is the arithmetic mean number of the neighbors.
Map layers
The combination of the information from the value of the  statistic and its significance presents the so-called spacial regimes on the map:
statistic and its significance presents the so-called spacial regimes on the map:
- Statistically significant objects with high values of the
 statistic are marked as High-High (objects with high values surrounded by objects with high values) and marked in red on the map;
statistic are marked as High-High (objects with high values surrounded by objects with high values) and marked in red on the map; - Statistically significant objects with low values of the
 statistic are marked as Low-Low (objects with low values surrounded by objects with low values) and marked in blue on the map;
statistic are marked as Low-Low (objects with low values surrounded by objects with low values) and marked in blue on the map;
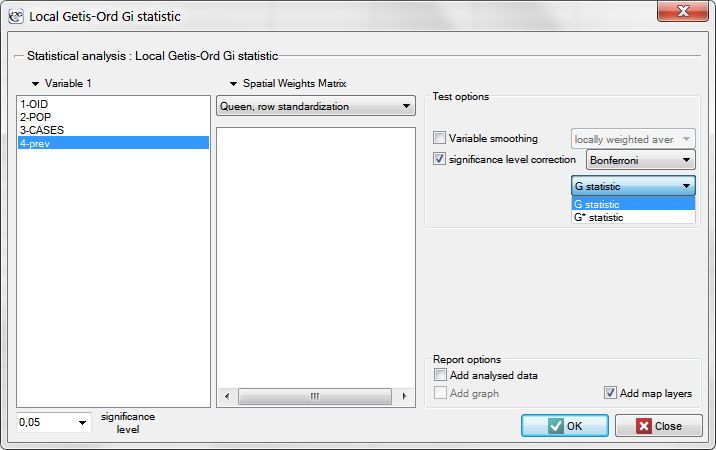
The window with settings for Local Getis and Ord's analysis is accessed via the menu Spatial analysis → Spatial statistics → Getis-Ord <latex>$G_i$</latex> statistic.
EXAMPLE con. (catalog: leukemia, file: leukemia)
We will analyze the data concerning leukemia.
- The map
leukemiacontains information about the location of 281 polygons (census tracts) in the northern part of the state of New York. - Data for the map
leukemia:- Column
CASES– the number of cases of leukemia in the years 1978-1982, ascribed to particular objects (census tracts). The value should be an integral number, however, in agreement with Waller's (1994) description, some cases which could not be objectively ascribed to a particular region have been divided proportionately. Hence, the numerousnesses of the cases ascribed to the 281 objects are not integral numbers. - Column
POP– population size in particular objects. - Column
prev– the frequency coefficient of leukemia per 100000 people, for each object in one year: prev=(CASES/POP)*100000/5
The global analysis has not yielded an unambiguous answer as to the occurrence of spatial autocorrelation. We will, then, check if we can find regions in which the prevalence of leukemia is significantly higher.
In order to localize leukemia clusters we will compute the 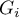 and
and 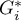 coefficients. The analysis will be conducted with the
coefficients. The analysis will be conducted with the prev variable and the neighborhood matrix – Queen, row standardized (according to contiguity) which is suggested by the program. In order to use a different matrix one has to generate it first, see chapter: Spatial weight matrix. We also select one of the corrections of the significance level.


The obtained report presents the values of local coefficients, the values of test statistics, and the corresponding values of test probability. We will also find the information about the number of regions defining the spatial regimes (High-High, Low-Low).
Also, a result is ascribed to the analysis, which we can draw on the map (button  ) – those spatial regimes are defined in the report with the use of the color column.
) – those spatial regimes are defined in the report with the use of the color column.
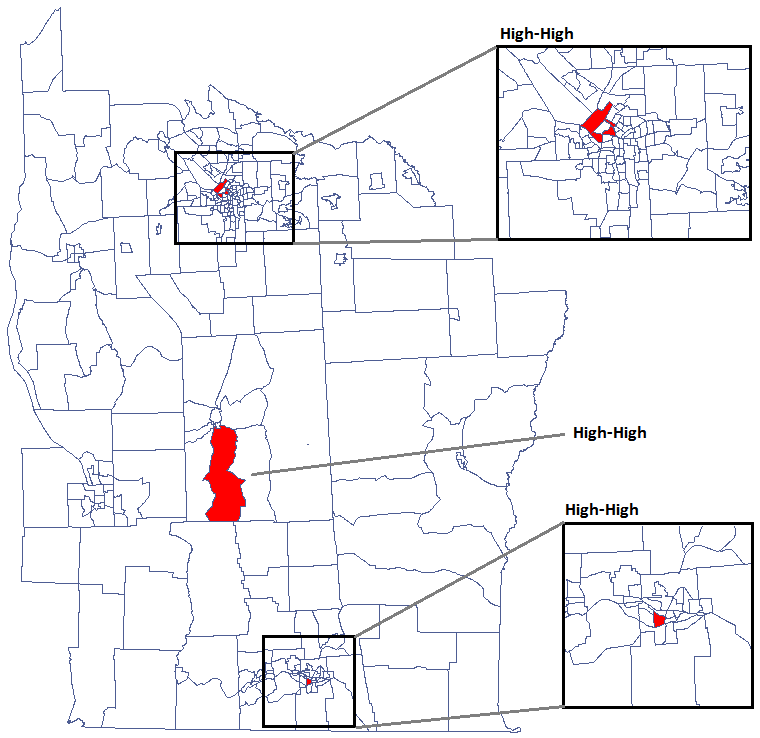
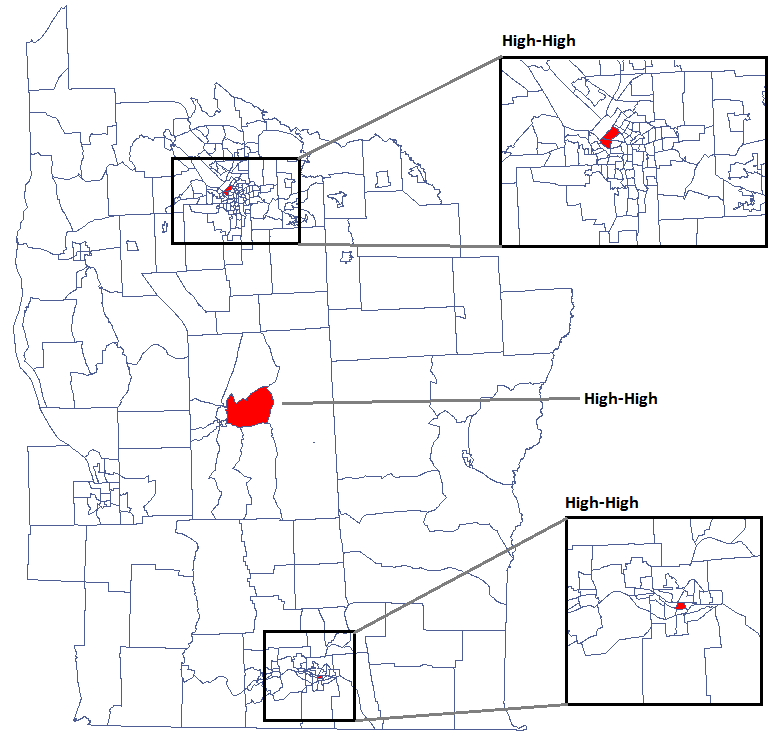
We were able to localize 3 clusters (6 census tracts in the analysis of the  coefficient and 4 tracts in the analysis of the
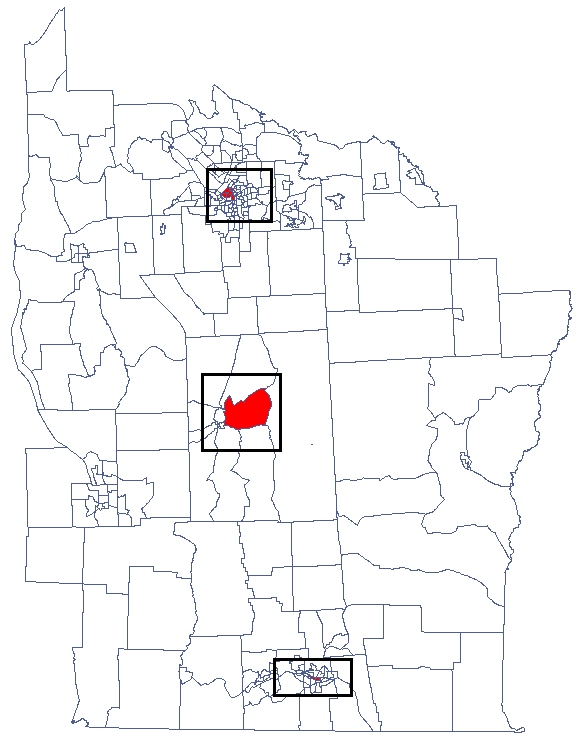
coefficient and 4 tracts in the analysis of the  coefficient) in which the prevalence of leukemia is significantly higher. They are the centers of clusters with high values of leukemia, marked in red on the map.
coefficient) in which the prevalence of leukemia is significantly higher. They are the centers of clusters with high values of leukemia, marked in red on the map.
The obtained results can be additionally illustrated by coloring the map so as to present the values of the local Getis and Ord's coefficient or the values of the test statistic, or the  values. One just has to copy the appropriate columns from the report and paste them into a datasheet. In this example we will use the values of the
values. One just has to copy the appropriate columns from the report and paste them into a datasheet. In this example we will use the values of the  test statistic for coloring. Having pasted it into an empty column of a datasheet, in the map manager we color the base map according to the values of that column, selecting the standard deviation with the coefficient 3 as a way of gradiating colors. Positive and high values of the
test statistic for coloring. Having pasted it into an empty column of a datasheet, in the map manager we color the base map according to the values of that column, selecting the standard deviation with the coefficient 3 as a way of gradiating colors. Positive and high values of the 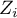 statistic point to a concentration of objects with high values, whereas negative and low values point to a concentration of objects with low values, and the values near zero point to a random spatial distribution of the studied variable (a map can be added with means and confidence intervals).
statistic point to a concentration of objects with high values, whereas negative and low values point to a concentration of objects with low values, and the values near zero point to a random spatial distribution of the studied variable (a map can be added with means and confidence intervals).
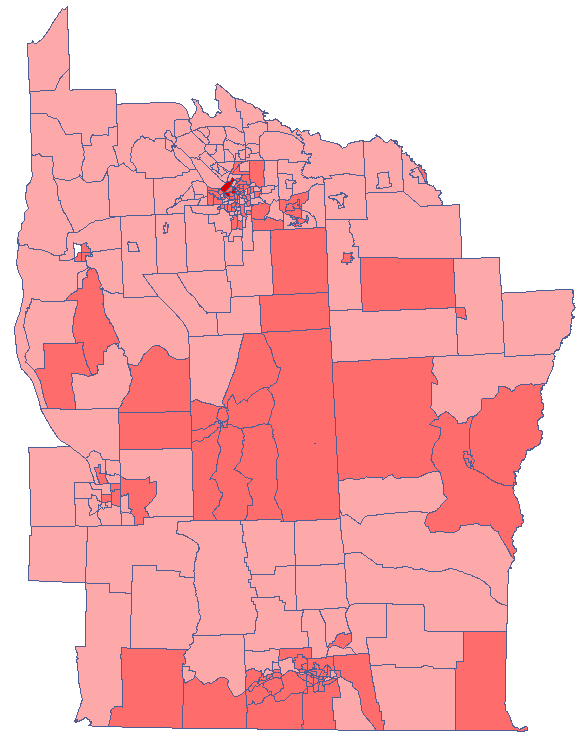
By analyzing the smoothed variable textsf{prev} we strengthen the clusterization effect. We obtain a similar result, i.e. 3 clusters (15 census tracts in the analysis of the  coefficient and 9 tracts in the analysis of the
coefficient and 9 tracts in the analysis of the  coefficient) which are cluster centers.
coefficient) which are cluster centers.
2022/02/09 12:56
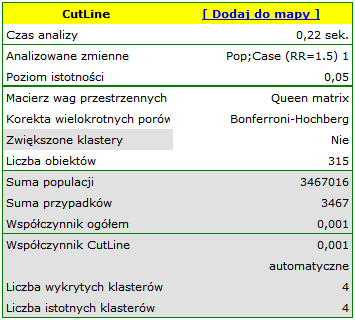
CutL
CutL method was developed to detect clusters that have significantly higher prevalence than that specified by the investigator (Więckowska2)). As a result, the program locates clusters, examines their statistical significance, and plots them on a map.
Note
Analysis is based on the commonly used Binomial test for equal proportions.
Analyses are conducted on aggregated data (polygons map). In each of the two columns of the data sheet, enter the population size and number of cases for EACH object – these are the data required for proper analysis.
The settings window of CutL statistic can be opened in Spatial analysis→Spatial statistics→CutL
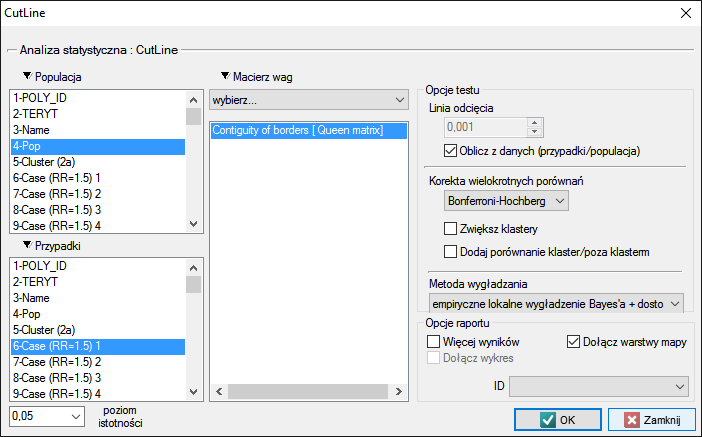
The analysis is based on data from the population size and number of cases, as well as the neighborhood matrix on the map.
Using the neighborhood matrix:
The Queen neighborhood matrix is the default chosen during the analysis. Other matrices may be used in this analysis, but this requires prior preparation and selection in the analysis window.
The cut-off line is the value above which statistically significant clusters can be detected and may be set in the analysis window. If the investigator does not specify this value, then it is set to the average prevalence calculated for the area under study.
Options
- Corrections for multiple comparisons – The following corrections for multiple comparisons may be used:
- Bonferroni-Hochberg
- Sidak-Hochberg
- Benjamini-Hochberg
- Compare cluster/outside
In addition, each cluster may be compared with the area outside of the cluster. The Binomial test for one proportion compares the prevalence within the cluster to the specified prevalence value, which is the prevalence outside of the cluster. Hypothesis testing is one-sided resulting from the higher prevalence inside the cluster than outside.
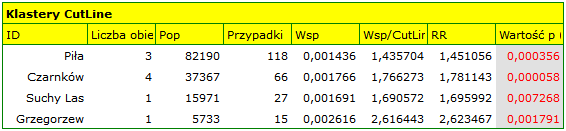
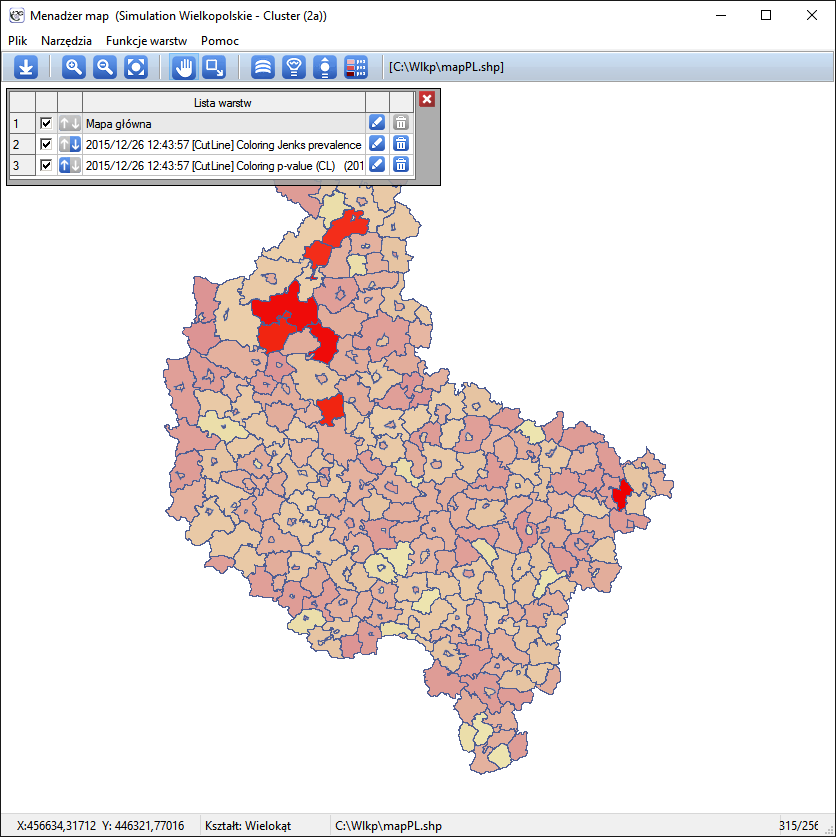
Results of Analysis
The results of the analysis are presented in the form of a report and map with superimposed layers.
Spatial-Temporal CutL
Using the CutL method, it is also possible to determine temporal-spatial clusters (Więckowska B. 2019 3)), i.e., clusters that do not persist for the entire time range under study, but only for a shorter period. Individual time layers are added to the datasheet by selecting Edit Timeline from the project tree, after indicating the appropriate map.
The spatio-temporal analysis window is obtained by selecting the menu Spatial analysis→Spatial statistics→CutL space-time.
2022/02/09 12:56
1)
Anselin L. (1995), Local Indicators of Spatial Association – LISA; Geographical Analysis, 27(2): 93–115
2)
Więckowska B., Marcinkowska J. (2017), CutL: an alternative to Kulldorff’s scan statistics for cluster detection with a specified cut-off level. Geospatial Health, 12(2): 556
3)
Więckowska B., Górna I., Trojanowski M., Pruciak A., Stawińska-Witoszyńska B. (2019), Searching for space-time clusters: The CutL method compared to Kulldorff's scan statistic 14(2
en/przestrzenpl/lokalpl.txt · ostatnio zmienione: 2022/02/16 13:44 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

