PQStat - Baza Wiedzy

Multicomparisons

Simultaneous testing of multiple hypotheses (the so-called family of hypotheses) carries the risk of increasing the error $\alpha$ , which is a major problem in the multicomparison field. When the error $\alpha$ increases, it means that the null hypothesis is too often rejected when it is true. That is, we too often indicate that there are differences, when in fact there are none. To protect against an increase in $\alpha$ one strategy is to adjust (decrease) the level of $\alpha$ or to adjust (increase) the p-values of the tests accordingly. The best known correction is the Bonferroni¹⁾ correction, which is also the most conservative. The Sidak (1967)²⁾ correction is somewhat more liberal. Both corrections have received several sequential improvements that increase their power. The program uses the step-up Holm's (1979)³⁾ procedure and the step-down Hochberg's (1988⁴⁾ procedure. The most powerful among the proposed corrections is Benjamini's (1995)⁵⁾ modified Hochberg's procedure, which does not directly control the error $\alpha$ but minimizes the expected percentage of false differences that occur among detected differences.

If we indicate by 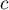$c$ the number of hypotheses being tested, then the adjustments to multicomparisons can be described as follows:

Bonferroni's correction

It involves multiplying each test probability by the total number of tests performed (or dividing the significance level by that number).

The p-value adjustment: $\begin{displaymath} p_{(Bonferroni,i)}=p_i\cdot c \end{displaymath}$

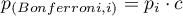
The significance level $\alpha$ adjustment:

$\begin{displaymath} \alpha_{(Bonferroni, i)}=\frac{\alpha_i}{c} \end{displaymath}$

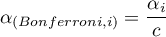
Sidak's correction

This correction is more powerful than the Bonferroni's correction (therefore it is becoming increasingly popular).

The p-value adjustment: $\begin{displaymath} p_{(Sidak, i)}=1-(1-p_i)^{c} \end{displaymath}$

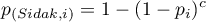
The significance level $\alpha$ adjustment:

$\begin{displaymath} \alpha_{(Sidak, i)}=1-(1-\alpha_i)^{1/c} \end{displaymath}$

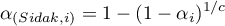
Bonferroni-Holm's correction

It involves using Holm's multi-step procedure for the Bonferroni's correction. The procedure begins with sorting consecutive values of 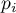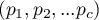$p_i$ $(p_1, p_2,...p_c)$ in an ascending order. Bonferroni's correction is then applied to each successive value of 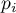$p_i$ (with a corresponding reduction in the number of hypotheses left to test). As a result, all hypotheses that are tested after the first statistically insignificant value of 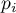$p_i$ are also insignificant.

The p-value adjustment: $\begin{displaymath} p_{(Bonferroni, i)}=p_i\cdot (c-i+1) \end{displaymath}$

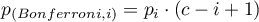
Sidak-Holm's correction

It involves using Holm's multi-step procedure for Sidak's correction. The procedure begins with sorting consecutive values of 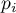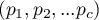$p_i$ $(p_1, p_2,...p_c)$ in an ascending order. The Sidak correction is then applied to each successive value of 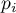$p_i$ (with a corresponding reduction in the number of hypotheses left to test). As a result, all hypotheses that are tested after the first statistically insignificant value of 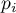$p_i$ are also insignificant.

The p-value adjustment: $\begin{displaymath} p_{(Sidak, i)}=1-(1-p_i)^{c-i+1} \end{displaymath}$

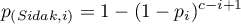
Bonferroni-Hochberg's correction

It involves the use of the multi-step Hochberg's procedure for the Bonferroni's correction. The procedure begins with sorting consecutive values of 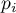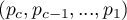$p_i$ $(p_c,p_{c-1},...,p_1)$ in a descending order. Bonferroni's correction is then applied to each successive value of 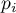$p_i$ (with a corresponding reduction in the number of hypotheses left to test). As a result, all hypotheses that are tested after the first statistically insignificant value of 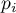$p_i$ are also insignificant.

The p-value adjustment: $\begin{displaymath} p_{(Bonferroni, i)}=p_i\cdot (c-i+1) \end{displaymath}$

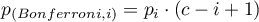
Sidak-Hochberg's correction

It involves the use of Hochberg's multi-step procedure for Sidak's correction. The procedure begins with sorting consecutive values of 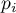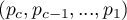$p_i$ $(p_c,p_{c-1},...,p_1)$ in a descending order. A Sidak correction is then applied to each successive value of 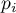$p_i$ (with a corresponding reduction in the number of hypotheses left to test). As a result, all hypotheses that are tested after the first statistically insignificant value of 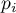$p_i$ are also insignificant.

Adjustment of the p-value: 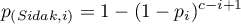$\begin{displaymath} p_{(Sidak, i)}=1-(1-p_i)^{c-i+1} \end{displaymath}$ </WRAP

Benjamini-Hochberg's correction

It involves the use of the multi-step Hochberg procedure for the Benjamini's correction which is a modified version of the Bonferroni's correction. The procedure starts with sorting consecutive values of 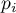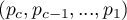$p_i$ $(p_c,p_{c-1},...,p_1)$ in a descending order. Benjamini's correction is then applied to each successive value of 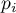$p_i$ (with a corresponding reduction in the number of hypotheses left to test). As a result, all hypotheses that are tested after the first statistically insignificant value of 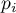$p_i$ are also insignificant.

Adjustment of the p-value: $\begin{displaymath} p_{(BH, i)}=p_i\frac{c}{i} \end{displaymath}$

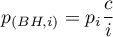
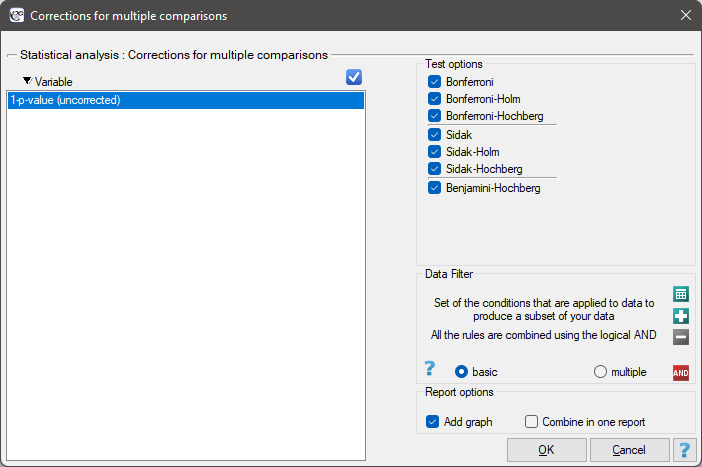
To perform a multicomparison correction, consecutive p-values are entered into one column of the datasheet.

The window with the multicomparison settings is opened via menu Statistics→Corrections for multiple comaprisons.

Note

A family of hypotheses can be defined in many ways. The most common are hypotheses within the POST-HOC procedure, i.e., the performing of multiple tests in a simultaneous comparison of several groups under study. Tests performed as part of a Hotelling-type analysis may also constitute such a family. Families of hypotheses are also found in many geographical analyses. Wherever multiple minor hypotheses are analyzed as part of an overall hypothesis, the multicomparisons correction may be applicable.

EXAMPLE cont. (jobSatisfaction.pqs file)

This study tested whether job satisfaction was the same for the four education categories. The family of hypotheses here was made up of hypotheses derived from pairwise comparisons of all groups. To compare all 4 groups, 6 pairs of comparisons were created. In each case, the null hypothesis was that there were no differences in satisfaction among the pairs analyzed. To take advantage of several proposed corrections of multicomparisons, the analysis was conducted using Dunn's uncorrected POST-HOC test.

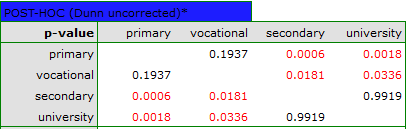
The resulting p-values were given as data for correction of multicomparisons yielding the following results:

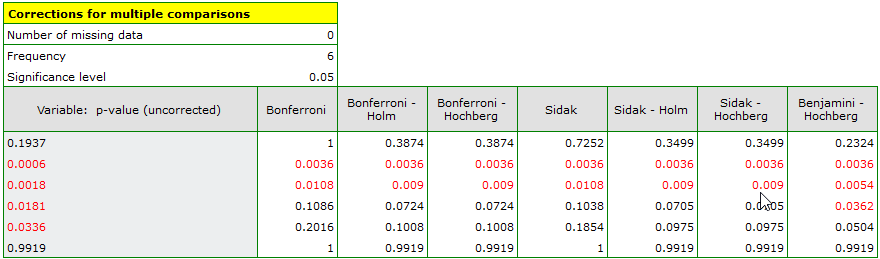
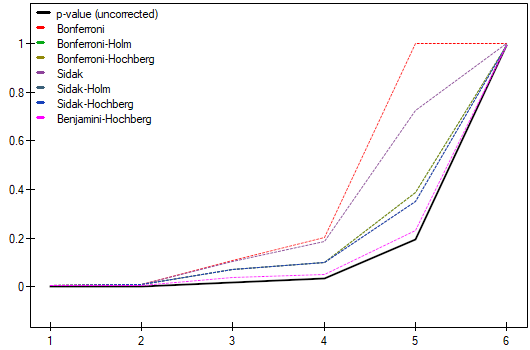
As a result, differences in job satisfaction were found to be statistically significant for two pairs of comparisons (elementary vs. secondary education and elementary vs. higher education). Using the Benjamini-Hochberg's correction only, differences could be found in three pairs.

OTHER EXAMPLES:

(sport.pqs file)

(hypertension.pqs file)

¹⁾

Abdi H. (2007), Bonferroni and Sidak corrections for multiple comparisons„, in N.J. Salkind (ed.): Encyclopedia of Measurement and Statistics. Thousand Oaks, CA: Sage

²⁾

Šidák Z. K. (1967), Rectangular Confidence Regions for the Means of Multivariate Normal Distributions. Journal of the American Statistical Association, 62 (318): 626–633

³⁾

Holm S. (1979), A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics 6, 65–70

⁴⁾

Hochberg Y. (1988), A sharper Bonferroni procedure for multiple tests of significance. Biometrika 75, 800–803

⁵⁾

Benjamini Y. and Hochberg Y. (1995), Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B 57, 289–300

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Multicomparisons

Narzędzia strony