Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:rozkladypl:ciaglepl
Continuous probability distributions
A density function is defined by:
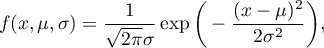
where:
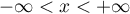 ,
,
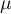 – an expected value of population (its measure is mean),
– an expected value of population (its measure is mean),
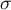 – standard deviation.
– standard deviation.
![LaTeX \psset{xunit=1.25cm,yunit=8cm}
\begin{pspicture}(-3.5,-.1)(4.2,0.9)
\psaxes[Dy=0.1]{->}(0,0)(-4.5,0)(5,0.9)
\uput[-90](5,0){x}\uput[0](0,0.85){y}
\psGauss[linecolor=red, linewidth=2pt, mue=0, sigma=1]{-4}{4}%
\rput(1.5,0.27){\textcolor{red}{$N(0,1)$}}
\psGauss[linecolor=blue, linestyle=dotted, mue=1, sigma=1]{-4}{4}%
\rput(2.6,0.25){\textcolor{blue}{$N(1,1)$}}
\psGauss[linecolor=green,linestyle=dashed, mue=0, sigma=0.5]{-4}{4}%
\rput(1.1,0.6){\textcolor{green}{$N(0,4)$}}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgdf0de30603271e67b32774a2ab3da458.png)
Normal distribution is a symmetrical distribution for a perpendicular line to axis of abscissae going through the points designating the mean, mode and median.
Normal distribution with a mean of 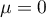 and
and  (
(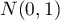 ), is so called a standardised normal distribution.
), is so called a standardised normal distribution.
A density function is defined by:
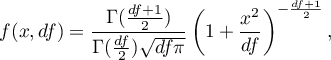
where:
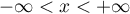 ,
,
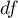 – degrees of freedom (sample size is decreased by the number of limitations in given calculations),
– degrees of freedom (sample size is decreased by the number of limitations in given calculations),
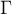 is a Gamma function.
is a Gamma function.
![LaTeX \psset{xunit=1.25cm,yunit=10cm}
\begin{pspicture}(-5,-0.1)(5,.5)
\psaxes[Dy=0.1]{->}(0,0)(-4.5,0)(5,0.5)
\uput[-90](5,0){x}\uput[0](0,0.45){y}
\psGauss[linecolor=red, linewidth=2pt, mue=0, sigma=1]{-4}{4}%
\rput(1.6,0.25){\textcolor{red}{$N(0,1)$}}
\psTDist[linecolor=blue,linestyle=dotted,nue=1]{-4}{4}
\rput(2.5,0.2){\textcolor{blue}{$T(df=1)$}}
\psTDist[linecolor=green,linestyle=dashed,nue=4]{-4}{4}
\rput(3,0.15){\textcolor{green}{$T(df=4)$}}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img87732e4f73e787194a3883f4b421d9a0.png)
Density function is defined by:
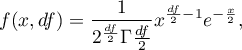
where:
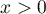 ,
,
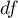 – degrees of freedom (sample size is decreased by the number of limitations in given calculations),
– degrees of freedom (sample size is decreased by the number of limitations in given calculations),
 is a Gamma function.
is a Gamma function.
{x}\uput[0](0,0.55){y}
\psChiIIDist[linewidth=1pt,linecolor=red, nue=1,]{0.01}{9}
\rput(1.8,0.4){\textcolor{red}{$\chi^2(df=1)$}}
\psChiIIDist[linewidth=1pt,linecolor=blue,linestyle=dotted, nue=5,]{0.01}{9}
\rput(4,0.2){\textcolor{blue}{$\chi^2(df=5)$}}
\psChiIIDist[linewidth=1pt,linecolor=green,linestyle=dashed, nue=10,]{0.01}{9}
\rput(8,0.15){\textcolor{green}{$\chi^2(df=10)$}}
\psaxes[Dy=0.1]{->}(0,0)(9.5,.6)
\end{pspicture*}](/lib/exe/fetch.php?media=wiki:latex:/img223648a7521a83822018c081beb401d1.png)
A density function is defined by:
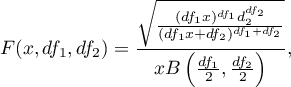
where:
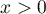 ,
,
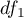 ,
, 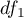 – degrees of freedom (it is assumed that if
– degrees of freedom (it is assumed that if  i
i  are independent with a
are independent with a  distribution with adequately
distribution with adequately 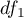 and
and 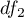 degrees of freedom, than
degrees of freedom, than 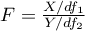 has a F Snedecor distribution
has a F Snedecor distribution 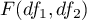 ),
),
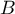 is a Beta function.
is a Beta function.
![LaTeX \psset{xunit=2cm,yunit=10cm,plotpoints=100}
\begin{pspicture*}(-0.5,-0.07)(5.5,0.8)
\psFDist[linecolor=green,linestyle=dashed]{0.1}{5}
\rput(1,0.05){\textcolor{green}{$F(df_1=1,df_2=1)$}}
\psFDist[linecolor=red,nue=3,mue=12]{0.01}{5}
\rput(4,0.15){\textcolor{red}{$F(df_1=3,df_2=12)$}}
\psFDist[linecolor=blue,linestyle=dotted,nue=12,mue=3]{0.01}{5}
\rput(2,0.4){\textcolor{blue}{$F(df_1=12,df_2=3)$}}
\psaxes[Dy=0.1]{->}(0,0)(5,0.75)
\end{pspicture*}](/lib/exe/fetch.php?media=wiki:latex:/img4153af385b1104035518012189a91db9.png)
en/statpqpl/rozkladypl/ciaglepl.txt · ostatnio zmienione: 2022/02/11 16:40 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

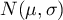 .
.