Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat Knowledge Base » PQStat - Statistic » Correlation » Parametric tests
Pasek boczny
en:statpqpl:korelpl:parpl
Spis treści
Parametric tests
The linear correlation coefficients
The Pearson product-moment correlation coefficient 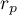 called also the Pearson's linear correlation coefficient (Pearson (1896,1900)) is used to decribe the strength of linear relations between 2 features. It may be calculated on an interval scale as long as there are no measurement outliers and the distribution of residuals or the distribution of the analyed features is a normal one.
called also the Pearson's linear correlation coefficient (Pearson (1896,1900)) is used to decribe the strength of linear relations between 2 features. It may be calculated on an interval scale as long as there are no measurement outliers and the distribution of residuals or the distribution of the analyed features is a normal one.
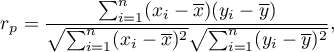
where:
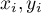 - the following values of the feature
- the following values of the feature  and
and  ,
,
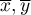 - means values of features:
- means values of features:  and
and  ,
,
 - sample size.
- sample size.
Note
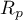 – the Pearson product-moment correlation coefficient in a population;
– the Pearson product-moment correlation coefficient in a population;
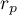 – the Pearson product-moment correlation coefficient in a sample.
– the Pearson product-moment correlation coefficient in a sample.
The value of 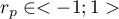 , and it should be interpreted the following way:
, and it should be interpreted the following way:
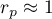 means a strong positive linear correlation – measurement points are closed to a straight line and when the independent variable increases, the dependent variable increases too;
means a strong positive linear correlation – measurement points are closed to a straight line and when the independent variable increases, the dependent variable increases too;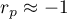 means a strong negative linear correlation – measurement points are closed to a straight line, but when the independent variable increases, the dependent variable decreases;
means a strong negative linear correlation – measurement points are closed to a straight line, but when the independent variable increases, the dependent variable decreases;- if the correlation coefficient is equal to the value or very closed to zero, there is no linear dependence between the analysed features (but there might exist another relation - a not linear one).
Graphic interpretation of 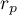 .
.
If one out of the 2 analysed features is constant (it does not matter if the other feature is changed), the features are not dependent from each other. In that situation 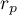 can not be calculated.
can not be calculated.
Note
You are not allowed to calculate the correlation coefficient if: there are outliers in a sample (they may make that the value and the sign of the coefficient would be completely wrong), if the sample is clearly heterogeneous, or if the analysed relation takes obviously the other shape than linear.
The coefficient of determination: 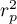 – reflects the percentage of a dependent variable a variability which is explained by variability of an independent variable.
– reflects the percentage of a dependent variable a variability which is explained by variability of an independent variable.
A created model shows a linear relationship:
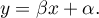
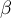 and
and  coefficients of linear regression equation can be calculated using formulas:
coefficients of linear regression equation can be calculated using formulas:
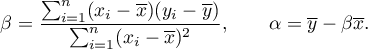
EXAMPLE cont. (age-height.pqs file)
2022/02/09 12:56
The Pearson correlation coefficient significance
The test of significance for Pearson product-moment correlation coefficient is used to verify the hypothesis determining the lack of linear correlation between an analysed features of a population and it is based on the Pearson's linear correlation coefficient calculated for the sample. The closer to 0 the value of coefficient 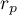 is, the weaker dependence joins the analysed features.
is, the weaker dependence joins the analysed features.
Basic assumptions:
- measurement on the interval scale,
- normality of distribution of residuals or an analysed features in a population.
Hypotheses:
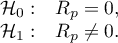
The test statistic is defined by:
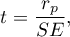
where 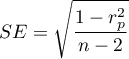 .
.
The value of the test statistic can not be calculated when 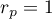 or
or 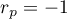 or when
or when 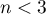 .
.
The test statistic has the t-Student distribution with 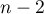 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

EXAMPLE cont. (age-height.pqs file)
2022/02/09 12:56
The slope coefficient significance
The test of significance for the coefficient of linear regression equation
This test is used to verify the hypothesis determining the lack of a linear dependence between an analysed features and is based on the slope coefficient (also called an effect), calculated for the sample. The closer to 0 the value of 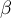 coefficient is, the weaker dependence presents the fitted line.
coefficient is, the weaker dependence presents the fitted line.
Basic assumptions:
- measurement on the interval scale,
- normality of distribution of residuals or an analysed features in a population.
Hypotheses:
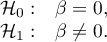
The test statistic is defined by:
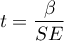
where:
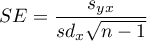 ,
,
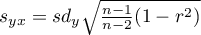 ,
,
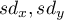 – standard deviation of the value of features:
– standard deviation of the value of features:  and
and  .
.
The value of the test statistic can not be calculated when 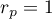 or
or 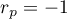 or when
or when 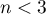 .
.
The test statistic has the t-Student distribution with 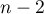 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Prediction
is used to predict the value of a one variable (mainly a dependent variable 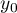 ) on the basis of a value of an another variable (mainly an independent variable
) on the basis of a value of an another variable (mainly an independent variable 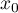 ). The accuracies of a calculated value are defined by prediction intervals calculated for it.
). The accuracies of a calculated value are defined by prediction intervals calculated for it.
- Interpolation is used to predict the value of a variable, which occurs inside the area for which the regression model was done. Interpolation is mainly a safe procedure - it is assumed only the continuity of the function of analysed variables.
- Extrapolation is used to predict the value of variable, which occurs outside the area for which the regression model was done. As opposed to interpolation, extrapolation is often risky and is performed only not far away from the area, where the regression model was created. Similarly to the interpolation, it is assumed the continuity of the function of analysed variables.
Analysis of model residuals - explanation in the Multiple Linear Regression module.
The settings window with the Pearson's linear correlation can be opened in Statistics menu→Parametric tests→linear correlation (r-Pearson) or in ''Wizard''.
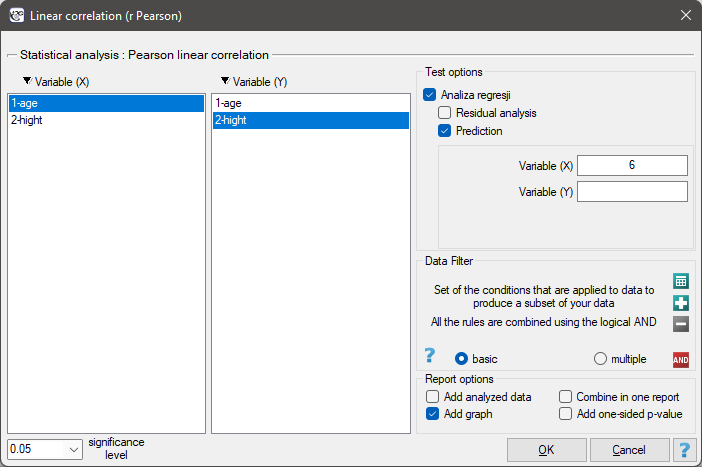
Among some students of a ballet school, the dependence between age and height was analysed. The sample consists of 16 children and the following results of these features (related to the children) were written down:
(age, height): (5, 128) (5, 129) (5, 135) (6, 132) (6, 137) (6, 140) (7, 148) (7, 150) (8, 135) (8, 142) (8, 151) (9, 138) (9, 153) (10, 159) (10, 160) (10, 162).}
Hypotheses:
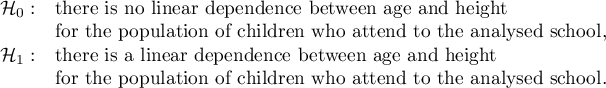
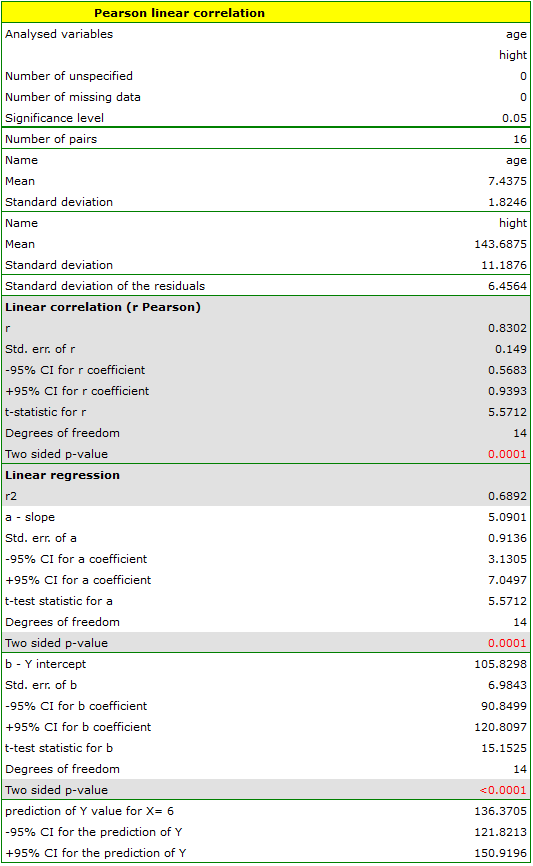
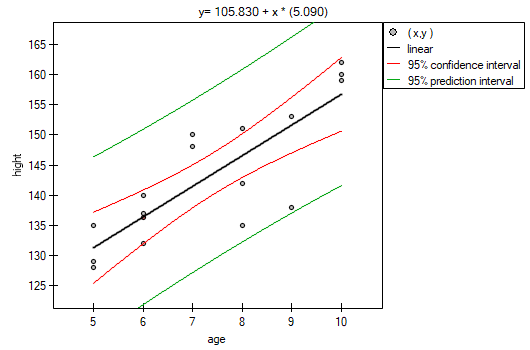
Comparing the  value < 0.0001 with the significance level
value < 0.0001 with the significance level  , we draw the conclusion, that there is a linear dependence between age and height in the population of children attening to the analysed school. This dependence is directly proportional, it means that the children grow up as they are getting older.
, we draw the conclusion, that there is a linear dependence between age and height in the population of children attening to the analysed school. This dependence is directly proportional, it means that the children grow up as they are getting older.
The Pearson product-moment correlation coefficient, so the strength of the linear relation between age and height counts to 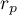 =0.83. Coefficient of determination
=0.83. Coefficient of determination 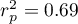 means that about 69\% variability of height is explained by the changing of age.
means that about 69\% variability of height is explained by the changing of age.
From the regression equation:
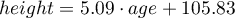 it is possible to calculate the predicted value for a child, for example: in the age of 6. The predicted height of such child is 136.37cm.
it is possible to calculate the predicted value for a child, for example: in the age of 6. The predicted height of such child is 136.37cm.
2022/02/09 12:56
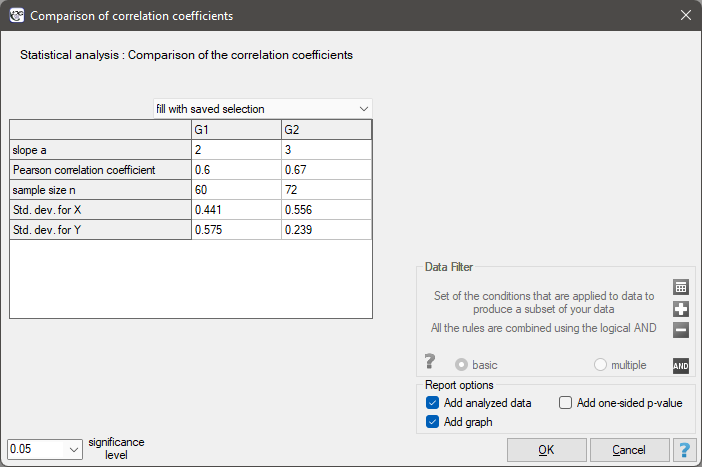
Comparison of correlation coefficients
The test for checking the equality of the Pearson product-moment correlation coefficients, which come from 2 independent populations
This test is used to verify the hypothesis determining the equality of 2 Pearson's linear correlation coefficients (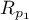 ,
, 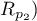 .
.
Basic assumptions:
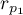 and
and 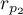 describe the strength of dependence of the same features:
describe the strength of dependence of the same features:  and
and  ,
,- sizes of both samples (
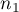 and
and 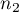 ) are known.
) are known.
Hypotheses:
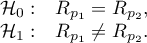
The test statistic is defined by:
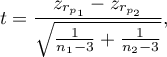
where:
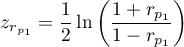 ,
,
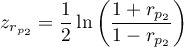 .
.
The test statistic has the t-Student distribution with 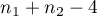 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Note
A comparison of the slope coefficients of the regression lines can be made in a similar way. </WRAP>
2022/02/09 12:56
Comparison of the slope of regression lines
The test for checking the equality of the coefficients of linear regression equation, which come from 2 independent populations
This test is used to verify the hypothesis determining the equality of 2 coefficients of the linear regression equation 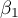 and
and 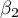 in analysed populations.
in analysed populations.
Basic assumptions:
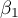 and
and 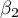 describe the strength of dependence of the same features:
describe the strength of dependence of the same features:  and
and  ,
,- both sample sizes (
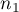 and
and 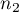 ) are known,
) are known,
Hypotheses:
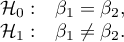
The test statistic is defined by:
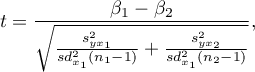
where:
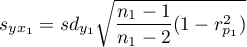 ,
,
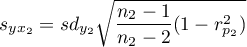 .
.
The test statistic has the t-Student distribution with 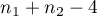 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the comparison of correlation coefficients can be opened in Statistics menu → Parametric tests → Comparison of correlation coefficients.
2022/02/09 12:56
en/statpqpl/korelpl/parpl.txt · ostatnio zmienione: 2022/02/13 18:28 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

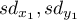 and
and 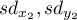 ) are known,
) are known,