PQStat - Baza Wiedzy

Measures of variability (dispersion)

Central tendency measures knowledge is not enough to fully describe a statistical data collection structure. The researched groups may have various variation levels of a feature you want to analyse. You need some formulas then, which enable you to calculate values of variability of the features.

Measures of variability are calculated only for an interval scale, because they are based on the distance between the points.

Range is formulated:

$\begin{displaymath} I=\max x_i - \min x_i \label{rozstep}, \end{displaymath}$

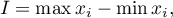
where 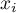$x_i$ are values of the analysed variable

$\begin{displaymath} IQR=\textrm{Interquartile range}=Q_3-Q_1 \label{rozstepkw}, \end{displaymath}$

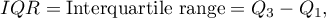
where 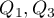$Q_1, Q_3$ are the lower and the upper quartile.

Ranges for a percentile scale (decile, centile) Ranges between percentiles are one of the dispersion measures. They define a percentage of all observations, which are located between the chosen percentiles.

Variance $-$ measures a degree of spread of the measurements around arithmetic mean

sample variance:

$\begin{displaymath} sd^2=\displaystyle{\frac{\sum_{i=1}^{n}(x_i-\overline{x})^2}{n-1}}, \label{wariancja} \end{displaymath}$

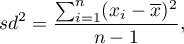
where 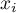$x_i$ are following values of variable and 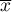$\overline{x}$ is an arithmetic mean of these values, n - sample size;

population variance:

$\begin{displaymath} \sigma^2=\displaystyle{\frac{\sum_{i=1}^{N}(x_i-\mu)^2}{N}}, \label{wariancja} \end{displaymath}$

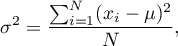
where 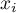$x_i$ are following values of variables and 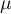$\mu$ is an arithmetic mean of these values, 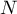$N$ - population size;

Variance is always positive, but it is not expressed in the same units as measuring results.

Standard deviation $-$ measures a degree of spread of the measurements around arithmetic mean.

sample standard deviation:

$\begin{displaymath} sd=\sqrt{sd^2}, \label{odch.standard} \end{displaymath}$

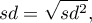
population standard deviation:

$\begin{displaymath} \sigma=\sqrt{\sigma^2}. \end{displaymath}$

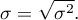
The higher standard deviation or a variance value is, the more diversed is the group in relation to an analysed feature.

Note The sample standard deviation is a kind of approximation (estimator) of the population standard deviation. The population standard deviation value is included in a range which contains the sample standard deviation. This range is called a **confidence interval ** for standard deviation.

Coefficient of variation

Coefficient of variation, just like standard deviation, enables you to estimate the homogeneity level of an analysed data collection. It is formulated as:

$\begin{displaymath} V=\frac{sd}{\overline{x}}100\% , \label{wspzmienn} \end{displaymath}$

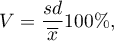
where 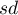$sd$ means standard deviation, 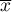$\overline{x}$ means arithmetic mean.

This is a unitless value. It enables you to compare a diversity of several different datasets of a one feature. And also, you are able to compare a diversity of several features (expressed in different units). It is assumed, if 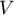$V$ coefficient does not exceed 10%, features indicate a statistically insignificant diversity.

Standard errors $-$ they are not measures of a measurement dispersion. They measure an accuracy level, you can define the population parameters value, having just the sample estimators.

Standard error of the mean is defined by:

$\begin{displaymath} SEM=\textrm{standard error of the mean}=\frac{sd}{\sqrt{n}} \label{sem}. \end{displaymath}$

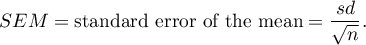
Note

On the basis of a sample estimator you can calculate a confidence interval for a population parameter.

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Measures of variability (dispersion)

Narzędzia strony