PQStat - Baza Wiedzy

More information about the variables in the model

* Standardized 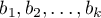$b_1,b_2,\ldots,b_k$ – In contrast to raw parameters (which are expressed in different units of measure, depending on the described variable, and are not directly comparable) the standardized estimates of the parameters of the model allow the comparison of the contribution of particular variables to the explanation of the variance of the dependent variable $Y$ .

Correlation matrix – contains information about the strength of the relation between particular variables, that is the Pearson's correlation coefficient 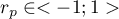$r_p \in <-1; 1>$ . The coefficient is used for the study of the corrrelation of each pair of variables, without taking into consideration the effect of the remaining variables in the model.
Covariance matrix – similarly to the correlation matrix it contains information about the linear relation among particular variables. That value is not standardized.
Partial correlation coefficient – falls within the range 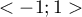$<-1; 1>$ and is the measure of correlation between the specific independent variable 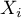$X_i$ (taking into account its correlation with the remaining variables in the model) and the dependent variable $Y$ (taking into account its correlation with the remaining variables in the model).

The square of that coefficient is the partial determination coefficient – it falls within the range 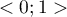$<0; 1>$ and defines the relation of only the variance of the given independent variable 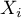$X_i$ with that variance of the dependent variable $Y$ which was not explained by other variables in the model.

The closer the value of those coefficients to 0, the more useless the information carried by the studied variable, which means the variable is redundant.

Semipartial correlation coefficient – falls within the range 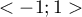$<-1; 1>$ and is the measure of correlation between the specific independent variable 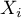$X_i$ (taking into account its correlation with the remaining variables in the model) and the dependent variable $Y$ (NOT taking into account its correlation with the remaining variables in the model).

The square of that coefficient is the semipartial determination coefficient – it falls within the range 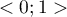$<0; 1>$ and defines the relation of only the variance of the given independent variable 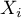$X_i$ with the complete variance of the dependent variable $Y$ .

The closer the value of those coefficients to 0, the more useless the information carried by the studied variable, which means the variable is redundants.

R-squared ( 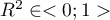$R^2 \in <0; 1>$ ) – it represents the percentage of variance of the given independent variable 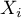$X_i$ , explained by the remaining independent variables. The closer to value 1 the stronger the linear relation of the studied variable with the remaining independent variables, which can mean that the variable is a redundant one.
Variance inflation factor ( 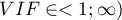$VIF \in <1; \infty )$ ) – determines how much the variance of the estimated regression coefficient is increased due to collinearity. The closer the value is to 1, the lower the collinearity and the smaller its effect on the coefficient variance. It is assumed that strong collinearity occurs when the coefficient VIF>5 \cite{sheather}. f the variance inflation factor is 5 ( 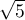$\sqrt{5}$ = 2.2), this means that the standard error for the coefficient of this variable is 2.2 times larger than if this variable had zero correlation with other variables $X_i$ .
Tolerance = 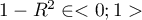$1-R^2 \in<0; 1>$ – it represents the percentage of variance of the given independent variable 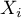$X_i$ , NOT explained by the remaining independent variables. The closer the value of tolerance is to 0 the stronger the linear relation of the studied variable with the remaining independent variables, which can mean that the variable is a redundant one.
A comparison of a full model with a model in which a given variable is removed

The comparison of the two model is made with by means of:

F test, in a situation in which one variable or more are removed from the model (see: the comparison of models),
t-test, when only one variable is removed from the model. It is the same test that is used for studying the significance of particular variables in the model.

In the case of removing only one variable the results of both tests are identical.

If the difference between the compared models is statistically significant (the value 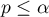$p \le \alpha$ ), the full model is significantly better than the reduced model. It means that the studied variable is not redundant, it has a significant effect on the given model and should not be removed from it.

Scatter plots

The charts allow a subjective evaluation of linearity of the relation among the variables and an identification of outliers. Additionally, scatter plots can be useful in an analysis of model residuals.

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

More information about the variables in the model

Narzędzia strony