PQStat - Baza Wiedzy

Więcej informacji o zmiennych w modelu

Standaryzowane 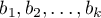$b_1,b_2,\ldots,b_k$ - w odróżnieniu od parametrów surowych (które w zależności od opisywanej zmiennej są wyrażone w różnych jednostkach miary i nie mogą być bezpośrednio porównywane) standaryzowane oceny parametrów modelu pozwalają porównywać wkład poszczególnych zmiennych w wyjaśnienie zmienności zmiennej zależnej $Y$ .

Macierz korelacji - zawiera informacje o sile związku pomiędzy poszczególnymi zmiennymi, czyli współczynnik korelacji Pearsona 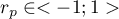$r_p \in <-1; 1>$ . Współczynnikiem tym badamy korelację dla każdej pary zmiennych, nie uwzględniając wpływu pozostałych zmiennych w modelu.

Macierz kowariancji - podobnie jak macierz korelacji, zawiera informacje o związku liniowym pomiędzy poszczególnymi zmiennymi. Przy czym wartość ta nie jest wystandaryzowana.

Współczynnik korelacji cząstkowej - należy do przedziału 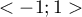$<-1; 1>$ i jest miarą korelacji pomiędzy konkretną zmienną niezależną 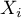$X_i$ (uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu) a zmienną zależną $Y$ (uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu).

Kwadrat tego współczynnika to współczynnik determinacji cząstkowej - należy do przedziału 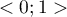$<0; 1>$ i oznacza stosunek wyłącznej zmienności danej zmiennej niezależnej 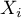$X_i$ do tej zmienności zmiennej zależnej $Y$ , która nie została wyjaśniona przez pozostałe zmienne w modelu.

Im wartość tych współczynników znajduje się bliżej 0, tym bardziej bezużyteczną informację niesie badana zmienna, czyli jest ona nadmiarowa.

Współczynnik korelacji semicząstkowej - należy do przedziału 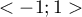$<-1; 1>$ i jest miarą korelacji pomiędzy konkretną zmienną niezależną 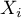$X_i$ (uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu) a zmienną zależną $Y$ (NIE uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu).

Kwadrat tego współczynnika to współczynnik determinacji semicząstkowej - należy do przedziału 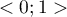$<0; 1>$ i oznacza stosunek wyłącznej zmienności danej zmiennej niezależnej 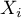$X_i$ do całkowitej zmienności zmiennej zależnej $Y$ .

Im wartość tych współczynników znajduje się bliżej zera, tym bardziej bezużyteczną informację niesie badana zmienna, czyli jest ona nadmiarowa.

R-kwadrat ( 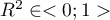$R^2 \in <0; 1>$ ) - wyraża on procent zmienności danej zmiennej niezależnej 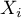$X_i$ tłumaczony przez pozostałe zmienne niezależne. Im bliżej wartości 1 tym silniej badana zmienna związana jest liniowo z pozostałymi zmiennymi niezależnymi, co może oznaczać, że jest ona zmienną nadmiarową.

współczynnik inflacji wariancji ( 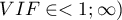$VIF \in <1; \infty)$ ) - określa jak bardzo wariancja szacowanego współczynnika regresji jest zwiększona z powodu współliniowości. Im bliżej wartości 1, tym mniejsza współliniowość i tym mniejszy jej wpływ na wariancję współczynnika. Przyjmuje się, że silna współliniowość występuje, gdy współczynnik VIF>5 ¹⁾. Jeśli współczynnik inflacji wariancji wynosi 5 ( 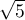$\sqrt{5}$ = 2.2), oznacza to, że błąd standardowy dla współczynnika tej zmiennej jest 2.2 razy większy niż w przypadku, gdyby ta zmienna miała zerową korelację z innymi zmiennymi $X_i$ .

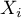Tolerancja = 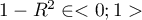$1-R^2 \in<0; 1>$ - wyraża on procent zmienności danej zmiennej niezależnej 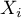$X_i$ NIE tłumaczony przez pozostałe zmienne niezależne. Im wartość tolerancji jest bliższa 0 tym silniej badana zmienna związana jest liniowo z pozostałymi zmiennymi niezależnymi, co może oznaczać, że jest ona zmienną nadmiarową.

Porównanie modelu pełnego z modelem po usunięciu danej zmiennej

Porównanie tych dwóch modeli dokonujemy:

testem F, w sytuacji gdy z modelu usuwamy jedną zmienną lub wiecej niż jedną zmienną (patrz porównywanie modeli),
testem t-Studenta, gdy z modelu usuwamy tylko jedną zmienną. Jest to ten sam test, którym badamy istotność poszczególnych zmiennych w modelu.

W przypadku usunięcia tylko jednej zmiennej wyniki obu tych testów są tożsame.

Jeśli różnica pomiędzy porównywanymi modelami jest istotna statystycznie (wartość 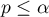$p \le \alpha$ ), wówczas model pełny jest istotnie lepszy niż model zredukowany. To oznacza, że badana zmienna nie jest nadmiarowa, wywiera ona istotny wpływ na dany model i nie powinna być z niego usuwana.

Wykresy rozrzutu

Wykresy te pozwalają dokonać subiektywnej oceny liniowości związku pomiędzy zmiennymi i zidentyfikować punkty odstające. Dodatkowo wykresami rozrzutu możemy posłużyć się w analizie reszt modelu.

¹⁾

Sheather S. J. (2009), A modern approach to regression with R. New York, NY: Springer

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Więcej informacji o zmiennych w modelu

Narzędzia strony