Spis treści

Wielokrotne porównania
- Wielokrotne porównania

Wielokrotne porównania

Jednoczesne testowanie wielu hipotez (tzw. rodziny hipotez) pociąga za sobą niebezpieczeństwo wzrostu błędu $\alpha$ , co stanowi główny problem w dziedzinie wielokrotnych porównań. Gdy błąd $\alpha$ wzrasta, to oznacza, że zbyt często odrzucamy hipotezę zerową, gdy jest ona prawdziwa. Czyli zbyt często wskazujemy na istnienie różnic, podczas, gdy w rzeczywistości różnice nie występują. Aby chronić przed wzrostem $\alpha$ jedną ze strategii jest poprawienie (zmniejszenie) poziomu $\alpha$ lub odpowiednie poprawienie (zwiększanie) wartości p testów. Najbardziej znaną korektą jest korekta Bonferroniego¹⁾, która jest jednocześnie najbardziej konserwatywna. Korekta Sidaka (1967)²⁾ jest nieco bardziej liberalna. Obie korekty doczekały się kilku sekwencyjnych ulepszeń zwiększających ich moc. W programie wykorzystano wstępującą krokową procedurę Holma (1979)³⁾ oraz zstępującą krokową procedurę Hochberga (1988)⁴⁾. Największą mocą wśród zaproponowanych korekt charakteryzuje się zmieniona przez Benjamini (1995)⁵⁾ procedura Hochberga, która nie kontroluje bezpośrednio błądu $\alpha$ ale minimalizuje oczekiwany odsetek fałszywych różnic które występują wśród różnic wykrytych.

Jeżeli liczbę testowanych hipotez oznaczymy przez $c$ , wówczas korekty dotyczące wielokrotnych porównań będzie można opisać następująco:

Korekta Bonferroniego

Polega na pomnożeniu każdego z prawdopodobieństw testowych przez całkowitą liczbę przeprowadzonych badań (lub podzieleniu poziomu istotności przez tą liczbę).

Korekta wartości $p$ :

$\begin{displaymath} p_{(Bonferroni,i)}=p_i\cdot c \end{displaymath}$

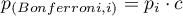
Korekta poziomu istotności $\alpha$ :

$\begin{displaymath} \alpha_{(Bonferroni, i)}=\frac{\alpha_i}{c} \end{displaymath}$

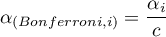
Korekta Sidaka

Korekta ta ma większą moc niż korekta Bonferroniego (dlatego jest coraz chętniej wykorzystywana).

Korekta wartości $p$ :

$\begin{displaymath} p_{(Sidak, i)}=1-(1-p_i)^{c} \end{displaymath}$

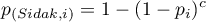
Korekta poziomu istotności $\alpha$ :

$\begin{displaymath} \alpha_{(Sidak, i)}=1-(1-\alpha_i)^{1/c} \end{displaymath}$

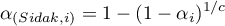
Korekta Bonferroniego-Holma

Polega na wykorzystaniu kilkukrokowej procedury Holma do poprawki Bonferroniego. Procedura ta rozpoczyna się od posortowania w sposób rosnący kolejnych wartości 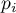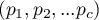$p_i$ $(p_1, p_2,...p_c)$ . Następnie zastosowana jest korekta Bonferroniego do każdej kolejnej wartości 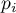$p_i$ (przy odpowiednim zmniejszeniu liczby hipotez jaka została do przetestowania). W rezultacie wszystkie hipotezy, które testowane są po pierwszej nieistotnej statystycznie wartości 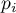$p_i$ , są również nieistotne.

Korekta wartości $p$ :

$\begin{displaymath} p_{(Bonferroni, i)}=p_i\cdot (c-i+1) \end{displaymath}$

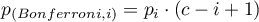
Korekta Sidaka-Holma

Polega na wykorzystaniu kilkukrokowej procedury Holma do poprawki Sidaka. Procedura ta rozpoczyna się od posortowania w sposób rosnący kolejnych wartości 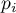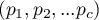$p_i$ $(p_1, p_2,...p_c)$ . Następnie zastosowana jest korekta Sidaka do każdej kolejnej wartości 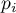$p_i$ (przy odpowiednim zmniejszeniu liczby hipotez jaka została do przetestowania). W rezultacie wszystkie hipotezy, które testowane są po pierwszej nieistotnej statystycznie wartości 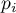$p_i$ , są również nieistotne.

Korekta wartości $p$ :

$\begin{displaymath} p_{(Sidak, i)}=1-(1-p_i)^{c-i+1} \end{displaymath}$

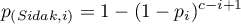
Korekta Bonferroniego-Hochberga

Polega na wykorzystaniu kilkukrokowej procedury Hochberga do poprawki Bonferroniego. Procedura ta rozpoczyna się od posortowania w sposób malejący kolejnych wartości 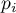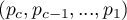$p_i$ $(p_c,p_{c-1},...,p_1)$ . Następnie zastosowana jest korekta Bonferroniego do każdej kolejnej wartości 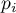$p_i$ (przy odpowiednim zmniejszeniu liczby hipotez jaka została do przetestowania). W rezultacie wszystkie hipotezy, które testowane są po pierwszej nieistotnej statystycznie wartości 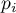$p_i$ , są również nieistotne.

Korekta wartości $p$ :

$\begin{displaymath} p_{(Bonferroni, i)}=p_i\cdot (c-i+1) \end{displaymath}$

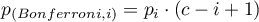
Korekta Sidaka-Hochberg

Polega na wykorzystaniu kilkukrokowej procedury Hochberga do poprawki Sidaka. Procedura ta rozpoczyna się od posortowania w sposób malejący kolejnych wartości 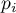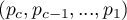$p_i$ $(p_c,p_{c-1},...,p_1)$ . Następnie zastosowana jest korekta Sidaka do każdej kolejnej wartości 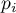$p_i$ (przy odpowiednim zmniejszeniu liczby hipotez jaka została do przetestowania). W rezultacie wszystkie hipotezy, które testowane są po pierwszej nieistotnej statystycznie wartości 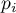$p_i$ , są również nieistotne.

Korekta wartości $p$ :

$\begin{displaymath} p_{(Sidak, i)}=1-(1-p_i)^{c-i+1} \end{displaymath}$

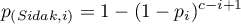
Korekta Benjamini-Hochberg

Polega na wykorzystaniu kilkukrokowej procedury Hochberga do poprawki Benjamini będącej zmodyfikowaną wersją poprawki Bonferroniego. Procedura ta rozpoczyna się od posortowania w sposób malejący kolejnych wartości 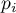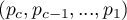$p_i$ $(p_c,p_{c-1},...,p_1)$ . Następnie zastosowana jest korekta Benjamini do każdej kolejnej wartości 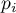$p_i$ (przy odpowiednim zmniejszeniu liczby hipotez jaka została do przetestowania). W rezultacie wszystkie hipotezy, które testowane są po pierwszej nieistotnej statystycznie wartości 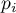$p_i$ , są również nieistotne.

Korekta wartości $p$ :

$\begin{displaymath} p_{(BH, i)}=p_i\frac{c}{i} \end{displaymath}$

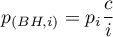
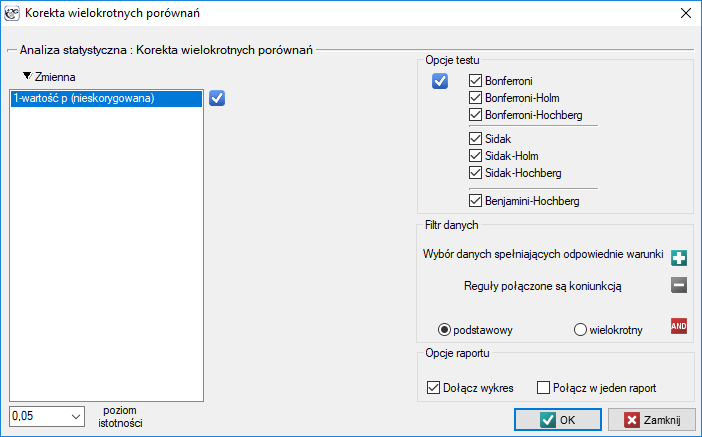
By wykonać korektę wielokrotnych porównań do jednej kolumny arkusza danych wprowadzamy kolejne wartości $p$ . Okno z ustawieniami opcji wielokrotnych porównań wywołujemy poprzez menu Statystyka→Korekta wielokrotnych porównań.

Uwaga!

Rodzina hipotez może być zdefiniowana na wiele sposobów. Najczęściej są to hipotezy w ramach procedury POST-HOC, czyli wykonywania wielu testów w ramach jednoczesnego porównania kilku badanych grup. Taką rodzinę stanowić mogą również testy wykonywane w ramach analizy typu Hotelling. Rodziny hipotez występują również w wielu analizach geograficznych. Wszędzie tam, gdzie w ramach ogólnej hipotezy analizujemy wiele pomniejszych hipotez korekta wielokrotnych porównań może mieć zastosowanie.

Przykład c.d. (plik satysfakcjaZpracy.pqs)

W badaniu tym sprawdzano, czy poziom satysfakcji z wykonywanej pracy jest taki sam dla czterech kategorii wykształcenia. Rodzinę hipotez tworzyły tu hipotezy wynikające z porównania wszystkich grup parami. By porównać wszystkie 4 grupy utworzono 6 par porównań. W każdym przypadku hipoteza zerowa dotyczyła braku różnic w poziomie satysfakcji w analizowanej parze. By wykorzystać kilka zaproponowanych korekt wielokrotnych porównań, analizę przeprowadzono przy pomocy nieskorygowanego testu POST-HOC Dunna.

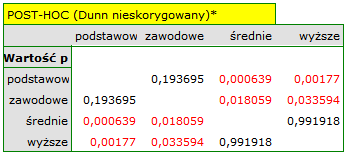
Uzyskane w ten sposób wartości p podano jako dane do korekty wielokrotnych porównań otrzymując następujące wyniki:

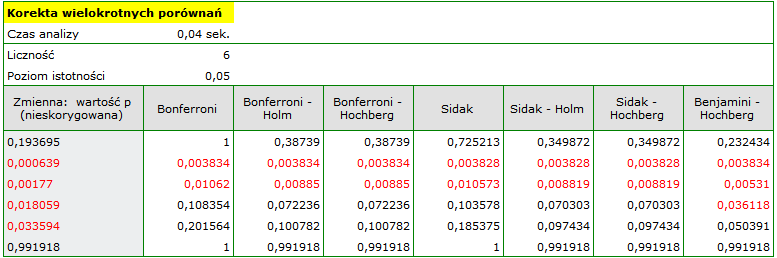
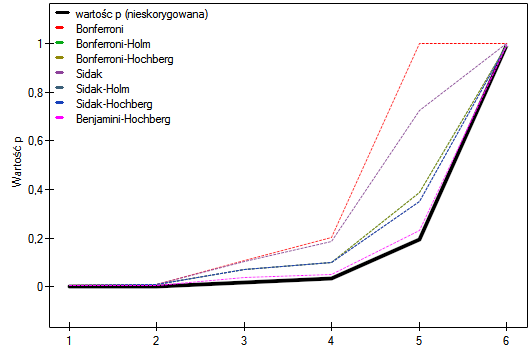
W rezultacie uznano za istotne statystycznie różnice dotyczące satysfakcji z pracy dla dwóch par porównań (wykształcenie podstawowe vs średnie i wykształcenie podstawowe vs wyższe). Tylko przy zastosowaniu korekty Benjamini-Hochberg różnice można zlokalizować w trzech parach porównań.

INNE PRZYKŁADY:

(plik sport.pqs)

(plik nadciśnienie.pqs)

2014/12/18 22:55 · admin

¹⁾

Abdi H. (2007), Bonferroni and Sidak corrections for multiple comparisons„, in N.J. Salkind (ed.): Encyclopedia of Measurement and Statistics. Thousand Oaks, CA: Sage

²⁾

Šidák Z. K. (1967), Rectangular Confidence Regions for the Means of Multivariate Normal Distributions. Journal of the American Statistical Association, 62 (318): 626–633

³⁾

Holm S. (1979), A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics 6, 65–70

⁴⁾

Hochberg Y. (1988), A sharper Bonferroni procedure for multiple tests of significance. Biometrika 75, 800–803

⁵⁾

Benjamini Y. and Hochberg Y. (1995), Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B 57, 289–300

PQStat - Baza Wiedzy

Pasek boczny

Spis treści

Wielokrotne porównania