Spis treści

Moc testu i liczność próby
- Niezbędna liczność próby

Moc testu i liczność próby

Do wyznaczania liczności próby możemy podejść na kilka wiele sposobów. Jedną z możliwości jest oszacowanie jak duża powinna być próba by w dobry sposób odzwierciedlać populację. Inną możliwością jest oszacowanie liczności próby do sytuacji stosowania konkretnych testów statystycznych. Wówczas oprócz niezbędnej liczności próby możemy być zainteresowani mocą tych testów. Pierwsze, i wydaje się łatwiejsze podejście, zaprezentowane jest w podrozdziale Niezbędna liczność próby, drugie w podrozdziale Moc i liczność dla testu.

Niezbędna liczność próby

Dla marginesu błędu proporcji i średniej

Ze względu na to, że badanie całej populacji najczęściej nie jest ani praktyczne ani możliwe, wybiera się jej podzbiór - próbę. Próba jest oczywiście odpowiednio mniej liczna niż populacja, ale powinna ją dobrze odzwierciedlać. Jednym z kluczowych aspektów przy planowaniu badania, obok losowości próby, jest założenie jej rozmiaru. Rozmiar powinien być tak dobrany, by wnioskowanie na temat populacji było prawdziwe.

Jeśli zainteresowani jesteśmy, by proporcje pewnych cech, lub ich wartości średnie, wyliczone dla próby odzwierciedlały proporcje lub wartości średnie w populacji z możliwie małym błędem, możemy odpowiednio oszacować niezbędną do tego celu liczność próby.

Liczność próby dla oszacowania proporcji populacji

Zakładając możliwość popełnienia błędu szacunku wielkości 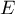$E$ , możemy wyznaczyć niezbędną liczność próby 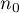$n_0$ - dla nieznanej wielkości populacji lub 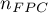$n_{FPC}$ - dla znanej wielkości populacji.

$\begin{displaymath} n_0=\frac{Z^2p(1-p)}{E^2} \end{displaymath}$

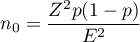
gdzie:

$p$ – podana przez badacza oczekiwana proporcja w populacji, przy czym - jeśli wielkość ta nie jest znana, oszacowana niezbędna liczność będzie tak zwiększona, by była wystarczająca dla każdej możliwej proporcji, zatem wykorzystana zostanie wartość $p=0.5$ .

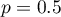W przypadku, gdy znamy liczność populacji (a w szczególności - gdy liczność jest relatywnie mała w stosunku do 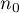$n_0$ , tzn. gdy 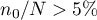$n_0/N>5\%$ ) powinniśmy stosować tzw. korektę skończonej populacji ( $FPC$ ) (Lenth (2001)¹⁾, Armitage i Colton (2009)²⁾) daną wzorem:

$\begin{displaymath} n_{FPC}=\frac{n_0N}{n_0+(N-1)} \end{displaymath}$

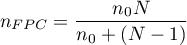
Liczność próby dla oszacowania średniej populacji

Zakładając możliwość popełnienia błędu szacunku wielkości 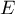$E$ , możemy wyznaczyć niezbędną liczność próby 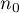$n_0$ - dla nieznanej wielkości populacji lub 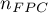$n_{FPC}$ - dla znanej wielkości populacji.

$\begin{displaymath} n_0=\frac{Z^2\sigma^2}{E^2} \end{displaymath}$

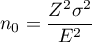
gdzie:

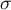$\sigma$ – odchylenie standardowe populacji - znane na podstawie wcześniejszych badań.

W przypadku, gdy znamy liczność populacji (a w szczególności - gdy liczność jest relatywnie mała w stosunku do 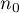$n_0$ , tzn. gdy 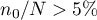$n_0/N>5\%$ ) powinniśmy stosować tzw. korektę skończonej populacji ( 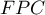$FPC$ ) daną wzorem:

$\begin{displaymath} n_{FPC}=\frac{n_0N}{n_0+(N-1)} \end{displaymath}$

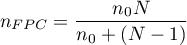
Okno z ustawieniami opcji Niezbędnej liczności próby wywołujemy poprzez menu Statystyki zaawansowane→Moc testu i liczność próby→Niezbędna liczność próby.

Przykład (Szacowanie proporcji)

Populacja: Uprawnieni do głosowania na prezydenta Polski.

Zainteresowani jesteśmy poparciem dla poszczególnych kandydatów.

Ile osób wybrać by uzyskany odsetek obarczony był błędem co najwyżej 2%?

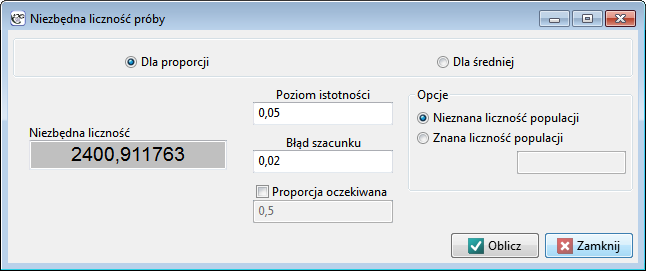
Przy próbie przynajmniej 2401 elementowej będziemy mieć 95% pewności, że błąd poparcia dla wybranego kandydata na prezydenta nie przekracza 2%. Oznacza to, że w 95% eksperymentów polegających na pobieraniu losowej, 2401 elementowej próby z populacji, błąd szacunku poparcia dla danego kandydata nie przekroczy 2%, ale w 5% takich eksperymentów może on być większy niż 2%.

Przy wyborze wielkości dopuszczanego błędu należy zwrócić uwagę na to, czy nie zachodzi taka sytuacja, iż w wyborach biorą udział również kandydaci o niewielkim poparciu (na granicy założonego błędu szacunku). Jeśli tak jest, warto zmniejszyć wartość zakładanego błędu - konsekwencją zmniejszenia błędu będzie wówczas wzrost niezbędnej liczności próby.

Przykład (Szacowanie wartości średniej)

Populacja: Osoby chorujące na nadciśnienie w Polsce w latach 2005-2010, w wieku 20-40 lat.

Zainteresowani jesteśmy średnią masą ciała tych ludzi.

Ile osób wybrać by średnia masa obarczona była błędem co najwyżej 3kg? Wiemy, że populacyjne odchylenie standardowe masy ciała tych osób wynosi 18kg.

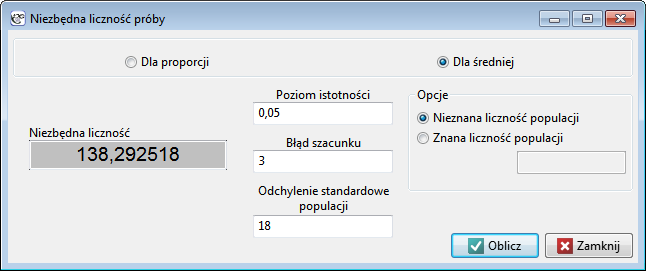
By mieć 95% pewności, że w marginesie błędu ( $\pm$ 3kg) zbudowanym wokół średniej z naszej próby znajduje się średnia populacyjna potrzebujemy zebrać przynajmniej 139 osób.

2015/05/04 13:16 · admin

¹⁾

Lenth, R. V., (2001), Some Practical Guidelines for Effective Sample Size Determination. The American Statistician, 55(3), 187-193

²⁾

Armitage P., Colton T., (2009), Encyclopedia of Biostatistcs. John Wiley and Sons.

PQStat - Baza Wiedzy

Pasek boczny

Spis treści

Moc testu i liczność próby

Niezbędna liczność próby

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Spis treści

Moc testu i liczność próby

Niezbędna liczność próby

Narzędzia strony