Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Moc testu i liczność próby » Moc i liczność dla testu
Pasek boczny
statpqpl:niezbliczpl:moclicznpl
Spis treści
Moc i liczność dla testu
 Okno z ustawieniami opcji mocy testu i niezbędnej liczności próby dla tego testu wywołujemy poprzez menu
Okno z ustawieniami opcji mocy testu i niezbędnej liczności próby dla tego testu wywołujemy poprzez menu Statystyka zaawansowana→Moc testu i liczność próby→Moc i liczność dla testu.
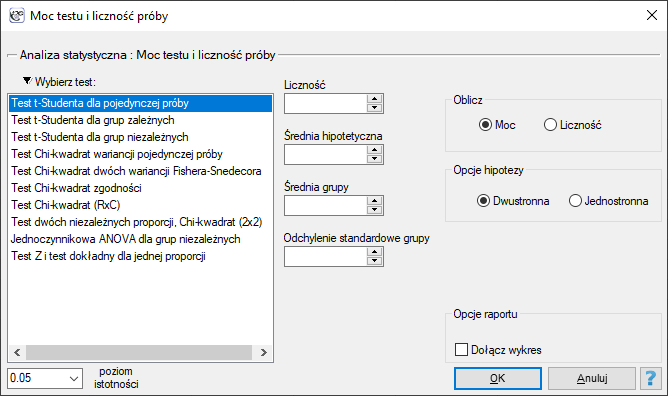
Analiza mocy jest bezpośrednio związana z testowaniem hipotez, a wiec z konkretnymi testami statystycznymi. Testy różnią się swoją mocą. Jedne testy są silniejsze, inne słabsze. W związku z tym faktem, jeśli do rozwiązania danego problemu statystycznego mamy do dyspozycji kilka testów, lepiej jest wybrać ten test, który ma większą moc. Taki test jest silniejszy, więc łatwiej odrzuci hipotezę zerową, a zatem łatwiej będzie nam udowodnić hipotezę alternatywną - co jest przecież celem badacza.
Moc testu statystycznego jest to zdolność testu do wykrywania różnic, związków, zgodności i wszelkiego rodzaju zależności, które opisujemy w hipotezie alternatywnej. Językiem fachowym mocą testu nazywamy prawdopodobieństwo przyjęcia hipotezy alternatywnej gdy ona jest w rzeczywistości prawdziwa.
Sprawdzenie mocy testu może być wykonywane a priori tzn. przed zebraniem danych do badania właściwego, ale często to recenzenci prac lub my sami już w trakcie analiz czyli a'posteriori tzn. po zebraniu właściwej próby jesteśmy zainteresowani jaka jest moc analiz, które wykonujemy. Jeśli moc testu jest mała, wówczas uzyskane wyniki mogą być niejednoznaczne, jeśli duża - możemy się spodziewać, że w przyszłości trudno będzie innym badaczom uzyskać wyniki odmienne tzn. podważyć nasze rezultaty. Na przykład gdy wykazujemy przy pomocy testu o mocy 80%, że dwie grupy studentów różnią się od siebie istotnie statystycznie pod względem liczby poprawnie rozwiązanych zadań, oznacza to, że gdy inni badacze będą powtarzać ten eksperyment w takich samych warunkach jak my, to w 80% losowych prób takiej wielkości jak nasza, stosując ten sam test i przyjmując ten sam poziom istotności, również udowodnią hipotezę alternatywną.
Moc testu określana jest wzorem:
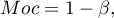
gdzie:
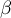 - błąd II rodzaju, czyli prawdopodobieństwo przyjęcia hipotezy zerowej gdy jest ona fałszywa.
- błąd II rodzaju, czyli prawdopodobieństwo przyjęcia hipotezy zerowej gdy jest ona fałszywa.
Moc testu związana jest bezpośrednio z licznością próby  - czym liczniejsza próba, tym większa moc, tzn. czym więcej zbierzemy studentów by przeprowadzić badanie, tym łatwiej będzie przekonać, że wykryte różnice między grupami nie są dziełem przypadku, ale rzeczywiście występują między populacjami. Stąd w tym samym podejściu badacz może być zainteresowany wyznaczeniem niezbędnej liczności próby dla danego testu statystycznego przy zachowaniu jego mocy na zadanym poziomie.
W programie PQStat możemy obliczyć moc testu zadając liczność próby, lub obliczyć liczność próby zadając moc testu jaką chcemy osiągnąć. Niestety zarówno moc testu jak też liczność próby, oprócz tego że są związane z sobą wzajemnie, zależą również od innych dodatkowych informacji dotyczących zebranej próby, które należy ustalić, są to:
- czym liczniejsza próba, tym większa moc, tzn. czym więcej zbierzemy studentów by przeprowadzić badanie, tym łatwiej będzie przekonać, że wykryte różnice między grupami nie są dziełem przypadku, ale rzeczywiście występują między populacjami. Stąd w tym samym podejściu badacz może być zainteresowany wyznaczeniem niezbędnej liczności próby dla danego testu statystycznego przy zachowaniu jego mocy na zadanym poziomie.
W programie PQStat możemy obliczyć moc testu zadając liczność próby, lub obliczyć liczność próby zadając moc testu jaką chcemy osiągnąć. Niestety zarówno moc testu jak też liczność próby, oprócz tego że są związane z sobą wzajemnie, zależą również od innych dodatkowych informacji dotyczących zebranej próby, które należy ustalić, są to:
- Wielkość efektu
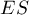 (ang. effect size) jaki uznajemy za ważny. Im większy efekt, tym większa moc i tym mniejsza próba jest potrzebna by tę moc uzyskać. Na przykład uzyskując różnicę pięciu poprawnie rozwiązanych zadań łatwiej będzie przekonać, że w rzeczywistości grupy różnią się (będziemy mieli większą moc argumentu) niż wtedy, gdy próbowalibyśmy przekonać o rzeczywistej przewadze jednej z grup studenckich podając, że różnią się zaledwie jednym poprawnie rozwiązanym zadaniem.
(ang. effect size) jaki uznajemy za ważny. Im większy efekt, tym większa moc i tym mniejsza próba jest potrzebna by tę moc uzyskać. Na przykład uzyskując różnicę pięciu poprawnie rozwiązanych zadań łatwiej będzie przekonać, że w rzeczywistości grupy różnią się (będziemy mieli większą moc argumentu) niż wtedy, gdy próbowalibyśmy przekonać o rzeczywistej przewadze jednej z grup studenckich podając, że różnią się zaledwie jednym poprawnie rozwiązanym zadaniem.
Do wyznaczenia mocy lub niezbędnej liczności zwykle badany efekt musi zostać zestandaryzowany, dlatego w wielu sytuacjach konieczne jest podanie dodatkowych informacji np. odchylenia standardowego, współczynnika korelacji i innych współczynników, które pozwalają zestandaryzować taki efekt.
- Poziomem istotności statystycznej
 (błąd I rodzaju) - im większy poziom istotności, tym większa moc. Niestety poziom istotności, to ta część analizy, na którą mamy tylko pozorny wpływ, to znaczy niewiele jest sytuacji kiedy można ją zmieniać, a jeśli już dozwolona jest zmiana, to polegająca na zmniejszeniu
(błąd I rodzaju) - im większy poziom istotności, tym większa moc. Niestety poziom istotności, to ta część analizy, na którą mamy tylko pozorny wpływ, to znaczy niewiele jest sytuacji kiedy można ją zmieniać, a jeśli już dozwolona jest zmiana, to polegająca na zmniejszeniu  (patrz Wielokrotne porównania). Zwykle przyjmujemy
(patrz Wielokrotne porównania). Zwykle przyjmujemy 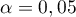 .
.
- Kierunek hipotezy tzn. hipoteza dwustronna (równość w hipotezie zerowej) lub jednostronna (znak < lub > w hipotezie zerowej). Hipoteza jednostronna daje większą moc, ale jest znacznie rzadziej wybierana, gdyż w rzeczywistych sytuacjach stosując test statystyczny rzadko zakładamy, że np. studenci z pierwszej populacji nie mają szansy pokonać studentów z drugiej populacji, często natomiast na stracie dajemy równe szanse obu grupom.
Przed przystąpieniem do wyznaczania mocy testu należy znać zasady jego stosowania, rozumieć jego hipotezy i umieć określić wielkość efektu, a jeśli dysponujemy danymi z badania np. pilotażowego, to również wykonać ten test.
Test t-Studenta dla pojedynczej próby
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu t-Studenta dla pojedynczej próby warto zapoznać się z zasadami jego stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy:

Zadana wielkość efektu, to w tym przypadku wielkość różnicy między zadaną średnią populacji badanej a hipotetyczną wartością średnią.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o niecentralny rozkład t-Studenta.
Przykład
Chcemy sprawdzić (na poziomie istotności 0.05) czy czas oczekiwania na dostarczenie przesyłki przez pewną firmę kurierską to przeciętnie 3 dni (tzn. 72 godziny).
- Badanie a priori - planujemy przeprowadzić badanie, ale nie zebraliśmy jeszcze danych.
Moc testu jaką chcemy uzyskać ustalamy na poziomie 80%.
Odchylenie standardowe, które podamy powinno odzwierciedlać różnice w czasie dostarczenia przesyłki jakie spodziewamy się uzyskać w planowanym badaniu - my zakładamy (na bazie doświadczeń pracowników tej firmy), że wyniesie ono 1 dzień (24 h).
a) Jaka będzie niezbędna liczność próby, gdy założymy, że wielkość efektu przy którym chcielibyśmy uzyskać istotność statystyczną wynosi 12 godzin (0.5 dnia)?
b) Jaka będzie niezbędna liczność próby, gdy założymy, że wielkość efektu przy którym chcielibyśmy uzyskać istotność statystyczną wynosi 6 godzin (0.25 dnia)?
Odp a) Wiemy, że zakres od 2.5 do 3.5 dnia mieści się w granicach dopuszczonego błędu. Jako średnią hipotetyczną podajemy więc 3 dni a jako średnią grupy badanej 2.5 dnia (lub 3.5 dnia).
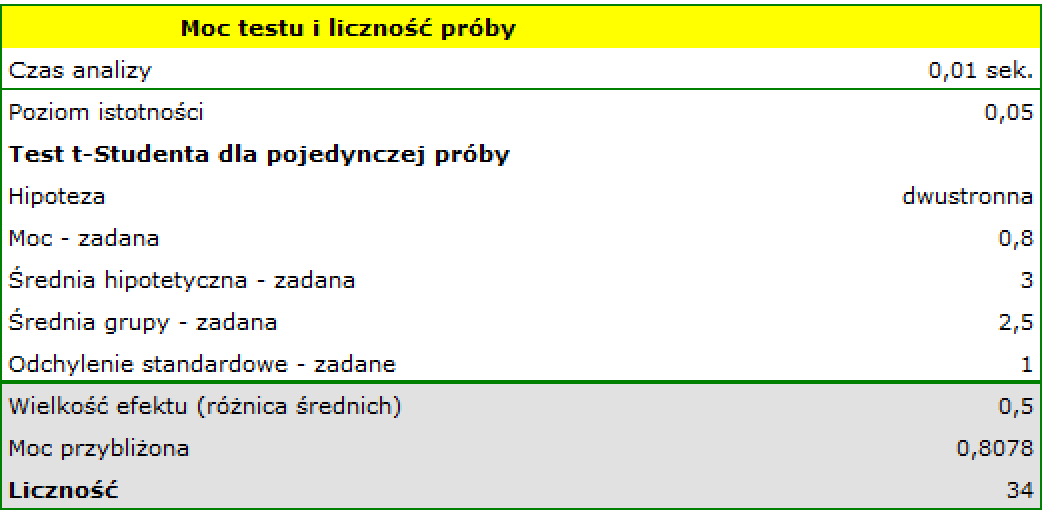
Uzyskana niezbędna liczność, która pozwoli na udowodnienie, że efekt przekraczający 12 godzin jest istotny statystycznie wynosi 34 przesyłki.
Odp b) Wiemy, że zakres od 2.75 do 3.25 dnia mieści się w granicach dopuszczonego błędu. Jako średnią hipotetyczną podajemy więc 3 dni a jako średnią grupy badanej 2.75 dnia (lub 3.25 dnia).
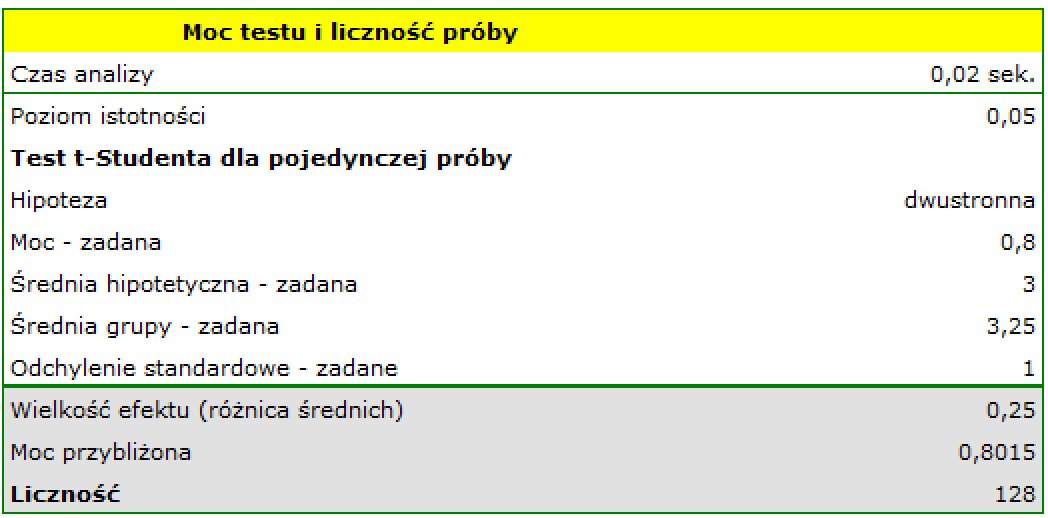
Uzyskana niezbędna liczność, która pozwoli na udowodnienie, że efekt przekraczający 6 godzin jest istotny statystycznie wynosi 128 przesyłek.
- Badanie a posteriori - zebraliśmy dane do badania - nasza próba zawiera 22 przesyłki (dane w pliku kurier.pqs).
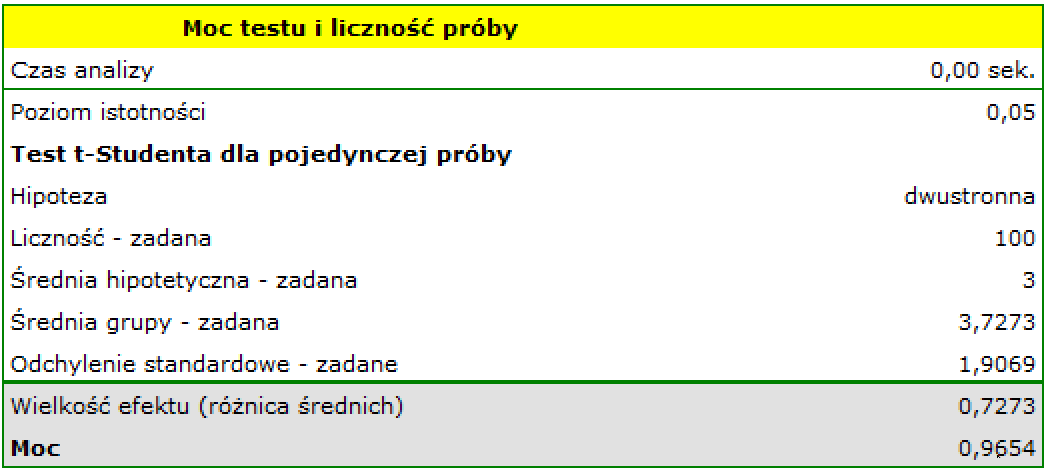
Na podstawie zebranych danych wyznaczamy średnią liczbę dni oczekiwania na dostarczenie przesyłki i odchylenie standardowe grupy. W naszym przypadku wynoszą one średnia=3.727273, odchylenie=1.906925.
a) Jaka jest moc przeprowadzonej analizy?
b) Jak wyglądałaby moc, gdybyśmy zwiększali liczność próby do 100 elementów, pozostawiając jednocześnie niezmienione pozostałe założenia?
Odp a) Moc przeprowadzonej analizy wynosi zaledwie 0.400302.
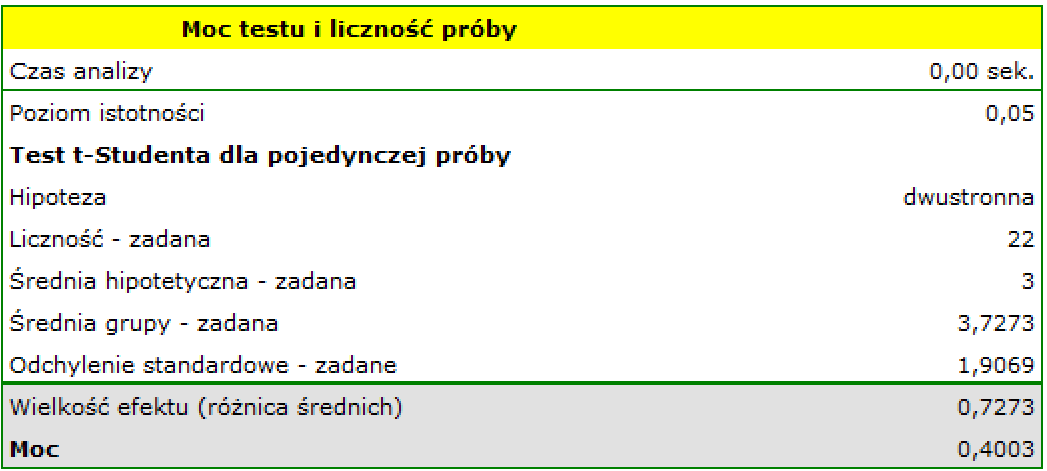
Wiemy stąd, że wiele losowych prób o liczności równej 22 (około 60% takich prób) nie będzie prowadziło do potwierdzenia hipotezy alternatywnej.
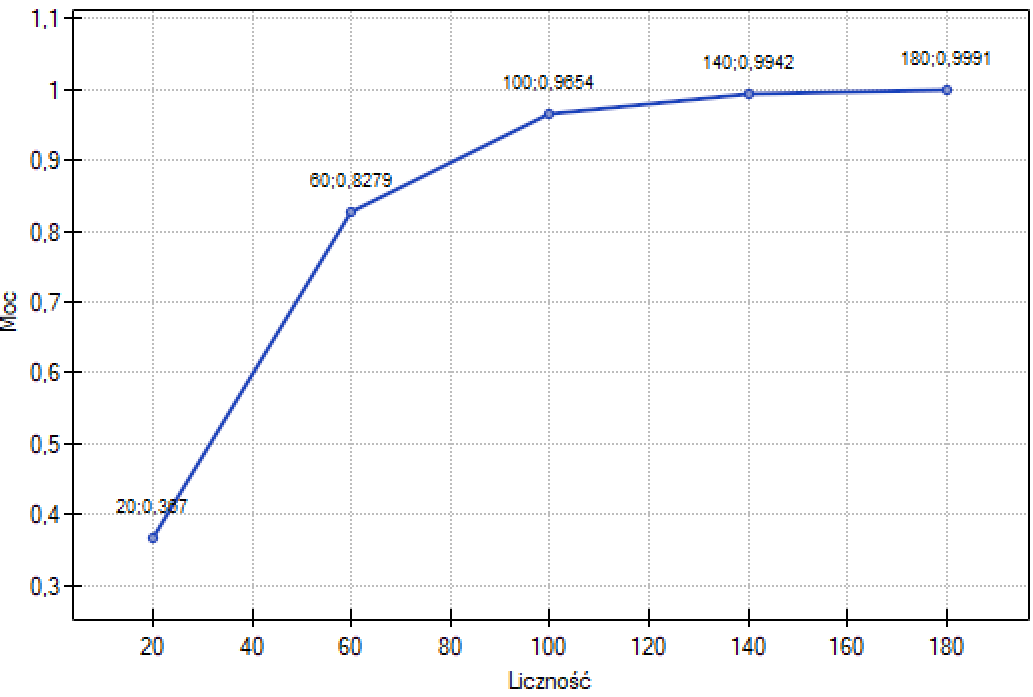
Odp b) Moc przeprowadzonej przez nas analizy wzrośnie do 0.965364 gdy jej liczność wzrośnie do 100 elementów, a założenia analizy się nie zmienią.
Jak będzie się zmieniała moc analizy przy zmieniającej się liczności próby i niezmienionych pozostałych założeniach możemy zobaczyć na wykresie.
Test t-Studenta dla grup zależnych
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu t-Studenta dla grup zależnych warto zapoznać się z zasadami jego stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy:

Zadana wielkość efektu, to w tym przypadku wielkość różnicy między średnimi jaką spodziewamy się uzyskać w populacji.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o niecentralny rozkład t-Studenta.
Przykład
Chcemy sprawdzić (na poziomie istotności 0.05) czy lecznie zaburzeń odżywiania w pewnej klinice przynosi istotne zmniejszenie masy ciała już po 30 dniach stosowania nowego rodzaju diety. Przy czym za istotną zmianę masy ciała uznajemy zmianę wskaźnika BMI o pół jednostki. Jak dużą próbę należy zebrać, by różnica tej wielkości była istotna statystycznie w teście t-Studenta dla grup zależnych?
Ponieważ nie dysponujemy danymi z badania pilotażowego, podstawowe dane do obliczeń podamy na bazie doświadczeń i przypuszczeń pracowników kliniki.
Zakładamy, że przeciętna wartość BMI osoby leczonej to 35 - taką wartość wpisujemy w polu dotyczącym pierwszej średniej. Ponieważ zmiana BMI o mniej niż połowę jednostki jest nieistotna klinicznie, dopiero spadek poniżej wartości 34.5 (lub wzrost powyżej wartości 35.5) będzie uznawany za istotny. Jako drugą średnią podajemy więc wartość 34.5 (lub 35.5). Przypuszczamy, że odchylnie standardowe różnicy (BMI przed i BMI po) może być dość duże, gdyż zwykle w grupie znajdą się osoby zdyscyplinowane by przestrzegać diety i takie, które mimo wszystko pozwalają sobie na dodatkowe przekąski między posiłkami. Dlatego wielkość odchylenia ustalamy na 2.5. Moc analizy, jaką chcemy uzyskać to 80%.
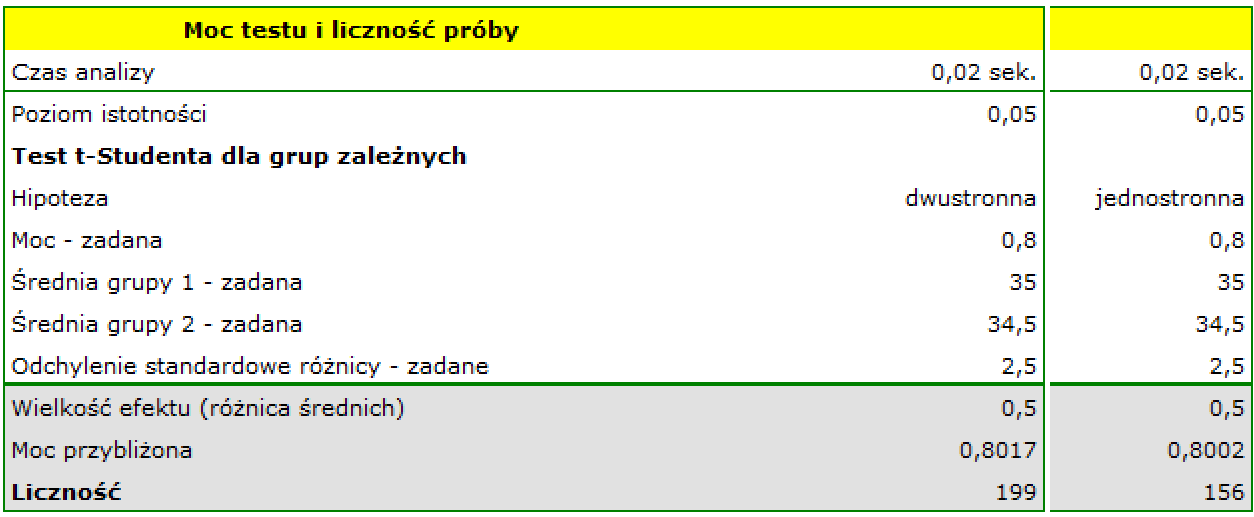
Uzyskana niezbędna liczność to 199 osoby, gdy hipoteza jest dwustronna (tzn. zakładamy, że na skutek diety BMI może spaść lub wzrosnąć) lub 156 osób, gdy hipoteza jest jednostronna (tzn. zakłada jedynie spadek BMI).
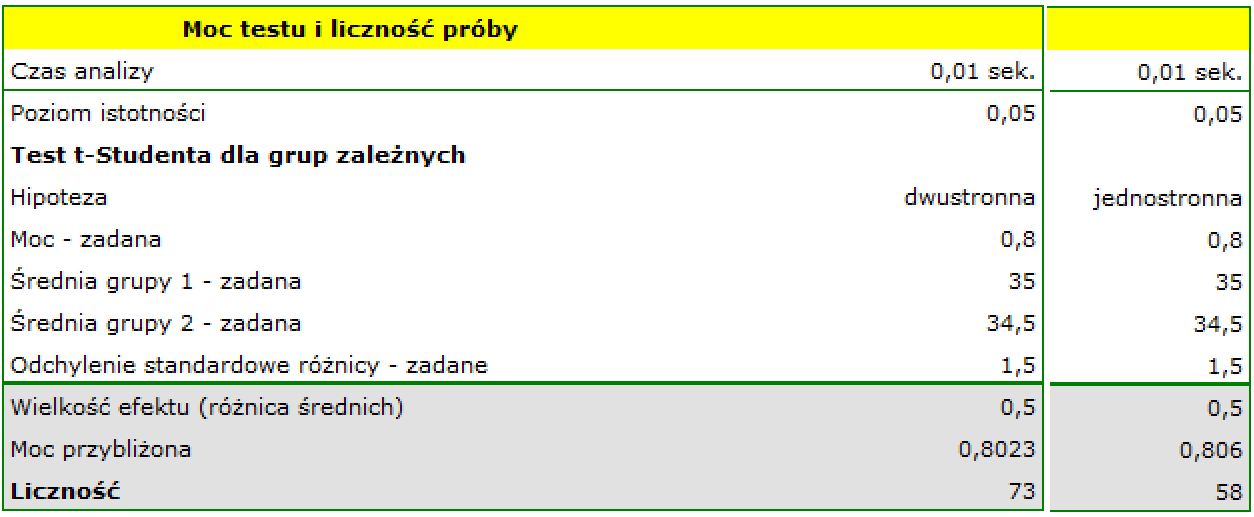
Gdybyśmy założyli, że grupa będzie bardziej zdyscyplinowana i odchylenie standardowe różnicy wyniesie 1.5 jednostki BMI, wówczas próba będzie mogła być nieco mniejsza tzn. 73 osoby w badaniu hipotezy dwustronnej i 58 osób przy hipotezie jednostronnej.
Test t-Studenta dla grup niezależnych
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu t-Studenta dla grup niezależnych warto zapoznać się z zasadami jego stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy:

Uwaga! Gdy znane sa liczności, wówczas wspólne odchylenie standardowe wyraża się wzorem:
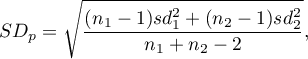
gdy licznosci nie są znane wówczas stosowany jest uproszczony wzór Cohena (Cohen, J. (1988)1))
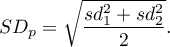
gdzie:
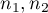
 liczności w pierwszej i drugiej próbie,
liczności w pierwszej i drugiej próbie,
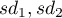
 odchylenia standardowe w pierwszej i drugiej próbie.
odchylenia standardowe w pierwszej i drugiej próbie.
Zadana wielkość efektu, to w tym przypadku wielkość różnicy między średnimi jaką spodziewamy się uzyskać pomiędzy populacjami.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o niecentralny rozkład t-Studenta.
Przykład
Badamy mężczyzn chorych na chorobę X i zdrowych. Chcemy sprawdzić (na poziomie istotności 0.05) czy chorzy różnią się od zdrowych poziomem cholesterolu HDL. Przy czym za istotną klinicznie różnicę uznajemy wielkość 2 mg/dl. Jak dużą próbę należy zebrać by różnica tej wielkości była istotna statystycznie w teście t-Studenta dla grup niezależnych?
Jako średnią HDL dla mężczyzn chorych podajemy 40 mg/dl, a dla osób zdrowych 42 mg/dl. Stostunek liczności obu grup to 1, ponieważ zakładaliśmy równoliczne grupy. Dysponujemy danymi z badania pilotażowego, stąd podajemy odchylenie standardowe dla chorych (13 mg/dl) i zdrowych (11 mg/dl) wskazując dodatkowe opcje  . Moc analizy, jaką chcemy uzyskać to 80%.
. Moc analizy, jaką chcemy uzyskać to 80%.
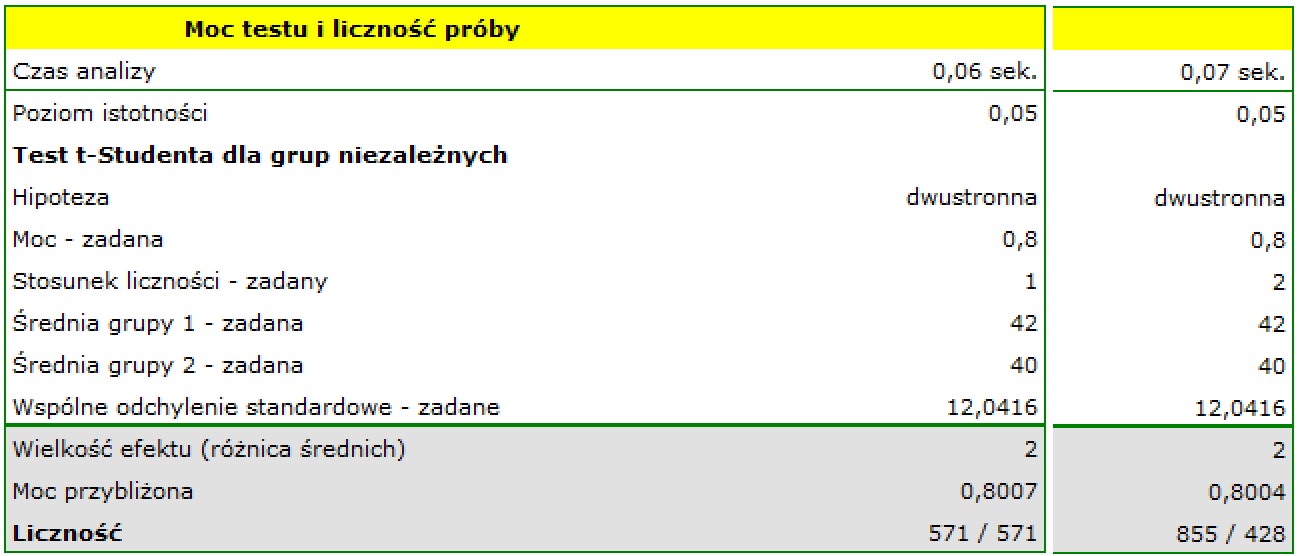
Uzyskana niezbędna liczność to 571 osób, gdy grupy są równoliczne (tzn. zakładamy, że na skutek n1/n2=1) lub n1 = 855 a n2 = 428, gdy nie są równoliczne (tzn. zakładamy stosunek liczności n1/n2=2)
Test chi-kwadrat wariancji pojedynczej próby
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu chi-kwadrat wariancji pojedynczej próby warto zapoznać się z zasadami jego stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy:

Zadana wielkość efektu, to w tym przypadku iloraz odchylenia standardowego populacji badanej i odchylenia hipotetycznego.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o rozkład chi-kwadrat.
Przykład
Przed przystąpieniem do produkcji kolejnej partii pewnego syropu przeciwkaszlowego należy dokonać kontrolnych pomiarów objętości syropu nalewanego do butelek. W butelkach powinno się znaleźć 200 ml syropu. Z dokumentacji technicznej urządzenia dozującego wynika, że dopuszczalny rozrzut objętości syropu mierzony za pomocą odchylenia standardowego wynosi 1 ml. Należy sprawdzić (na poziomie istotności 0.05), czy testowane urządzenie działa prawidłowo. Czy próbka składająca się z 20 butelek będzie wystarczająca, by wykazać nadmierny błąd urządzenia, jeśli taki zaistnieje? Za nadmierny błąd urządzenia uznano odchylenie standardowe przekraczające 1.2 ml.
Ponieważ oczekujemy, że odchylenie standardowe dla urządzenia dozującego będzie takie jak w dokumentacji wpisujemy wartość 1 ml jako wartość hipotetyczną. Zbyt duży błąd uzyskamy wtedy, gdy odchylenie przekroczy 1.2 ml i tą wartość wpisujemy w polu dotyczącym odchylenia standardowego grupy butelek, którą będziemy badać.
Jeśli próba będzie liczyła 20 butelek, to uzyskana moc przy hipotezie dwustronnej wyniesie zaledwie 0.25, a zakładając hipotezę jednostronną 0.34. Są to wartości niskie bo mniej niż 35% losównych prób tej wielkości pozwoli wykryć przekroczenie rozrzutu o 0.2 ml.
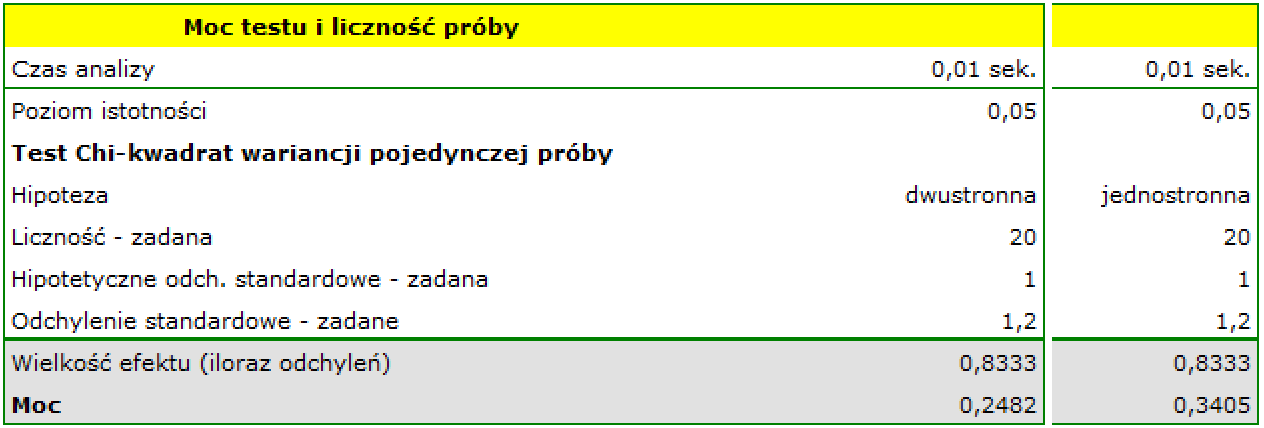
Trzeba uznać, że 20 butelek, to zbyt mała grupa by udowodnić zbyt duże odchylenie standardowe urządzenia, jeśli takie rzeczywiście zaistnieje. Chcielibyśmy uzyskać standardową moc.
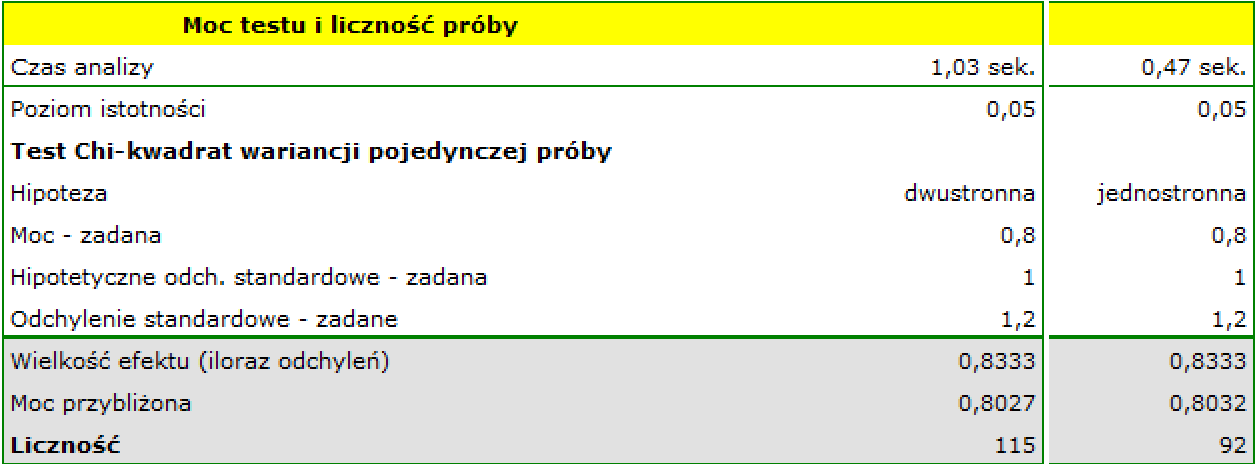
By uzyskać moc równą 80% zmieniamy ustawienia programu i wyliczamy niezbędną liczność, która w tym przypadku wyniesie 115 w hipotezie dwustronnej i 92 w jednostronnej.
Test chi-kwadrat dwóch wariancji Fishera-Snedecora
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu Fishera-Snedecora warto zapoznać się z zasadami jego stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy:

Zadana wielkość efektu, to w tym przypadku iloraz odchylenia standardowego populacji pierwszej i drugiej.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o rozkład F-Snedecora.
Przykład
Przed przystąpieniem do produkcji kolejnej partii pewnego syropu przeciwkaszlowego należy dokonać kontrolnych pomiarów objętości syropu nalewanego do butelek. W butelkach powinno się znaleźć 300 ml syropu. W rozlewni stosowane są dwa urządzenia dozujące. Chcemy sprawdzić (na poziomie istotności 0.05), czy rozrzut objętości syropu mierzony za pomocą odchylenia standardowego dla obu urządzeń jest taki sam. Przeprowadzono niewielkie badanie pilotażowe i ustalono, że odchylenie standardowe dla pierwszego urządzenia wynosi 1.32 a dla drugiego 1.1. Jeśli różnica będzie niewielka tzn. iloraz obu odchyleń wyniesie poniżej 1.2 (tak jak w badaniu pilotażowym), oba urządzenia będą wykorzystywane zamiennie, jeśli nie, zostanie wybrane to z mniejszym odchyleniem od średniej. Ile losowo wybranych butelek należy zmierzyć by móc wykazać że iloraz wielkości 1.2 jest istotny statystycznie?
Wpisujemy wartość odchyleń standardowych uzyskanych w badaniu pilotażowym i zakładamy 80% mocy testu.
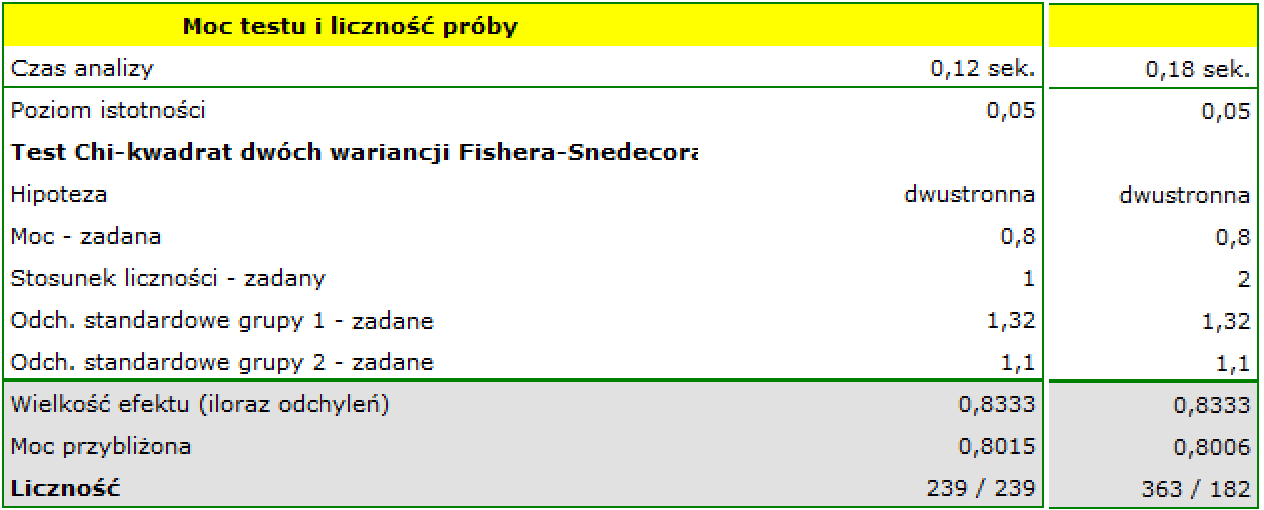
Uzyskana wielkość próby dla każdego urządzenia wynosi n1=n2=239, przy założeniu równolicznych grup (tzn. stosunek n1/n2=1) i n1=363 oraz n2=182 przy założeniu dwukrotnie większej próby dla pierwszego urządzenia (tzn. stosunek n1/n2=2).
Test chi-kwadrat zgodności
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu chi-kwadrat zgodności warto zapoznać się z zasadami jego stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy 2):

Zadana wielkość efektu, czyli 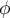 to w tym przypadku pierwiastek z ilorazu statystyki testu chi-kwadrat i liczności grupy badanej:
to w tym przypadku pierwiastek z ilorazu statystyki testu chi-kwadrat i liczności grupy badanej:
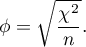 Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o niecentralny rozkład chi-kwadrat.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o niecentralny rozkład chi-kwadrat.
Test chi-kwadrat (RxC)
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu chi-kwadrat dla tabel RxC warto zapoznać się z zasadami jego stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy 3)4):

Zadana wielkość efektu, czyli 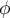 to w tym przypadku pierwiastek z ilorazu statystyki testu chi-kwadrat i liczności grupy badanej:
to w tym przypadku pierwiastek z ilorazu statystyki testu chi-kwadrat i liczności grupy badanej:
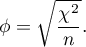
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o niecentralny rozkład chi-kwadrat.
Przykład
Istnieją plany przeprowadzenia szerokiego badania pokazującego stan wiedzy populacji Polski na temat sposobów walki z popularnymi wirusami. W ramach projektu należy ustalić czy działania edukacyjne informujące o nieskuteczności antybiotykoterapii w zakażeniach wirusowych były tak samo skuteczne w starszej grupie wiekowej (tzn. powyżej 50 roku życia) jak u młodszych dorosłych (18-50 lat). Przeprowadzono badanie pilotażowe i losowo wybranej próbie 200 osób zadano pytanie: „Czy antybiotyki zwalczają wirusy?”. Respondenci mieli możliwość wskazania jednej z trzech odpowiedzi: „nie” lub „nie wiem”, „tak”. Wyniki badania pilotażowego przygotowano do publikacji. Poniżej zamieszczono fragment opisu umieszczonego w pracy:
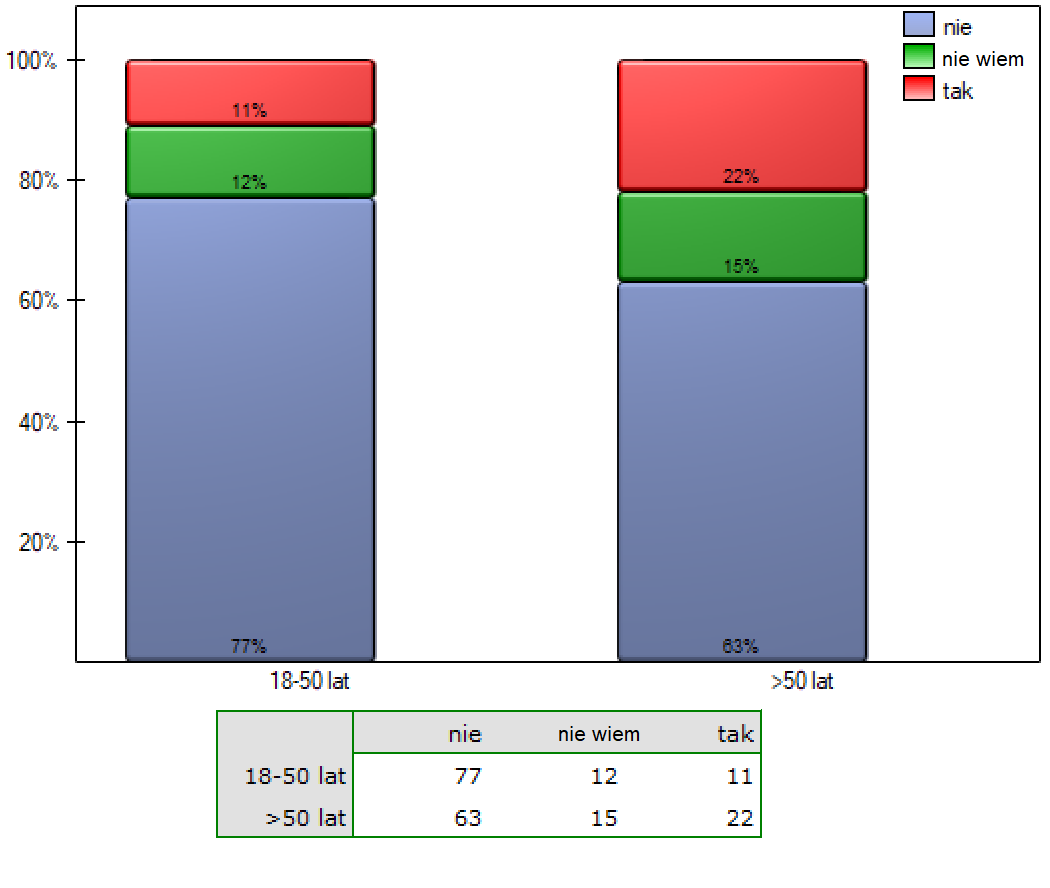
Uzyskana wartość p w teście chi-kwadrat była nieistotna statystycznie p=0.0672.
Słuszne zaskoczenie recenzenta pracy budzi informacja, iż dwukrotnie więcej osób powyżej 50 roku życia błędnie wskazało, iż antybiotyki zwalczają wirusy (22% w stosunku do 11%), jednak różnica ta nie była istotna statystycznie.
Zgodnie z sugestią recenzenta należy sprawdzić, czy brak istotności statystycznej dla tej różnicy nie wynika ze zbyt niskiej mocy testu oraz podać jak duża powinna być próba, by przy zachowaniu tych samych odsetków uzyskać moc testu chi-kwadrat na poziomie 80%?
Przygotowanie odpowiedzi dla recenzenta
Wyznaczymy współczynnik 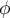 dla uzyskanego testu (menu:
dla uzyskanego testu (menu: Chi-kwadrat, Fisher, OR/RR→Współczynniki korelacji…→Phi). Uzyskujemy 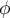 =0.1643.
=0.1643.
Na podstawie 200 elementowej próby, o danych umieszczonych w tabeli o dwóch wierszach i trzech kolumnach oraz zadanej wielkości współczynnika 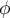 wyznaczamy moc testu chi-kwadrat.
wyznaczamy moc testu chi-kwadrat.
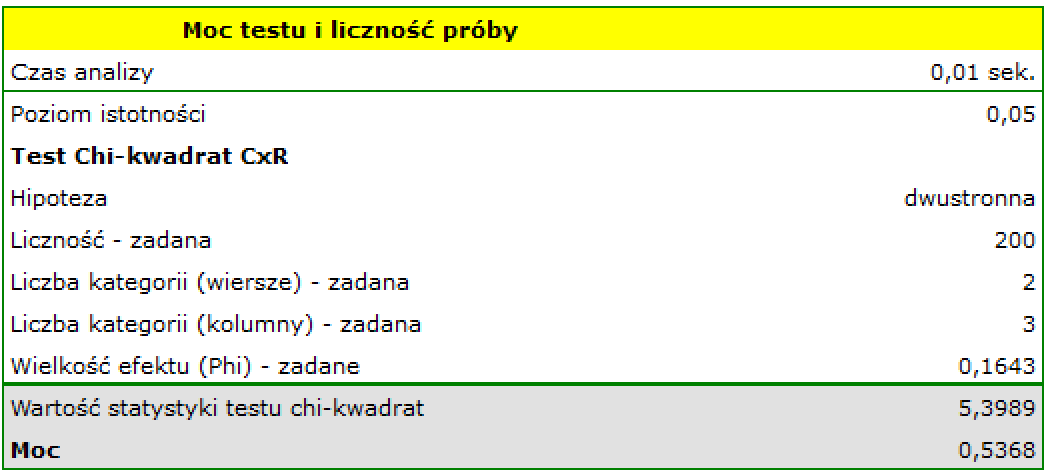
Uzyskana moc w tej analizie jest niewielka i wynosi 0.5368, co wydaje się potwierdzać obawy o niewystarczająco licznej próbie.
Jeśli dla próby o innej liczności uzyskamy ten sam rozkład danych, to oznacza, że uzyskamy również ten sam współczynnik 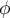 . Do wyznaczenia liczności próby, która dałaby nam 80% moc testu chi-kwadrat, podajemy ponownie współczynnik
. Do wyznaczenia liczności próby, która dałaby nam 80% moc testu chi-kwadrat, podajemy ponownie współczynnik 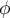 =0.1643.
=0.1643.
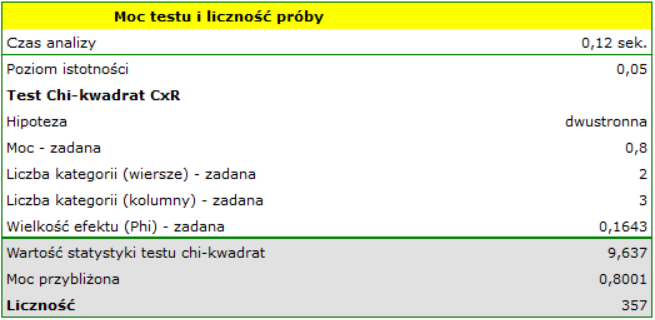
Uzyskujemy informację, że potrzebna będzie próba wielkości 357 ankietowanych. Ponieważ jest to dopiero badanie pilotażowe, planujemy zwiększyć grupę badaną do 357 osób w badaniu właściwym.
Jednak już w tej chwili zauważamy, że przy pominięciu osób niezdecydowanych (tzn. tych, którzy wybrali odpowiedź „nie wiem”) i ponownym przeprowadzeniu analizy, można wykazać istotne różnice (chi-kwadrat, p=0.0251). W grupie osób zdecydowanych odsetki wybierających błędną odpowiedź są ponad dwukrotnie większe na niekorzyść osób >50 lat (12.5% vs 25.9%).
Test dwóch niezależnych proporcji, Chi-kwadrat (2x2)
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu chi-kwadrat dla tabel 2x2 i testu Z dla dwóch niezależnych proporcji warto zapoznać się z zasadami ich stosowania. Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy 5):

Zadana wielkość efektu, to różnica między wyróżnionymi proporcjami.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o rozkład normalny.
Przykład
Rozważmy badanie oceniające skuteczność aspiryny w zmniejszaniu śmiertelności z powodu zawału mięśnia sercowego. Wcześniejsze badania wskazują, że odsetek zgonów z powodu zawału serca wynosi 0.015 dla osób nieużywających i 0.001 dla użytkowników aspiryny. Badacze chcą określić minimalną wielkość próbki wymaganą do wykrycia absolutnej różnicy | 0.001-0.015 | = 0.014 przy 80% mocy za pomocą dwustronnego testu o poziomie istotności 5%.

Zakładając, że grupy będą równoliczne, do każdej z nich trzeba zebrać 635 osób.
ANOVA dla grup niezależnych
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności ANOVA dla grup niezależnych warto zapoznać się z zasadami jej stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy:

Zadana wielkość efektu, to w tym przypadku RMSSE czyli miara standaryzowana stosowana w ANOVA do opisania ogólnego poziomu efektu w populacji.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o niecentralny rozkład F-Snedecora.
Przykład
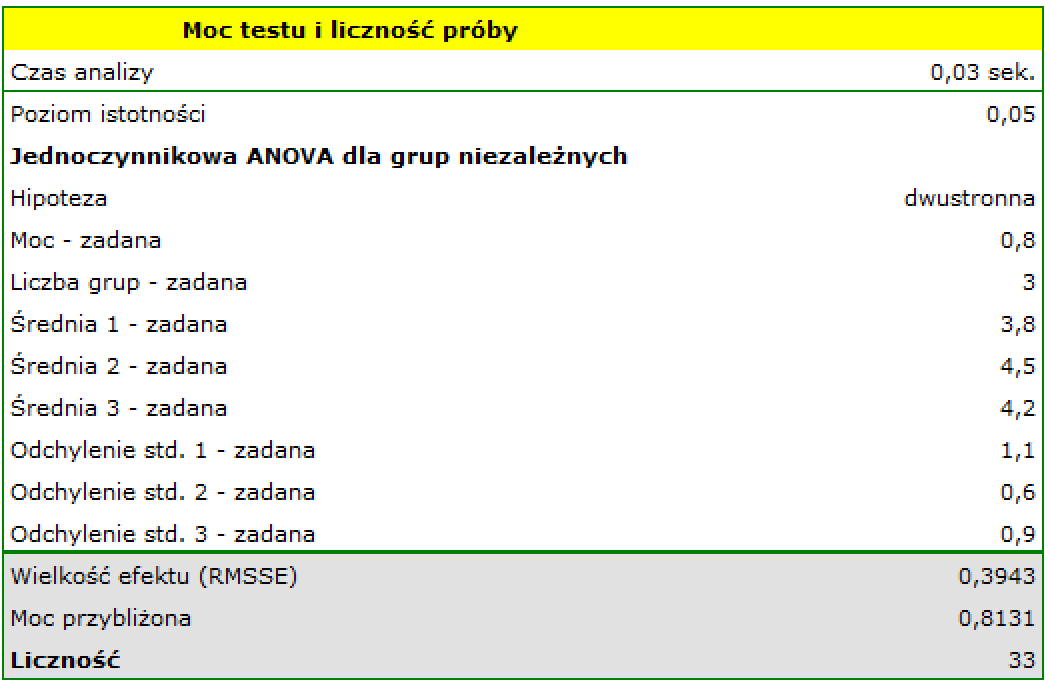
Badano parametr FVC oraz dla pacjentów z wadami serca (wada serca A, wada serca B i wada serca C). Chcemy się dowiedzieć (na poziomie istotności 0.05), czy pacjenci różnią się wartościami tego parametru. By to sprawdzić przeprowadzono najpierw badanie pilotażowe. Na podstawie wyników tego badania ustalono przewidywane wielkości efektów, tzn:
- dla wady serca A: średnia = 3.8, odchylenie standardowe = 1.1,
- dla wady serca B: średnia = 4.5, odchylenie standardowe = 0.6,
- dla wady serca C: średnia = 4.2, odchylenie standardowe = 0.9.
Ile osób należy zebrać, jeśli wielkości te utrzymają się na tym samym poziomie, by udowodnić, że występują istotne statystycznie różnice?
Wpisujemy wartości średnich i odchyleń standardowych. Uzyskana wielkość próby dla każdej z grup badanych to 33 osoby, przy założeniu 80% mocy testu.
Test dla jednej proporcji
Przed przystąpieniem do wyznaczania mocy lub niezbędnej liczności testu dla jednej proporcji warto zapoznać się z zasadami jego stosowania.
Do wyznaczenia mocy testu i niezbędnej liczności próby potrzebujemy:

Zadana wielkość efektu, to w tym przypadku wielkość różnicy między zadaną proporcją w populacji badanej a hipotetyczną, oczekiwaną proporcją.
Moc testu oraz niezbędna liczność próby wyliczana jest w oparciu o rozkład normalny, gdy korzystamy z testu asymptotycznego lub rozkład dwumianowy, gdy korzystamy z testu dokładnego.
Przykład
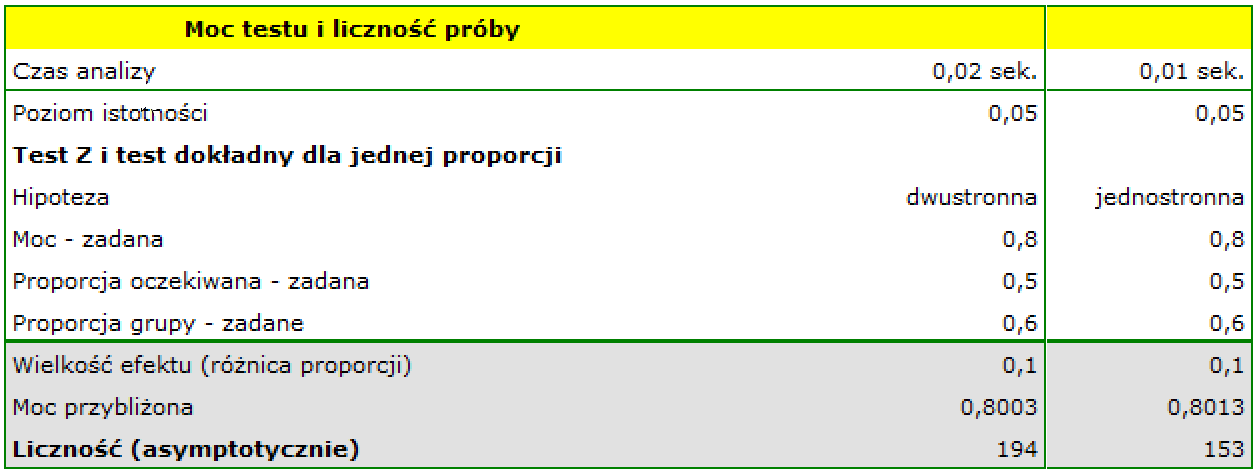
Zapytano 10 wylosowanych rodzin posiadających dzieci w wieku poniżej 10 lat i zamieszkujących w Poznaniu o planowaną przyszłość edukacyjną swoich dzieci. Spośród nich 6 rodziny planowało edukację swoich dzieci na uczelniach wyższych. Jak dużą musielibyśmy zebrać próbę, by na poziomie istotności 0.05 i przy mocy testu równej 0.8 można stwierdzić, że więcej niż 50% poznańskich rodzin posiadających dzieci w wieku poniżej 10 lat, już teraz planuje ich przyszłą edukację na uczelniach wyższych?
Jako oczekiwaną proporcję wpisujemy 0.5, a proporcję grupy 0.6. Uzyskana wielkość próby to 194 rodzin - gdy badana hipoteza jest dwustronna lub 151 rodzin- gdy hipoteza jest jednostronna.
1)
Cohen, J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
2)
, 3)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
4)
Oyeyemi G.M. , Adewara A.A., Adebola F.B. and Salau S.I. (2010), On the Estimation of Power and Sample Size in Test of Independence, Asian Journal of Mathematics and Statistics, 3(3): 139-146
5)
Chow S.C., Shao J., and Wang H. (2008), Sample Size Calculations in Clinical Research, Second Edition. Chapman and Hall/CRC. Boca Raton, Florida.
statpqpl/niezbliczpl/moclicznpl.txt · ostatnio zmienione: 2021/08/25 21:33 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

