Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown2grpl:nparpl:chikw2x2pl
Test chi-kwadrat dla małych tabel
Test ten opiera się na danych zebranych w postaci tabeli kontyngencji 2 cech ( ,
,  ), z których każda ma możliwe 2 kategorie
), z których każda ma możliwe 2 kategorie 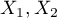 oraz
oraz 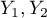 .
.
Okno z ustawieniami opcji testu Chi-kwadrat oraz jego poprawek wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher, OR/RR lub poprzez ''Kreator''.
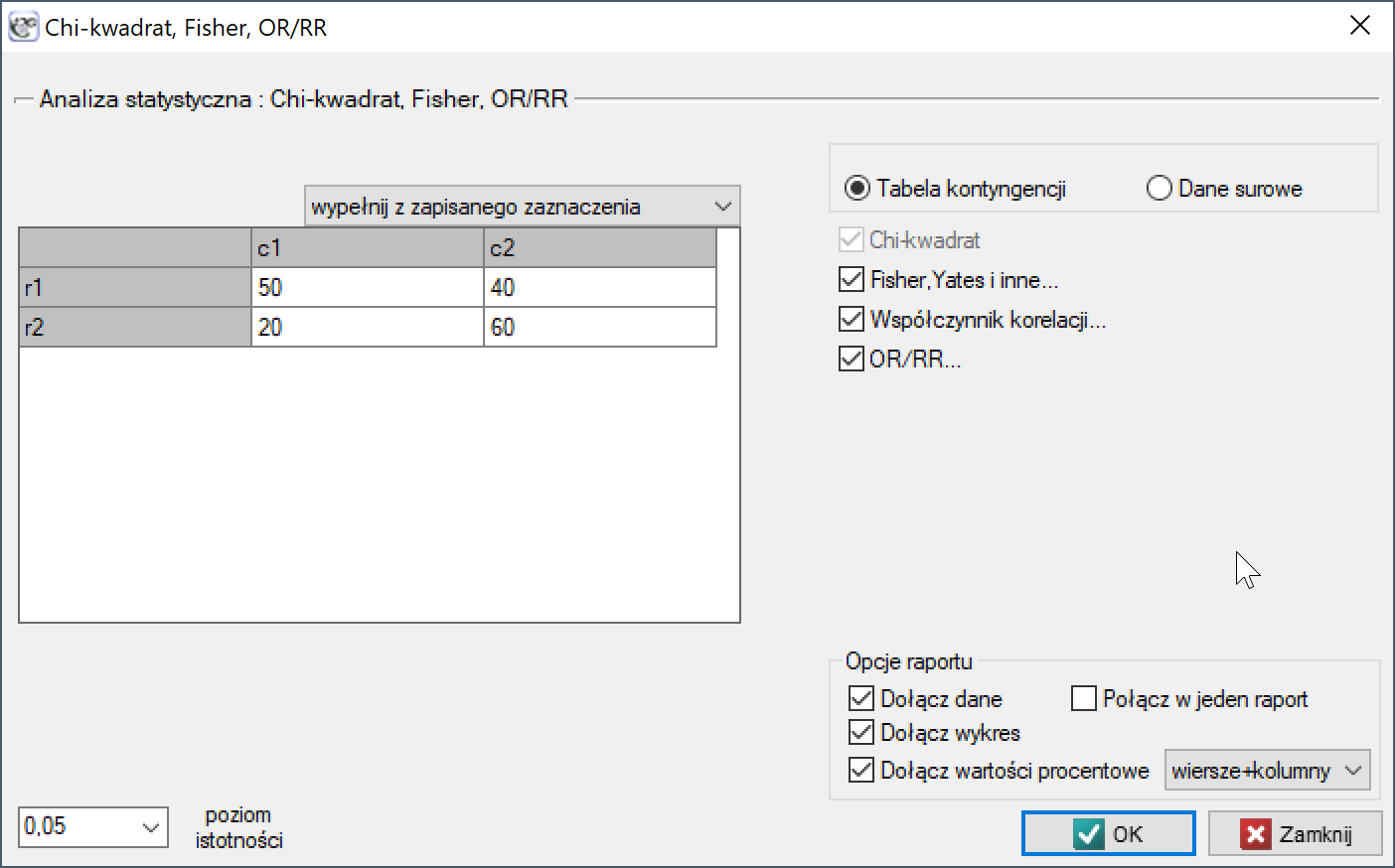
Test  dla tabel
dla tabel 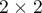 (ang. Pearson's Chi-square test), Karl Pearson 1900. Test ten jest zawężeniem testu chi-kwadrat dla tabel (r x c).
(ang. Pearson's Chi-square test), Karl Pearson 1900. Test ten jest zawężeniem testu chi-kwadrat dla tabel (r x c).
Statystyka testowa ma postać:
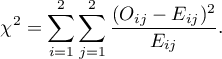
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z jednym stopniem swobody.
Przykład (plik płeć-egzamin.pqs)
Rozpatrzmy próbę składającą się z 170 osób (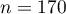 ), dla których badamy 2 cechy (
), dla których badamy 2 cechy ( =płeć,
=płeć,  =zdawalność egzaminu). Każda z tych cech występuje w dwóch kategoriach (
=zdawalność egzaminu). Każda z tych cech występuje w dwóch kategoriach ( =k,
=k,  =m,
=m, 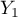 =tak,
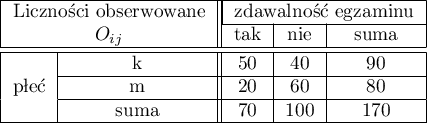
=tak, 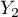 =nie). Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy płcią a zdawalnością egzaminu. Rozkład danych przedstawia tabeli kontyngencji:
=nie). Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy płcią a zdawalnością egzaminu. Rozkład danych przedstawia tabeli kontyngencji:
Hipotezy:
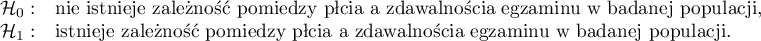
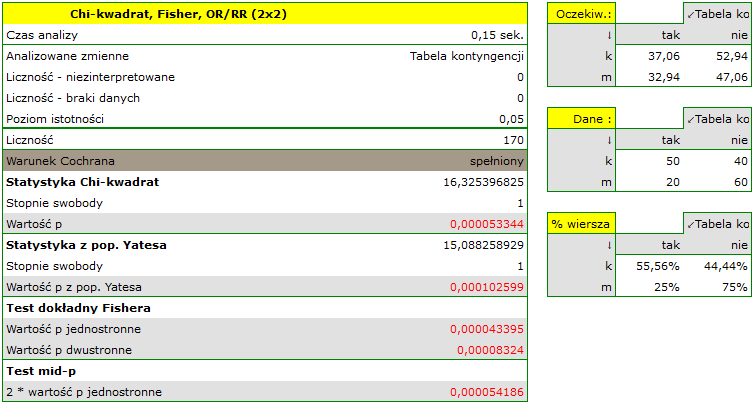
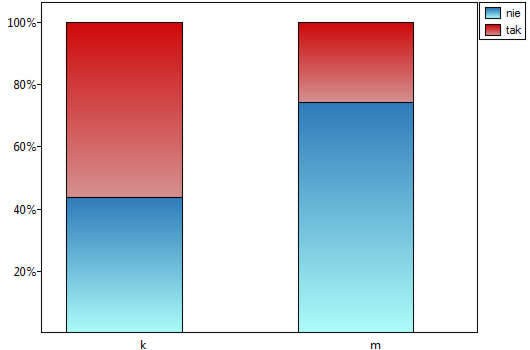
Tabela liczności oczekiwanych nie zawiera wartości mniejszych niż 5. Warunek Cochrana jest spełniony.
Przy przyjętym poziomie istotności  wszystkie wykonane testy potwierdziły prawdziwość hipotezy alternatywnej:
wszystkie wykonane testy potwierdziły prawdziwość hipotezy alternatywnej:
- test chi-kwadrat, wartość
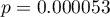 ,
, - test chi-kwadrat z poprawką Yeatesa, wartość
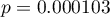 ,
, - test dokładny Fishera, wartość
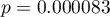 ,
, - test mid-p, wartość
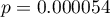
Zatem istnieje zależność pomiędzy płcią a zdawalnością egzaminu w badanej populacji. Istotnie częściej ten egzamin zdają kobiety (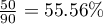 z wszystkich kobiet w próbie zdało egzamin) niż mężczyźni (
z wszystkich kobiet w próbie zdało egzamin) niż mężczyźni (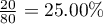 z wszystkich mężczyzn w próbie zdało egzamin)
z wszystkich mężczyzn w próbie zdało egzamin)
statpqpl/porown2grpl/nparpl/chikw2x2pl.txt · ostatnio zmienione: 2020/10/06 14:03 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


