Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown3grpl:nparpl:anova_kwpl
ANOVA Kruskala-Wallisa
Jednoczynnikowa analiza wariancji dla rang Kruskala-Walisa, czyli ANOVA Kruskala-Wallisa (ang. Kruskal-Wallis one-way analysis of variance by ranks) opisana przez Kruskala (1952)1) oraz Kruskala i Wallisa (1952)2) jest rozszerzeniem testu U-Manna-Whitneya na więcej niż dwie populacje. Test ten służy do weryfikacji hipotezy o braku przesunięcia porównywanych rozkładów tzn. najczęsciej nieistotności różnic pomiędzy medianami badanej zmiennej w kilku (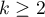 ) populacjach (przy czym zakładamy, że rozkłady zmiennej są sobie bliskie - porównanie wariancji rang można sprawdzić testem dla rang Conovera).
) populacjach (przy czym zakładamy, że rozkłady zmiennej są sobie bliskie - porównanie wariancji rang można sprawdzić testem dla rang Conovera).
Dodatkowe analizy:
- możliwe jest testowanie trendu w ułożeniu badanych grup poprzez wykonanie testu Jonckheere-Terpstra dla trendu.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości średnich rang dla kolejnych populacji lub są upraszczane do median:
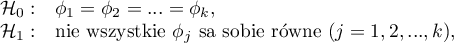
gdzie:
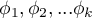 to rozkłady badanej zmiennej w populacjach, z których pobrano próby.
to rozkłady badanej zmiennej w populacjach, z których pobrano próby.
Statystyka testowa ma postać:
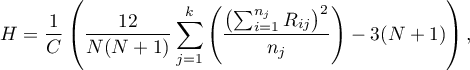
gdzie:
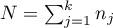 ,
,
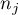 - liczności prób dla
- liczności prób dla  ,
,
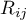 - rangi przypisane do wartości zmiennej, dla
- rangi przypisane do wartości zmiennej, dla 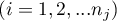 ,
,  ,
,
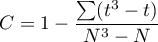 - korekta na rangi wiązane,
- korekta na rangi wiązane,
 - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Wzór na statystykę testową 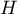 zawiera poprawkę na rangi wiązane
zawiera poprawkę na rangi wiązane  . Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 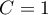 ).
).
Statystyka 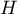 ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru:
ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 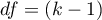 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Dla porównań prostych, zarówno równolicznych jak i różnolicznych grup.
Test Dunna (Dunn 19643)) zawiera poprawkę na rangi wiązane (Zar 20104)) i jest testem korygowanym ze względu na wielokrotne testowanie. Najczęściej wykorzystuje się tu korektę Bonferroniego lub Sidaka, chociaż dostępne są również inne, nowsze korekty opisane szerzej w dziale Wielokrotne porównania.
Przykład - porównania proste (porównanie pomiędzy sobą 2 wybranych median / średnich rang):
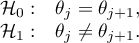
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
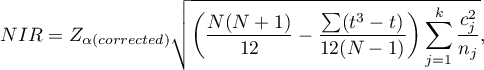
gdzie:

 liczba przypadków wchodzących w skład rangi wiązanej
liczba przypadków wchodzących w skład rangi wiązanej
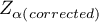 - to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności
- to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności  skorygowanego o liczbę możliwych porównań prostych
skorygowanego o liczbę możliwych porównań prostych  zgodnie z wybraną poprawką.
zgodnie z wybraną poprawką.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
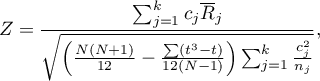
gdzie:
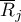 - średnia rang
- średnia rang  -tej grupy, dla
-tej grupy, dla  ,
,
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, ponieważ
zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, ponieważ 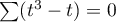 ).
).
Statystyka ta ma asymptotycznie (dla dużych liczności próby) rozkład normalny, a wartość p jest korygowana o liczbę możliwych porównań prostych  zgodnie z wybraną poprawką.
zgodnie z wybraną poprawką.
Nieparametryczny odpowiednik LSD Fishera5), stosowany dla porównań prostych zarówno równolicznych jak i różnolicznych grup.
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
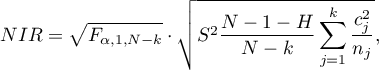
gdzie:
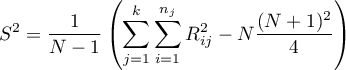
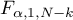 to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz dla stopni swobody odpowiednio: 1 i
oraz dla stopni swobody odpowiednio: 1 i 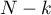 .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
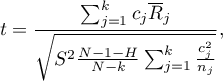
gdzie:
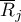 - średnia rang
- średnia rang  -tej grupy, dla
-tej grupy, dla  ,
,
Statystyka ta podlega rozkładowi t-Studenta z 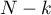 stopniami swobody.
stopniami swobody.
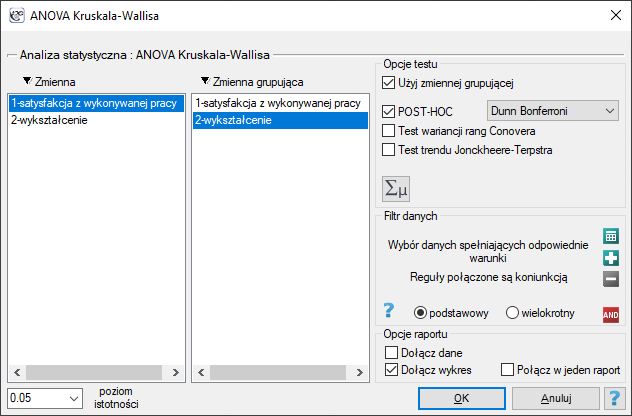
Okno z ustawieniami opcji ANOVA Kruskala-Wallisa wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Kruskala-Wallisa lub poprzez Kreator.
Przykład (satysfakcjaZpracy.pqs)
Przepytano grupę 120 osób, dla których wykonywane zajęcie jest ich pierwszą pracą uzyskaną po otrzymaniu odpowiedniego wykształcenia. Ankietowani oceniali satysfakcję z wykonywanej pracy w pięciostopniowej skali, gdzie:
1- praca niesatysfakcjonująca,
2- praca dająca niewielką satysfakcję,
3- praca dająca przeciętny poziom satysfakcji,
4- praca dająca dość dużą satysfakcję ,
5- praca bardzo satysfakcjonująca.
Sprawdzimy czy poziom deklarowanej satysfakcji z pracy nie zmienia się dla poszczególnych kategorii wykształcenia.
Hipotezy:

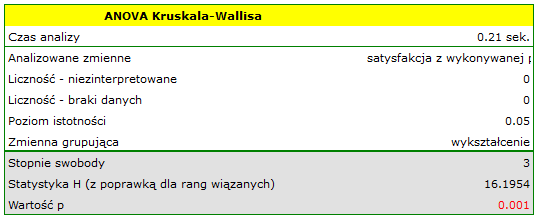
Uzyskana wartość 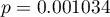 świadczy o istotnej różnicy poziomu satysfakcji pomiędzy porównywanymi kategoriami wykształcenia. Przeprowadzona analiza POST-HOC Dunna z korektą Bonferroniego wskazuje, że istotne różnice dotyczą osób z wykształceniem podstawowym i średnim oraz z wykształceniem podstawowym i wyższym. Nieco więcej różnic możemy potwierdzić wybierająć silniejszy POST-HOC Conover-Iman.
świadczy o istotnej różnicy poziomu satysfakcji pomiędzy porównywanymi kategoriami wykształcenia. Przeprowadzona analiza POST-HOC Dunna z korektą Bonferroniego wskazuje, że istotne różnice dotyczą osób z wykształceniem podstawowym i średnim oraz z wykształceniem podstawowym i wyższym. Nieco więcej różnic możemy potwierdzić wybierająć silniejszy POST-HOC Conover-Iman.
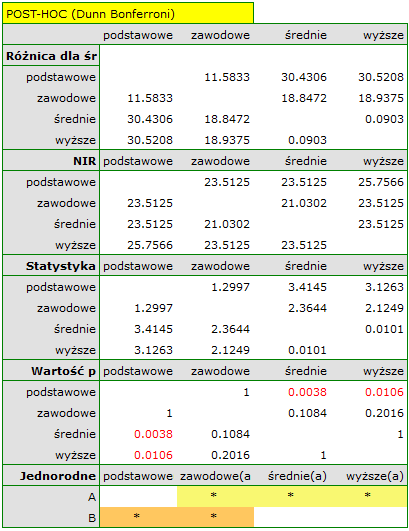
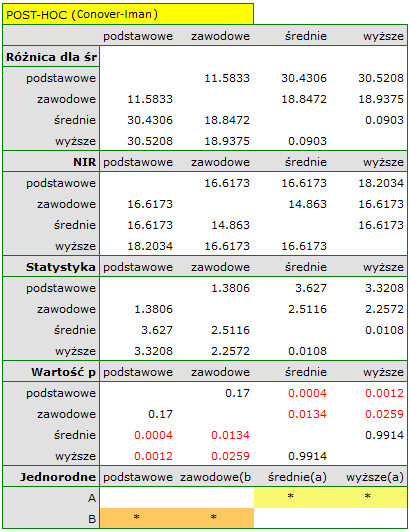
Na wykresie przedstawiającym mediany i kwartyle możemy zobaczyć grupy jednorodne wyznaczone przez test POST-HOC. Jeśli zdecydujemy się na przedstawienie wyników Dunna z korektą Bonferroniego zobaczymy dwie grupy jednorodne, które nie są zupełnie odrębne, tzn. grupę (a) - osoby słabiej oceniające satysfakcję z pracy i grupę (b)- osoby lepiej oceniające tę satysfakcję. Wykształcenie zawodowe przynależy do obydwu tych grup, co oznacza, że osoby z tym wykształceniem oceniają satysfakcję z pracy dość różnorodnie. Ten sam opis grup jednorodnych możemy znaleźć w wynikach testów POST-HOC.
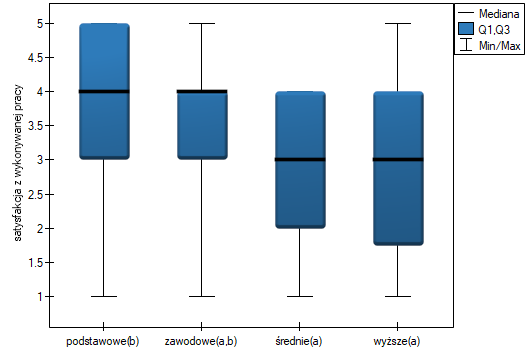
Dokładny opis danych możemy przedstawić wybierając w oknie analizy statystyki opisowe  i wskazując na dodanie do opisu liczności i procentów.
i wskazując na dodanie do opisu liczności i procentów.
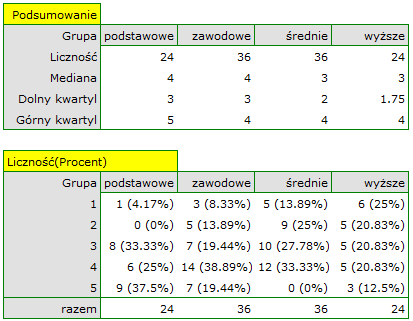
Rozkład odpowiedzi możemy też przedstawić na wykresie liczności.
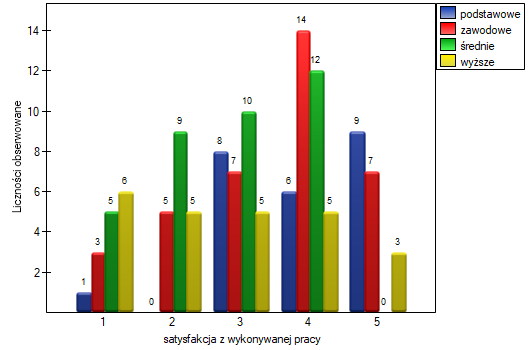
1)
Kruskal W.H. (1952), A nonparametric test for the several sample problem. Annals of Mathematical Statistics, 23, 525-540
2)
Kruskal W.H., Wallis W.A. (1952), Use of ranks in one-criterion variance analysis. Journal of the American Statistical Association, 47, 583-621
3)
Dunn O. J. (1964), Multiple comparisons using rank sums. Technometrics, 6: 241–252
4)
Zar J. H., (2010), Biostatistical Analysis (Fifth Editon). Pearson Educational
5)
Conover W. J. (1999), Practical nonparametric statistics (3rd ed). John Wiley and Sons, New York
statpqpl/porown3grpl/nparpl/anova_kwpl.txt · ostatnio zmienione: 2022/12/03 17:10 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


