Test wariancji rang Conover

Test kwadratów rang Conovera służy, podobnie jak test Fishera-Snedecora (dla 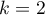$k=2$ ), test Levene i test Browna-Forsythea (dla 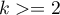$k>=2$ ) do weryfikacji hipotezy podobnym zróżnicowaniu badanej zmiennej w kilku populacjach. Jest on nieparametrycznym odpowiednikiem wskazanych wyżej testów, przez to nie zakłada normalności rozkładu danych i opiera się na rangach ¹⁾. Jednak test ten bada zróżnicowanie, a więc odległości do średniej, dlatego podstawowym warunkiem jego stosowania jest:

pomiar na skali interwałowej,

Hipotezy:

$\begin{array}{cc} \mathcal{H}_0: & $rozproszenie danych w porównywanych populacjach jest takie samo $\\ \mathcal{H}_1: & $przynajmniej dwie populacje różnią się wielkością rozproszenia danych$. \end{array}$

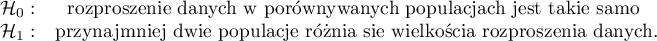
Statystyka testowa ma postać: $\begin{displaymath} \chi^2=\frac{1}{D^2}\left(\sum_{j=1}^k\frac{S_j^2}{n_j}-N\overline{S}^2\right) \end{displaymath}$

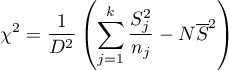
gdzie:

$N=n_1+n_2+...+n_k$ ,

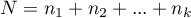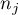$n_j$ - liczność w poszczególnych grupach,

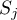$S_j$ - suma kwadratów rang w $j$ -tej grupie,

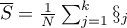$\overline{S}=\frac{1}{N}\sum_{j=1}^k\S_j$ - średnia wszystkich kwadratów rang,

$D^2=\frac{1}{N-1}\left(\sum_{ji=1}^NR_i^4-N\overline{S}^2\right)$ ,

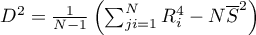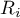$R_i$ -rangi dla wartości przedstawiających odległość pomiaru od średniej danej grupy.

Statystyka ta ma rozkład chi-kwadrat z 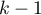$k-1$ stopniem swobody.

wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

Okno z ustawieniami opcji testu wariancji rang Conovera wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Kruskala-Wallisa, opcja testu wariancji rang Conovera lub Statystyka→Testy nieparametryczne→Mann-Whitney, opcja testu wariancji rang Conovera.

Przykład (metodaOperacji.pqs)

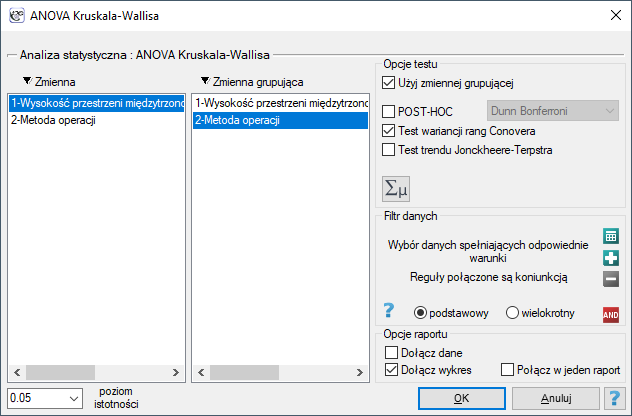
Przygotowano chorych do operacji kręgosłupa. Chorzy będą operowani jedną z trzech metod. Dokonano wstępnego przydziału każdej osoby chorej do poszczególnych typów operacji. Na późniejszym etapie zamierzamy porównywać stan chorych po przebytych operacjach, dlatego zależy nam by grupy chorych były porównywalne. Powinny być podobne min. pod względem wysokości przestrzeni międzytrzonowej (WPMT) przed operacją. Podobieństwo powinno dotyczyć nie tylko wartości przeciętnych ale również zróżnicowania grup.

Sprawdzono rozkład danych.

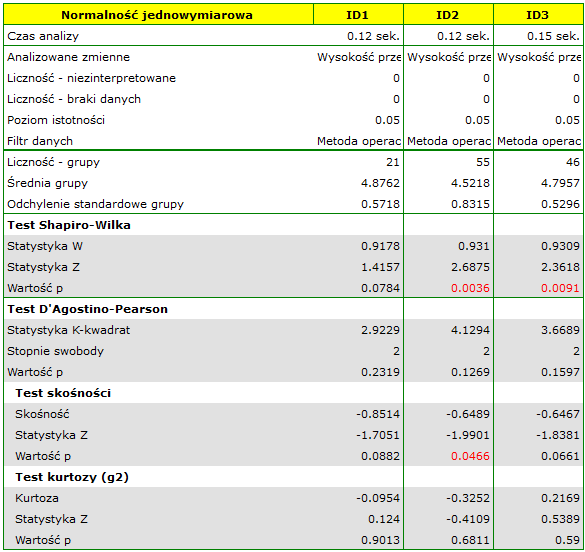
Okazuje się, że w przypadku dwóch metod operacji WPMT wykazuje odstępstwa od normalności, których przyczyną w dużej mierze jest skośność danych. Dalsza analiza porównawcza przeprowadzona zostanie przy pomocy testu Kruskala-Wallisa, by porównać czy poziom WPMT różni się pomiędzy metodami oraz testu Conovera, który wskaże, czy w każdej metodzie rozpiętość wyników WPMT jest podobna.

Hipotezy dla testu wariancji Conovera:

$\begin{array}{cl} \mathcal{H}_0: & $różnorodność (zakres) WPMT jest taka sama dla każdej metody operacji,$\\ \mathcal{H}_1: & $różnorodność (zakres) WPMT jest wyższa/niższa przynajmniej dla jednej metody operacji.$ \end{array}$

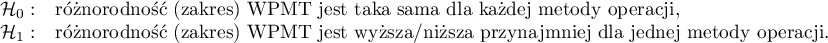
Hipotezy dla testu Kruskala-Wallisa :

$\begin{array}{cl} \mathcal{H}_0: & $poziom WPMT jest taki sam dla każdej metody operacji,$\\ \mathcal{H}_1: & $poziom WPMT jest wyższy/niższy przynajmniej dla jednej metody operacji.$ \end{array}$

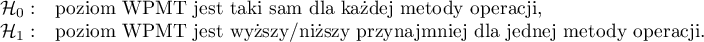
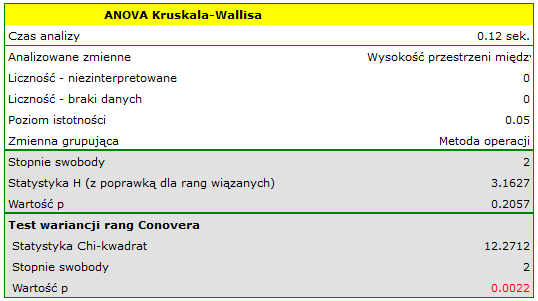
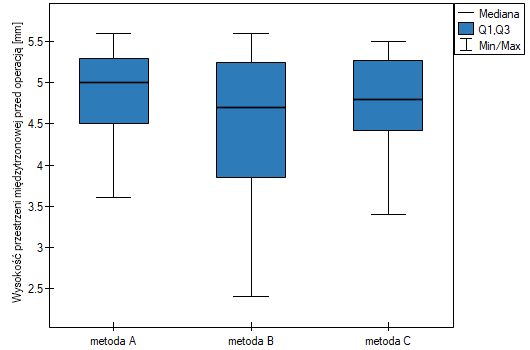
Najpierw interpretacji podlega wartość testu wariancji Conovera, która wskazuje na istotne statystycznie różnice w zakresach porównywanych grup (p=0.0022). Z wykresu możemy wnioskować, że różnice dotyczą głównie grupy 3. Ponieważ wykryto różnice w zakresie WPMT, to interpretacja wyniku testu Kruskala-Wallisa, porównującego poziom WPMT dla tych metod, powinna być ostrożna, gdyż test ten jest wrażliwy na niejednorodność wariancji. Mimo iż test Kruskala-Wallisa nie wykazał istotnych różnic (p=0.2057), to zaleca się by chorych o niskich WPMT (którzy zostali przypisani głównie do operacji metodą B) rozmieścić bardziej równomiernie tzn. by sprawdzić, czy nie można im zaproponować wykonania operacji metodą A lub C. Po ponownym przydziale chorych należy powtórzyć analizę.}

¹⁾

Conover W. J. (1999), Practical nonparametric statistics (3rd ed). John Wiley and Sons, New York

PQStat - Baza Wiedzy

Pasek boczny

Test wariancji rang Conover

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Test wariancji rang Conover

Narzędzia strony