PQStat - Baza Wiedzy

Przykład (plik wydawca.pqs)

Pewien wydawca książek chciał się dowiedzieć, jaki wpływ na zysk brutto ze sprzedaży mają takie zmienne jak: koszty produkcji, koszty reklamy, koszty promocji bezpośredniej, suma udzielonych rabatów, popularność autora. W tym celu przeanalizował 40 pozycji wydanych w ciągu ostatniego roku (zbiór uczący). Fragment danych przedstawia poniższy rysunek:

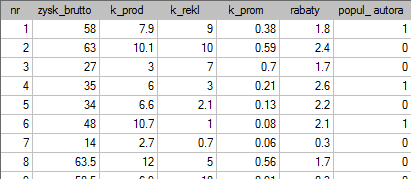
Pięć pierwszych zmiennych wyrażonych jest w tysiącach dolarów - są to więc zmienne zebrane na skali interwałowej. Natomiast ostatnia zmienna: popularność autora to zmienna dychotomiczna, gdzie 1 oznacza autora znanego, 0 oznacza autora nieznanego.

Na podstawie uzyskanej wiedzy wydawca planuje przewidzieć zysk brutto z kolejnej wydawanej książki znanego autora. Koszty, jakie zamierza ponieść to: koszty produkcji 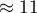, koszty reklamy 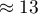, koszty promocji bezpośredniej 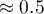, suma udzielonych rabatów .

Budujemy model liniowej regresji wielorakiej dla zbioru uczącego wybierając: zysk brutto jako zmienną zależną , koszty produkcji, koszty reklamy, koszty promocji bezpośredniej, suma udzielonych rabatów, popularność autora jako zmienne niezależne 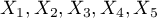. W rezultacie wyliczone zostaną współczynniki równania regresji oraz miary pozwalające ocenić jakość modelu.

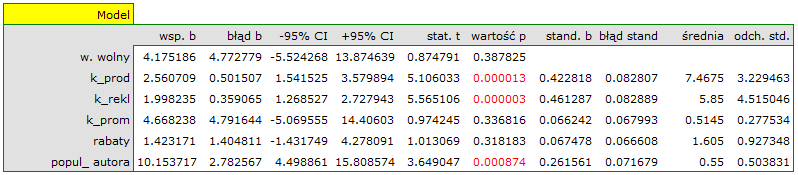
Na podstawie oszacowanej wartości współczynnika , związek pomiędzy zyskiem brutto a wszystkimi zmiennymi niezależnymi możemy opisać równaniem: Uzyskane współczynniki interpretujemy następująco:

• Jeśli koszt produkcji wzrośnie o 1 tysiąc dolarów, to zysk brutto wzrośnie o około 2.56 tysiące dolarów, przy złożeniu, że pozostałe zmienne się nie zmienią;
• Jeśli koszt reklamy wzrośnie o 1 tysiąc dolarów, to zysk brutto wzrośnie o około 2 tysiące dolarów, przy złożeniu, że pozostałe zmienne się nie zmienią;
• Jeśli koszt promocji bezpośredniej wzrośnie o 1 tysiąc dolarów, to zysk brutto wzrośnie o około 4.67 tysiące dolarów, przy złożeniu, że pozostałe zmienne się nie zmienią;
• Jeśli suma udzielonych rabatów wzrośnie o 1 tysiąc dolarów, to zysk brutto wzrośnie o około 1.42 tysiące dolarów, przy złożeniu, że pozostałe zmienne się nie zmienią;
• Jeśli książka została napisana przez autora znanego (oznaczonego przez 1), to w modelu popularność autora przyjmujemy jako wartość 1 i otrzymujemy równanie:

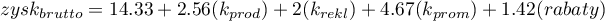Jeśli natomiast książka została napisana przez autora nieznanego (oznaczonego przez 0), to w modelu popularność autora przyjmujemy jako wartość 0 i otrzymujemy równanie: 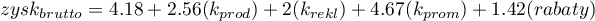Wynik testu t-Studenta uzyskany dla każdej zmiennej wskazuje, że tylko koszt produkcji, koszt reklamy oraz popularność autora wywiera istotny wpływ na otrzymany zysk. Jednocześnie, dla tych zmiennych standaryzowane współczynniki są największe.

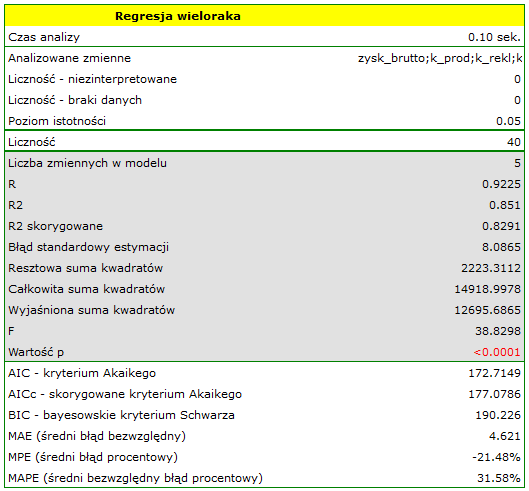
Dodatkowo, model jest dobrze dopasowany o czym świadczy: mały błąd standardowy estymacji 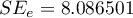, wysoka wartość współczynnika determinacji wielorakiej 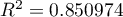i poprawionego współczynnika determinacji wielorakiej 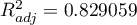oraz wynik testu F analizy wariancji: .

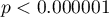Na podstawie interpretacji dotychczasowych wyników możemy przypuszczać, że część zmiennych nie wywiera istotnego wpływu na zysk i może być zbyteczna. Aby model był dobrze sformułowany interwałowe zmienne niezależne powinny być silnie skorelowane ze zmienną zależną i stosunkowo słabo pomiędzy sobą. Możemy to sprawdzić wyliczając macierz korelacji i macierz kowariancji:

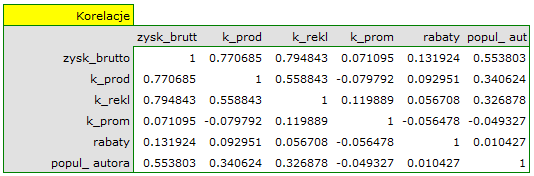
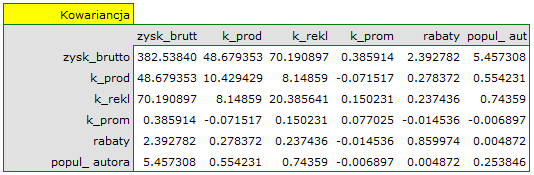
Najbardziej spójną informację, pozwalającą znaleźć te zmienne w modelu, które są zbędne (nadmiarowe) niesie analiza korelacji cząstkowej i semicząstkowej i nadmiarowości:

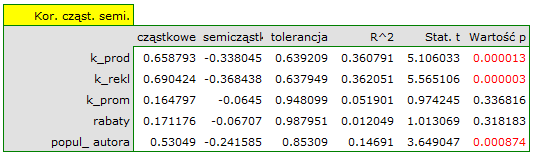
Wartości współczynników korelacji cząstkowej i semicząstkowej wskazują, że najmniejszy wkład w budowany model mają: koszt promocji bezpośredniej i suma udzielonych rabatów. Jednak, są to zmienne najmniej skorelowane z pozostałymi w modelu, o czym świadczy niska wartość i wysoka wartość tolerancji. Ostatecznie, ze statystycznego punktu widzenia, modele bez tych zmiennych nie były by modelami gorszymi niż model obecny (patrz wynik testu t-Studenta dla porównywania modeli). To od decyzji badacza zależy, czy pozostawi ten model, czy zbuduje nowy model pozbawiony kosztów promocji bezpośredniej i sumy udzielonych rabatów. My pozostawiamy model obecny.

Na koniec przeprowadzimy analizę reszt. Fragment tej analizy znajduje się poniżej:

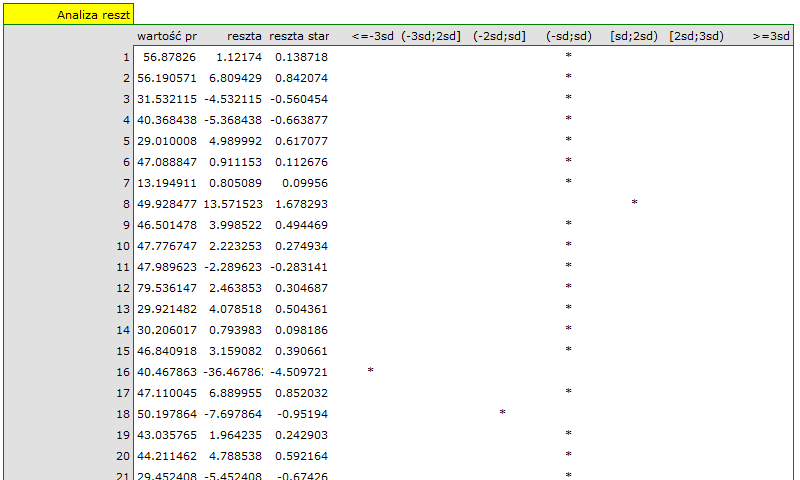
Możemy zauważyć, że jedna z reszt modelu jest obserwacją odstającą jest oddalona o więcej niż 3 odchylenia standardowe od wartości średniej. Jest to obserwacja o numerze 16. Obserwację te możemy łatwo znaleźć kreśląc wykres resz względem obserwowanych lub przewidywanych wartości zmiennej .

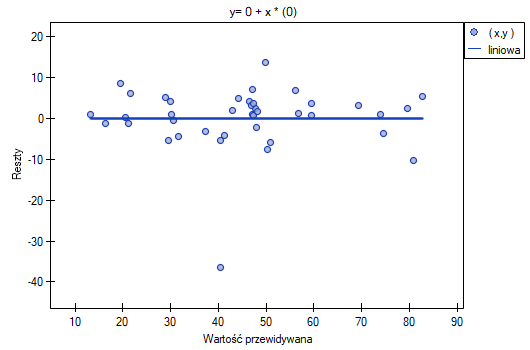
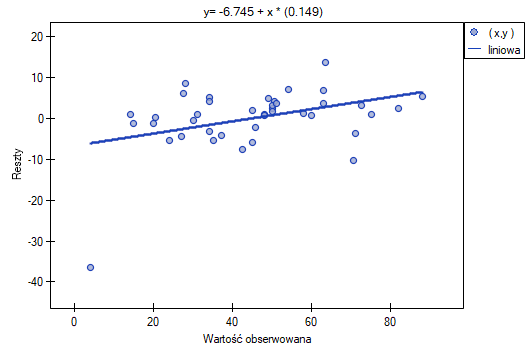
Ten odstający punkt zaburza założenie dotyczące homoskedastyczności. Założenie homoskedastyczności było by spełnione (tzn. wariancja reszt opisana na osi byłaby podobna, gdy przechodzimy wzdłuż osi ), gdybyśmy ten punkt odrzucili. Dodatkowo, rozkład reszt nieco odbiega od rozkładu normalnego (wartość testu Lilieforsa wynosi ):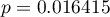

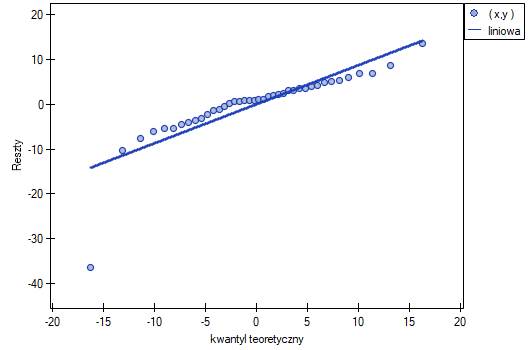
Przyglądając się dokładniej punktowi odstającemu (pozycja 16 w danych do zadania) widzimy, że książka ta jako jedyna wykazuje wyższe koszty niż zysk brutto (zysk brutto = 4 tysiące dolarów, suma kosztów = (8+6+0.33+1.6) = 15.93 tysiące dolarów).

Uzyskany model możemy poprawić usuwając z niego punkt odstający. Wymaga to ponownego przeprowadzenia analizy z włączonym filtrem wykluczającym punkt odstający.

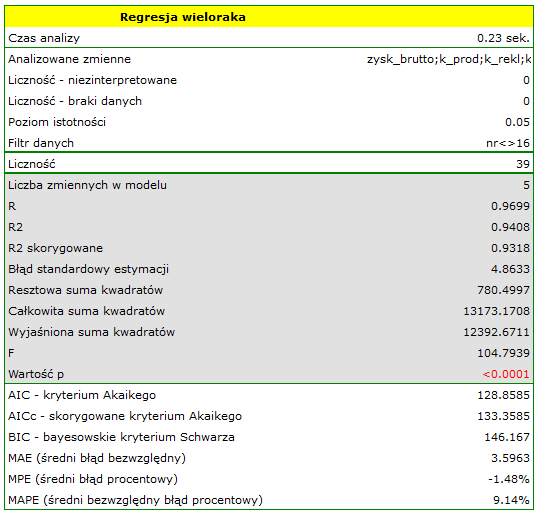
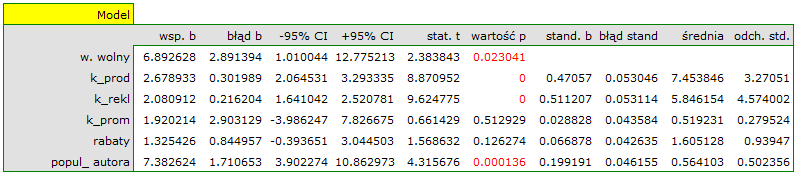
W rezultacie uzyskaliśmy bardzo podobny model, ale obarczony mniejszym błędem i lepiej dopasowany:

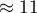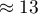Ostatecznie zbudowany model wykorzystamy do predykcji. Na podstawie przewidywanych nakładów w wysokości: koszty produkcji tysięcy dolarów, koszty reklamy tysięcy dolarów, koszty promocji bezpośredniej 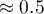tysiąca dolarów, suma udzielonych rabatów 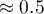tysiąca dolarów,\\oraz faktu, że jest to autor znany (popularność autora 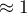) wyliczamy przewidywany zysk brutto wraz z przedziałem ufności:

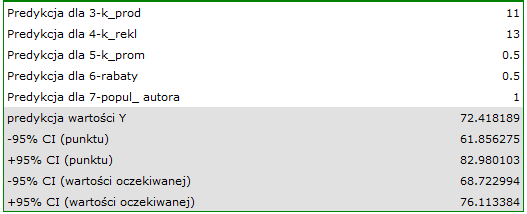
Przewidziany zysk wynosi 72 tysiące dolarów.

Na koniec należy jeszcze zauważyć, że jest to tylko model wstępny. W badaniu właściwym należałoby zebrać więcej danych. Liczba zmiennych w modelu jest bowiem zbyt mała w stosunku do liczby ocenianych książek tzn. n<50+8k