Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Porównanie - 2 grupy » Testy nieparametryczne » Test U Manna-Whitneya
Pasek boczny
statpqpl:porown2grpl:nparpl:mwpl
Test U Manna-Whitneya
Test U Manna-Whitneya (ang. Mann-Whitney U test) znany jest również jako test Wilcoxona Manna-Whitneya (ang. Wilcoxon Mann-Whitney test), Mann i Whitney (1947)1) oraz Wilcoxon (1949)2). Test ten służy do weryfikacji hipotezy o braku przesunięcia porównywanych rozkładów tzn. najczęsciej nieistotności różnic pomiędzy medianami badanej zmiennej w dwóch populacjach (przy czym zakładamy, że rozkłady zmiennej są sobie bliskie - porównanie wariancji rang można sprawdzić testem dla rang Conovera).
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości średnich rang dla porównywanych populacji lub są upraszczane do median:
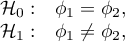
gdzie:
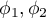 to rozkłady badanej zmiennej w pierwszej i drugiej populacji.
to rozkłady badanej zmiennej w pierwszej i drugiej populacji.
Wyznaczamy wartość statystyki testowej, a na jej podstawie wartość  , którą porównujemy z poziomem istotności
, którą porównujemy z poziomem istotności  :
:

Uwaga!
W zależności od wielkości próby statystyka testowa przyjmuje inną postać:
- Dla małej liczności próby
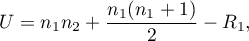
lub
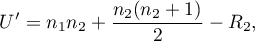
gdzie 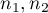 to liczności prób,
to liczności prób, 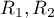 to sumy rang dla prób.
to sumy rang dla prób.
Standardowo interpretacji podlega mniejsza z wartości 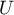 lub
lub 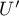 .
.
Statystyka ta podlega rozkładowi Manna-Whitneya i nie zawiera poprawki na rangi wiązane. Wartość dokładnego prawdopodobieństwa z rozkładu Manna-Whitneya wyliczana jest z dokładnością do części setnej ułamka.
- Dla próby o dużej liczności
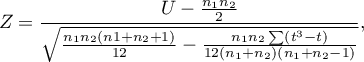
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 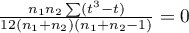 )
)
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Poprawka na ciągłość testu Manna-Whitneya (Marascuilo and McSweeney (1977)3))
Poprawkę na ciągłość stosujemy by zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu normalnego. Wzór na statystykę testową z poprawką na ciągłość wyraża się wtedy:
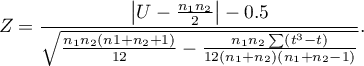
Standaryzowana wielkość efektu
Rozkład statystyki testu Manna-Whitneya jest aproksymowany przez rozkłady normalny, który można przekształcić na wielkość efektu 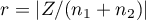 4) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
4) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
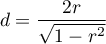
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 5) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu U Manna-Whitneya wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Mann-Whitney lub poprzez ''Kreator''.
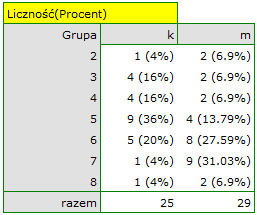
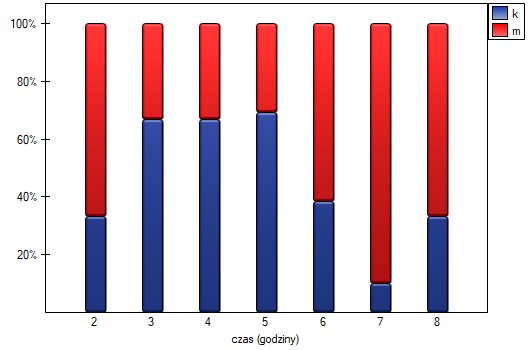
Wysunięto hipotezę, że na pewnej uczelni studenci matematyki spędzają statystycznie więcej czasu przed komputerem niż studentki matematyki. W celu weryfikacji tego przypuszczenia z populacji osób studiujących matematykę na tej uczelni wylosowano próbę liczącą 54 osoby (25 kobiet i 29 mężczyzn). Osoby te zapytano o to jak dużo czasu dziennie spędzają przy komputerze (czas w godzinach) i otrzymano następujące wyniki:
(czas, płeć): (2, k) (2, m) (2, m) (3, k) (3, k) (3, k) (3, k) (3, m) (3, m) (4, k) (4, k) (4, k) (4, k) (4, m) (4, m) (5, k) (5, k) (5, k) (5, k) (5, k) (5, k) (5, k) (5, k) (5, k) (5, m) (5, m) (5, m) (5, m) (6, k) (6, k) (6, k) (6, k) (6, k) (6, m) (6, m) (6, m) (6, m) (6, m) (6, m) (6, m) (6, m) (7, k) (7, m) (7, m) (7, m) (7, m) (7, m) (7, m) (7, m) (7, m) (7, m) (8, k) (8, m) (8, m).}
Hipotezy:


Na podstawie przyjętego poziomu  i statystyki
i statystyki  testu Manna-Whitneya bez poprawki na ciągłość (
testu Manna-Whitneya bez poprawki na ciągłość ( =0.015441) jak i z tą poprawką
=0.015441) jak i z tą poprawką 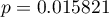 , jak też na podstawie dokładnej statystyki
, jak też na podstawie dokładnej statystyki  (
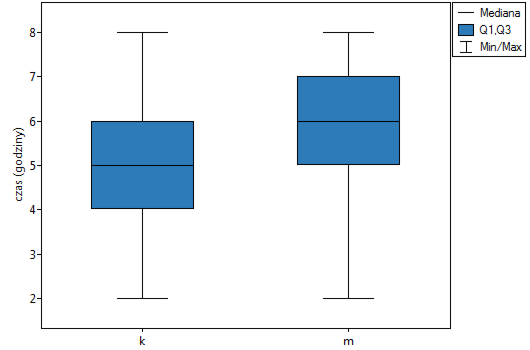
( =0.014948) możemy przyjąć, że istnieją ważne statystycznie różnice pomiędzy studentkami a studentami matematyki w ilości czasu spędzanego przed komputerem. Różnice te polegają na tym, że studentki spędzają mniej czasu przed komputerem niż studenci. Opisać je można na podstawie mediany, kwartyli oraz wartości największej i najmniejszej, które widzimy również na wykresie typu ramka-wąsy. Innym sposobem opisu różnic jest przedstawienie czasu spędzonego przed komputerem na podstawie tabeli liczności i procentów (które uruchamiamy w oknie analizy ustawiając statystyki opisowe
=0.014948) możemy przyjąć, że istnieją ważne statystycznie różnice pomiędzy studentkami a studentami matematyki w ilości czasu spędzanego przed komputerem. Różnice te polegają na tym, że studentki spędzają mniej czasu przed komputerem niż studenci. Opisać je można na podstawie mediany, kwartyli oraz wartości największej i najmniejszej, które widzimy również na wykresie typu ramka-wąsy. Innym sposobem opisu różnic jest przedstawienie czasu spędzonego przed komputerem na podstawie tabeli liczności i procentów (które uruchamiamy w oknie analizy ustawiając statystyki opisowe  ) lub na podstawie wykresu kolumnowego.
) lub na podstawie wykresu kolumnowego.
1)
Mann H. and Whitney D. (1947), On a test of whether one of two random variables is stochastically larger than the other. Annals of Mathematical Statistics, 1 8 , 5 0 4
2)
Wilcoxon F. (1949), Some rapid approximate statistical procedures. Stamford, CT: Stamford Research Laboratories, American Cyanamid Corporation
3)
Marascuilo L.A. and McSweeney M. (1977), Nonparametric and distribution-free method for the social sciences. Monterey, CA: Brooks/Cole Publishing Company
4)
Fritz C.O., Morris P.E., Richler J.J.(2012), Effect size estimates: Current use, calculations, and interpretation. Journal of Experimental Psychology: General., 141(1):2–18.
5)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
statpqpl/porown2grpl/nparpl/mwpl.txt · ostatnio zmienione: 2022/12/03 16:59 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


 liczba przypadków wchodzących w skład
liczba przypadków wchodzących w skład 