PQStat - Baza Wiedzy

The linear correlation coefficients

The Pearson product-moment correlation coefficient 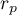$r_p$ called also the Pearson's linear correlation coefficient (Pearson (1896,1900)) is used to decribe the strength of linear relations between 2 features. It may be calculated on an interval scale as long as there are no measurement outliers and the distribution of residuals or the distribution of the analyed features is a normal one.

$\begin{displaymath} r_p=\frac{\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum_{i=1}^n(x_i-\overline{x})^2}\sqrt{\sum_{i=1}^n(y_i-\overline{y})^2}}, \end{displaymath}$

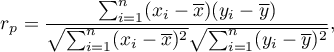
where:

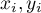$x_i, y_i$ - the following values of the feature $X$ and $Y$ ,

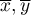$\overline{x}, \overline{y}$ - means values of features: $X$ and $Y$ ,

$n$ - sample size.

Note

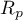$R_p$ – the Pearson product-moment correlation coefficient in a population;

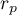$r_p$ – the Pearson product-moment correlation coefficient in a sample.

The value of 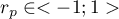$r_p\in<-1; 1>$ , and it should be interpreted the following way:

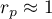$r_p\approx1$ means a strong positive linear correlation – measurement points are closed to a straight line and when the independent variable increases, the dependent variable increases too;
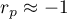$r_p\approx-1$ means a strong negative linear correlation – measurement points are closed to a straight line, but when the independent variable increases, the dependent variable decreases;
if the correlation coefficient is equal to the value or very closed to zero, there is no linear dependence between the analysed features (but there might exist another relation - a not linear one).

Graphic interpretation of 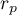$r_p$ .

$\begin{pspicture}(0,-.8)(12.5,2.5) \psline{->}(.5,0)(.5,2) \psline{->}(.5,0)(2.5,0) \rput(.8,1){*} \rput(1.7,.9){*} \rput(1,.7){*} \rput(1.3,1.6){*} \rput(1.5,1){*} \rput(1.1,.4){*} \rput(2.1,1){*} \rput(1.9,1.8){*} \rput(.2,2){$y$} \rput(2.5,-.2){$x$} \rput(1.5,-.7){$r_p\approx0$} \psline{->}(4.5,0)(4.5,2) \psline{->}(4.5,0)(6.5,0) \psline{-}(4.7,.5)(6.3,1.8) \rput(4.8,.7){*} \rput(5.3,1){*} \rput(5,.4){*} \rput(6,1.7){*} \rput(5.7,1.2){*} \rput(4.2,2){$y$} \rput(6.5,-.2){$x$} \rput(5.5,-.7){$r_p\approx1$} \psline{->}(8.5,0)(8.5,2) \psline{->}(8.5,0)(10.5,0) \psline{-}(8.7,1.8)(10.3,.2) \rput(9.6,.9){*} \rput(8.9,1.4){*} \rput(9.7,1.2){*} \rput(10.1,.2){*} \rput(9.9,.4){*} \rput(8.2,2){$y$} \rput(10.5,-.2){$x$} \rput(9.5,-.7){$r_p\approx-1$} \end{pspicture}$

If one out of the 2 analysed features is constant (it does not matter if the other feature is changed), the features are not dependent from each other. In that situation 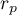$r_p$ can not be calculated.

Note

You are not allowed to calculate the correlation coefficient if: there are outliers in a sample (they may make that the value and the sign of the coefficient would be completely wrong), if the sample is clearly heterogeneous, or if the analysed relation takes obviously the other shape than linear.

The coefficient of determination: 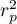$r_p^2$ – reflects the percentage of a dependent variable a variability which is explained by variability of an independent variable.

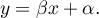
A created model shows a linear relationship: 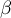$\begin{displaymath} y=\beta x+\alpha. \end{displaymath}$ $\beta$ and $\alpha$ coefficients of linear regression equation can be calculated using formulas: $\begin{displaymath} \displaystyle{\beta=\frac{\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sum_{i=1}^n(x_i-\overline{x})^2}}, \qquad \alpha=\overline{y}-\beta\overline{x}. \end{displaymath}$

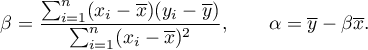
EXAMPLE cont. (age-height.pqs file)

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

The linear correlation coefficients

Narzędzia strony