Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:warstwpl:mhpl:rrpl
The Mantel-Haenszel Relative Risk
If all tables (created by individual stratas) are homogeneous (the Chi-square test of homogeneity for the RR), can check this condition), then, on the basis of these tables, the pooled relative risk with the confidence interval can be designated. Such relative risk is a weighted mean for a relative risk designated for the individual stratas. The usage of the weighted method, proposed by Mantel and Haenszel allows to include the contribution of the strata weights. Each strata of the input has an influence on the pooled relative risk construction (the greater size of the strata, the greater weight and the greater influence on the pooled relative risk).
Weights for individual stratas are designated according to the following formula:
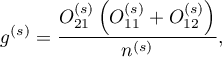
and the Mantel-Haenszel relative risk:
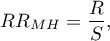
where:
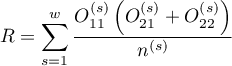 ,
,
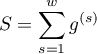 .
.
The confidence interval for 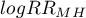 is designated on the basis of the standard error calculated according to the following formula:
is designated on the basis of the standard error calculated according to the following formula:
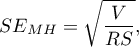
where:
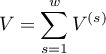 ,
,
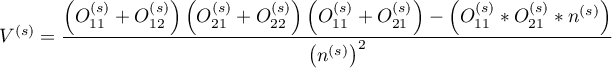 .
.
The Manel-Hanszel Chi-square test for the 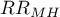
The Mantel-Haenszel Chi-square test for the 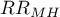 is used in the hypothesis verification about the significance of designated relative risk (
is used in the hypothesis verification about the significance of designated relative risk (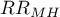 ). It should be calculated for large frequencies, in a contingency table.
). It should be calculated for large frequencies, in a contingency table.
Hypotheses:
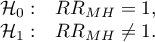
The test statistic is defined by:
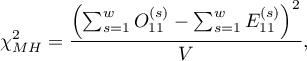
where:
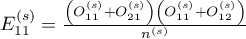 are the expected frequencies in the first contingency table cell, for individual stratas
are the expected frequencies in the first contingency table cell, for individual stratas 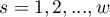 .
.
This statistic asymptotically (for large frequencies) has the Chi-square distribution with 1 degree of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:
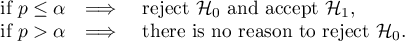
The Chi-square test of homogeneity for the 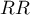
The Chi-square test of homogeneity for the 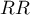 is used in the hypothesis verification that the variable creating stratas, is the modifying effect, i.e. it influences on the designated relative risk in the manner that, the relative risks are significant different for individual stratas.
is used in the hypothesis verification that the variable creating stratas, is the modifying effect, i.e. it influences on the designated relative risk in the manner that, the relative risks are significant different for individual stratas.
Hypotheses:
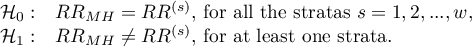
The test statistic, using weighted least squares method, is defined by:
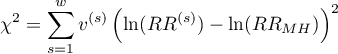
where:
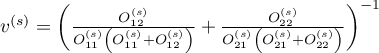 .
.
This statistic asymptotically (for large frequencies) has the Chi-square distribution with the number of degrees of freedom calculated using the formula: 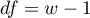 .
.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:
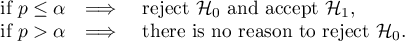
en/statpqpl/warstwpl/mhpl/rrpl.txt · ostatnio zmienione: 2022/02/13 18:25 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

