Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:metapl:skumul
Meta-analiza skumulowana
Typowym celem przeprowadzenia meta-analizy skumulowanej jest pokazanie jak zmienił się efekt od czasu przeprowadzenia/opublikowania ostatniej meta-analizy dotyczącej danego tematu, lub jak zmieniał się na przestrzeni ostatnich lat. Wówczas chronologicznie (zgodnie z linią czasu) dodawane są kolejne badania i każdorazowo wyliczany efekt podsumowujący. Równie ważna jest skumulowana analiza w badaniu zmiany efektu podsumowującego w zależności od wielkości wpływu wybranego, dodatkowego czynnika. Wówczas badania są sortowane zgodnie z wielkością tego czynnika i dla kolejno dodawanych badań wyliczany jest wspólny efekt podsumowujący.
W zależności od celu, któremu ma służyć kumulacja należy wybrać zmienną wg której poszczególne badania będą sortowane, czyli ustalić kolejność dodawania badań do podsumowania meta-analizą. Może to być dowolna zmienna liczbowa.
Przypisana do danego badania wartość udziału skumulowanego definiuje odsetek jaki stanowi łączna waga włączonych do analizy badań tzn. danego badania i badań go poprzedzających. Zmiana precyzji informuje natomiast jak zmieni się precyzja efektu podsumowującego (szerokość przedziału ufności), gdy dane badanie zostanie dołączone do badań go poprzedzających.
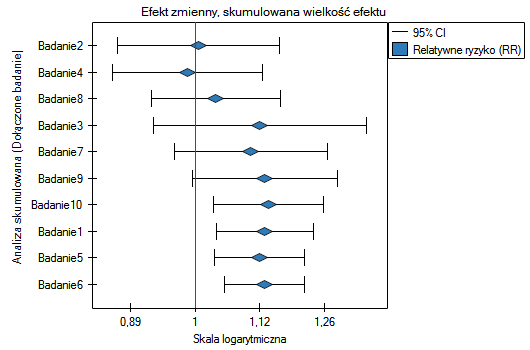
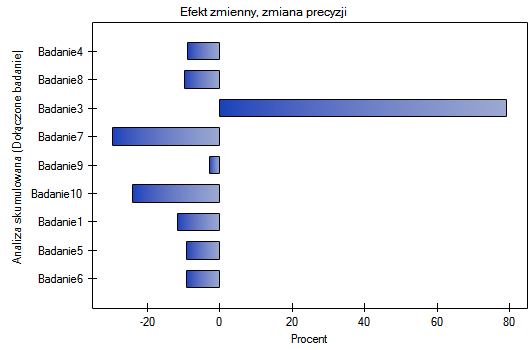
Dobrym zilustrowaniem analizy skumulowanej jest wykres leśny wielkości efektu i wykres zmian precyzji, przy dołączaniu poszczególnych badań.
Przykład c.d. (plik MetaanalizaRR.pqs)
Badając wpływ palenia papierosów na wystąpienie choroby X sprawdzono jak uzyskane wyniki ewaluowały w czasie. W tym celu, w oknie analizy wybrano opcję Meta-analiza skumulowana i zmienną według której kolejne prace będą włączane do meta-analizy, oraz wskazano wykres leśny (skumulowany) i wykres słupkowy (skumulowany).
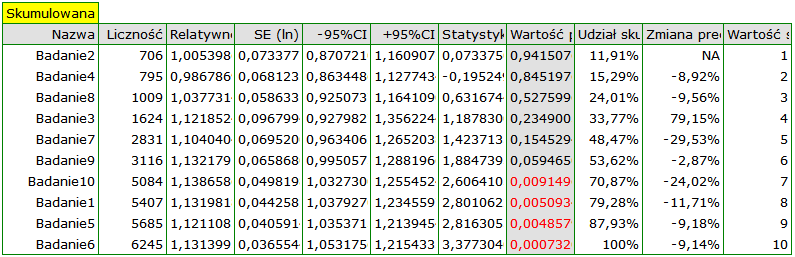
Wraz z pojawianiem się nowych prac uzyskiwany efekt podsumowujący zyskiwał na sile, a jego istotność uzyskano dodając do wcześniejszych prac Badanie 10, a następnie również kolejne badania. Zasadniczo dodanie kolejnych prac zwiększało precyzję uzyskanego relatywnego ryzyka, za wyjątkiem sytuacji, w której dodano Badanie 3. Przedział ufności podsumowującego relatywnego ryzyka poszerzył się wówczas o 79.15%. Efekt ten widzimy w tabeli oraz na dołączonych wykresach. W rezultacie należy się zastanowić nad wykluczeniem Badania 3 z przeprowadzonej meta-analizy.
statpqpl/metapl/skumul.txt · ostatnio zmienione: 2020/11/05 12:22 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

