Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:hotelingpl
Spis treści
Hotelling T-kwadrat
Analiza Hotellinga zaproponowana została przez Hotellinga (1931)1) (1947)2) i Mahalanobisa (19303), 19364)) jest rozszerzeniem testów t-Studenta do dziedziny wielu zmiennych. W rezultacie jednoczesnej analizie możemy poddawać wiele różnych cech badanych obiektów.
Test T-kwadrat Hotellinga dla pojedynczej próby
Służy do weryfikacji hipotezy, że  zmiennych w badanej populacji
zmiennych w badanej populacji 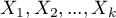 charakteryzuje się średnimi zadanymi przez badacza.
charakteryzuje się średnimi zadanymi przez badacza.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- wielowymiarowy rozkład normalny lub normalność rozkładu każdej badanej zmiennej.
Hipotezy:
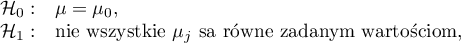
gdzie:
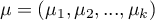 - średnie zmiennych w populacji reprezentowanej przez próbę,
- średnie zmiennych w populacji reprezentowanej przez próbę,
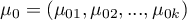 - zadane przez badacza wartości średnich.
- zadane przez badacza wartości średnich.
Statystyka testowa ma postać:
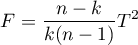
gdzie:
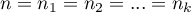 - liczności poszczególnych zmiennych w próbie,
- liczności poszczególnych zmiennych w próbie,
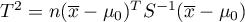 - pierwotna statystyka testowa Hotellinga o rozkładzie
- pierwotna statystyka testowa Hotellinga o rozkładzie  (zalecana dla prób o dużych licznościach),
(zalecana dla prób o dużych licznościach),
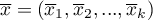 - średnie zmiennych w próbie,
- średnie zmiennych w próbie,
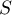 - macierz kowariancji.
- macierz kowariancji.
Statystyka ta podlega rozkładowi F Snedecora z  i
i 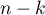 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Gdy po wykonanej analizie szukamy zmiennych, których dotyczą różnice, wyznaczamy jednoczesne przedziały ufności średnich:
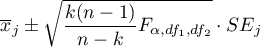
lub przedziały z poprawką Bonferroniego, w celu sprawdzenia czy znajduje się w nich zadana wartość. Jeśli bowiem zadana wartość znajduje się w wyznaczonym przedziale to oznacza, że w rzeczywistości średnia danej zmiennej może być równa tej zadanej wartości. Stosując tą metodę należy jednak pamiętać, że wyznaczone przedziały nie uwzględniają powiązań pomiędzy poszczególnymi zmiennymi (które uwzględnia test Hotellinga) a jedynie wielokrotne testowanie.
Szukając zmiennych, których dotyczą różnice możemy również zastosować podejście jednowymiarowe. Wykonujemy wówczas porównania testem t-Studenta dla pojedynczej próby oddzielnie dla poszczególnych zmiennych. Niestety, nie uwzględnimy tym samym wzajemnych powiązań, ale uzyskane wartości  testu t-Studenta możemy skorygować w dziale Wielokrotne porównania.
testu t-Studenta możemy skorygować w dziale Wielokrotne porównania.
Uwaga!
Zasada działania testu Hotellinga jest tożsama z budową „wielowymiarowej elipsy” przedziałów ufności wokół centrum wyznaczonego przez średnie. Przez co, stosując analizę jednowymiarową (nie uwzględniającą wzajemnych powiązań między zmiennymi) często nie jesteśmy w stanie uzyskać tożsamych wyników.
Przykład - interpretacja elipsy testu Hotellinga dla dwóch zmiennych
Zadany punkt opisany przez wartości średnie (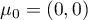 ) znajduje się poza elipsą, co oznacza, że test Hotellinga odrzuca hipotezę
) znajduje się poza elipsą, co oznacza, że test Hotellinga odrzuca hipotezę  , ale stosując podejście jednowymiarowe (przedziały ufności dla każdej zmiennej oddzielnie) nie jesteśmy w stanie odrzucić hipotezy
, ale stosując podejście jednowymiarowe (przedziały ufności dla każdej zmiennej oddzielnie) nie jesteśmy w stanie odrzucić hipotezy  , by wskazać zmienną, której dotyczą różnice.
, by wskazać zmienną, której dotyczą różnice.
(0.5,2)
\psline[linecolor=red]{<->}(1.5,-0.3)(1.5,3.25)
\psline[linecolor=red]{<->}(-1.6,-0.7)(0.55,-0.7)
\rput[b]{90}(1.7,1.4){\textcolor{red}{\psframebox*{\tiny $95\%CI (\mu_2)$}}}
\rput(-0.5,-0.7){\textcolor{red}{\psframebox*{\tiny $95\%CI (\mu_1)$}}}
\rput(-2,2.3){\scriptsize elipsa przedziału}
\rput(-2,2){\scriptsize ufności dla średnich}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgdf1b106bb83a542be98c4ca58398239d.png)
Okno z ustawieniami opcji testu Hotellinga dla pojedynczej próby wywołujemy poprzez menu Statystyka→Testy parametryczne→T-kwadrat Hotellinga
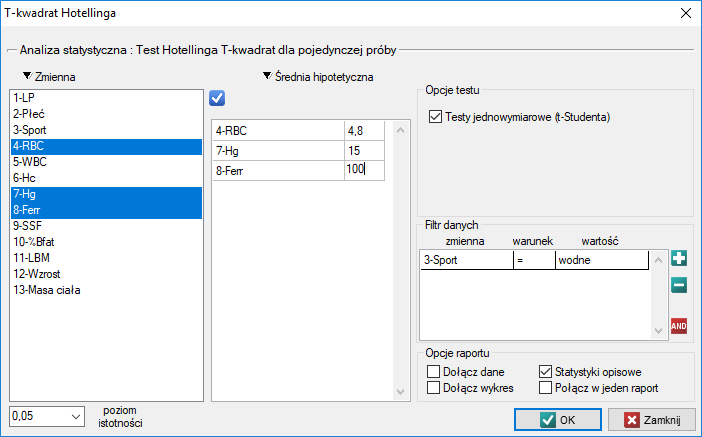
Przebadano grupę sportowców by uzyskać informację między innymi o takich parametrach zdrowotnych jak:
RBC - Liczba czerwonych krwinek,
Hg - Hemoglobina [g/dl],
Ferr - Ferrytyna [µg/l].
Chcemy wiedzieć, na ile bliskie oczekiwanym przez badaczy wartościom są średnie poziomy RBC, hemoglobiny i ferrytyny dla sportowców uprawiających tzw. sporty „wodne”. Oczekiwane średnie to:
RBC = 4.8,
Hg = 15[g/dl],
Ferr = 100[µg/l].
Hipotezy:

Ponieważ arkusz danych zawiera informacje o badanych parametrach dla większej grupy sportowców, w oknie analizy osoby, które uprawiają sporty wodne wskazujemy poprzez filtr danych.
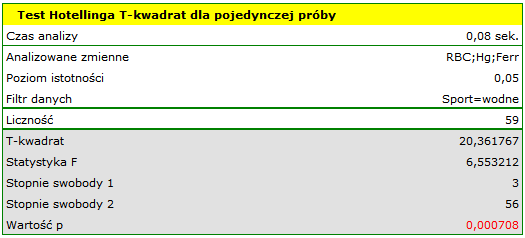
Porównując wartość 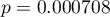 z poziomem istotności
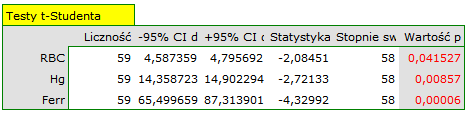
z poziomem istotności  stwierdzamy, że średnie poziomy badanych parametrów różnią się od wartości zadanej. Różnic możemy poszukiwać w wyznaczonych jednoczesnych przedziałach ufności lub w przedziałach z korektą Bonferroniego. Dla ferrytyny jednoczesny 95% przedział ufności znajduje się poniżej zadanej wartości, co świadczy o niższej populacyjnej wartości ferrytyny niż zadana przez badaczy. Przedział dla RBC i hemoglobiny zawiera zadane wartości, co wskazuje na brak istotnych statystycznie różnic.
stwierdzamy, że średnie poziomy badanych parametrów różnią się od wartości zadanej. Różnic możemy poszukiwać w wyznaczonych jednoczesnych przedziałach ufności lub w przedziałach z korektą Bonferroniego. Dla ferrytyny jednoczesny 95% przedział ufności znajduje się poniżej zadanej wartości, co świadczy o niższej populacyjnej wartości ferrytyny niż zadana przez badaczy. Przedział dla RBC i hemoglobiny zawiera zadane wartości, co wskazuje na brak istotnych statystycznie różnic.

Nieco węższe przedziały uzyskamy wykorzystując poprawkę Bonferroniego, wówczas nie tylko przedział dla ferrytyny znajduje się poniżej przedziału ufności ale również przedział dla hemoglobiny.

Podejście jednowymiarowe ze względu na swoją prostotę wykorzystywane jest najczęściej. Możemy tu wybrać mniej konserwatywne korekty wielokrotnych porównań niż poprawka Bonferroniego lub Sidaka, uzyskując w ten sposób różnice dotyczące wszystkich badanych parametrów.
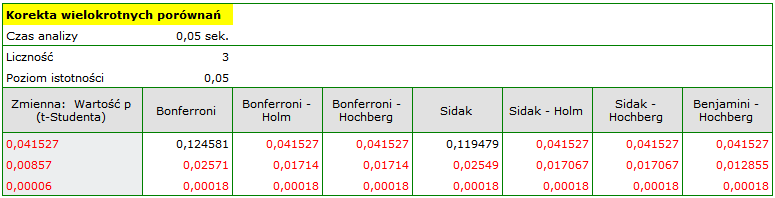
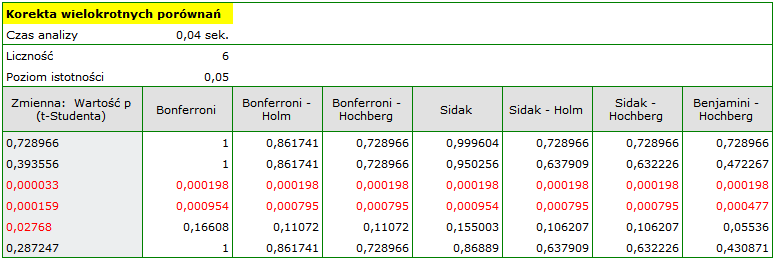
By wykonać korektę wartości  testu t-Studenta należy przekopiować te wartości do jednej kolumny nowego arkusza danych i z menu
testu t-Studenta należy przekopiować te wartości do jednej kolumny nowego arkusza danych i z menu Statystyka wybrać Korektę wielokrotnych porównań.
2014/12/17 22:24
· admin
Test T-kwadrat Hotellinga dla grup zależnych
Stosuje się w sytuacji gdy pomiarów badanych  zmiennych dokonujemy dwukrotnie w różnych warunkach (przy czym zakładamy, że wariancje zmiennych w obu pomiarach są sobie bliskie). Jeśli pierwszy pomiar oznaczymy przez
zmiennych dokonujemy dwukrotnie w różnych warunkach (przy czym zakładamy, że wariancje zmiennych w obu pomiarach są sobie bliskie). Jeśli pierwszy pomiar oznaczymy przez 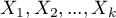 a drugi przez
a drugi przez 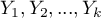 , wówczas weryfikujemy hipotezę że populacyjne średnie zmiennych z pierwszego pomiaru są takie same jak z pomiaru drugiego. Równoważnie gdy wyznaczymy różnice pomiędzy parami pomiarów
, wówczas weryfikujemy hipotezę że populacyjne średnie zmiennych z pierwszego pomiaru są takie same jak z pomiaru drugiego. Równoważnie gdy wyznaczymy różnice pomiędzy parami pomiarów 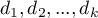 , hipoteza wskaże, że średnie dla różnic w badanej populacji wynoszą 0.
, hipoteza wskaże, że średnie dla różnic w badanej populacji wynoszą 0.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- wielowymiarowy rozkład normalny lub normalność rozkładu każdej badanej zmiennej,
Hipotezy:
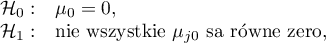
gdzie:
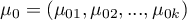 - populacyjne średnie różnic pomiaru pierwszego i drugiego.
- populacyjne średnie różnic pomiaru pierwszego i drugiego.
Statystyka testowa ma postać:
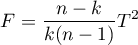
gdzie:
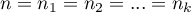 - liczności poszczególnych różnic w próbie,
- liczności poszczególnych różnic w próbie,
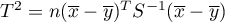 - pierwotna statystyka testowa Hotellinga o rozkładzie
- pierwotna statystyka testowa Hotellinga o rozkładzie  (zalecana dla prób o dużych licznościach),
(zalecana dla prób o dużych licznościach),
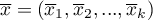 - średnie zmiennych w próbie dla pierwszego pomiaru,
- średnie zmiennych w próbie dla pierwszego pomiaru,
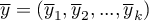 - średnie zmiennych w próbie dla drugiego pomiaru,
- średnie zmiennych w próbie dla drugiego pomiaru,
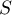 - macierz kowariancji różnic pomiaru pierwszego i drugiego.
- macierz kowariancji różnic pomiaru pierwszego i drugiego.
Statystyka ta podlega rozkładowi F Snedecora z  i
i 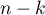 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Gdy po wykonanej analizie szukamy zmiennych, których dotyczą różnice, wyznaczamy jednoczesne przedziały ufności dla różnic średnich:
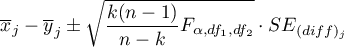
lub przedziały z poprawką Bonferroniego, w celu sprawdzenia czy znajduje się w nich wartość 0. Jeśli bowiem różnica może wynosić 0 to oznacza, że w rzeczywistości różnica pomiędzy badanymi wartościami może nie istnieć. Stosując tą metodę należy pamiętać, że wyznaczone przedziały nie uwzględniają powiązań pomiędzy zmiennymi towarzyszącymi (które uwzględnia test Hotellinga) a jedynie wielokrotne testowanie.
Szukając zmiennych, których dotyczą różnice możemy również zastosować podejście jednowymiarowe. Wykonujemy wówczas porównania testem t-Studenta dla grup zależnych oddzielnie dla poszczególnych zmiennych. Niestety, nie uwzględnimy tym samym wzajemnych powiązań, ale uzyskane wartości  testu
testu  -Studenta możemy skorygować w dziale Wielokrotne porównania.
-Studenta możemy skorygować w dziale Wielokrotne porównania.
Uwaga!
Zasada działania testu Hotellinga jest tożsama z budową „wielowymiarowej elipsy” przedziałów ufności wokół centrum wyznaczonego przez średnie różnic (patrz przykład interpretacji elipsy testu Hotellinga dla pojedynczej próby). Przez co, stosując analizę jednowymiarową (nie uwzględniającą wzajemnych powiązań między zmiennymi) często nie jesteśmy w stanie uzyskać tożsamych wyników.
Okno z ustawieniami opcji testu Hotellinga dla grup zależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→T-kwadrat Hotellinga dla grup zależnych
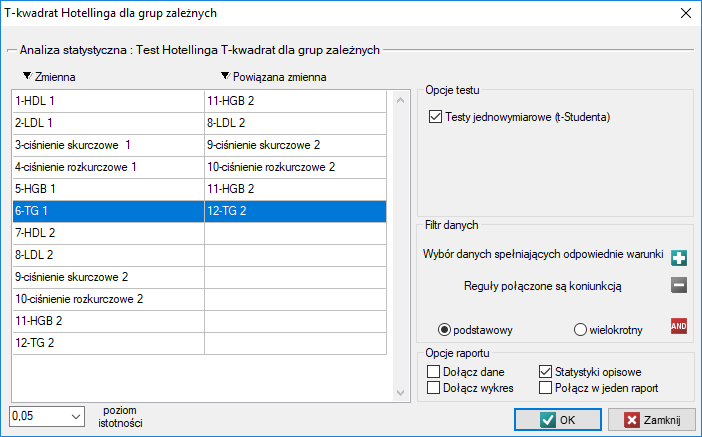
Przykład (plik nadcisnienie.pqs)
W grupie osób chorujących na nadciśnienie badano wpływ zastosowanego leczenia na zmiany wskaźników takich jak: cholesterol we frakcji HDL i LDL, hemoglobinę (HGB), trójglicerydy (TG) oraz wartości ciśnienia skurczowego i rozkurczowego krwi. Pomiary od 44 pacjentów pobrano dwukrotnie (przed leczeniem i po 3 miesiącach stosowania leczenia). Następnie porównano uzyskane wyniki.
Hipotezy:
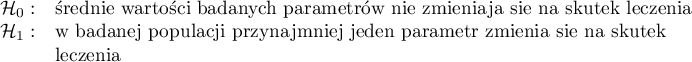

Porównując wartość 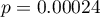 z poziomem istotności
z poziomem istotności  stwierdzamy, że średnie wartości badanych parametrów nie pozostają na tym samym poziomie (ich różnica jest istotnie różna od 0). Przedziały ufności dla ciśnienia skurczowego oraz rozkurczowego znajdują się powyżej wartości 0, co świadczy o istotnym obniżeniu tych parametrów na skutek leczenia. Przedziały dla pozostałych parametrów zawierają wartość 0, a więc nie mamy dowodów na ich zmianę na skutek leczenia.
stwierdzamy, że średnie wartości badanych parametrów nie pozostają na tym samym poziomie (ich różnica jest istotnie różna od 0). Przedziały ufności dla ciśnienia skurczowego oraz rozkurczowego znajdują się powyżej wartości 0, co świadczy o istotnym obniżeniu tych parametrów na skutek leczenia. Przedziały dla pozostałych parametrów zawierają wartość 0, a więc nie mamy dowodów na ich zmianę na skutek leczenia.
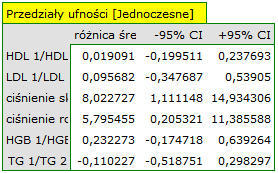
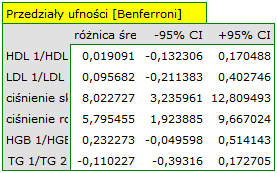
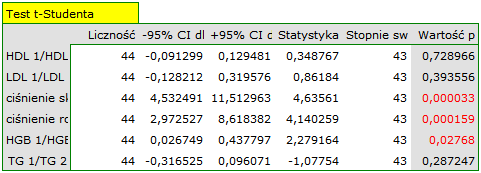
Podejście jednowymiarowe ze względu na swoją prostotę wykorzystywane jest najczęściej. Stosując to podejście wraz z korektą wielokrotnych porównań również uznamy, że różnice dotyczą jedynie wartości ciśnienia.
By wykonać korektę wartości  testu t-Studenta należy przekopiować te wartości do jednej kolumny nowego arkusza danych i z menu
testu t-Studenta należy przekopiować te wartości do jednej kolumny nowego arkusza danych i z menu Statystyka wybrać Korektę wielokrotnych porównań.
2014/12/17 22:37
· admin
Test T-kwadrat Hotellinga dla grup niezależnych
Służy do weryfikacji hipotezy o równości średnich badanych  zmiennych
zmiennych 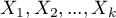 z populacji pierwszej i średnich tych samych
z populacji pierwszej i średnich tych samych  zmiennych
zmiennych 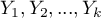 z populacji drugiej.
z populacji drugiej.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- wielowymiarowy rozkład normalny w obu populacjach lub normalność rozkładu każdej badanej zmiennej w obu populacjach,
- równość wariancji badanych zmiennych obu populacji lub równość macierzy kowariancji - warunek szczególnie istotny w przypadku grup o różnych licznościach - gdy warunek nie jest pełniony, powinna zostać wyznaczona korekta.
Hipotezy:
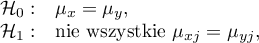
gdzie:
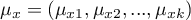 - średnie zmiennych w populacji pierwszej,
- średnie zmiennych w populacji pierwszej,
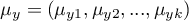 - średnie zmiennych w populacji drugiej.
- średnie zmiennych w populacji drugiej.
Statystyka testowa ma postać:
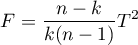
gdzie:
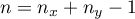 ,
,
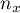 ,
, 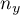 - liczności pierwszej i drugiej próby (liczności poszczególnych zmiennych takie same) ,
- liczności pierwszej i drugiej próby (liczności poszczególnych zmiennych takie same) ,
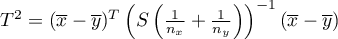 - pierwotna statystyka testowa Hotellinga o rozkładzie
- pierwotna statystyka testowa Hotellinga o rozkładzie  (zalecana dla prób o dużych licznościach),
(zalecana dla prób o dużych licznościach),
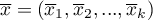 - średnie zmiennych w próbie pierwszej,
- średnie zmiennych w próbie pierwszej,
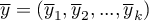 - średnie zmiennych w próbie drugiej,
- średnie zmiennych w próbie drugiej,
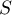 - macierz kowariancji wspólna (ang. pooled) dla obu prób.
- macierz kowariancji wspólna (ang. pooled) dla obu prób.
Statystyka ta podlega rozkładowi F Snedecora z  i
i 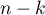 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Gdy po wykonanej analizie szukamy zmiennych, których dotyczą różnice, wyznaczamy jednoczesne przedziały ufności dla różnic średnich
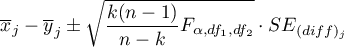
lub przedziały z poprawką Bonferroniego, w celu sprawdzenia czy znajduje się w nich wartość 0. Jeśli bowiem różnica może wynosić 0 to oznacza, że w rzeczywistości różnica pomiędzy badanymi wartościami może nie istnieć. Stosując tą metodę należy pamiętać, że wyznaczone przedziały nie uwzględniają powiązań pomiędzy zmiennymi (które uwzględnia test Hotellinga) a jedynie wielokrotne testowanie.
Szukając zmiennych, których dotyczą różnice możemy również zastosować podejście jednowymiarowe. Wykonujemy wówczas porównania testem t-Studenta dla grup niezależnych oddzielnie dla poszczególnych zmiennych. Niestety, nie uwzględnimy tym samym wzajemnych powiązań, ale uzyskane wartości  testu
testu  -Studenta możemy skorygować w dziale Wielokrotne porównania.
-Studenta możemy skorygować w dziale Wielokrotne porównania.
Uwaga!
Zasada działania testu Hotellinga jest tożsama z budową „wielowymiarowych elips” przedziałów ufności wokół centrów wyznaczonych przez średnie (patrz przykład interpretacji elipsy testu Hotellinga dla pojedynczej próby). Przez co, stosując analizę jednowymiarową (nie uwzględniającą wzajemnych powiązań między zmiennymi) często nie jesteśmy w stanie uzyskać tożsamych wyników.
Okno z ustawieniami opcji testu Hotellinga dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→T-kwadrat Hotellinga dla grup niezależnych.
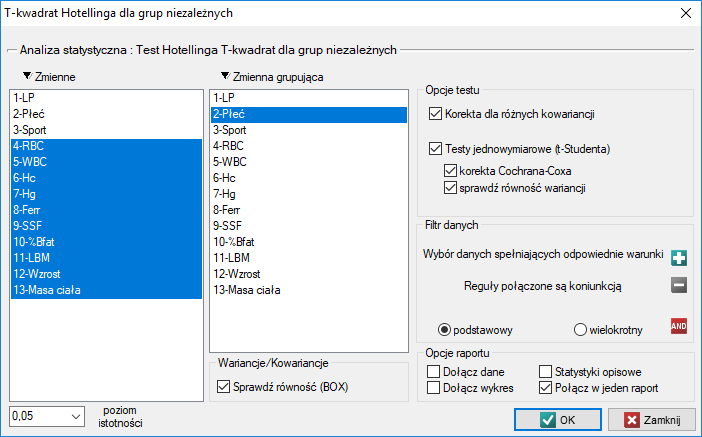
Przykład c.d. (plik sport.pqs)
2014/12/17 22:41
· admin
Test T-kwadrat Hotellinga dla grup niezależnych z korektą dla różnych wariancji
Poprawka dotyczy testu T-kwadrat Hotellinga dla grup niezależnych i jest wyliczana wówczas, gdy wariancje badanych zmiennych w obu populacjach są różne.
Statystyka testowa ma postać:
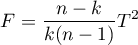
gdzie:
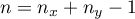 ,
,
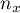 ,
, 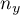 - liczności pierwszej i drugiej próby (liczności poszczególnych zmiennych równe) ,
- liczności pierwszej i drugiej próby (liczności poszczególnych zmiennych równe) ,
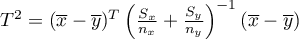 - pierwotna statystyka testowa Hotellinga o rozkładzie
- pierwotna statystyka testowa Hotellinga o rozkładzie  (zalecana dla prób o dużych licznościach),
(zalecana dla prób o dużych licznościach),
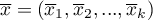 - średnie zmiennych w próbie pierwszej,
- średnie zmiennych w próbie pierwszej,
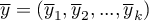 - średnie zmiennych w próbie drugiej,
- średnie zmiennych w próbie drugiej,
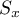 ,
, 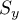 - macierz kowariancji dla pierwszej i drugiej próby.
- macierz kowariancji dla pierwszej i drugiej próby.
Statystyka ta podlega rozkładowi F Snedecora z  i
i 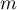 stopniami swobody (gdzie
stopniami swobody (gdzie 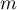 to liczba stopni swobody skorygowana ze względu na różne wariancje).
to liczba stopni swobody skorygowana ze względu na różne wariancje).
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Gdy po wykonanej analizie szukamy zmiennych, których dotyczą różnice, wyznaczamy jednoczesne przedziały ufności dla różnic średnich
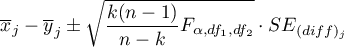
lub przedziały z poprawką Bonferroniego, w celu sprawdzenia czy znajduje się w nich wartość 0. Jeśli bowiem różnica może wynosić 0 to oznacza, że w rzeczywistości różnica pomiędzy badanymi wartościami może nie istnieć. Stosując tą metodę należy pamiętać, że wyznaczone przedziały nie uwzględniają powiązań pomiędzy zmiennymi (które uwzględnia test Hotellinga) a jedynie wielokrotne testowanie.
Szukając zmiennych, których dotyczą różnice możemy również zastosować podejście jednowymiarowe. Wykonujemy wówczas porównania testem t-Studenta z korektą Cochrana-Coxa oddzielnie dla poszczególnych zmiennych. Niestety, nie uwzględnimy tym samym wzajemnych powiązań, ale uzyskane wartości  testu
testu  -Studenta możemy skorygować w dziale Wielokrotne porównania.
-Studenta możemy skorygować w dziale Wielokrotne porównania.
Uwaga!
Zasada działania testu Hotellinga jest tożsama z budową „wielowymiarowych elips” przedziałów ufności wokół centrów wyznaczonych przez średnie (patrz przykład interpretacji elipsy testu Hotellinga dla pojedynczej próby). Przez co, stosując analizę jednowymiarową (nie uwzględniającą wzajemnych powiązań między zmiennymi) często nie jesteśmy w stanie uzyskać tożsamych wyników.
Okno z ustawieniami opcji testu Hotellinga dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→T-kwadrat Hotellinga dla grup niezależnych.

Przebadano grupę sportowców by uzyskać informację o parametrach zdrowotnych takich jak:
![LaTeX \begin{tabular}{ll}
RBC - Liczba czerwonych krwinek, & SSF - Suma fałdów skórno-tłuszczowych [mm],\\
WBC - Liczba białych krwinek, & \% Bfat - Zawartość tłuszczu w organizmie,\\
Hc - Hematokryt [\%], & LBM - Beztłuszczowa masa ciała [kg],\\
Hg - Hemoglobina [g/dl], & Wzrost [cm],\\
Ferr - Ferrytyna [µg/l], & Masa ciała [kg].
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img5ad8771ed09589cf5bd45a6e79dcdc36.png)
Chcemy wiedzieć, czy kobiety i mężczyźni, uprawiający zawodowo analizowane rodzaje sportu, różnią się poziomami tych parametrów.
Hipotezy:

Ze względu na różnice dotyczące kowariancji analizowanych parametrów (wartość  testu Boxa
testu Boxa 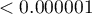 ) analizę przeprowadzamy przy włączonej korekcie różnych macierzy kowariancji.
) analizę przeprowadzamy przy włączonej korekcie różnych macierzy kowariancji.

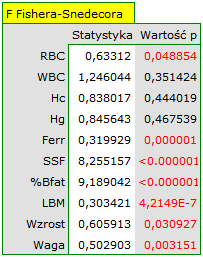
Uzyskany wynik skorygowanej statystyki Hotellinga jest przedstawiony poniżej.
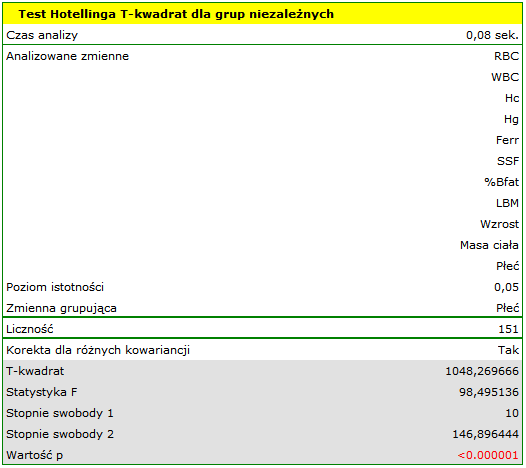
Porównując wartość 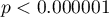 z poziomem istotności
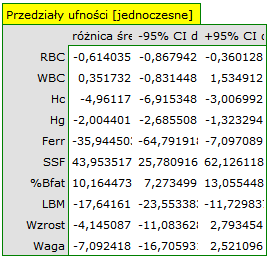
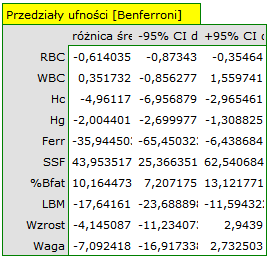
z poziomem istotności  stwierdzamy, że mężczyźni i kobiety w badanej populacji mają inne wartości średnie analizowanych parametrów. Według jednoczesnych przedziałów ufności (oraz według przedziałów z korektą Bonferroniego) różnice dotyczą:
stwierdzamy, że mężczyźni i kobiety w badanej populacji mają inne wartości średnie analizowanych parametrów. Według jednoczesnych przedziałów ufności (oraz według przedziałów z korektą Bonferroniego) różnice dotyczą:
RBC - średnio kobiety uzyskują niższe wartości,
Hc - średnio kobiety uzyskują niższe wartości,
Hg - średnio kobiety uzyskują niższe wartości,
Ferr - średnio kobiety uzyskują niższe wartości,
SSF - średnio mężczyźni uzyskują niższe wartości,
% Bfat - średnio mężczyźni uzyskują niższe wartości,
LBM - średnio kobiety uzyskują niższe wartości.
Pozostałe parametry czyli WBC, wzrost i masa ciała nie różnią się istotnie.
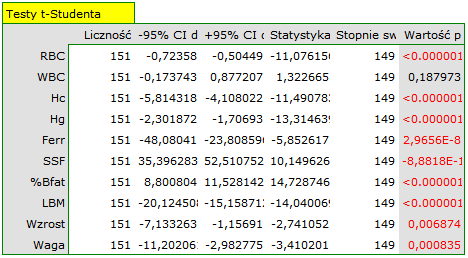
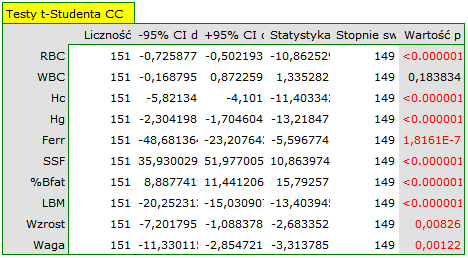
Podejście jednowymiarowe, choć nie uwzględniające wielokrotnego testowania ani wzajemnych powiązań, ze względu na swoją prostotę wykorzystywane jest najczęściej. Jego wyniki wskazują że różnice dotyczą wszystkich badanych parametrów za wyjątkiem WBC. Przy czym wyniki testu t-Studenta interpretujemy po uwzględnieniu korekty Cochrana-Coxa lub bez tej korekty, w zależności od spełnienia założenia równości wariancji (wynik testu Fishera-Snedecora). Chcąc uwzględnić wielokrotne testowania należałoby w tym przypadku zastosować jedną z korekt wartości p, opisanych w dziale Wielokrotne porównania.
2014/12/17 22:51
· admin
Test Box'a równości macierzy kowariancji
Test ten służy do porównania dwóch lub więcej ( ) macierzy kowariancji opisujących niezależne populacje.
) macierzy kowariancji opisujących niezależne populacje.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- wielowymiarowy rozkład normalny w badanych populacjach lub normalność rozkładu każdej badanej zmiennej w każdej populacji,
Hipotezy:
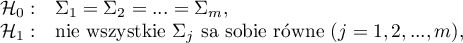
gdzie:
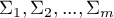 - populacyjne macierze kowariancji.
- populacyjne macierze kowariancji.
Statystyka testowa ma postać:
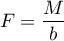
gdzie:
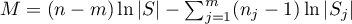 ,
,
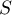 - wspólna (ang. pooled) macierz kowariancji,
- wspólna (ang. pooled) macierz kowariancji,
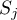 - macierz kowariancji dla
- macierz kowariancji dla  -tej próby,
-tej próby,
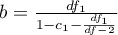 ,
,
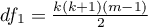 ,
,
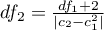 ,
,
 - liczba analizowanych zmiennych,
- liczba analizowanych zmiennych,
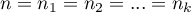 - liczności poszczególnych zmiennych w próbie.
- liczności poszczególnych zmiennych w próbie.
Statystyka ta podlega rozkładowi F Snedecora z 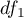 i
i 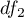 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Należy pamiętać, że test Box'a jest szczególnie wrażliwy na złamanie założenia normalności rozkładu.
Test Box'a jest wyliczany opcjonalnie w Hotellingu dla grup niezależnych lub w analizie MANOVA.
Przykład c.d. (plik sport.pqs)
2014/12/17 22:57
· admin
1)
Hotelling H. (1931), The generalization of Student's ratio. Annals of Mathematical Statistics 2 (3): 360–378
2)
Hotelling, H. (1947), Multivariate Quality Control. In C. Eisenhart, M. W. Hastay, and W. A. Wallis, eds. Techniques of Statistical Analysis. New York: McGraw-Hill
3)
Mahalanobis P. C. (1930), On tests and measures of group divergence. Journal of the Asiatic Society of Bengal 26: 541–588
4)
Mahalanobis P. C. (1936), On the generalized distance in statistics. National Institute of Science of India 12: 49–55
statpqpl/hotelingpl.txt · ostatnio zmienione: 2019/12/17 17:29 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

