Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:manovapl
Spis treści
Jednoczynnikowa MANOVA
Jednoczynnikowa MANOVA
Wcześniej zalecamy zapoznanie się z analizą T-kwadrat Hotelling'a.
Jednoczynnikowa MANOVA (ang. multivariate analysis of variance), jest rozszerzeniem jednoczynnikowej ANOVA dla grup niezależnych. Służy do weryfikacji hipotezy o równości średnich badanych  zmiennych w kilku (
zmiennych w kilku ( ) populacjach.
) populacjach.
Pozostanie przy metodzie ANOVA polega na wielokrotnym (oddzielnie dla każdej zmiennej) porównaniu ( ) populacji, nie uwzględniając wzajemnego skorelowania zmiennych. Analiza typu MANOVA natomiast bada różnice pomiędzy populacjami jednoczenie dla wielu zmiennych, uwzględniając przy tym ich skorelowanie. Ponadto podejście MANOVA jest stosowane jako alternatywa dla ANOVA dla grup zależnych, gdyż nie wymaga spełnienia założenia sferyczności.
) populacji, nie uwzględniając wzajemnego skorelowania zmiennych. Analiza typu MANOVA natomiast bada różnice pomiędzy populacjami jednoczenie dla wielu zmiennych, uwzględniając przy tym ich skorelowanie. Ponadto podejście MANOVA jest stosowane jako alternatywa dla ANOVA dla grup zależnych, gdyż nie wymaga spełnienia założenia sferyczności.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- wielowymiarowy rozkład normalny w każdej populacji lub normalność rozkładu każdej badanej zmiennej w każdej populacji,
- równość macierzy kowariancji lub równość wariancji badanych zmiennych dla porównywanych populacji - warunek szczególnie istotny w przypadku grup o różnych licznościach.
Hipotezy:
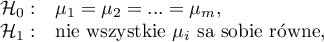
gdzie:
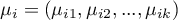 - średnie zmiennych w
- średnie zmiennych w  -tej populacji,
-tej populacji,
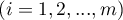 ,
,
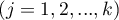 .
.
W analizach MANOVA posługujemy się kilkoma współczynnikami. Najszerzej znanym jest Lambda Wilksa. Ślad Pillai-Bartlett jest najbardziej konserwatywny, ale stosunkowo odporny w przypadku naruszenia założeń stosowania MANOVA i preferowany przy mało licznych próbach. Ślad Hotelling-Lawley natomiast jest najmniej konserwatywnym z trzech zaproponowanych testów. Pionierskie prace nad rozwojem tych technik rozpoczęli: Wilks (1932)1), Pillai(1955)2), Lawley(1938)3), Hotelling(1951)4), i Roy(1939)5).
Statystyki testowe bazują ma macierzach sum kwadratów i iloczynów mieszanych (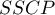 - ang. Sums of Squares and Cross Products). Macierz całkowita
- ang. Sums of Squares and Cross Products). Macierz całkowita 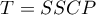 zostaje rozbita na dwie macierze, z których pierwsza związana jest z analizowaną hipotezą i oznaczana przez
zostaje rozbita na dwie macierze, z których pierwsza związana jest z analizowaną hipotezą i oznaczana przez 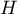 (w tym przypadku jest to macierz międzygrupowych sum kwadratów i iloczynów mieszanych), a druga dotyczy reszt (błędów) i jest oznaczana prze
(w tym przypadku jest to macierz międzygrupowych sum kwadratów i iloczynów mieszanych), a druga dotyczy reszt (błędów) i jest oznaczana prze 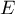 (macierz wewnątrzgrupowych sum kwadratów i iloczynów mieszanych).
(macierz wewnątrzgrupowych sum kwadratów i iloczynów mieszanych).
Lambda Wilksa
Wartość Lambdy definiowana jest następująco:
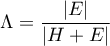
Statystyka testowa ma postać:
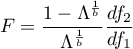
gdzie:
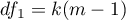 ,
, 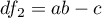 ,
,
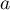 ,
,  ,
,  - współczynniki zależne od liczby analizowanych zmiennych i liczby porównywanych populacji.
- współczynniki zależne od liczby analizowanych zmiennych i liczby porównywanych populacji.
Ślad Hotelling-Lawley
Ślad Hotelling-Lawley definiowany jest następująco:
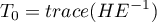
Statystyka testowa ma postać:
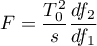
gdzie:
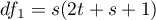 ,
, 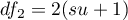 ,
,
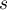 ,
,  ,
, 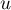 - współczynniki zależne od liczby analizowanych zmiennych i liczby porównywanych populacji.
- współczynniki zależne od liczby analizowanych zmiennych i liczby porównywanych populacji.
Ślad Pillai-Bartlett
Ślad Pillai-Bartlett definiowany jest następująco:
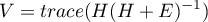
Statystyka testowa ma postać:
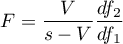
gdzie:
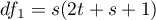 ,
, 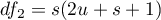 ,
,
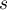 ,
,  ,
, 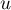 - współczynniki zależne od liczby analizowanych zmiennych i liczby porównywanych populacji.
- współczynniki zależne od liczby analizowanych zmiennych i liczby porównywanych populacji.
Każda z powyższych statystyk testowych podlega rozkładowi F Snedecora z 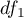 i
i 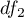 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Wielkość efektu - cząstkowa 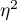
Wielkość ta określa proporcję wariancji wyjaśnionej do wariancji całkowitej związanej z danym czynnikiem. W modelu jednoczynnikowej MANOVA dla grup niezależnych wskazuje jaka część wewnątrzosobowej zmienności wyników może być przypisana badanemu czynnikowi wyznaczającemu grupy niezależne.
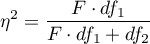
Wielkość efektu - kontrasty, analiza jednowymiarowa
Gdy wykonywana analiza ma porównać wybrane populacje, lub wybrany układ populacji, wówczas przeprowadzamy analizę kontrastów. Analiza ta jest analogiczna do kontrastów w analizie jednowymiarowej ale uwzględnia wzajemne powiązanie zmiennych.
Dla wielkości efektu można także wyznaczyć jednoczesne przedziały ufności lub przedziały ufności z poprawką Bonferroniego. Stosując te przedziały należy jednak pamiętać, że nie uwzględniają one powiązań pomiędzy poszczególnymi zmiennymi (które uwzględnia MANOVA) a jedynie wielokrotne testowanie.
Szukając zmiennych, których dotyczą różnice, możemy również zastosować podejście jednowymiarowe. Wykonujemy wówczas porównania ANOVA dla grup niezależnych oddzielnie dla poszczególnych zmiennych. Niestety, nie uwzględnimy tym samym wzajemnych powiązań, ale uzyskane na podstawie ANOVA wartości  możemy skorygować w dziale Wielokrotne porównania.
możemy skorygować w dziale Wielokrotne porównania.
Uwaga!
Zasada działania MANOVA (podobnie jak testów Hotellinga) jest tożsama z budową „wielowymiarowych elips” przedziałów ufności wokół centrów wyznaczonych przez średnie (patrz przykład interpretacji elipsy testu Hotellinga dla pojedynczej próby). Przez co, stosując analizę jednowymiarową (nie uwzględniającą wzajemnych powiązań między zmiennymi) często nie jesteśmy w stanie uzyskać tożsamych wyników.
Okno z ustawieniami opcji MANOVA dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→Jednoczynnikowa MANOVA dla grup niezależnych
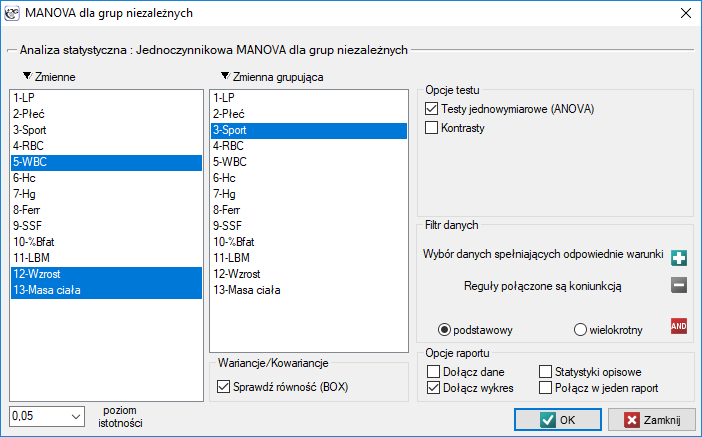
Przebadano grupę sportowców by uzyskać informację o parametrach zdrowotnych m.in. takich jak:
WBC - Liczba białych krwinek,
Wzrost [cm],
Masa ciała [kg].
Chcemy wiedzieć:
- czy uprawiający zawodowo trzy rodzaje sportów: „gry zespołowe” (jak: koszykówka, siatkówka, itp.) „bieżnia” (jak: 100m, 400m, itp.) „wodne” (jak: pływanie, wioślarstwo, itp.), różnią się poziomami tych parametrów.
- czy uprawiający sporty wymagające dużego wysiłku takie jak: „bieżnia” i „wodne” różnią się poziomami tych parametrów od uprawiających „gry zespołowe”
Ad.1)
Hipotezy:

Wynik testu Box'a (p=0.63025) pozwala na wyliczenie Analiz typu MANOVA.
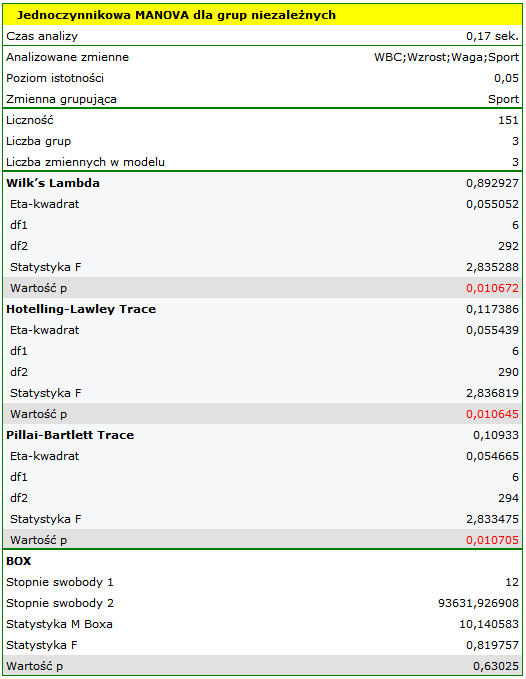
Istotność współczynników: Lambda Wilksa, śladu Hotelling-Lawley oraz śladu Pillai-Bartlett pozwala twierdzić, że badane populacje sportowców różnią się co do tych parametrów. By określić różnice przeprowadzamy analizę jednowymiarową ANOVA.
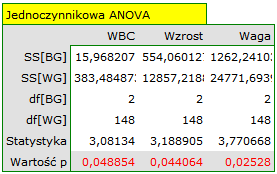
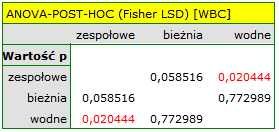
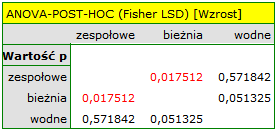
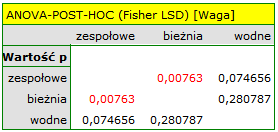
Do uzyskanych wyników należy podejść ostrożnie. Choć wskazują one na istotne różnice we wszystkich porównywanych parametrach, zwracają wartość p na pograniczu istotności statystycznej (dla WBC p=0.04885, dla wzrostu p=0.04406, dla wagi p=0.02528). Dodatkowo przy ich interpretacji należy pamiętać, że nie uwzględniają one ani wzajemnego skorelowania parametrów, ani wielokrotnego testowania. Uwzględnienie wielokrotnego testowania wymagałoby w tym przypadku zastosowania jednej z korekt wartości p, opisanych w dziale Wielokrotne porównania.
Ad.2)
Hipotezy:

By sprawdzić prawdziwość powyższych hipotez, w oknie analizy ustawiamy odpowiedni kontrast. Jako wartość kontrastu wpisujemy 2 dla sportów zespołowych, -1 dla bieżni i dyscyplin określanych jako wodne.
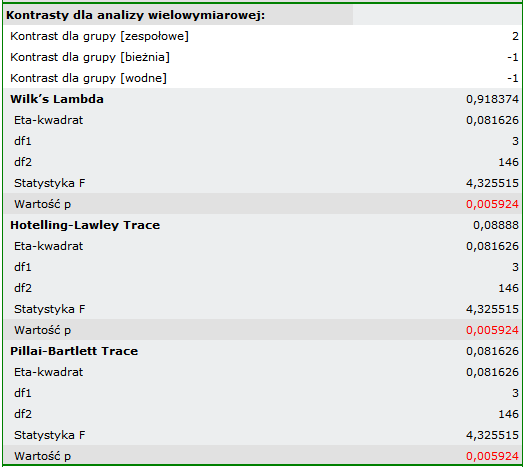
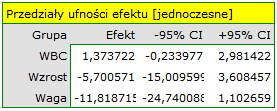
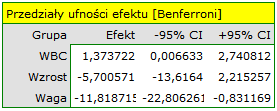
W rezultacie uzyskana istotność współczynników: Lambda Wilksa, śladu Hotelling-Lawley oraz śladu Pillai-Bartlett (p=0.00592) pozwala twierdzić, że sportowcy uprawiający sporty wymagające dużego wysiłku różnią się co do tych parametrów od uprawiających gry zespołowe. W przedziałach jednoczesnych nie obserwujemy tych różnic, natomiast na bazie przedziałów Bonferroniego możemy stwierdzić, że różnica dotyczy wagi i WBC. Wartości WBC są wyższe w grupie sportów zespołowych, a masa ciała jest istotnie niższa w tej grupie.
2014/12/18 23:09
· admin
1)
Wilks S.S. (1932), Certain generalizations in the analysis of variance. Biometrika 24: 471–494
2)
Pillai K. C. (1955), Some new test criteria in multivariate analysis. Annals of Mathematical Statistics 26: 117–121
3)
Lawley D. N. (1938), A generalization of Fisher’s z-test.
Biometrika 30: 180–187.
4)
Hotelling H. (1951), A generalized t 2 test and measurement of multivariate dispersion. Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability 1: 23–41
5)
Roy S. N. (1939), p-statistics or some generalizations in analysis of variance appropriate to multivariate problems. Sankhya 4: 381–396
statpqpl/manovapl.txt · ostatnio zmienione: 2015/05/04 13:34 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

