Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:wielowympl
Spis treści
Modele wielowymiarowe
Wielowymiarowe modele regresji dają możliwość badania wpływu wielu zmiennych niezależnych (wielu czynników) oraz ich interakcji na jedną zmienną zależną. Poprzez modele wielowymiarowe możliwe jest również budowanie jednocześnie wielu uproszczonych modeli - modeli jednowymiarowych (jednoczynnikowych). Informacja o tym, jaki model chcemy budować (wieloczynnikowy czy jednoczynnikowy) widoczna jest w oknie wybranej analizy. Przy jednoczesnym wyborze wielu zmiennych niezależnych w oknie analizy możliwe jest dokonanie wyboru modelu.
Przygotowanie zmiennych do analizy
Dopasowanie grup
Dlaczego dokonuje się dopasowania grup?
Odpowiedzi na to pytanie jest bardzo wiele. Posłużymy się przykładem sytuacji medycznych.
Jeśli szacujemy efekt leczenia na podstawie eksperymentu z pełną randomizacją, to przypisując losowo osoby do grupy leczonej i nieleczonej tworzymy grupy podobne pod względem możliwych czynników zakłócających. Podobieństwo grup wynika z samego losowego przydziału. W takich badaniach możemy badać czysty (niezależny od czynników zakłócających) wpływ metody leczenia na wynik eksperymentu. W takim przypadku inne poza losowym dopasowanie grup nie jest konieczne.
Możliwość błędu pojawia się, gdy różnica w wyniku leczenia między leczonymi i nieleczonymi grupami może być spowodowana nie przez samo leczenie, ale przez czynnik, który skłonił do wzięcia udziału w leczeniu. Dzieje się tak wtedy, gdy z pewnych względów randomizacja nie jest możliwa, np. jest to badanie obserwacyjne lub ze względów etycznych nie możemy przypisać leczenia dowolnie. Wówczas sztuczne dopasowanie grup może mieć zastosowanie. Na przykład jeśli osoby które przydzielamy do grupy leczonej to osoby zdrowsze, a osoby które są w grupie kontrolnej to osoby o większym nasileniu choroby, wówczas to nie sam sposób leczenia, ale stan pacjenta przed leczeniem może mieć wpływ na wynik eksperymentu. Gdy zobaczymy taką nierównowagę grup, dobrze jest, kiedy możemy zdecydować się na randomizację, w ten sposób problem zostaje rozwiązany, gdyż losowanie osób do grup powoduje, że stają się one podobne. Można sobie jednak wyobrazić inną sytuację. Tym razem grupą, którą jesteśmy zainteresowani nie będą osoby poddane leczeniu lecz osoby palące, a grupą kontrolną osoby niepalące, a analizy będą miały na celu wykazanie niekorzystnego wpływu palenia na występowanie raka płuc. Wówczas, chcąc sprawdzić czy palenie rzeczywiście wpływa na zwiększenie ryzyka zachorowania, byłoby nieetycznym wykonanie badania z pełną randomizacją, ponieważ oznaczałoby ono, że losowo wybrane do grupy ryzyka osoby zmusimy do palenia. Rozwiązaniem tej sytuacji jest ustalenie grupy narażonej, czyli wylosowanie pewnej liczby osób spośród osób które już palą, a następnie dobór grupy kontrolnej złożonej z niepalących. Grupa kontrolna powinna być dobrana, ponieważ zostawiając dobór przypadkowi możemy uzyskać grupę niepalącą, która jest młodsza od palących tylko ze względu na fakt, że w naszym kraju palenie staje się mniej modne, a więc automatycznie wśród osób niepalących jest wiele osób młodych. Kontrolna powinna być wylosowana z osób niepalących, ale tak, by była jak najbardziej podobna do grupy leczonej. W ten sposób przybliżamy się do badania czystego (niezależnego od wybranych czynników zakłócających takich jak chociażby wiek) wpływu palenia/nie palenia na wynik eksperymentu czyli w tym przypadku wystąpienie nowotworu płuc. Taki dobór możemy wykonać właśnie poprzez zaproponowane w programie dopasowanie.
Jedną z głównych zalet kontrolowanego przez badacza dopasowania jest upodobnienie się grupy kontrolnej do grupy leczonej, ale jest to też największa wada tej metody. Jest to zaleta, ponieważ nasze badanie coraz bardziej przypomina badanie randomizowane. W badaniu randomizowanym grupa bada i kontrolna jest podobna pod względem niemalże wszystkich cech, również tych których nie badamy – losowy podział zapewnia nam to podobieństwo. W wyniku zastosowania dopasowania kontrolowanego przez badacza grupa leczona i kontrolna stają się podobne pod względem tylko wybranych cech.
Sposoby oceny podobieństwa:
Dwa pierwsze wymienione sposoby opierają się na dopasowaniu grup poprzez dopasowanie wyników skłonności (ang. Propensity Score Matching, PSM). Ten rodzaj dopasowania został zaproponowany przez Rosenbauma i Rubina 1). W praktyce jest to technika doboru grupy kontrolnej (osób nie leczonych lub leczonych minimalnie/standardowo) do grupy leczonej na podstawie prawdopodobieństwa opisującego skłonność badanych do przypisania leczenia w zależności od obserwowanych zmiennych towarzyszących. Wynik prawdopodobieństwa opisującego skłonności, z angielskiego nazywany Propensity Score jest wynikiem równoważącym, dlatego w wyniku doboru grupy kontrolnej do grupy leczonej rozkład zmierzonych zmiennych towarzyszących staje się bardziej podobny między osobami leczonymi i nieleczonymi. Trzecia metoda nie wyznacza prawdopodobieństwa dla każdej osoby, ale wyznacza macierz odległości/niepodobieństwa, która wskazuje obiekty najbliższe/najbardziej podobne pod względem wielu wybranych cech.
Metody:
- Zadane prawdopodobieństwo – czyli podaną dla każdej badanej osoby wartość z przedziału od 0 do 1, określającą prawdopodobieństwo przynależenia do grupy leczonej czyli Propensity Score. Takie prawdopodobieństwo może zostać wyznaczone wcześniej różnymi metodami. Na przykład w modelu regresji logistycznej, poprzez sieci neuronowe lub wiele innych metod. Jeśli osoba z grupy, z której losujemy kontrole uzyska Propensity Score podobne do tego jaki uzyskała osoba z grupy leczonej, wówczas może ona wejść do analizy, ponieważ obie te osoby są podobne pod względem cech, jakie były rozważane przy wyznaczaniu Propensity Score.
- Wyznaczone z modelu regresji logistycznej – ponieważ regresja logistyczna to najczęściej stosowana metoda doboru, program PQStat daje możliwość wyznaczenia automatycznie w oknie analizy wartości Propensity Score w oparciu o tę metodę. Dopasowanie przebiega dalej przy wykorzystaniu uzyskanego w ten sposób Propensity Score.
- Macierz podobieństwa/odległości – na podstawie tej opcji nie jest wyznaczana wartość Propensity Score, ale budowana jest macierz wskazująca odległość każdej osoby z grupy leczonej do osoby z grupy kontrolnej. Użytkownik może zadać warunki brzegowe np. może wskazać, że osoba dobrana do danej osoby z grupy badanej nie może się od niej różnic wiekiem bardziej niż o 3 lata i musi być tej samej płci. Odległości w budowanej macierzy wyznaczone są w oparciu o dowolną metrykę lub sposób opisujący niepodobieństwo. Ten sposób doboru grupy kontrolnej do leczonej jest bardzo elastyczny. Oprócz dowolnego wyboru sposobu wyznaczania odległości/niepodobieństwa, w wielu metrykach pozwala na wskazywanie wag określających to, jak ważne są dla badacza poszczególne zmienne, tzn. na podobieństwie jednych zmiennych może badaczowi zależeć bardziej, podczas gdy podobieństwo innych jest mniej ważne. Jednak w przypadku wyboru macierzy odległości/niepodobieństwa zalecana jest duża ostrożność. Wiele cech i wiele soposobów wyznaczania odległości wymaga wcześniejszego standaryzowania lub normalizowania danych, ponadto wybór odwrotności odległości lub podobieństwa (zamiast niepodobieństwa) może skutkować wyszukiwaniem najbardziej odległych i niepodobnych obiektów, podczas gdy standardowo stosujemy te metody do wyszukiwania obiektów podobnych. Jeśli badacz nie ma określonych powodów zmiany metryki, standardowo zalecane jest korzystanie z odległości statystycznej czyli metryki
Mahalanobisa– jest ona najbardziej uniwersalna, nie wymaga wcześniejszej standaryzacji danych i jest odporna na skorelowanie zmiennych. Dokładniejszy opis dostępnych w programie odległości i miar niepodobieństwa/podobieństwa oraz sposób ineterpretacji uzyskanych wyników można znaleźć w dziale Macierz podobieństwa.
W praktyce istnieje wiele metod wskazujących jak blisko znajdują się porównywane obiekty, w tym przypadku osoby leczone i nieleczone. W programie zaproponowane są dwie:
- Metoda najbliższego sąsiada – jest standardowym sposobem doboru obiektów nie tylko takich o podobnym Propensity Score, ale również takich których odległość/niepodobieństwo znajdujące się w macierzy jest najmniejsze.
- Metoda najbliższego sąsiada, bliższego niż… - działa w ten sam sposób, co metoda najbliższego sąsiada z tą różnicą, że dopasowane mogą zostać jedynie obiekty znajdujące się odpowiednio blisko. Granicę tej bliskości wyznaczamy podając wielkość opisującą próg, za którym znajdują się już obiekty tak niepodobne do badanych, że nie chcemy dać im szansy na dołączenie do nowo budowanej grupy kontrolnej. W przypadku gdy analiza opiera się na Propensity Score lub na macierzy określanej przez niepodobieństwo, najbardziej niepodobne obiekty to te odległe o 1, a najbardziej podobne, to te odległe o 0. Wybierając więc tę metodą należy podać wartość bliższą 0, gdy dobieramy bardziej restrykcyjnie, lub bliższą 1, gdy próg ten będzie umieszczony dalej. Gdy zamiast niepodobieństwa w macierzy wyznaczamy odległości, wówczas wielkość minimalna to wiąż 0, ale wielkość maksymalna nie jest z góry określona.
Dopasować możemy bez zwracania obiektów już wylosowanych lub ze zwracaniem tych obiektów ponownie do grupy, z której losujemy.
- Dopasowanie bez zwracania – w przypadku stosowania dopasowywania bez zwracania, gdy nieleczona osoba został wybrana do dopasowania do danej leczonej osoby, ta nieleczona osoba nie jest już dostępna do rozważenia jako potencjalne dopasowanie dla kolejnych osób leczonych. W rezultacie każda nieleczona osoba jest zawarta w co najwyżej jednym dopasowanym zestawie.
- Dopasowanie ze zwracaniem – dopasowanie ze zwracaniem pozwala na uwzględnienie danej nieleczonej osoby więcej niż raz w jednym dopasowanym zestawie. Kiedy stosuje się dopasowanie ze zwracaniem, dalsze analizy, a w szczególności oszacowanie wariancji musi uwzględniać fakt, że ta sama nieleczona osoba może znajdować się w wielu dopasowanych zestawach.
W przypadku gdy, nie da się jednoznacznie dobrać osoby nieleczonej do leczonej, ze względu na to, że w grupie z której wybieramy mamy więcej osób tak samo dobrze pasujących do osoby leczonej, wówczas połączona zostaje jedna z tych osób wybrana w sposób losowy. Dla wznowionej analizy domyślnie ustawiony jest stały seed, więc wyniki powtórzonego losowania będą te same, jednak gdy analizę wykonamy na nowo seed zostaje zmieniony i wynik losowania może być inny.
W przypadku gdy, nie da się dobrać osoby nieleczonej do leczonej, ze względu na to, że w grupie z której wybieramy nie ma już osób do dołączenia np. osoby pasujące zostały już dołączone do innych osób leczonych lub zbiór, z którego wybieramy nie ma osób podobnych, wówczas osoba ta pozostaje bez pary.
Najczęściej dokonuje się dopasowania 1:1, tzn. dla jednej osoby leczonej dobiera się jedną osobę nie leczoną. Jednak, jeśli oryginalna grupa kontrolna, z której dokonujemy losowania jest wystarczająco duża i potrzebujemy wylosować więcej osób, to można wybrać dopasowanie 1:k, gdzie k wskazuje liczbę osób, która powinna zostać dopasowana do każdej osoby leczonej.
Ocena dopasowania
Po dopasowaniu grupy kontrolnej do grupy leczonej wyniki takiego dopasowania możemy zwrócić do arkusza tzn. uzyskać nową grupę kontrolną. Nie należy jednak zakładać, że stosując dopasowanie zawsze uzyskamy satysfakcjonujące wyniki. W wielu sytuacjach grupa, z której losujemy nie posiada wystarczającej liczby takich obiektów, które są wystarczająco podobne do grupy leczonej. Dlatego zawsze wykonane dopasowanie należy ocenić. Istnieje wiele metod oceny dopasowania grup. W programie wykorzystano metody opierające się na standaryzowanej różnicy grup, szerzej opisywane m.in. w pracach P.C Austina 2)3). Takie podejście pozwala na porównanie względnej równowagi zmiennych mierzonych w różnych jednostkach, a na jego wynik nie ma wpływu wielkość próby. Zrezygnowano z oszacowania zgodności przy pomocy testów statystycznych, gdyż dobrana grupa kontrolna jest zwykle dużo mniejsza niż oryginalna grupa kontrolna, przez co uzyskiwane wartości p testów porównujących grupę badaną do mniejszej grupy kontrolnej częściej zostają z założeniem hipotezy zerowej, a więc nie wykazują istotnych różnic ze względu na zmniejszoną liczność.
Dla porównania zmiennych ciągłych wyznaczamy standaryzowaną różnicę średnich:

gdzie:
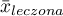 ,
, 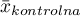 - to średnia wartość zmiennej w grupie leczonej i średnia wartość zmiennej w grupie kontrolnej,
- to średnia wartość zmiennej w grupie leczonej i średnia wartość zmiennej w grupie kontrolnej,
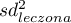 ,
, 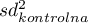 - to wariancja w grupie leczonej i wariancja w grupie kontrolnej.
- to wariancja w grupie leczonej i wariancja w grupie kontrolnej.
Dla porównania zmiennych binarnych (o dwóch kategoriach, zwykle 0 i 1) wyznaczamy standaryzowaną różnicę częstości:
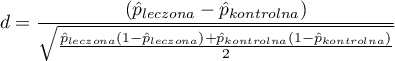
gdzie:
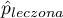 ,
, 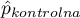 - to częstość wartości opisanej jako 1 w grupie leczonej i częstość wartości opisanej jako 1 w grupie kontrolnej.
- to częstość wartości opisanej jako 1 w grupie leczonej i częstość wartości opisanej jako 1 w grupie kontrolnej.
Zmienne o wielu kategoriach powinniśmy rozbić w analizie regresji logistycznej na zmienne fikcyjne o dwóch kategoriach i sprawdzając dopasowania obu grup wyznaczać dla nich standaryzowaną różnicę częstości.
Uwaga!
Chociaż nie ma powszechnie uzgodnionego kryterium określającego, jaki próg znormalizowanej różnicy można zastosować do wskazania istotnej nierównowagi, wskazówką może być standaryzowana różnica mniejsza niż 0.1 (zarówno w ocenie średnich jak i częstości)4). Dlatego, by uznać, że grupy są dobrze dobrane powinniśmy obserwować standaryzowane różnice położone blisko wartości 0, a najlepiej, by nie wychodziły poza przedział od -0.1 do 0.1. Graficznie wyniki te przedstawiamy na wykresie punktowym. Ujemne różnice świadczą o niższych średnich/częstościach w grupie leczonej, dodatnie w grupie kontrolnej.
Uwaga!
Uzyskane w raportach dopasowanie 1:1 oznacza podsumowanie dotyczące grupy badanej i odpowiadającej jej grupy kontrolnej uzyskanej w pierwszym dopasowaniu, dopasowanie 1:2 oznacza podsumowanie dotyczące grupy badanej i odpowiadającej jej grupy kontrolnej uzyskanej w pierwszym + drugim dopasowaniu (czyli nie dotyczy grupy badanej i odpowiadającej jej grupy kontrolnej uzyskanej tylko w drugim dopasowaniu), itd. –
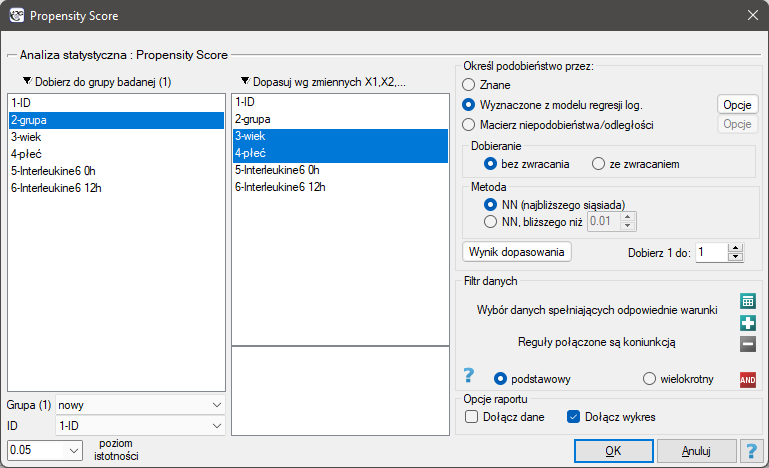
Okno z ustawieniami opcji dopasowania grup wywołujemy poprzez menu Statystyki zaawansowane→Modele wielowymiarowe→Dopasowanie grup
Przykład (plik dopasowanie.pqs)
Chcemy porównać dwa sposoby leczenia pacjentów po wypadkach, sposób tradycyjny i nowy sposób leczenia. Poprawne działanie obu sposobów leczenia powinno być obserwowane w obniżającym się poziomie wybranych cytokin. By porównać skuteczność tych dwóch sposobów leczenia obydwa one powinny zostać przeprowadzone na pacjentach, którzy są dość podobni. Wtedy będziemy mieli pewność, że ewentualne różnice w skuteczności tych metod będą wynikały z samego oddziaływania leczenia a nie z innych różnic między pacjentami przydzielonymi do różnych grup. Badanie jest przeprowadzone a posteriori, to znaczy bazuje na danych zebranych od pacjentów z historii leczenia. Dlatego badacze nie mieli wpływu na przypisanie pacjentów do grupy leczonej nowym lekiem i grupy leczonej tradycyjnie. Zauważono, że tradycyjny sposób leczenia był przepisywany głównie pacjentom starszym, podczas, gdy nowy sposób leczenia pacjentom w młodszym wieku, u których łatwiej jest obniżać poziom cytokin. Grupy były dość podobne co do struktury płci, ale nie identyczne.
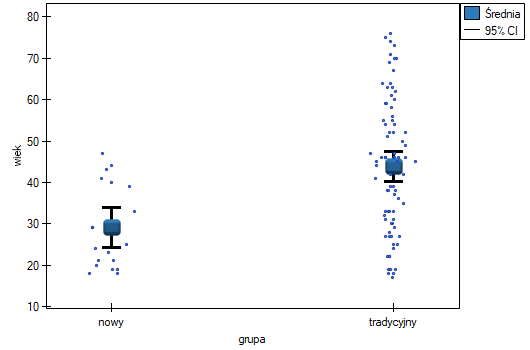
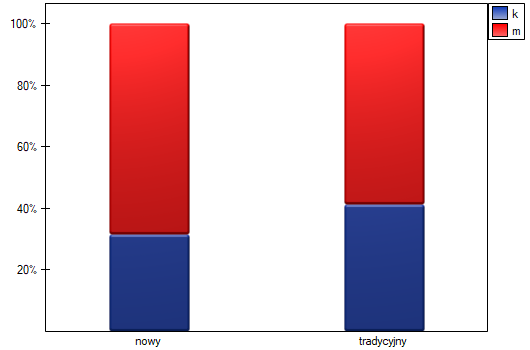
Gdyby przeprowadzono planowane badanie na tak wybranych grupach pacjentów, to nowy sposób miałby łatwiejsze zadanie do wykonania, gdyż młodsze organizmy lepiej mogłyby reagować na leczenie. Warunki eksperymentu nie byłyby równe dla obydwu sposobów, co mogłoby zafałszować wyniki analiz i wyciągane wnioski. Dlatego zdecydowano się dobrać grupę leczoną tradycyjnie tak, by była podobna do grupy badanej leczonej nowym sposobem. Dopasowania planujemy dokonać względem dwóch cech tzn. względem wieku i płci. Grupa leczona tradycyjnie jest większa (80 osób) od grupy leczonej nowym lekiem (19 osób), dlatego jest duża szansa na to, że uda się dobrać grupy tak, by były podobne. Losowego doboru dokonujemy poprzez algorytm modelu regresji logistycznej zaszyty w PSM. Pamiętamy, by płeć była zakodowana liczbowo, gdyż w analizie regresji logistycznej biorą udział jedynie wartości liczbowe. Jako metodę wybieramy najbliższe sąsiedztwo. Chcemy by ta sama osoba nie mogła zostać wybrana dwukrotnie, więc wybieramy losowanie bez zwracania. Spróbujemy dopasowania 1:1, czyli dla każdej osoby leczonej nowym lekiem dopasujemy jedną osobę leczoną tradycyjnie. Pamiętajmy przy tym, że dobór jest losowy, a więc zależy od losowej wartości seed ustawionej przez nasz komputer więc losowanie przeprowadzone przez czytelnika może się różnic od wartości przedstawionych tutaj.
Podsumowanie doboru obejrzymy w tabelach i na wykresach.
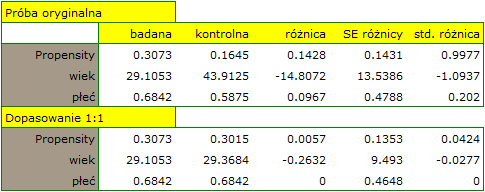
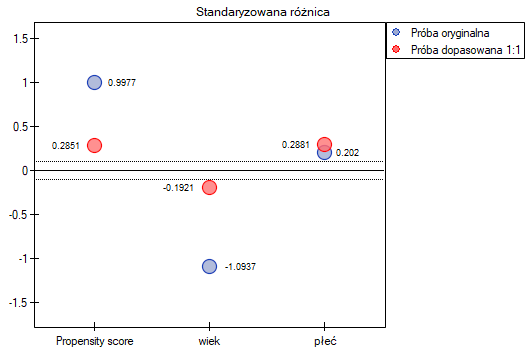
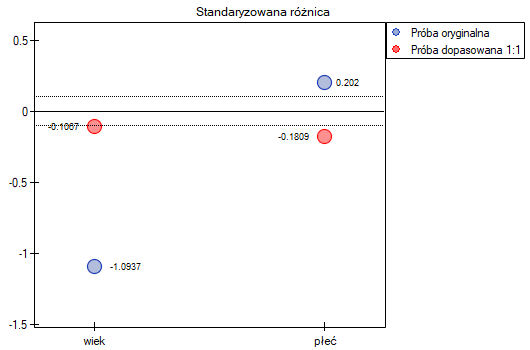
W próbie oryginalnej średnia wieku jest o ponad 14 lat wyższa u pacjentów leczonych tradycyjnie (różnica między średnimi wynosi 14.8072), natomiast struktura płci różni się o niecałe 10% (0.0967). Znacznie mniejsze różnice obserwujemy pomiędzy pacjentami leczonymi nowym sopsobem i dopasowanymi do nich osobami leczonymi tradycyjnie. Najwięcej informacji o jakości dopasowania uzyskamy na podstawie różnic standaryzowanych (ostatnia kolumna tabeli i wykres).
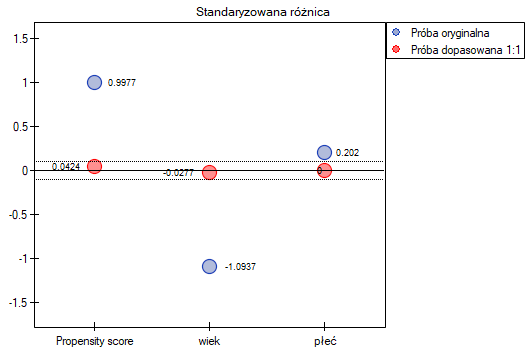
Linia na poziomie 0 oznacza równowagę grup (różnicę między grupami równą 0). Gdy grupy znajdują się w równowadze co do zadanych cech, wówczas wszystkie punkty na wykresie znajdują się blisko tej linii tzn. w okolicach przedziału od -0.1 do 0.1. W przypadku próby oryginalnej (kolor niebieski) widzimy znaczne oddalenie Propensity Score. Jak wiemy, ten brak dopasowania jest skutkiem głównie niedopasowania wieku – jego standaryzowana różnica znajduje się w dużej odległości od 0, a w mniejszym stopniu niedopasowania płci.
Dokonując dopasowania uzyskaliśmy grupy bardziej podobne do siebie (kolor czerwony na wykresie). Standaryzowana różnica między grupami określona przez Propensity Score wynosi 0.0424, czyli mieści sie w wyznaczonym przedziale. Wiek obu grup jest już podobny – grupa leczona tradycyjnie różni się od grupy leczonej nowym sposobem średnio o niecały rok (różnica między średnimi przedstawiona w tabeli to 0.2632) a standaryzowana różnica między średnimi wynosi -0.0277. W przypadku płci dopasowanie jest idealne, tzn. odsetek kobiet i mężczyzn jest taki sam w obu grupach (standaryzowana różnica odsetków przedstawiona w tabeli i na wykresie wynosi teraz 0). Tak przygotowane dane możemy zwrócić do arkusza i poddać planowanym przez siebie analizom.
Przyglądając się uzyskanemu przed chwilą podsumowaniu można zauważyć, że mimo dobrego zbalansowania grup i dobrania wielu osób idealnie, znajdują się pojedyncze osoby, które nie są do siebie tak podobne jak moglibyśmy oczekiwać.
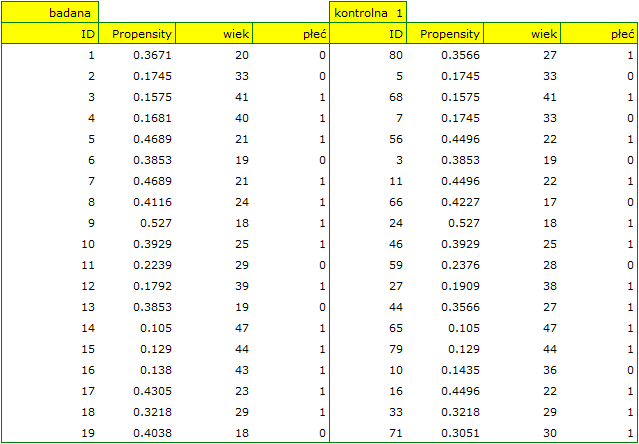
Czasami oprócz uzyskania grup dobrze zbalansowanych badaczom zależy na dokładnym określeniu sposobu doboru poszczególnych osób, tzn. uzyskaniu większego wpływu na podobieństwo obiektów co do wartości Propensity Score lub na podobieństwo obiektów co do wartości konkretnych cech. Wówczas, jeśli grupa z której losujemy jest wystarczająco liczna, analiza może przynieść korzystniejsze z punktu widzenia badacza efekty, ale gdy w grupie z której losujemy zabraknie obiektów spełniających nasze kryteria, wówczas dla części osób nie uda się znaleźć dopasowania spełniającego nasze warunki.
- Załóżmy, że chcielibyśmy uzyskać takie grupy, których Propensity Score (tzn. skłonność do wzięcia udziału w badaniu) różni się nie więcej niż …
Jak ustalić tę wartość? Można zerknąć na raport z wcześniejszej analizy, gdzie podana jest najmniejsza i największa odległość między losowanymi obiektami.

W naszym przypadku obiekty najbliższe sobie różnią się o min=0, a najdalsze o max=0.5183. Spróbujemy więc sprawdzić jaki dobór uzyskamy gdy będziemy dopasowywać do osób leczonych nową metodą takie osoby leczone tradycyjnie, których Propensity Score będzie bardzo bliskie np. mniejsze od 0.01.
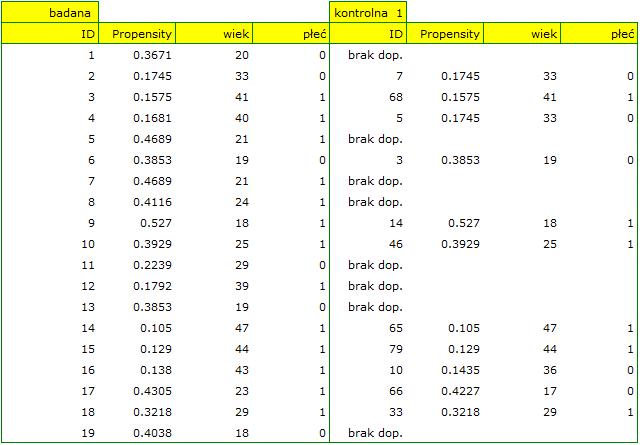
Widzimy, że tym razem z nie udało się dobrać całej grupy. Porównując Propensity Score dla poszczególnych par (leczonych nowym lekiem i leczonych tradycyjnie) widzimy, że różnice są naprawdę niewielkie. Jednak ze względu na to, że dobrana grupa jest znacznie mniejsza, to podsumowując cały proces doboru musimy zauważyć że zarówno Propensity Score, wiek jak i płeć nie znalazły się wystarczająco blisko linii na poziomie 0. Nasza chęć poprawy sytuacji nie doprowadziła do pożądanego skutku, a uzyskane grupy nie są wystarczająco dobrze zbalansowane.
- Załóżmy, że chcielibyśmy uzyskać takie pary (osób leczonych nową metodą i osób leczonych tradycyjnie), które są tej samej płci i których wiek nie różni się więcej niż 3 lata. W losowaniu opartym o Propensity Score nie mieliśmy tego typu możliwości wpływania na zakres zgodności każdej ze zmiennych. Do tego celu skorzystamy z innej metody, nie opartej na Propensity Score, ale bazującej na macierzach odległości/niepodobieństwa. Po wybraniu przycisku
Opcjewybieramy zaproponowaną macierz odległości statystycznej Mahalanobisa i ustawiamy dopasowanie sąsiedztwa na maksymalną odległość równą 3 dla wieku i równą 0 dla płci. W efekcie dla dwóch osób nie udało się znaleźć dopasowania, ale pozostałe dopasowania spełniają zadane kryteria.
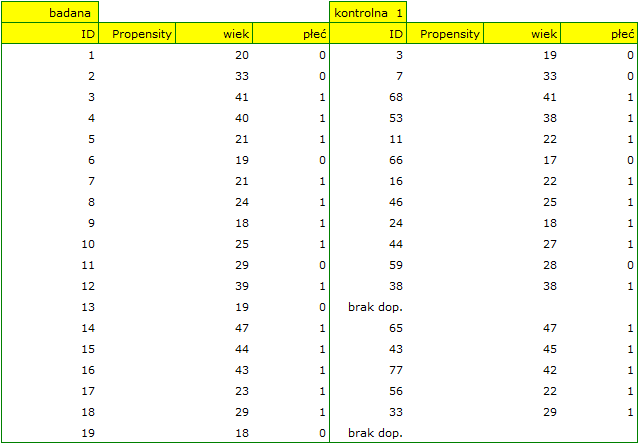
Podsumowując całościowo przeprowadzone losowanie musimy zauważyć, że mimo, że spełnia ono nasze założenia, to uzyskane grupy nie są tak dobrze zbalansowane jak to było w naszym pierwszym losowaniu przeprowadzonym w oparciu o Propensity Score. Punkty oznaczone kolorem czerwonym, przedstawiające jakość dopasowania pod względem wieku i jakość dopasowania pod względem płci odbiegają nieco od linii identyczności ustalonej na poziomie 0, co oznacza że średnia różnica wieku i struktury płci jest obecnie większa niż w pierwszym dopsowaniu.
To od badacza zależy, który sposób przygotowania danych będzie dla niego bardziej korzystny.
Ostatecznie, gdy decyzja zostanie podjęta, dane można zwrócić do nowego arkusza. By tego dokonać wracamy do wybranego przez siebie raportu i w drzewe projektu pod prawym przyciskiem wybieramy menu Powtórz analizę. W oknie tej samej analizy wskazujemy przycisk Wynik dopasowania i określamy, które jeszcze zmienne będą zwrócone do nowego arkusza.
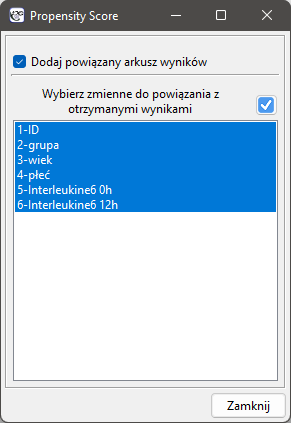
W efekcie otrzymamy nowy arkusz danych, w którym obok siebie znajdą się dane dotyczące osób leczonych nowym sposobem oraz dopasowanych do nich osób leczonych tradycyjnie.
2022/02/26 15:04
· admin
Interakcje
Interakcje rozważane są w modelach wielowymiarowych a ich występowanie oznacza, że wpływ zmiennej niezależnej ( ) na zmienną zależną (
) na zmienną zależną ( ) jest inny, w zależności od poziomu kolejnej zmiennej niezależnej (
) jest inny, w zależności od poziomu kolejnej zmiennej niezależnej ( ) lub szeregu kolejnych zmiennych niezależnych. By można było rozważać interekcje w modelach wielowymiarowych należy wskazać zmienne mówiące o prawdopodobnych interakcjach, czyli iloczyny odpowiednich zmiennych. W tym celu wybieramy przycisk
) lub szeregu kolejnych zmiennych niezależnych. By można było rozważać interekcje w modelach wielowymiarowych należy wskazać zmienne mówiące o prawdopodobnych interakcjach, czyli iloczyny odpowiednich zmiennych. W tym celu wybieramy przycisk Interakcje w oknie wybranej analizy wielowymiarowej. W oknie ustawiania interakcji z wciśniętym przyciskiem CTRL wskazujemy zmienne, które mają tworzyć interakcje i przenosimy je do sąsiedniej listy przy pomocy strzałki. Uruchamiając przycisk OK uzyskujemy odpowiednie kolumny w arkuszu danych.
W analizie interakcji wybór odpowiedniego kodowania zmiennych dychotomicznych pozwala na uniknięcie przeparametryzowania związanego z interakcjami. Przeparametryzowanie powoduje, że efekty niższego rzędu dla zmiennych dychotomicznych są redundantne względem uwikłanych interakcji wyższego rzędu. W rezultacie uwzględnienie w modelu interakcji wyższego rzędu niweluje efekt interakcji rzędów niższych, nie pozwalając na ich prawidłową ocenę. By uniknąć przeparametryzowania w modelu w którym występują interakcje zmiennych dychotomicznych zaleca się wybierać opcję kodowanie efektów.
W modelach z interakcjami należy pamiętać o odpowiednim ich „przycinaniu”, tak by usuwając efekty główne usunąć również efekty rzędów wyższych, które są od nich zależne. To znaczy: jeśli w modelu mamy następujące zmienne (efekty główne):  ,
,  ,
, 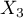 i interakcje:
i interakcje:  ,
,  ,
,  ,
, 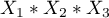 , to usuwając z modelu zmienną
, to usuwając z modelu zmienną  musimy usunąć również te interakcje, w których ona występuje, czyli:
musimy usunąć również te interakcje, w których ona występuje, czyli:  ,
,  oraz
oraz 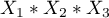 .
.
2014/08/22 20:00
Kodowanie zmiennych
Problemem w przygotowaniu danych do analizy wielowymiarowej jest odpowiednie zakodowanie zmiennych nominalnych i porządkowych. Jest to ważny element przygotowania danych do analizy, gdyż ma zasadniczy wpływ na interpretację współczynników modelu. Zmienne nominalne lub porządkowe dzielą analizowane obiekty na dwie lub więcej kategorii, przy czym zmienne dychotomiczne (o dwóch kategoriach, 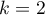 ) wystarczy tylko odpowiednio zakodować, a zmienne o wielu kategoriach (
) wystarczy tylko odpowiednio zakodować, a zmienne o wielu kategoriach (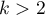 ) rozbić na zmienne fikcyjne (ang. dummy variable) o dwóch kategoriach oraz zakodować.
) rozbić na zmienne fikcyjne (ang. dummy variable) o dwóch kategoriach oraz zakodować.
- [
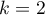 ] Jeśli zmienna jest dychotomiczna, badacz sam decyduje o sposobie, w jaki wprowadzi dane ją reprezentujące, może więc wprowadzić dowolne kody liczbowe np. 0 i 1. W programie można zmienić własne kodowanie na
] Jeśli zmienna jest dychotomiczna, badacz sam decyduje o sposobie, w jaki wprowadzi dane ją reprezentujące, może więc wprowadzić dowolne kody liczbowe np. 0 i 1. W programie można zmienić własne kodowanie na kodowanie efektuzaznaczając tę opcję w oknie wybranej analizy wielowymiarowej. Kodowanie takie powoduje zastąpienie mniejszej wartości wartością -1 a wartości większej wartością 1. - [
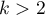 ] Jeśli zmienna ma wiele kategorii, to w oknie wybranej analizy wielowymiarowej wybieramy przycisk
] Jeśli zmienna ma wiele kategorii, to w oknie wybranej analizy wielowymiarowej wybieramy przycisk Zmienne fikcyjnei ustawiamy kategorię referencyjną/bazową dla tych zmiennych, które chcemy rozbić na zmienne fikcyjne. Zmienne te będą zakodowane zero-jedynkowo, chyba, że w oknie analizy zostanie wybrana opcjakodowanie efektu- wówczas kodowane będą jako -1, 0 i 1.
Kodowanie zero-jedynkowe (dummy coding) jest wykorzystywane by przy pomocy modeli wielowymiarowych odpowiedzieć na pytanie: Jak wyniki ( ), w każdej analizowanej kategorii, różnią się od wyników kategorii referencyjnej. Kodowanie to polega na przypisaniu wartości 0 lub 1 do każdej kategorii danej zmiennej. Kategoria zakodowana jako 0 jest wówczas kategorią referencyjną (reference).
), w każdej analizowanej kategorii, różnią się od wyników kategorii referencyjnej. Kodowanie to polega na przypisaniu wartości 0 lub 1 do każdej kategorii danej zmiennej. Kategoria zakodowana jako 0 jest wówczas kategorią referencyjną (reference).
- [
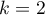 ] Gdy kodowana zmienna jest dychotomiczna, wówczas umieszczając ją w modelu regresji uzyskamy wyliczony dla niej współczynnik (
] Gdy kodowana zmienna jest dychotomiczna, wówczas umieszczając ją w modelu regresji uzyskamy wyliczony dla niej współczynnik (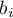 ). Współczynnik ten jest odniesieniem wartości zmiennej zależnej
). Współczynnik ten jest odniesieniem wartości zmiennej zależnej  dla kategorii 1 do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu).
dla kategorii 1 do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu). - [
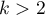 ] Gdy analizowana zmienna ma więcej niż dwie kategorie, wówczas
] Gdy analizowana zmienna ma więcej niż dwie kategorie, wówczas  kategorii jest reprezentowanych przez
kategorii jest reprezentowanych przez 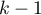 zmiennych fikcyjnych (dummy variables) o kodowaniu zero-jedynkowym. Tworząc zmienne o kodowaniu zero-jedynkowym wybiera się kategorię, dla której nie tworzy się zmiennej fikcyjnej. Kategoria ta traktowana jest w modelach jako kategoria odniesienia (gdyż w każdej zmiennej zakodowanej w sposób zero-jedynkowy odpowiadają jej wartości 0).
zmiennych fikcyjnych (dummy variables) o kodowaniu zero-jedynkowym. Tworząc zmienne o kodowaniu zero-jedynkowym wybiera się kategorię, dla której nie tworzy się zmiennej fikcyjnej. Kategoria ta traktowana jest w modelach jako kategoria odniesienia (gdyż w każdej zmiennej zakodowanej w sposób zero-jedynkowy odpowiadają jej wartości 0).
Gdy tak uzyskane zmienne 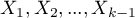 o kodowaniu zero-jedynkowym zostaną umieszczone w modelu regresji, wówczas zostaną dla nich wyliczone współczynniki
o kodowaniu zero-jedynkowym zostaną umieszczone w modelu regresji, wówczas zostaną dla nich wyliczone współczynniki  .
.
- [
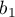 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w  ) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu);
) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu); - [
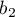 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w  ) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu)
) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu) - […]
- [
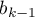 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w 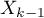 ) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu);
) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu);
Przykład
Zakodujemy zgodnie z kodowaniem zero-jedynkowym zmienną płeć o dwóch kategoriach (płeć męską wybierzemy jako kategorię referencyjną) i zmienną wykształcenie o 4 kategoriach (wykształcenie podstawowe wybierzemy jako referencyjne).
![LaTeX \begin{tabular}{|c|c|}
\hline
&\textcolor[rgb]{0.5,0,0.5}{\textbf{Zakodowna}}\\
\textbf{Płeć}&\textcolor[rgb]{0.5,0,0.5}{\textbf{płeć}}\\\hline
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/imgf1ab254dd632767d9aa15651e494953b.png)
![LaTeX \begin{tabular}{|c|ccc|}
\hline
& \multicolumn{3}{c|}{\textbf{Zakodowane wykształcenie}}\\
\textbf{Wykształcenie}&\textcolor[rgb]{0,0,1}{\textbf{zawodowe}}&\textcolor[rgb]{1,0,0}{\textbf{średnie}}&\textcolor[rgb]{0,0.58,0}{\textbf{wyższe}}\\\hline
\cellcolor[rgb]{0.88,0.88,0.88}podstawowe&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}podstawowe&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}podstawowe&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\textcolor[rgb]{0,0,1}{zawodowe}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{zawodowe}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{zawodowe}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{zawodowe}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{1,0,0}{średnie}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{średnie}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{średnie}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{średnie}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
...&...&...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img888a1cc4d1abe65cc7c2628e3f564b45.png)
Budując na podstawie zmiennych fikcyjnych, w modelu regresji wielorakiej, moglibyśmy chcieć sprawdzić jak zmienne te wpływają na pewną zmienną zależną np.  = wysokość zarobków (wyrażoną w tysiącach złotych). W wyniku takiej analizy dla każdej zmiennej fikcyjnej uzyskamy przykładowe współczynniki:
= wysokość zarobków (wyrażoną w tysiącach złotych). W wyniku takiej analizy dla każdej zmiennej fikcyjnej uzyskamy przykładowe współczynniki:
- dla płci istotny statystycznie współczynnik 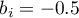 - co oznacza, że średnie zarobki kobiet są o pół tysiąca złoty niższe niż mężczyzn; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki kobiet są o pół tysiąca złoty niższe niż mężczyzn; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla wykształcenia zawodowego istotny statystycznie współczynnik 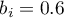 - co oznacza, że średnie zarobki osób z wykształceniem zawodowym są o 0.6 tysiąca złoty wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki osób z wykształceniem zawodowym są o 0.6 tysiąca złoty wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla wykształcenia średniego istotny statystycznie współczynnik 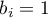 - oznacza, że średnie zarobki osób z wykształceniem średnim są o tysiąc złoty wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- oznacza, że średnie zarobki osób z wykształceniem średnim są o tysiąc złoty wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla wykształcenia wyższego istotny statystycznie współczynnik 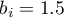 - co oznacza, że średnie zarobki osób z wykształceniem wyższym są o 1.5 tysiąca wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie.
- co oznacza, że średnie zarobki osób z wykształceniem wyższym są o 1.5 tysiąca wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie.
Kodowanie efektów (effect coding) jest wykorzystywane, by przy pomocy modeli wielowymiarowych odpowiedzieć na pytanie: Jak wyniki ( ), w każdej analizowanej kategorii, różnią się od wyników średniej (nieważonej) uzyskanej z próby. Kodowanie to polega na przypisaniu wartości -1 lub 1 do każdej kategorii danej zmiennej. Kategoria zakodowana jako -1 jest wówczas kategorią bazową (base)
), w każdej analizowanej kategorii, różnią się od wyników średniej (nieważonej) uzyskanej z próby. Kodowanie to polega na przypisaniu wartości -1 lub 1 do każdej kategorii danej zmiennej. Kategoria zakodowana jako -1 jest wówczas kategorią bazową (base)
- [
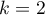 ] Gdy kodowana zmienna jest dychotomiczna, wówczas umieszczając ją w modelu regresji uzyskamy wyliczony dla niej współczynnik (
] Gdy kodowana zmienna jest dychotomiczna, wówczas umieszczając ją w modelu regresji uzyskamy wyliczony dla niej współczynnik (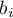 ). Współczynnik ten jest odniesieniem
). Współczynnik ten jest odniesieniem  dla kategorii 1 do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu).
dla kategorii 1 do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu).
Gdy analizowana zmienna ma więcej niż dwie kategorie, wówczas  kategorii jest reprezentowanych przez
kategorii jest reprezentowanych przez 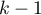 zmiennych fikcyjnych o kodowaniu efektu. Tworząc zmienne o kodowaniu efektu wybiera się kategorię dla której nie tworzy się oddzielnej zmiennej. Kategoria ta traktowana jest w modelach jako kategoria bazowa (gdyż w każdej zmiennej zapisanej poprzez kodowanie efektu odpowiadają jej wartości -1).
zmiennych fikcyjnych o kodowaniu efektu. Tworząc zmienne o kodowaniu efektu wybiera się kategorię dla której nie tworzy się oddzielnej zmiennej. Kategoria ta traktowana jest w modelach jako kategoria bazowa (gdyż w każdej zmiennej zapisanej poprzez kodowanie efektu odpowiadają jej wartości -1).
Gdy tak uzyskane zmienne 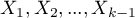 o kodowaniu efektu zostaną umieszczone w modelu regresji, wówczas zostaną dla nich wyliczone współczynniki
o kodowaniu efektu zostaną umieszczone w modelu regresji, wówczas zostaną dla nich wyliczone współczynniki  .
.
- [
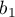 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w  ) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu);
) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu); - [
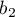 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w  ) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu);
) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu); - […]
- [
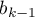 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w 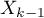 ) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu);
) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu);
Przykład
Zakodujemy przy pomocy kodowania efektu zmienną płeć o dwóch kategoriach (płeć męską wybierzemy jako kategorię bazową) i zmienną wskazującą region zamieszkania na terenie analizowanego kraju. Wyróżniono 5 regionów: północny, południowy, wschodni, zachodni i centralny - region centralny wybierzemy jako bazowy.
![LaTeX \begin{tabular}{|c|c|}
\hline
&\textcolor[rgb]{0.5,0,0.5}{\textbf{Zakodowona}}\\
\textbf{Płeć}&\textcolor[rgb]{0.5,0,0.5}{\textbf{płeć}}\\\hline
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img8517130d5e2791d315ceb261541be124.png)
![LaTeX \begin{tabular}{|c|cccc|}
\hline
\textbf{Region}& \multicolumn{4}{c|}{\textbf{Zakodowany region}}\\
\textbf{zamieszkania}&\textcolor[rgb]{0,0,1}{\textbf{zachodni}}&\textcolor[rgb]{1,0,0}{\textbf{wschodni}}&\textcolor[rgb]{0,0.58,0}{\textbf{północny}}&\textcolor[rgb]{0.55,0,0}{\textbf{południowy}}\\\hline
\cellcolor[rgb]{0.88,0.88,0.88}centralny&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}centralny&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}centralny&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\textcolor[rgb]{0,0,1}{zachodni}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{zachodni}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{zachodni}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{zachodni}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{1,0,0}{wschodni}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{wschodni}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{wschodni}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{wschodni}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{0,0.58,0}{północny}&0&0&\textcolor[rgb]{0,0.58,0}{1}&0\\
\textcolor[rgb]{0,0.58,0}{północny}&0&0&\textcolor[rgb]{0,0.58,0}{1}&0\\
\textcolor[rgb]{0.55,0,0}{południowy}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
\textcolor[rgb]{0.55,0,0}{południowy}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
\textcolor[rgb]{0.55,0,0}{południowy}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
...&...&...&...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/imgdc3ad26cbc6bbae2fa20fd348bd79e41.png)
Budując na podstawie zmiennych fikcyjnych, w modelu regresji wielorakiej, moglibyśmy chcieć sprawdzić jak zmienne te wpływają na pewną zmienną zależną np.  = wysokość zarobków (wyrażoną w tysiącach złotych). W wyniku takiej analizy dla każdej zmiennej fikcyjnej uzyskamy przykładowe współczynnik:
= wysokość zarobków (wyrażoną w tysiącach złotych). W wyniku takiej analizy dla każdej zmiennej fikcyjnej uzyskamy przykładowe współczynnik:
- dla płci istotny statystycznie współczynnik 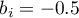 - co oznacza, że średnie zarobki kobiet są o pół tysiąca złoty niższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki kobiet są o pół tysiąca złoty niższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla regionu zachodniego istotny statystycznie współczynnik 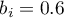 - co oznacza, że średnie zarobki osób zamieszkujących na zachodzie kraju są o 0.6 tysiąca złoty wyższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki osób zamieszkujących na zachodzie kraju są o 0.6 tysiąca złoty wyższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla regionu wschodniego istotny statystycznie współczynnik  - oznacza, że średnie zarobki osób zamieszkujących na wschodzie kraju są o tysiąc złoty niższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- oznacza, że średnie zarobki osób zamieszkujących na wschodzie kraju są o tysiąc złoty niższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla regionu północnego istotny statystycznie współczynnik 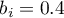 - co oznacza, że średnie zarobki osób zamieszkujących na północy są o 0.4 tysiąca wyższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki osób zamieszkujących na północy są o 0.4 tysiąca wyższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla regionu południowego nieistotny statystycznie współczynnik 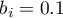 - co oznacza, że średnie zarobki osób zamieszkujących na południu nie różnią się istotnie od średnich zarobków w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie.
- co oznacza, że średnie zarobki osób zamieszkujących na południu nie różnią się istotnie od średnich zarobków w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie.
2014/08/22 20:00
2014/08/22 20:00
Liniowa regresja wieloraka
Okno z ustawieniami opcji Regresji wielorakiej wywołujemy poprzez menu Statystyka zaawansowana→Modele wielowymiarowe→Regresja wieloraka
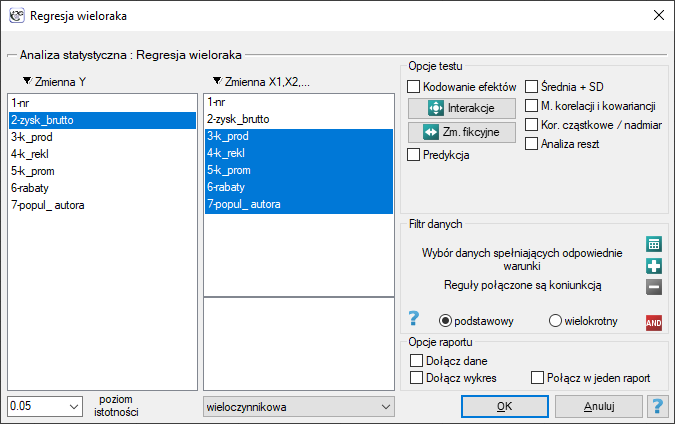
 Budowany model regresji wielorakiej pozwala na zbadanie wpływu wielu zmiennych niezależnych (
Budowany model regresji wielorakiej pozwala na zbadanie wpływu wielu zmiennych niezależnych ( ,
,  ,
,  ,
, 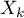 ) na jedną zmienną zależną (
) na jedną zmienną zależną ( ). Najczęściej wykorzystywaną odmianą regresji wielorakiej jest Liniowa Regresja Wieloraka. Jest ona rozszerzeniem modeli regresji liniowej opartej o współczynnik korelacji liniowej Pearsona. Zakłada ona występowanie liniowego związku pomiędzy badanymi zmiennymi. Liniowy model regresji wielorakiej przyjmuje postać:
). Najczęściej wykorzystywaną odmianą regresji wielorakiej jest Liniowa Regresja Wieloraka. Jest ona rozszerzeniem modeli regresji liniowej opartej o współczynnik korelacji liniowej Pearsona. Zakłada ona występowanie liniowego związku pomiędzy badanymi zmiennymi. Liniowy model regresji wielorakiej przyjmuje postać:
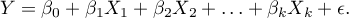
gdzie:
 - zmienna zależna, objaśniana przez model,
- zmienna zależna, objaśniana przez model,
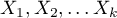 - zmienne niezależne, objaśniające,
- zmienne niezależne, objaśniające,
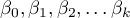 - parametry,
- parametry,
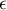 - składnik losowy (reszta modelu).
- składnik losowy (reszta modelu).
Jeśli model został stworzony w oparciu o próbę o liczności  powyższe równanie można przedstawić w postaci macierzowej:
powyższe równanie można przedstawić w postaci macierzowej:
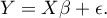
gdzie:
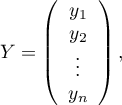

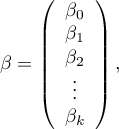
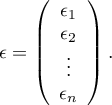
Rozwiązaniem równania jest wówczas wektor ocen parametrów 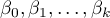 nazywanych współczynnikami regresji:
nazywanych współczynnikami regresji:
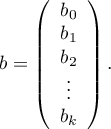
Współczynniki te szacowane są poprzez klasyczną metodę najmniejszych kwadratów. Na podstawie tych wartości możemy wnioskować o wielkości wpływu zmiennej niezależnej (dla której ten współczynnik został oszacowany) na zmienną zależną. Podają o ile jednostek zmieni się zmienna zależna, gdy zmienną niezależną zmienimy o 1 jednostkę. Każdy współczynnik obarczony jest pewnym błędem szacunku. Wielkość tego błędu wyliczana jest ze wzoru:
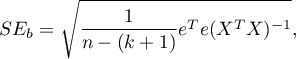
gdzie:
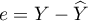 to wektor reszt modelu (różnica pomiędzy rzeczywistymi wartościami zmiennej zależnej Y a wartościami
to wektor reszt modelu (różnica pomiędzy rzeczywistymi wartościami zmiennej zależnej Y a wartościami 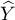 przewidywanymi na podstawie modelu).
przewidywanymi na podstawie modelu).
Zmienne fikcyjne i interakcje w modelu
Omówienie przygotowania zmiennych fikcyjnych i interakcji przedstawiono w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
Uwaga!
Budując model należy pamiętać, że liczba obserwacji musi być duża, to znaczy powinna spełniać założenie: 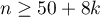 , gdzie k, to liczba zmiennych objaśniających w modelu 5).
, gdzie k, to liczba zmiennych objaśniających w modelu 5).
Weryfikacja modelu
- Istotność statystyczna poszczególnych zmiennych w modelu.
Na podstawie współczynnika oraz jego błędu szacunku możemy wnioskować czy zmienna niezależna, dla której ten współczynnik został oszacowany wywiera istotny wpływ na zmienną zależną. W tym celu posługujemy się testem t-Studenta.
Hipotezy:
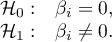
Wyliczmy statystykę testową według wzoru:
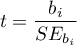
Statystyka testowa ma rozkład t-Studenta z 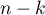 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Jakość zbudowanego modelu liniowej regresji wielorakiej możemy ocenić kilkoma miarami.
- Błąd standardowy estymacji - jest miarą dopasowania modelu:
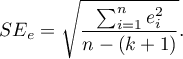
Miara ta opiera się na resztach modelu 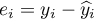 , czyli rozbieżności pomiędzy rzeczywistymi wartościami zmiennej zależnej
, czyli rozbieżności pomiędzy rzeczywistymi wartościami zmiennej zależnej 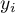 w próbie a wartościami zmiennej zależnej
w próbie a wartościami zmiennej zależnej 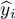 wyliczonej na podstawie zbudowanego modelu. Najlepiej byłoby, gdyby różnica ta była jak najbliższa zeru dla wszystkich badanych obiektów próby. Zatem, aby model był dobrze dopasowany, błąd standardowy estymacji (
wyliczonej na podstawie zbudowanego modelu. Najlepiej byłoby, gdyby różnica ta była jak najbliższa zeru dla wszystkich badanych obiektów próby. Zatem, aby model był dobrze dopasowany, błąd standardowy estymacji (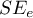 ) wyrażony jako wariancja
) wyrażony jako wariancja 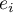 , powinien być jak najmniejszy.
, powinien być jak najmniejszy.
- Współczynnik korelacji wielorakiej
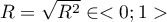 - określa siłę oddziaływania zespołu zmiennych
- określa siłę oddziaływania zespołu zmiennych 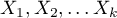 na zmienną zależną
na zmienną zależną  .
.
- Współczynnik determinacji wielorakiej
 - jest miarą dopasowania modelu.
- jest miarą dopasowania modelu.
Wartość tego współczynnika mieści się w przedziale 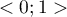 , gdzie 1 oznacza doskonałe dopasowanie modelu, 0 - zupełny bark dopasowania. W jego wyznaczeniu posługujemy się następującą równością:
, gdzie 1 oznacza doskonałe dopasowanie modelu, 0 - zupełny bark dopasowania. W jego wyznaczeniu posługujemy się następującą równością:
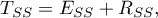
gdzie:
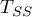 - całkowita suma kwadratów,
- całkowita suma kwadratów,
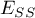 - suma kwadratów wyjaśniona przez model,
- suma kwadratów wyjaśniona przez model,
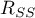 - resztowa suma kwadratów.
- resztowa suma kwadratów.
Współczynnik determinacji wyliczamy z wzoru:
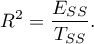
Wyraża on procent zmienności zmiennej zależnej tłumaczony przez model.
Ponieważ wartość współczynnika  zależy od dopasowania modelu, ale jest również wrażliwa na ilość zmiennych w modelu i liczność próby, bywają sytuacje, w których może być obarczona pewnym błędem. Dalego też wyznacza się poprawianą wartość tego parametru:
zależy od dopasowania modelu, ale jest również wrażliwa na ilość zmiennych w modelu i liczność próby, bywają sytuacje, w których może być obarczona pewnym błędem. Dalego też wyznacza się poprawianą wartość tego parametru:
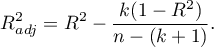
- Kryteria informacyjne opierają się na entropii informacji niesionej przez model (niepewności modelu) tzn. szacują utraconą informację, gdy dany model jest używany do opisu badanego zjawiska. Powinniśmy zatem wybierać model o minimalnej wartości danego kryterium informacyjnego.
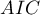 ,
, 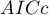 i
i 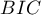 jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu (
jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu ( ) i liczności próby (
) i liczności próby ( ). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
Kryterium informacyjne Akaikego (ang. Akaike information criterion)
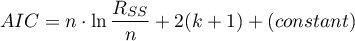
gdzie, stałą można pominąć, ponieważ jest taka sama w każdym z porównywanych modeli.
Jest to kryterium asymptotyczne - odpowiednie dla dużych prób tzn. gdy 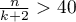 . Przy małych próbach ma tendencję do preferowania modeli z dużą liczbą zmiennych.
. Przy małych próbach ma tendencję do preferowania modeli z dużą liczbą zmiennych.
Przykład interpretacji porównania wielkości AIC
Załóżmy, że wyznaczyliśmy AIC dla trzech modeli AIC1=100, AIC2=101.4, AIC3=110. Wówczas można wyznaczyć względną wiarygodność dla modelu. Wiarygodność ta jest względna, gdyż wyznaczana jest względem innego modelu, najczęściej tego o najmniejszej wartości AIC. Wyznaczamy ją wg wzoru: exp((AICmin− AICi)/2). Porównując model 2 do modelu pierwszego powiemy, że prawdopodobieństwo, iż zminimalizuje on utratę informacji stanowi około połowę prawdopodobieństwa, że zrobi to model 1 (a dokładnie exp((100− 101.4)/2) = 0.497). Porównując model 3 do modelu pierwszego powiemy, że prawdopodobieństwo, iż zminimalizuje on utratę informacji stanowi niewielką część prawdopodobieństwa, że zrobi to model 1 (a dokładnie exp((100- 110)/2) = 0.007).
Poprawione kryterium informacyjne Akaikego
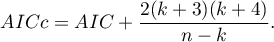
Poprawka kryterium Akaikego dotyczy wielkości próby, przez co jest to miara rekomendowana również dla prób o małych licznościach.
Bayesowskie kryterium informacyjne Schwartza (ang. Bayes Information Criterion lub Schwarz criterion)
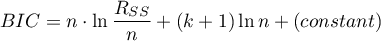
gdzie, stałą można pominąć, ponieważ jest taka sama w każdym z porównywanych modeli.
Podobnie jak poprawione kryterium Akaikego BIC uwzględnia wielkość próby.
- Analiza błędów dla prognoz ex post:
MAE (średni błąd bezwzględny) ang. mean absolute error – trafność prognozy określona przez MAE informuje o ile średnio uzyskiwane realizacje zmiennej zależnej będę się odchylać (co do wartości bezwzględnej) od prognoz.
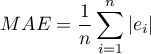
MPE (średni błąd procentowy) ang. mean percentage error – informuje, jaki średni procent realizacji zmiennej zależnej stanowią błędy prognozy.
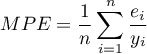
MAPE (średni bezwzględny błąd procentowy) ang. mean absolute percentage error – informuje o średniej wielkości błędów prognoz wyrażonych w procentach rzeczywistych wartości zmiennej zależnej. MAPE pozwala porównać dokładność prognoz uzyskanych na bazie różnych modeli.
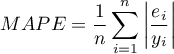
- Istotność statystyczna wszystkich zmiennych w modelu
Podstawowym narzędziem szacującym istotność wszystkich zmiennych w modelu jest test analizy wariancji (test F). Test ten weryfikuje jednocześnie 3 równoważne hipotezy:


Statystyka testowa ma postać:
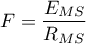
gdzie:
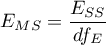 - średnia kwadratów wyjaśniona przez model,
- średnia kwadratów wyjaśniona przez model,
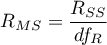 - resztowa średnia kwadratów,
- resztowa średnia kwadratów,
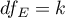 ,
, 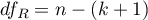 - odpowiednie stopnie swobody.
- odpowiednie stopnie swobody.
Statystyka ta podlega rozkładowi F Snedecora z 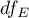 i
i 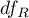 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przykład c.d. (plik wydawca.pqs)
2014/08/22 20:00
Więcej informacji o zmiennych w modelu
- Standaryzowane
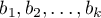 - w odróżnieniu od parametrów surowych (które w zależności od opisywanej zmiennej są wyrażone w różnych jednostkach miary i nie mogą być bezpośrednio porównywane) standaryzowane oceny parametrów modelu pozwalają porównywać wkład poszczególnych zmiennych w wyjaśnienie zmienności zmiennej zależnej
- w odróżnieniu od parametrów surowych (które w zależności od opisywanej zmiennej są wyrażone w różnych jednostkach miary i nie mogą być bezpośrednio porównywane) standaryzowane oceny parametrów modelu pozwalają porównywać wkład poszczególnych zmiennych w wyjaśnienie zmienności zmiennej zależnej  .
.
- Macierz korelacji - zawiera informacje o sile związku pomiędzy poszczególnymi zmiennymi, czyli współczynnik korelacji Pearsona
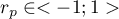 . Współczynnikiem tym badamy korelację dla każdej pary zmiennych, nie uwzględniając wpływu pozostałych zmiennych w modelu.
. Współczynnikiem tym badamy korelację dla każdej pary zmiennych, nie uwzględniając wpływu pozostałych zmiennych w modelu.
- Macierz kowariancji - podobnie jak macierz korelacji, zawiera informacje o związku liniowym pomiędzy poszczególnymi zmiennymi. Przy czym wartość ta nie jest wystandaryzowana.
- Współczynnik korelacji cząstkowej - należy do przedziału
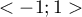 i jest miarą korelacji pomiędzy konkretną zmienną niezależną
i jest miarą korelacji pomiędzy konkretną zmienną niezależną 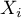 (uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu) a zmienną zależną
(uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu) a zmienną zależną  (uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu).
(uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu).
Kwadrat tego współczynnika to współczynnik determinacji cząstkowej - należy do przedziału 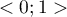 i oznacza stosunek wyłącznej zmienności danej zmiennej niezależnej
i oznacza stosunek wyłącznej zmienności danej zmiennej niezależnej 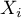 do tej zmienności zmiennej zależnej
do tej zmienności zmiennej zależnej  , która nie została wyjaśniona przez pozostałe zmienne w modelu.
, która nie została wyjaśniona przez pozostałe zmienne w modelu.
Im wartość tych współczynników znajduje się bliżej 0, tym bardziej bezużyteczną informację niesie badana zmienna, czyli jest ona nadmiarowa.
- Współczynnik korelacji semicząstkowej - należy do przedziału
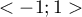 i jest miarą korelacji pomiędzy konkretną zmienną niezależną
i jest miarą korelacji pomiędzy konkretną zmienną niezależną 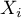 (uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu) a zmienną zależną
(uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu) a zmienną zależną  (NIE uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu).
(NIE uwzględniając jej skorelowanie z pozostałymi zmiennymi w modelu).
Kwadrat tego współczynnika to współczynnik determinacji semicząstkowej - należy do przedziału 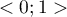 i oznacza stosunek wyłącznej zmienności danej zmiennej niezależnej
i oznacza stosunek wyłącznej zmienności danej zmiennej niezależnej 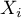 do całkowitej zmienności zmiennej zależnej
do całkowitej zmienności zmiennej zależnej  .
.
Im wartość tych współczynników znajduje się bliżej zera, tym bardziej bezużyteczną informację niesie badana zmienna, czyli jest ona nadmiarowa.
- R-kwadrat (
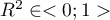 ) - wyraża on procent zmienności danej zmiennej niezależnej
) - wyraża on procent zmienności danej zmiennej niezależnej 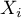 tłumaczony przez pozostałe zmienne niezależne. Im bliżej wartości 1 tym silniej badana zmienna związana jest liniowo z pozostałymi zmiennymi niezależnymi, co może oznaczać, że jest ona zmienną nadmiarową.
tłumaczony przez pozostałe zmienne niezależne. Im bliżej wartości 1 tym silniej badana zmienna związana jest liniowo z pozostałymi zmiennymi niezależnymi, co może oznaczać, że jest ona zmienną nadmiarową.
- współczynnik inflacji wariancji (
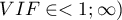 ) - określa jak bardzo wariancja szacowanego współczynnika regresji jest zwiększona z powodu współliniowości. Im bliżej wartości 1, tym mniejsza współliniowość i tym mniejszy jej wpływ na wariancję współczynnika. Przyjmuje się, że silna współliniowość występuje, gdy współczynnik VIF>5 6). Jeśli współczynnik inflacji wariancji wynosi 5 (
) - określa jak bardzo wariancja szacowanego współczynnika regresji jest zwiększona z powodu współliniowości. Im bliżej wartości 1, tym mniejsza współliniowość i tym mniejszy jej wpływ na wariancję współczynnika. Przyjmuje się, że silna współliniowość występuje, gdy współczynnik VIF>5 6). Jeśli współczynnik inflacji wariancji wynosi 5 (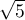 = 2.2), oznacza to, że błąd standardowy dla współczynnika tej zmiennej jest 2.2 razy większy niż w przypadku, gdyby ta zmienna miała zerową korelację z innymi zmiennymi
= 2.2), oznacza to, że błąd standardowy dla współczynnika tej zmiennej jest 2.2 razy większy niż w przypadku, gdyby ta zmienna miała zerową korelację z innymi zmiennymi 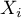 .
.
- Tolerancja =
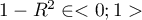 - wyraża on procent zmienności danej zmiennej niezależnej
- wyraża on procent zmienności danej zmiennej niezależnej 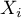 NIE tłumaczony przez pozostałe zmienne niezależne. Im wartość tolerancji jest bliższa 0 tym silniej badana zmienna związana jest liniowo z pozostałymi zmiennymi niezależnymi, co może oznaczać, że jest ona zmienną nadmiarową.
NIE tłumaczony przez pozostałe zmienne niezależne. Im wartość tolerancji jest bliższa 0 tym silniej badana zmienna związana jest liniowo z pozostałymi zmiennymi niezależnymi, co może oznaczać, że jest ona zmienną nadmiarową.
- Porównanie modelu pełnego z modelem po usunięciu danej zmiennej
Porównanie tych dwóch modeli dokonujemy:
- testem F, w sytuacji gdy z modelu usuwamy jedną zmienną lub wiecej niż jedną zmienną (patrz porównywanie modeli),
- testem t-Studenta, gdy z modelu usuwamy tylko jedną zmienną. Jest to ten sam test, którym badamy istotność poszczególnych zmiennych w modelu.
W przypadku usunięcia tylko jednej zmiennej wyniki obu tych testów są tożsame.
Jeśli różnica pomiędzy porównywanymi modelami jest istotna statystycznie (wartość 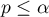 ), wówczas model pełny jest istotnie lepszy niż model zredukowany. To oznacza, że badana zmienna nie jest nadmiarowa, wywiera ona istotny wpływ na dany model i nie powinna być z niego usuwana.
), wówczas model pełny jest istotnie lepszy niż model zredukowany. To oznacza, że badana zmienna nie jest nadmiarowa, wywiera ona istotny wpływ na dany model i nie powinna być z niego usuwana.
- Wykresy rozrzutu
Wykresy te pozwalają dokonać subiektywnej oceny liniowości związku pomiędzy zmiennymi i zidentyfikować punkty odstające. Dodatkowo wykresami rozrzutu możemy posłużyć się w analizie reszt modelu.
2014/08/22 20:00
Analiza reszt modelu
By otrzymać poprawny model regresji, powinniśmy sprawdzić podstawowe założenia dotyczące reszt modelu.
- Obserwacje odstające
Badając reszty modelu szybko można uzyskać wiedzę na temat wartości odstających. Obserwacje takie mogą bardzo zaburzyć równanie regresji, ponieważ mają duży wpływ na wartości współczynników tego równania. Jeśli dana reszta 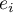 jest oddalona o więcej niż 3 odchylenia standardowe od wartości średniej, wówczas obserwacje taką można uznać za obserwacje odstającą. Usunięcie obserwacji odstającej może w znaczącym stopniu przyczynić się do poprawy modelu.
jest oddalona o więcej niż 3 odchylenia standardowe od wartości średniej, wówczas obserwacje taką można uznać za obserwacje odstającą. Usunięcie obserwacji odstającej może w znaczącym stopniu przyczynić się do poprawy modelu.
Odległość Cooka - opisuje wielkość zmian współczynników regresji powstałą na skutek pominięcia danego przypadku. W programie zaznaczone pogrubioną czcionką są odległości Cooka dla przypadków, które przekraczają 50 percentyl statystyki rozkładu Fishera-Snedecora F(0.5, k+1, n−k−1).
Odległość Mahalanobisa - dedykowana jest do wykrywania obserwacji odstających - wysokie wartości świadczą o znacznym oddaleniu danego przypadku od centrum zmiennych niezależnych. Jeśli wśród przypadków oddalonych o więcej niż 3 odchylenia znajdzie się przypadek o największej wartości Mahalanobisa, wówczas jako najbardziej odstający zostanie on zaznaczony pogrubioną czcionką.
- Normalność rozkładu reszt modelu
Założenie to sprawdzamy wizualnie przy pomocy wykresu Q-Q rozkładu nromalnego. Duża różnica między rozkładem reszt a rozkładem normalnym może zaburzać ocenę istotności współczynników poszczególnych zmiennych modelu..
- Homoskedastyczność (stałość wariancji)
By sprawdzić czy istnieją obszary, gdzie wariancja reszt modelu jest zwiększona lub zmniejszona posługujemy się wykresami:
- reszty względem wartości przewidywanych
- kwadrat reszty względem wartości przewidywanych
- reszty względem wartości obserwowanych
- kwadrat reszty względem wartości obserwowanych
- Autokorelacja reszt modelu
Aby zbudowany model można było uznać za poprawny, wartości reszt nie powinny być ze sobą skorelowane (dla wszystkich par 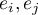 ). Założenie to możemy sprawdzić wyliczając statystykę testu Durbina-Watsona
). Założenie to możemy sprawdzić wyliczając statystykę testu Durbina-Watsona
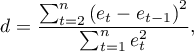
Aby sprawdzić dodatnią autokorelację na poziomie istotności  , sprawdzamy położenie statystyki
, sprawdzamy położenie statystyki 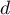 w stosunku do górnej (
w stosunku do górnej (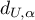 ) i dolnej (
) i dolnej (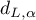 ) wartości krytycznej:
) wartości krytycznej:
- Jeżeli
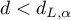 - błędy są dodatnio skorelowane;
- błędy są dodatnio skorelowane; - Jeśli
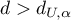 - błędy nie są dodatnio skorelowane;
- błędy nie są dodatnio skorelowane; - Jeśli
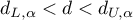 - wynik testu jest niejednoznaczny.
- wynik testu jest niejednoznaczny.
Aby sprawdzić ujemną autokorelację na poziomie istotności  , sprawdzamy położenie wartości
, sprawdzamy położenie wartości 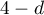 w stosunku do górnej (
w stosunku do górnej (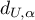 ) i dolnej (
) i dolnej (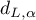 ) wartości krytycznej:
) wartości krytycznej:
- Jeżeli
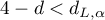 - błędy są ujemnie skorelowane;
- błędy są ujemnie skorelowane; - Jeśli
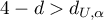 - błędy nie są ujemnie skorelowane;
- błędy nie są ujemnie skorelowane; - Jeśli
 - wynik testu jest niejednoznaczny.
- wynik testu jest niejednoznaczny.
Wartości krytyczne testu Durbina-Watsona dla poziomu istotności  znajdują się na stronie internetowej (pqstat) - źródło tablic: Savina i White (1977)7)
znajdują się na stronie internetowej (pqstat) - źródło tablic: Savina i White (1977)7)
Przykład c.d. (plik wydawca.pqs)
2014/08/22 20:00
Przykład dla regresji wielorakiej
Pewien wydawca książek chciał się dowiedzieć, jaki wpływ na zysk brutto ze sprzedaży mają takie zmienne jak: koszty produkcji, koszty reklamy, koszty promocji bezpośredniej, suma udzielonych rabatów, popularność autora. W tym celu przeanalizował 40 pozycji wydanych w ciągu ostatniego roku (zbiór uczący). Fragment danych przedstawia poniższy rysunek:
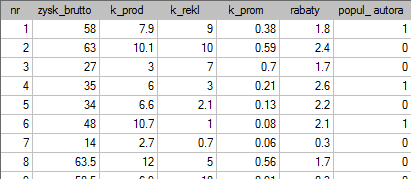
Pięć pierwszych zmiennych wyrażonych jest w tysiącach dolarów - są to więc zmienne zebrane na skali interwałowej. Natomiast ostatnia zmienna: popularność autora  to zmienna dychotomiczna, gdzie 1 oznacza autora znanego, 0 oznacza autora nieznanego.
to zmienna dychotomiczna, gdzie 1 oznacza autora znanego, 0 oznacza autora nieznanego.
Na podstawie uzyskanej wiedzy wydawca planuje przewidzieć zysk brutto z kolejnej wydawanej książki znanego autora. Koszty, jakie zamierza ponieść to: koszty produkcji 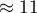 , koszty reklamy
, koszty reklamy 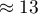 , koszty promocji bezpośredniej
, koszty promocji bezpośredniej 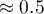 , suma udzielonych rabatów
, suma udzielonych rabatów 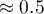 .
.
Budujemy model liniowej regresji wielorakiej dla zbioru uczącego wybierając: zysk brutto  jako zmienną zależną
jako zmienną zależną  , koszty produkcji, koszty reklamy, koszty promocji bezpośredniej, suma udzielonych rabatów, popularność autora
, koszty produkcji, koszty reklamy, koszty promocji bezpośredniej, suma udzielonych rabatów, popularność autora  jako zmienne niezależne
jako zmienne niezależne 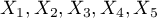 . W rezultacie wyliczone zostaną współczynniki równania regresji oraz miary pozwalające ocenić jakość modelu.
. W rezultacie wyliczone zostaną współczynniki równania regresji oraz miary pozwalające ocenić jakość modelu.
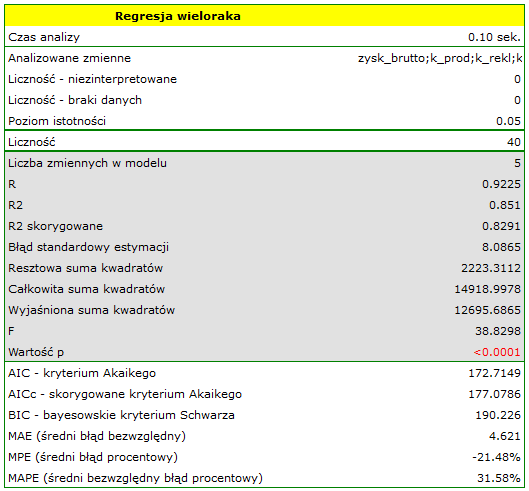
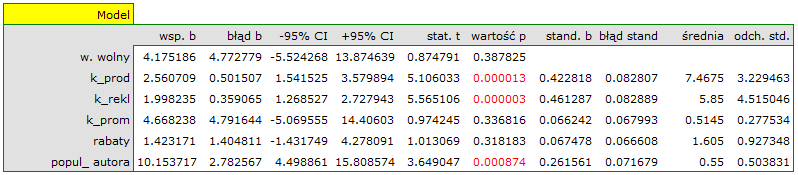
Na podstawie oszacowanej wartości współczynnika  , związek pomiędzy zyskiem brutto a wszystkimi zmiennymi niezależnymi możemy opisać równaniem:
, związek pomiędzy zyskiem brutto a wszystkimi zmiennymi niezależnymi możemy opisać równaniem:
![LaTeX \begin{displaymath}
zysk_{brutto}=4.18+2.56(k_{prod})+2(k_{rekl})+4.67(k_{prom})+1.42(rabaty)+10.15(popul_{autora})+[8.09]
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/imgf922fff467cfbd2ba68883ee92814649.png) Uzyskane współczynniki interpretujemy następująco:
Uzyskane współczynniki interpretujemy następująco:
- Jeśli koszt produkcji wzrośnie o 1 tysiąc dolarów, to zysk brutto wzrośnie o około 2.56 tysiące dolarów, przy złożeniu, że pozostałe zmienne się nie zmienią;
- Jeśli koszt reklamy wzrośnie o 1 tysiąc dolarów, to zysk brutto wzrośnie o około 2 tysiące dolarów, przy złożeniu, że pozostałe zmienne się nie zmienią;
- Jeśli koszt promocji bezpośredniej wzrośnie o 1 tysiąc dolarów, to zysk brutto wzrośnie o około 4.67 tysiące dolarów, przy złożeniu, że pozostałe zmienne się nie zmienią;
- Jeśli suma udzielonych rabatów wzrośnie o 1 tysiąc dolarów, to zysk brutto wzrośnie o około 1.42 tysiące dolarów, przy złożeniu, że pozostałe zmienne się nie zmienią;
- Jeśli książka została napisana przez autora znanego (oznaczonego przez 1), to w modelu popularność autora przyjmujemy jako wartość 1 i otrzymujemy równanie:
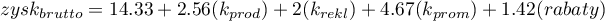 Jeśli natomiast książka została napisana przez autora nieznanego (oznaczonego przez 0), to w modelu popularność autora przyjmujemy jako wartość 0 i otrzymujemy równanie:
Jeśli natomiast książka została napisana przez autora nieznanego (oznaczonego przez 0), to w modelu popularność autora przyjmujemy jako wartość 0 i otrzymujemy równanie:
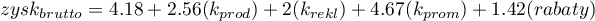 Wynik testu t-Studenta uzyskany dla każdej zmiennej wskazuje, że tylko koszt produkcji, koszt reklamy oraz popularność autora wywiera istotny wpływ na otrzymany zysk. Jednocześnie, dla tych zmiennych standaryzowane współczynniki
Wynik testu t-Studenta uzyskany dla każdej zmiennej wskazuje, że tylko koszt produkcji, koszt reklamy oraz popularność autora wywiera istotny wpływ na otrzymany zysk. Jednocześnie, dla tych zmiennych standaryzowane współczynniki  są największe.
są największe.
Dodatkowo, model jest dobrze dopasowany o czym świadczy: mały błąd standardowy estymacji 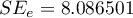 , wysoka wartość współczynnika determinacji wielorakiej
, wysoka wartość współczynnika determinacji wielorakiej 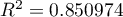 i poprawionego współczynnika determinacji wielorakiej
i poprawionego współczynnika determinacji wielorakiej 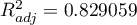 oraz wynik testu F analizy wariancji:
oraz wynik testu F analizy wariancji: 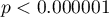 .
.
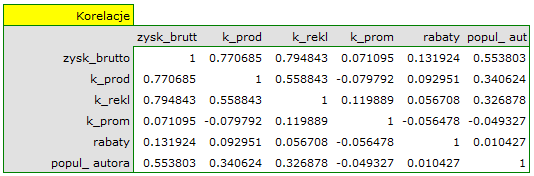
Na podstawie interpretacji dotychczasowych wyników możemy przypuszczać, że część zmiennych nie wywiera istotnego wpływu na zysk i może być zbyteczna. Aby model był dobrze sformułowany interwałowe zmienne niezależne powinny być silnie skorelowane ze zmienną zależną i stosunkowo słabo pomiędzy sobą. Możemy to sprawdzić wyliczając macierz korelacji i macierz kowariancji:
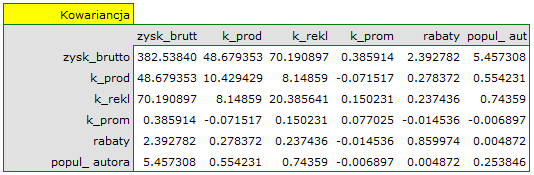
Najbardziej spójną informację, pozwalającą znaleźć te zmienne w modelu, które są zbędne (nadmiarowe) niesie analiza korelacji cząstkowej i semicząstkowej i nadmiarowości:
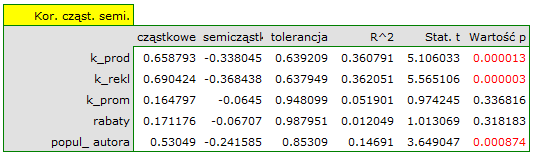
Wartości współczynników korelacji cząstkowej i semicząstkowej wskazują, że najmniejszy wkład w budowany model mają: koszt promocji bezpośredniej i suma udzielonych rabatów. Jednak, są to zmienne najmniej skorelowane z pozostałymi w modelu, o czym świadczy niska wartość  i wysoka wartość tolerancji. Ostatecznie, ze statystycznego punktu widzenia, modele bez tych zmiennych nie były by modelami gorszymi niż model obecny (patrz wynik testu t-Studenta dla porównywania modeli). To od decyzji badacza zależy, czy pozostawi ten model, czy zbuduje nowy model pozbawiony kosztów promocji bezpośredniej i sumy udzielonych rabatów. My pozostawiamy model obecny.
i wysoka wartość tolerancji. Ostatecznie, ze statystycznego punktu widzenia, modele bez tych zmiennych nie były by modelami gorszymi niż model obecny (patrz wynik testu t-Studenta dla porównywania modeli). To od decyzji badacza zależy, czy pozostawi ten model, czy zbuduje nowy model pozbawiony kosztów promocji bezpośredniej i sumy udzielonych rabatów. My pozostawiamy model obecny.
Na koniec przeprowadzimy analizę reszt. Fragment tej analizy znajduje się poniżej:
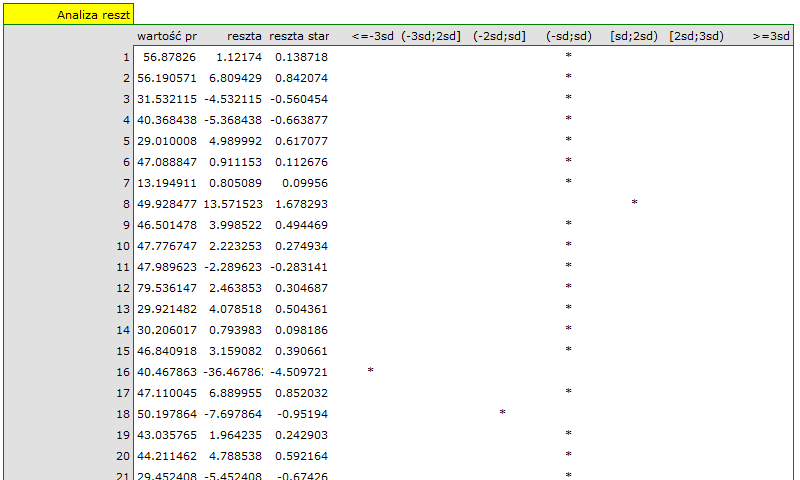
Możemy zauważyć, że jedna z reszt modelu jest obserwacją odstającą  jest oddalona o więcej niż 3 odchylenia standardowe od wartości średniej. Jest to obserwacja o numerze 16. Obserwację te możemy łatwo znaleźć kreśląc wykres resz względem obserwowanych lub przewidywanych wartości zmiennej
jest oddalona o więcej niż 3 odchylenia standardowe od wartości średniej. Jest to obserwacja o numerze 16. Obserwację te możemy łatwo znaleźć kreśląc wykres resz względem obserwowanych lub przewidywanych wartości zmiennej  .
.
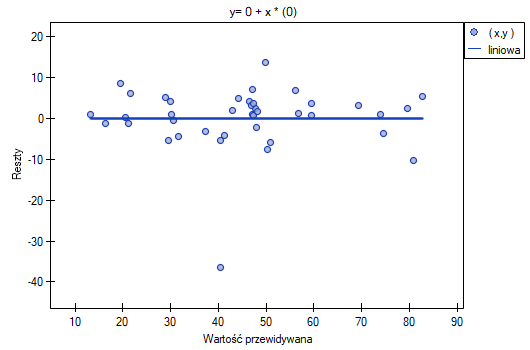
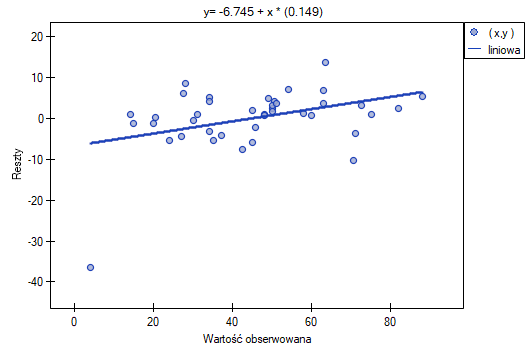
Ten odstający punkt zaburza założenie dotyczące homoskedastyczności. Założenie homoskedastyczności było by spełnione (tzn. wariancja reszt opisana na osi  byłaby podobna, gdy przechodzimy wzdłuż osi
byłaby podobna, gdy przechodzimy wzdłuż osi  ), gdybyśmy ten punkt odrzucili. Dodatkowo, rozkład reszt nieco odbiega od rozkładu normalnego (wartość
), gdybyśmy ten punkt odrzucili. Dodatkowo, rozkład reszt nieco odbiega od rozkładu normalnego (wartość  testu Lilieforsa wynosi
testu Lilieforsa wynosi 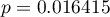 ):
):

Przyglądając się dokładniej punktowi odstającemu (pozycja 16 w danych do zadania) widzimy, że książka ta jako jedyna wykazuje wyższe koszty niż zysk brutto (zysk brutto = 4 tysiące dolarów, suma kosztów = (8+6+0.33+1.6) = 15.93 tysiące dolarów).
Uzyskany model możemy poprawić usuwając z niego punkt odstający. Wymaga to ponownego przeprowadzenia analizy z włączonym filtrem wykluczającym punkt odstający.
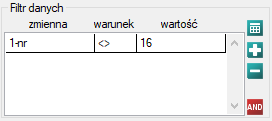
W rezultacie uzyskaliśmy bardzo podobny model, ale obarczony mniejszym błędem i lepiej dopasowany:
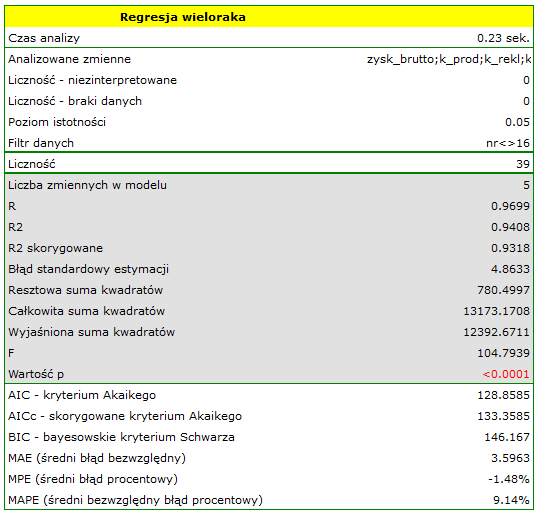
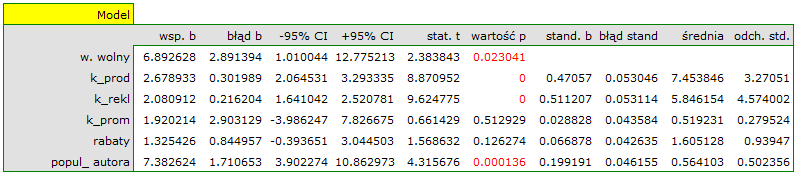
![LaTeX \begin{displaymath}
zysk_{brutto}=6.89+2.68(k_{prod})+2.08(k_{rekl})+1.92(k_{prom})+1.33(rabaty)+7.38(popul_{autora})+[4.86]
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img56f860f403564778be635c59de60dd63.png) Ostatecznie zbudowany model wykorzystamy do predykcji. Na podstawie przewidywanych nakładów w wysokości:
koszty produkcji
Ostatecznie zbudowany model wykorzystamy do predykcji. Na podstawie przewidywanych nakładów w wysokości:
koszty produkcji 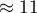 tysięcy dolarów,
koszty reklamy
tysięcy dolarów,
koszty reklamy 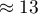 tysięcy dolarów,
koszty promocji bezpośredniej
tysięcy dolarów,
koszty promocji bezpośredniej 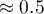 tysiąca dolarów,
suma udzielonych rabatów
tysiąca dolarów,
suma udzielonych rabatów 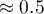 tysiąca dolarów,\\oraz faktu, że jest to autor znany (popularność autora
tysiąca dolarów,\\oraz faktu, że jest to autor znany (popularność autora 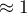 ) wyliczamy przewidywany zysk brutto wraz z przedziałem ufności:
) wyliczamy przewidywany zysk brutto wraz z przedziałem ufności:
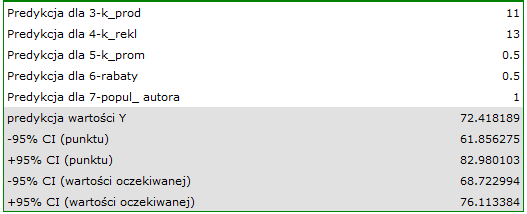
Przewidziany zysk wynosi 72 tysiące dolarów.
Na koniec należy jeszcze zauważyć, że jest to tylko model wstępny. W badaniu właściwym należałoby zebrać więcej danych. Liczba zmiennych w modelu jest bowiem zbyt mała w stosunku do liczby ocenianych książek tzn. n<50+8k
2021/01/11 22:01
Predykcja na podstawie modelu i walidacja zbioru testowego
Walidacja
Walidacja modelu to sprawdzenie jego jakości. W pierwszej kolejności wykonywana jest na danych, na których model był zbudowany (tzw. zbiór uczący), czyli zwracana jest w raporcie opisującym uzyskany model. By można było z większą pewnością osądzić na ile model nadaje się do prognozy nowych danych, ważnym elementem walidacji jest zostanie modelu do danych, które nie były wykorzystywane w estymacji modelu. Jeśli podsumowanie w oparciu o dane uczące będzie satysfakcjonujące tzn. wyznaczane błędy, współczynniki  i kryteria informacyjne będą na zadowalającym nas poziomie, a podsumowanie w oparciu o nowe dane (tzw. zbiór testowy) będzie równie korzystne, wówczas z dużym prawdopodobieństwem można uznać, że taki model nadaje się do predykcji. Dane testujące powinny pochodzić z tej samej populacji, z której były wybrane dane uczące. Często jest tak, że przed przystąpieniem do budowy modelu zbieramy dane, a następnie w sposób losowy dzielimy je na zbiór uczący, czyli dane które posłużą do budowy modelu i zbiór testowy, czyli dane które posłużą do dodatkowej walidacji modelu.
i kryteria informacyjne będą na zadowalającym nas poziomie, a podsumowanie w oparciu o nowe dane (tzw. zbiór testowy) będzie równie korzystne, wówczas z dużym prawdopodobieństwem można uznać, że taki model nadaje się do predykcji. Dane testujące powinny pochodzić z tej samej populacji, z której były wybrane dane uczące. Często jest tak, że przed przystąpieniem do budowy modelu zbieramy dane, a następnie w sposób losowy dzielimy je na zbiór uczący, czyli dane które posłużą do budowy modelu i zbiór testowy, czyli dane które posłużą do dodatkowej walidacji modelu.
Okno z ustawieniami opcji walidacji wywołujemy poprzez menu Statystyki zaawansowane→Modele wielowymiarowe→Regresja wieloraka - predykcja/walidacja.
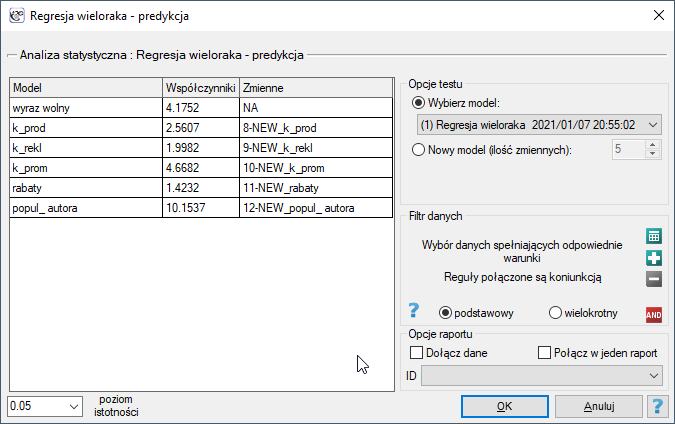
By dokonać walidacji należy wskazać model, na podstawie którego chcemy jej dokonać. Walidacji możemy dokonać na bazie:
- zbudowanego w PQStat modelu regresji wielorakiej - wystarczy wybrać model spośród modeli przypisanych do danego arkusza, a liczba zmiennych i współczynniki modelu zostaną ustawione automatycznie; zbiór testowy powinien się znaleźć w tym samym arkuszu co zbiór uczący;
- modelu niezbudowanego w programie PQStat ale uzyskanego z innego źródła (np. opisanego w przeczytanej przez nas pracy naukowej) - w oknie analizy należy podać liczbę zmiennych oraz wpisać współczynniki dotyczące każdej z nich.
W oknie analizy należy wskazać te nowe zmienne, które powinny zostać wykorzystane do walidacji.
Predykcja
Najczęściej ostatnim etapem analizy regresji jest wykorzystanie zbudowanego i uprzednio zweryfikowanego modelu do predykcji.
- Predykcja dla jednego obiektu może być wykonywana wraz z budową modelu, czyli w oknie analizy
Statystyki zaawansowane→Modele wielowymiarowe→Regresja wieloraka, - Predykcja dla większej grupy nowych danych jest wykonywana poprzez menu
Statystyki zaawansowane→Modele wielowymiarowe→Regresja wieloraka - predykcja/walidacja.
By dokonać predykcji należy wskazać model, na podstawie którego chcemy jej dokonać. Predykcji możemy dokonać na bazie:
- zbudowanego w PQStat modelu regresji wielorakiej - wystarczy wybrać model spośród modeli przypisanych do danego arkusza, a liczba zmiennych i współczynniki modelu zostaną ustawione automatycznie; zbiór testowy powinien się znaleźć w tym samym arkuszu co zbiór uczący;
- modelu niezbudowanego w programie PQStat ale uzyskanego z innego źródła (np. opisanego w przeczytanej przez nas pracy naukowej) - w oknie analizy należy podać liczbę zmiennych oraz wpisać współczynniki dotyczące każdej z nich.
W oknie analizy należy wskazać te nowe zmienne, które powinny zostać wykorzystane do predykcji. Oszacowana wartość wyliczana jest z pewnym błędem. Dlatego też dodatkowo dla przewidzianej przez model wartości wyznaczane są granice wynikające z błędu:
- dla wartości oczekiwanej wyznaczane są granice ufności,
- dla pojedynczego punktu wyznaczane są granice predykcji.
Przykład c.d. (plik wydawca.pqs)
Do przewidywania zysku brutto ze sprzedaży książek wydawca zbudował model regresji w oparciu o zbiór uczący pozbawiony pozycji 16 (czyli 39 książek). W modelu znalazły się: koszty produkcji, koszty reklamy i popularność autora (1=autor popularny, 0=nie). Zbudujemy raz jeszcze ten model w oparciu zbiór uczący a następnie, by się upewnić, że model będzie działał poprawnie, zwalidujemy go na testowym zbierze danych. Jeśli model przejdzie tę próbę, to będziemy go stosować do predykcji dla pozycji książkowych. By korzystać z odpowiednich zbiorów ustawiamy każdorazowo filtr danych.
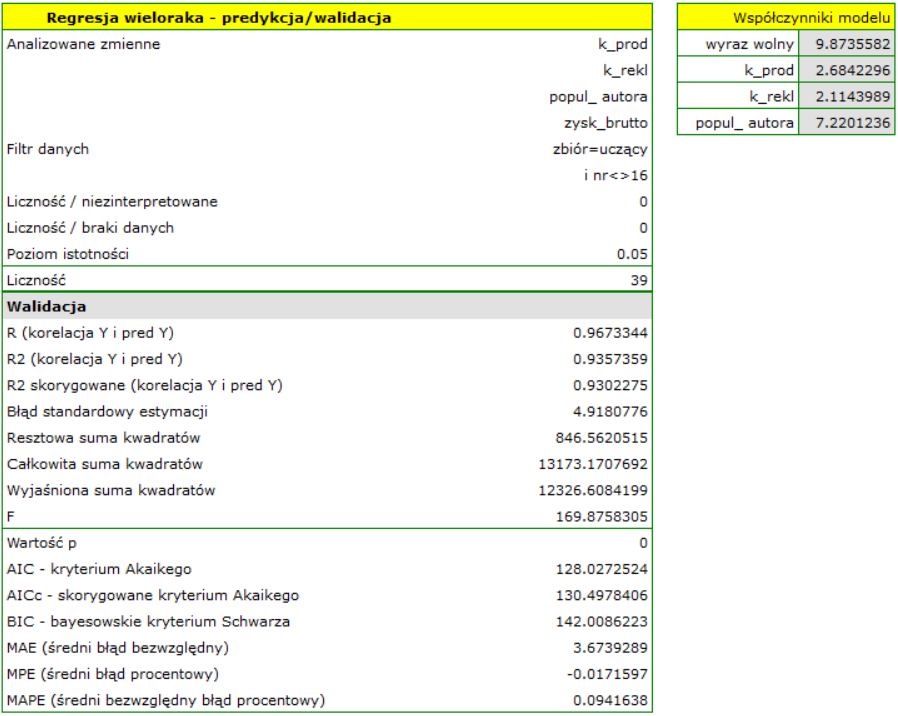
Dla zbioru uczącego wartości opisujące jakość dopasowania modelu są bardzo wysokie: skorygowane  = 0.93 a średni błąd prognozy (MAE) wynosi 3.8 tys. dolarów.
= 0.93 a średni błąd prognozy (MAE) wynosi 3.8 tys. dolarów.
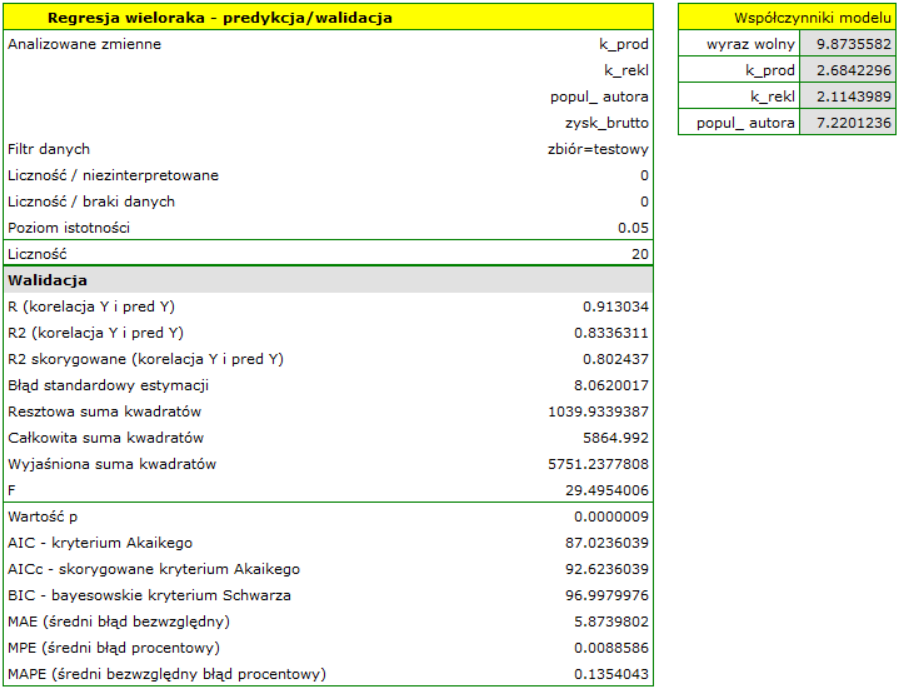
Dla zbioru testowego wartości opisujące jakość dopasowania modelu są nieco niższe niż dla zbioru uczącego: Skorygowane  = 0.80 a średni błąd prognozy (MAE) wynosi 5.9 tys. dolarów. Ponieważ wynik walidacji na zbiorze testowym jest prawie tak dobry jak na zbiorze uczącym, użyjemy modelu do predykcji. W tym celu skorzystamy z danych trzech nowych pozycji książkowych dopisanych na końcu zbioru. Wybierzemy opcję
= 0.80 a średni błąd prognozy (MAE) wynosi 5.9 tys. dolarów. Ponieważ wynik walidacji na zbiorze testowym jest prawie tak dobry jak na zbiorze uczącym, użyjemy modelu do predykcji. W tym celu skorzystamy z danych trzech nowych pozycji książkowych dopisanych na końcu zbioru. Wybierzemy opcję Predykcja, ustawiany filtr na nowy zbiór danych i użyjemy naszego modelu do tego by przewidzieć zysk brutto dla tych książek.
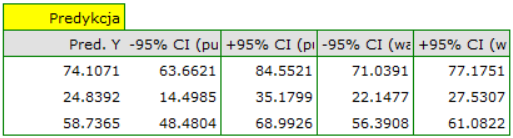
Okazuje się, że najwyższy zysk brutto (pomiędzy 64 a 85 tys. dolarów) jest prognozowany dla pierwszej, najbardziej reklamowanej i najdrożej wydanej książki popularnego autora.
2014/08/22 20:00
2014/08/22 20:00
Porównywanie modeli liniowej regresji wielorakiej
Okno z ustawieniami opcji porównywania modeli wywołujemy poprzez menu Statystyka→Modele wielowymiarowe→Regresja wieloraka - porównywanie modeli
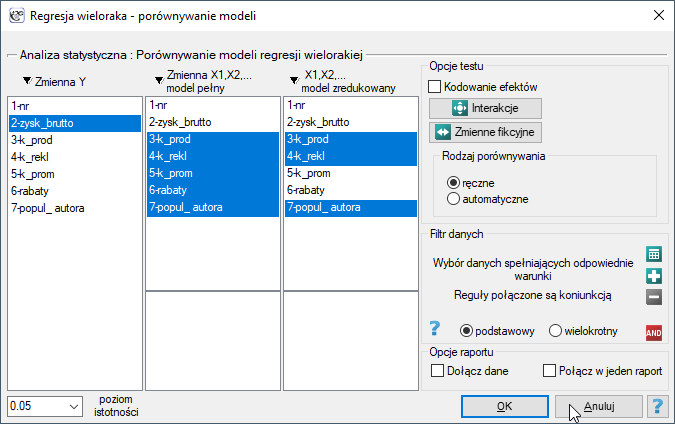
Liniowa regresja wieloraka daje możliwość jednoczesnej analizy wielu zmiennych niezależnych. Pojawia się więc problem wyboru optymalnego modelu. W natłoku informacji jakie niesie zbyt duży model istnieje możliwość zagubienia ważnych informacji. Zbyt mały może pominąć te cechy, które w wiarygodny sposób mogłyby opisać badane zjawisko. Bowiem nie liczba zmiennych w modelu, ale ich jakość decyduje o jakości modelu. W wyborze zmiennych niezależnych niezbędna jest wiedza i doświadczenie związane z badanym zjawiskiem. Należy pamiętać, by w modelu znajdowały się zmienne silnie skorelowane ze zmienną zależną i słabo skorelowane między sobą.
Nie istnieje jedna prosta reguła statystyczna, która decydowałaby o liczbie zmiennych niezbędnych w modelu. Najczęściej w porównaniu posługujemy się miarami dopasowania modelu takimi jak: 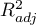 - poprawiona wartość współczynnika determinacji wielorakiej (im wyższa wartość tym lepiej dopasowany model),
- poprawiona wartość współczynnika determinacji wielorakiej (im wyższa wartość tym lepiej dopasowany model), 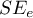 - błąd standardowy estymacji (im niższa wartość tym lepiej dopasowany model) lub kryteria informacyjne AIC, AICc, BIC (im niższa wartość tym lepszy model). W tym celu można również wykorzystać test F oparty o współczynnik determinacji wielorakiej
- błąd standardowy estymacji (im niższa wartość tym lepiej dopasowany model) lub kryteria informacyjne AIC, AICc, BIC (im niższa wartość tym lepszy model). W tym celu można również wykorzystać test F oparty o współczynnik determinacji wielorakiej  . Test ten służy do weryfikacji hipotezy, że dopasowanie obu porównywanych modeli jest tak samo dobre.
. Test ten służy do weryfikacji hipotezy, że dopasowanie obu porównywanych modeli jest tak samo dobre.
Hipotezy:
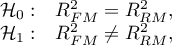
gdzie:
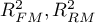
 współczynniki determinacji wielorakiej w porównywanych modelach (pełnym i zredukowanym).
współczynniki determinacji wielorakiej w porównywanych modelach (pełnym i zredukowanym).
Statystyka testowa ma postać:
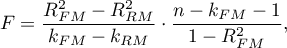
Statystyka ta podlega rozkładowi F Snedecora z 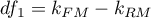 i
i 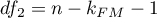 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica w jakości dopasowania modeli jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym  lub mniejszej wielkości kryterium informacyjnego) jest istotnie lepszy niż drugi.
lub mniejszej wielkości kryterium informacyjnego) jest istotnie lepszy niż drugi.
W programie PQStat porównywanie modeli możemy przeprowadzić ręcznie lub automatycznie.
- Ręczne porównywanie modeli- polega na zbudowaniu 2 modeli:
pełnego - modelu z większą liczbą zmiennych,
zredukowanego - modelu z mniejszą liczbą zmiennych  model taki powstaje z modelu pełnego po usunięciu zmiennych, które z punktu widzenia badanego zjawiska są zbędne.
model taki powstaje z modelu pełnego po usunięciu zmiennych, które z punktu widzenia badanego zjawiska są zbędne.
Wybór zmiennych niezależnych w porównywanych modelach a następnie wybór lepszego modelu, na podstawie uzyskanych wyników porównania, należy do badacza.
- Automatyczne porównywanie modeli jest wykonywane w kilku krokach:
[krok 1] Zbudowanie modelu z wszystkich zmiennych.
[krok 2] Usunięcie jednej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.
[krok 3] Porównanie modelu pełnego i zredukowanego.
[krok 4] Usunięcie kolejnej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.
[krok 5] Porównanie modelu wcześniejszego i nowo zredukowanego.
[…]
W ten sposób powstaje wiele, coraz mniejszych modeli. Ostatni model zawiera tylko 1 zmienną niezależną.
W rezultacie, każdy model jest opisany miarami dopasowania (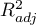 ,
, 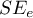 , AIC, AICc, BIC), a kolejno powstające (sąsiednie) modele są porównywane testem F. Model, który zostanie ostatecznie zaznaczony jako statystycznie optymalny, to model o największym
, AIC, AICc, BIC), a kolejno powstające (sąsiednie) modele są porównywane testem F. Model, który zostanie ostatecznie zaznaczony jako statystycznie optymalny, to model o największym 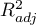 , najmniejszym kryterium informacyjnym i najmniejszym
, najmniejszym kryterium informacyjnym i najmniejszym 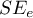 . Ponieważ jednak żadna z metod statystycznych nie potrafi w pełni odpowiedzieć na pytanie który z modeli jest najlepszy, to badacz, na podstawie uzyskanych wyników, powinien wybrać model.
. Ponieważ jednak żadna z metod statystycznych nie potrafi w pełni odpowiedzieć na pytanie który z modeli jest najlepszy, to badacz, na podstawie uzyskanych wyników, powinien wybrać model.
Przykład c.d. (plik wydawca.pqs)
Do przewidywania zysku brutto ze sprzedaży książek wydawca planuje brać pod uwagę takie zmienne jak: koszty produkcji, koszty reklamy, koszty promocji bezpośredniej, suma udzielonych rabatów, popularność autora. Nie wszystkie te zmienne muszą jednak wpływać znacząco na zysk. Spróbujemy wybrać taki model regresji liniowej, który będzie zawierał optymalną (ze statystycznego punktu widzenia) liczbę zmiennych. Do tej analizy użyjemy danych zbioru uczącego.
- Ręczne porównywanie modeli.
Na podstawie zbudowanego wcześniej modelu pełnego możemy podejrzewać, że zmienne: koszty promocji bezpośredniej, suma udzielonych rabatów mają niewielki wpływ na budowany model (tzn. te zmienne nie pomagają przewidzieć wielkości zysku). Sprawdzimy czy, ze statystycznego punktu widzenia, model pełny jest lepszy niż model po usunięciu tych dwóch zmiennych.
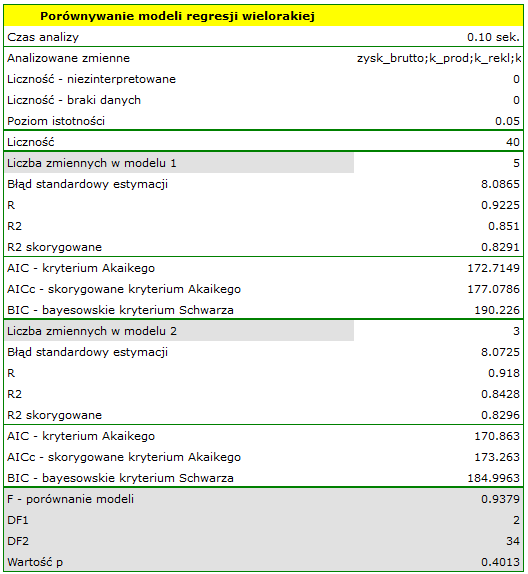
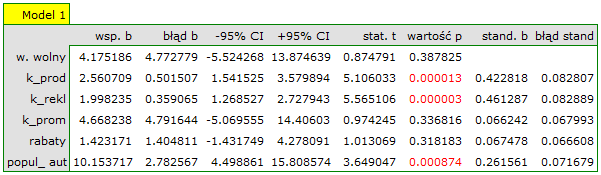
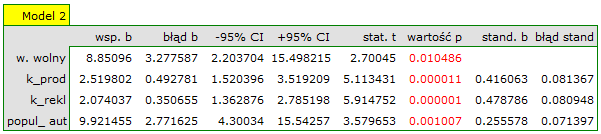
Okazuje się, że nie ma podstaw by uważać, że model pełny jest lepszy niż model zredukowany (wartość  testu F służącego porównywaniu modeli wynosi
testu F służącego porównywaniu modeli wynosi  ). Dodatkowo, model zredukowany jest nieco lepiej dopasowany niż model pełny (dla modelu zredukowanego
). Dodatkowo, model zredukowany jest nieco lepiej dopasowany niż model pełny (dla modelu zredukowanego 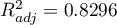 , dla modelu pełnego
, dla modelu pełnego 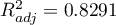 ) oraz ma mniejsze, czyli korzystniejsze wartości kryteriów informacyjnych AIC, AICc i BIC.
) oraz ma mniejsze, czyli korzystniejsze wartości kryteriów informacyjnych AIC, AICc i BIC.
- Automatyczne porównywanie modeli.
W przypadku automatycznego porównywania modeli uzyskaliśmy bardzo podobne wyniki. Najlepszym modelem jest model o największym współczynniku 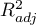 , najmniejszych kryteriach informacyjnych i najmniejszym błędzie standardowym estymacji
, najmniejszych kryteriach informacyjnych i najmniejszym błędzie standardowym estymacji 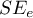 . Sugerowanym najlepszym modelem jest tu model zawierający tylko 3 zmienne niezależne: koszty produkcji, koszty reklamy, popularność autora.
Na podstawie powyższych analiz, ze statystycznego punktu widzenia, optymalnym modelem jest model zawierający 3 najważniejsze zmienne niezależne: koszty produkcji, koszty reklamy, popularność autora. Jednak ostateczna decyzja, który model wybrać należy do osoby posiadającą specjalistyczną widzę z zakresu badania - w tym przypadku wydawcy. Należy pamiętać, że wybrany model powinien zostać ponownie zbudowany a jego założenia zweryfikowane w oknie
. Sugerowanym najlepszym modelem jest tu model zawierający tylko 3 zmienne niezależne: koszty produkcji, koszty reklamy, popularność autora.
Na podstawie powyższych analiz, ze statystycznego punktu widzenia, optymalnym modelem jest model zawierający 3 najważniejsze zmienne niezależne: koszty produkcji, koszty reklamy, popularność autora. Jednak ostateczna decyzja, który model wybrać należy do osoby posiadającą specjalistyczną widzę z zakresu badania - w tym przypadku wydawcy. Należy pamiętać, że wybrany model powinien zostać ponownie zbudowany a jego założenia zweryfikowane w oknie Regresja wieloraka.
2014/08/22 20:00
Regresja logistyczna
Okno z ustawieniami opcji Regresji logistycznej wywołujemy poprzez menu Statystyka zaawansowana→Modele wielowymiarowe→Regresja logistyczna
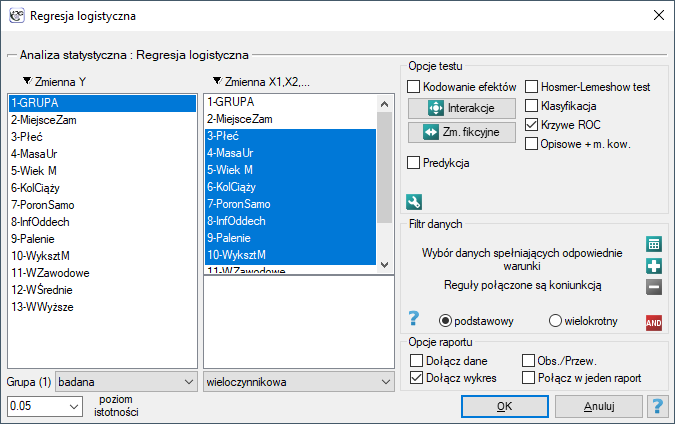

 Budowany model regresji logistycznej (podobnie jak liniowej regresji wielorakiej) pozwala na zbadanie wpływu wielu zmiennych niezależnych (
Budowany model regresji logistycznej (podobnie jak liniowej regresji wielorakiej) pozwala na zbadanie wpływu wielu zmiennych niezależnych (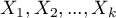 ) na jedną zmienną zależną (
) na jedną zmienną zależną ( ). Tym razem jednak zmienna zależna przyjmuje jedynie dwie wartości, np. chory/zdrowy, niewypłacalny/wypłacalny itp.
). Tym razem jednak zmienna zależna przyjmuje jedynie dwie wartości, np. chory/zdrowy, niewypłacalny/wypłacalny itp.
Owe dwie wartości kodowane są jako (1)/(0) gdzie:
(1) wartość wyróżniona - posiadanie danej cechy
(0) brak danej cechy.
Funkcja, na której oparty jest model regresji logistycznej wylicza nie dwupoziomową zmienną  , a prawdopodobieństwo przyjęcia przez tą zmienną wyróżnionej wartości:
, a prawdopodobieństwo przyjęcia przez tą zmienną wyróżnionej wartości:
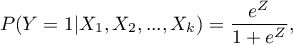 gdzie:
gdzie:
 prawdopodobieństwo przyjęcia wartości wyróżnionej (1) pod warunkiem uzyskania konkretnych wartości zmiennych niezależnych, tzw. prawdopodobieństwo przewidywane dla 1.
prawdopodobieństwo przyjęcia wartości wyróżnionej (1) pod warunkiem uzyskania konkretnych wartości zmiennych niezależnych, tzw. prawdopodobieństwo przewidywane dla 1.
 najczęściej wyrażone jest zależnością liniową:
najczęściej wyrażone jest zależnością liniową:
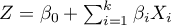 ,
,
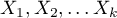 - zmienne niezależne, objaśniające,
- zmienne niezależne, objaśniające,
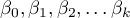 - parametry.
- parametry.
Zmienne fikcyjne i interakcje w modelu
Omówienie przygotowania zmiennych fikcyjnych i interakcji przedstawiono w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
Uwaga!
Funkcja Z może być również opisana zależnością wyższego stopnia np. kwadratową - do modelu wprowadzamy wówczas zmienną zawierającą kwadrat danej zmiennej niezależnej 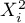 .
.
Logitem nazywamy przekształcenie tego modelu do postaci:
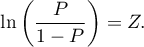
Macierze biorące udział w równaniu, dla próby o liczności  , zapisujemy następująco:
, zapisujemy następująco:
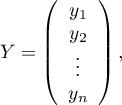

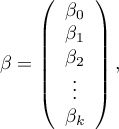
Rozwiązaniem równania jest wówczas wektor ocen parametrów  nazywanych współczynnikami regresji:
nazywanych współczynnikami regresji:
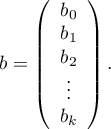
Współczynniki te szacowane są poprzez metodę największej wiarygodności czyli poprzez poszukiwanie maksimum funkcji wiarygodności 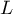 (w programie użyto algorytm iteracyjny Newton-Raphson) . Na podstawie tych wartości możemy wnioskować o wielkości wpływu zmiennej niezależnej (dla której ten współczynnik został oszacowany) na zmienną zależną.
(w programie użyto algorytm iteracyjny Newton-Raphson) . Na podstawie tych wartości możemy wnioskować o wielkości wpływu zmiennej niezależnej (dla której ten współczynnik został oszacowany) na zmienną zależną.
Każdy współczynnik obarczony jest pewnym błędem szacunku. Wielkość tego błędu wyliczana jest ze wzoru:
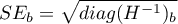 gdzie:
gdzie:
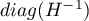 to główna przekątna macierzy kowariancji.
to główna przekątna macierzy kowariancji.
Uwaga!
Budując model należy pamiętać, że liczba obserwacji powinna być przynajmniej dziesięciokrotnie większa lub równa liczbie szacowanych parametrów modelu (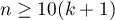 ). Jednak, coraz częściej stosuje się bardziej restrykcyjne kryterium zaproponowane przez P. Peduzzi i innych w roku 1996 8) mówiące, iż liczba obserwacji powinna być dziesięciokrotnie większa lub równa stosunkowi liczby zmiennych niezależnych (
). Jednak, coraz częściej stosuje się bardziej restrykcyjne kryterium zaproponowane przez P. Peduzzi i innych w roku 1996 8) mówiące, iż liczba obserwacji powinna być dziesięciokrotnie większa lub równa stosunkowi liczby zmiennych niezależnych ( ) i mniejszej z proporcji liczności (
) i mniejszej z proporcji liczności ( ) opisanych z zmiennej zależnej (tzn. propoprcji chorych lub zdrowych), czyli (
) opisanych z zmiennej zależnej (tzn. propoprcji chorych lub zdrowych), czyli (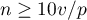 ).
).
Uwaga! Budując model należy pamiętać, że zmienne niezależne nie powinny być współliniowe. W przypadku gdy występuje współliniowość, estymacja może być niepewna a uzyskane wartości błędów bardzo wysokie. Zmienne współliniowe należy usunąć z modelu bądź zbudować z nich jedną zmienna niezależną np. zamiast współliniowych zmiennych: wiek matki i wiek ojca można zbudować zmienną wiek rodziców.
Uwaga! Kryterium zbieżności funkcji algorytmu iteracyjnego Newtona-Raphsona można kontrolować przy pomocy dwóch parametrów: limitu iteracji zbieżności (podaje maksymalną ilość iteracji w jakiej algorytm powinien osiągnąć zbieżność) i kryterium zbieżności (podaje wartość poniżej której uzyskana poprawa estymacji uznana będzie za nieznaczną i algorytm zakończy działanie).
Iloraz Szans
Jednostkowy Iloraz Szans
Na podstawie współczynników, dla każdej zmiennej niezależnej w modelu, wylicza się łatwą w interpretacji miarę jaką jest jednostkowy Iloraz Szans:
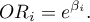
Otrzymany Iloraz Szans wyraża zmianę szansy na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna rośnie o 1 jednostkę. Wynik ten jest skorygowany o pozostałe zmienne niezależne znajdujące się w modelu w ten sposób, że zakłada iż pozostają one na stałym poziomie podczas, gdy badana zmienna niezależna rośnie o jednostkę.
Wartość OR interpretujemy następująco:
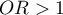 oznacza stymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile wzrasta szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.
oznacza stymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile wzrasta szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.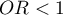 oznacza destymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile spada szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.
oznacza destymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile spada szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.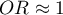 oznacza, że badana zmienna niezależna nie ma wpływu na uzyskanie wyróżnionej wartości (1).
oznacza, że badana zmienna niezależna nie ma wpływu na uzyskanie wyróżnionej wartości (1).
[Iloraz Szans - wzór ogólny]
Program PQStat wylicza jednostkowy Iloraz Szans. Jego modyfikacja, na podstawie ogólnego wzoru, umożliwia zmianę interpretacji uzyskanego wyniku.
Iloraz szans na wystąpienie stanu wyróżnionego w ogólnym przypadku jest wyliczany jako iloraz dwóch szans. Zatem dla zmiennej niezależnej  dla
dla  wyrażonego zależnością liniową wyliczamy:
wyrażonego zależnością liniową wyliczamy:
szansę dla kategorii pierwszej:
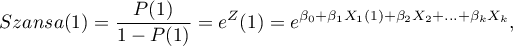
szansę dla kategorii drugiej:
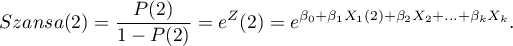
Iloraz Szans dla zmiennej  wyraża się wówczas wzorem:
wyraża się wówczas wzorem:
![LaTeX \begin{displaymath}
\begin{array}{lll}
OR_1(2)/(1) &=&\frac{Szansa(2)}{Szansa(1)}=\frac{e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k}}{e^{\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k}}\\
&=& e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k-[\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k]}\\
&=& e^{\beta_1X_1(2)-\beta_1X_1(1)}=e^{\beta_1[X_1(2)-X_1(1)]}=\\
&=& \left(e^{\beta_1}\right)^{[X_1(2)-X_1(1)]}.
\end{array}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img5e7d555cf6560897adceb6c87ea41a56.png)
Przykład
Jeśli zmienną niezależną jest wiek wyrażony w latach, to różnica pomiędzy sąsiadującymi kategoriami wieku np. 25 lat i 26 lat wynosi 1 rok 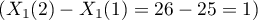 . Wówczas otrzymamy jednostkowy Iloraz Szans:
. Wówczas otrzymamy jednostkowy Iloraz Szans:
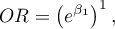 który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 1 rok.
który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 1 rok.
Iloraz szans wyliczony dla niesąsiadujących kategorii zmiennej wiek np. 25 lat i 30 lat będzie pięcioletnim Ilorazem Szans, ponieważ różnica 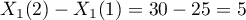 . Wówczas otrzymamy pięcioletni Iloraz Szans:
. Wówczas otrzymamy pięcioletni Iloraz Szans:
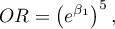 który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 5 lat.
który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 5 lat.
Uwaga!
Jeśli analizę przeprowadzamy dla modelu innego niż liniowy, lub uwzględniamy interakcję, wówczas na podstawie ogólnego wzoru możemy wyliczyć odpowiedni Ilorazu Szans zmieniając formułę wyrażającą  .
.
Przykład c.d. (plik zadanie.pqs)
Przykład c.d. (wada.pqs)
2014/08/22 20:00
Weryfikacja modelu
Istotność statystyczna poszczególnych zmiennych w modelu (istotność ilorazu szans)
Na podstawie współczynnika oraz jego błędu szacunku możemy wnioskować czy zmienna niezależna, dla której ten współczynnik został oszacowany wywiera istotny wpływ na zmienną zależną. W tym celu posługujemy się testem Walda.
Hipotezy:
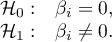 lub równoważnie:
lub równoważnie:
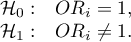
Statystykę testową testu Walda wyliczamy według wzoru:
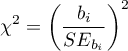 Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniem swobody .
stopniem swobody .
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Jakość zbudowanego modelu
Dobry model powinien spełniać dwa podstawowe warunki: powinien być dobrze dopasowany i możliwie jak najprostszy. Jakość modelu regresji logistycznej możemy ocenić kilkoma miarami, które opierają się na:
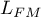 - maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
- maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
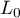 - maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
- maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
 - liczności próby.
- liczności próby.
- Kryteria informacyjne opierają się na entropii informacji niesionej przez model (niepewności modelu) tzn. szacują utraconą informację, gdy dany model jest używany do opisu badanego zjawiska. Powinniśmy zatem wybierać model o minimalnej wartości danego kryterium informacyjnego.
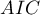 ,
, 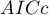 i
i 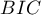 jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu (
jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu ( ) i liczności próby (
) i liczności próby ( ). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
- Kryterium informacyjne Akaikego (ang. Akaike information criterion)
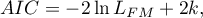
Jest to kryterium asymptotyczne - odpowiednie dla dużych prób.
- Poprawione kryterium informacyjne Akaikego
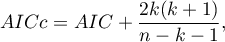
Poprawka kryterium Akaikego dotyczy wielkości próby, przez co jest to miara rekomendowana również dla prób o małych licznościach.
- Bayesowskie kryterium informacyjne Schwartza (ang. Bayes Information Criterion lub Schwarz criterion)
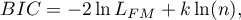
Podobnie jak poprawione kryterium Akaikego uwzględnia wielkość próby.
- Pseudo R
 - tzw. McFadden R
- tzw. McFadden R jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej
jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej  wyznaczanego dla liniowej regresji wielorakiej) .
wyznaczanego dla liniowej regresji wielorakiej) .
Wartość tego współczynnika mieści się w przedziale 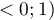 , gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu,
, gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu,  - zupełny bark dopasowania. Współczynnik
- zupełny bark dopasowania. Współczynnik 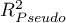 wyliczamy z wzoru:
wyliczamy z wzoru:
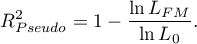
Ponieważ współczynnik 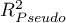 nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
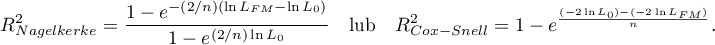
- Istotność statystyczna wszystkich zmiennych w modelu
Podstawowym narzędziem szacującym istotność wszystkich zmiennych w modelu jest test ilorazu wiarygodności. Test ten weryfikuje hipotezę:
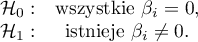
Statystyka testowa ma postać:
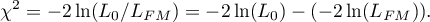
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Test Hosmera-Lemeshowa - Test ten, dla różnych podgrup danych, porównuje obserwowane liczności występowania wartości wyróżnionej
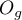 i przewidywane prawdopodobieństwo
i przewidywane prawdopodobieństwo 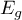 . Jeśli
. Jeśli 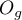 i
i 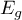 są wystarczająco bliskie, wówczas można założyć, że zbudowano dobrze dopasowany model.
są wystarczająco bliskie, wówczas można założyć, że zbudowano dobrze dopasowany model.
Do obliczeń najpierw obserwacje są dzielone na 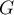 podgrup - zwykle na decyle (
podgrup - zwykle na decyle (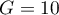 ).
).
Hipotezy:
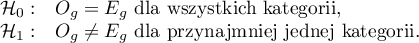
Statystyka testowa ma postać:
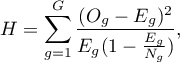 gdzie:
gdzie:
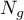 - liczba obserwacji w grupie
- liczba obserwacji w grupie 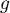 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 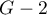 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

 AUC - pole pod krzywą ROC - Krzywa ROC, zbudowana w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo zmiennej zależnej
AUC - pole pod krzywą ROC - Krzywa ROC, zbudowana w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo zmiennej zależnej 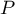 , pozwala na ocenę zdolności zbudowanego modelu regresji logistycznej do klasyfikacji przypadków do dwóch grup: (1) i (0). Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną modelu. Gdy krzywa ROC pokrywa się z przekątną
, pozwala na ocenę zdolności zbudowanego modelu regresji logistycznej do klasyfikacji przypadków do dwóch grup: (1) i (0). Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną modelu. Gdy krzywa ROC pokrywa się z przekątną  , to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej
, to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej  , czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą
, czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą  , zatem większe niż
, zatem większe niż 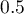
Hipotezy:
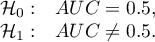
Statystyka testowa ma postać:
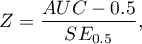 gdzie:
gdzie:
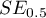 - błąd pola.
- błąd pola.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo, dla krzywej ROC podawana jest proponowana wartość punktu odcięcia prawdopodobieństwa przewidywanego, oraz tabela podająca wielkość czułości i swoistości dla każdego możliwego punktu odcięcia.
Uwaga! Więcej możliwości w wyliczeniu punktu odcięcia daje moduł **Krzywa ROC**. Analizę przeprowadzamy na podstawie wartości obserwowanych i prawdopodobieństwa przewidywanego, które uzyskujemy w analizie regresji logistycznej.
- Klasyfikacja
Na podstawie wybranego punktu odcięcia prawdopodobieństwa przewidywanego można sprawdzić jakość klasyfikacji. Punkt odcięcia, to domyślnie wartość 0.5. Użytkownik może zmienić tę wartość na dowolną wartość z przedziału 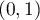 np. wartość sugerowaną przez krzywą ROC.
np. wartość sugerowaną przez krzywą ROC.
W wyniku uzyskamy tabelę klasyfikacji oraz procent poprawnie zaklasyfikowanych przypadków, procent poprawnie zaklasyfikowanych (0) - swoistość oraz procent poprawnie zaklasyfikowanych (1) - czułość.
2014/08/22 20:00
Wykresy w regresji logistycznej
- Iloraz szans i przedział ufności - to wykres przedstawiający OR wraz z 95% przedziałem ufności dla wyniku każdej zmiennej zwróconej w zbudowanym modelu. Dla zmiennych kategorialnych, linia na poziomie 1 wskazuje wartość ilorazu szans dla kategorii referencyjnej.
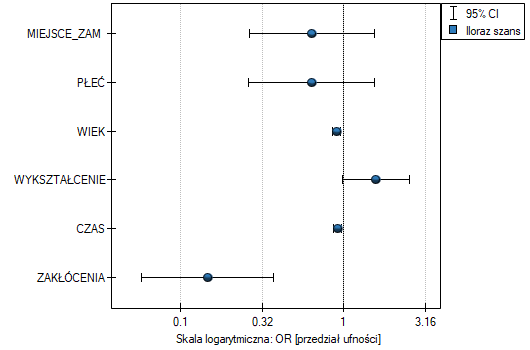
- Wartości obserwowane / Prawdopodobieństwo oczekiwane - to wykres przedstawiający wyniki przewidywanego dla każdej osoby prawdopodobieństwa wystąpienia zdarzenia (oś X) oraz wartości prawdziwej, czyli wystąpienia zdarzenia (wartość 1 na osi Y) lub braku zdarzenia (wartość 0 na osi Y). Jeśli model bardzo dobrze prognozuje, to przy lewej stronie wykresu punkty będą się kumulowały w dolnej części, a przy prawej stronie wykresu w górnej części.
- Krzywa ROC - to wykres zbudowany w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo wystąpienia zdarzenia.
- Wykres reszt Pearsona - to wykres pozwalający ocenić czy występują odstające dane. Reszty to różnice wartości obserwowanej i przewidywanego przez model prawdopodobieństwa. Wykresy surowych reszt z regresji logistycznej trudno interpretować, dlatego ujednolica się je wyznaczając reszty Pearsona. Reszta Pearsona to surowa reszta podzielona przez pierwiastek kwadratowy z funkcji wariancji. Znak (dodatni lub ujemny) wskazuje, czy obserwowana wartość jest wyższa, czy niższa niż wartość dopasowana do modelu, a wielkość wskazuje stopień odchylenia. Reszty Persona mniejsze lub większe niż 3 sugerują, zbyt duże odchylenie danego obiektu.
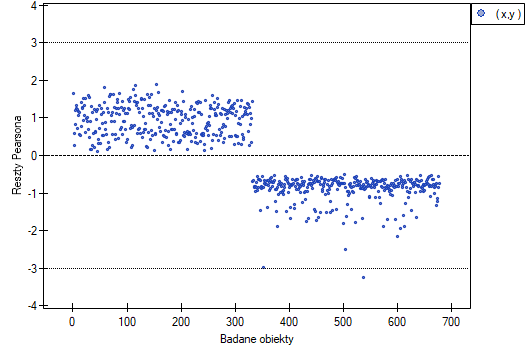
- Jednostkowe zmiany ilorazu szans - to wykres przedstawiający serie ilorazów szans wraz z przedziałem ufności, wyznaczane dla każdego z możliwych punktów odcięcia zmiennej umieszczonej na osi X. Umożliwia on użytkownikowi wybór jednego, dobrego punktu odcięcia i następnie zbudowania na tej podstawie nowej dwuwartościowej zmiennej, przy której zostanie osiągnięty odpowiednio wysoki lub niski iloraz szans. Wykres dedykowany jest dla oceny zmiennych ciągłych w analizie jednoczynnikowej, tzn. gdy wybrana jest tylko jedna zmienna niezależna.
- Profile ilorazu szans - to wykres przedstawiający serie ilorazów szans wraz z przedziałem ufności, wyznaczane dla wskazanej wielkości okna tzn. porównujące częstości wewnątrz okna z częstościami umieszczonymi na zewnątrz okna. Umożliwia to użytkownikowi wybór kilku kategorii na jakie chce podzielić badaną zmienną i przyjęcie najkorzystniejszej kategorii referencyjnej. Najlepiej sprawdza się, gdy poszukujemy funkcji U-kształtnej tzn. o wysokim ryzyku przy niskich i przy wysokich wartościach badanej zmiennej, a o niskim przy wartościach przeciętnych. Nie ma jednej dobrej dla każdej analizy wielkości okna, wielkość tę należy ustalać indywidualnie dla każdej zmiennej. Wielkość okna wskazuje liczbę niepowtarzalnych wartości zmiennej X znajdujących się w oknie. Im szersze okno, tym większe uogólnienie wyników i gładsza funkcja ilorazu szans. Im węższe okno, tym bardziej szczegółowe wyniki, przez co bardziej rozchwiany iloraz szans. Do wykresu dodana jest krzywa ukazująca wygładzoną (metodą Lowess) wartość ilorazu szans. Ustawiając bliski 0 współczynnik wygładzania uzyskamy krzywą przylegającą ściśle do wyznaczonego ilorazu szans, natomiast ustawiając współczynnik wygładzania bliżej 1 dostaniemy większe uogólnienie ilorazu szans, a więc bardziej gładką i mniej przyległą do ilorazu szans krzywą. Wykres dedykowany jest dla oceny zmiennych ciągłych w analizie jednoczynnikowej, tzn. gdy wybrana jest tylko jedna zmienna niezależna.
Przykład (plik Profile OR.pqs)
Badamy ryzyko występowania choroby A i choroby B w zależności od BMI pacjenta. Ponieważ BMI jest zmienną ciągłą, to jej umieszczenie w modelu skutkuje wyznaczeniem jednostkowego ilorazu szans wyznaczającego liniowy trend wzrostu lub spadku ryzyka. Nie wiemy czy model liniowy będzie dobrym modelem dla analizy tego ryzyka, dlatego przed budowaniem wielowymiarowych modeli regresji logistycznej zbudujemy kilka modeli jednowymiarowych prezentujących tę zmienną na wykresach, by móc ocenić kształt badanej zależności i na tej podstawie zdecydować o sposobie w jaki powinniśmy przygotować zmienną do analizy. Do tego celu posłużą wykresy jednostkowych zmiany ilorazu szans i profili ilorazu szans, przy czym dla profili wybierzemy okno o wielkości 100, ponieważ prawie każdy pacjent ma inne BMI, więc około 100 pacjentów znajdzie się w każdym oknie.
- Choroba A
Jednostkowe zmiany ilorazu szans pokazują, że gdy punkt odcięcia BMI wybierzemy gdzieś między 27 a 37, to uzyskamy istotny statystycznie i dodatni iloraz szans pokazujący, że osoby mające BMI powyżej tej wartości mają istotnie wyższe ryzyko choroby niż osoby poniżej tej wartości.
Profile ilorazu szans pokazują, że czerwona krzywa znajduje się wciąż blisko jedynki, nieco wyżej jest tylko końcówka krzywej, co wskazuje że może być trudno podzielić BMI na więcej niż 2 kategorie i wybrać dobrą kategorię referencyjną, tzn. taką, która da istotne ilorazy szans.
Podsumowując, można skorzystać z podziału BMI na dwie wartości (np. odnieść osoby z BMI powyżej 30 do tych z BMI poniżej tej granicy, wówczas OR[95%CI]=[1.41, 4.90], p=0.0024) lub pozostać przy jednostkowym ilorazie szans, wskazującym stały wzrost ryzyka choroby przy wzroście BMI o jednostkę (OR[95%CI]=1.07[1.02, 1.13], p=0.0052).
- Choroba B
Jednostkowe zmiany ilorazu szans pokazują, że gdy punkt odcięcia BMI wybierzemy gdzieś między 22 a 35, to uzyskamy istotny statystycznie i dodatni iloraz szans pokazujący, że osoby mające BMI powyżej tej wartości mają istotnie wyższe ryzyko choroby niż osoby poniżej tej wartości.
Profile ilorazu szans pokazują, że znacznie lepiej byłoby podzielić BMI na 2 lub 4 kategorie. Przy czym kategorią referencyjną powinna być kategoria obejmująca BMI gdzieś pomiędzy 19 a 25, ponieważ to ta kategoria znajduje się najniżej i jest mocno oddalona od wyników dla BMI znajdujących się na lewo i na prawo od tego przedziału. Widzimy wyraźny kształt przypominający literę U, co oznacza, że ryzyko choroby jest wysokie przy niskim i przy wysokim BMI.
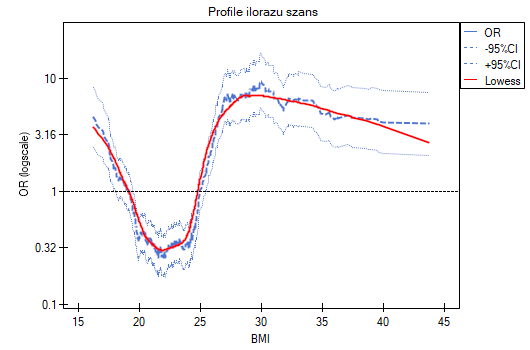
Podsumowując, mimo, że zależność dla jednostkowego ilorazu szans, czyli zależność liniowa jest istotna statystycznie, to nie warto budować takiego właśnie modelu. Znacznie lepiej podzielić BMI na kategorie. Podział pokazujący najlepiej kształt tej zależności, to podział wykorzystujący dwie lub trzy kategorie BMI, gdzie wartością odniesienia będzie przeciętne BMI. Wykorzystując standardowy podział BMI i ustanawiając kategorią odniesienia BMI w normie uzyskamy ponad 15 krotnie wyższe ryzyko dla osób z niedowagą (OR[95%CI]=15.14[6.93, 33.10]), ponad dziesięciokrotnie dla osób z nadwagą (OR[95%CI]=10.35[6.74, 15.90]) i ponad dwunastokrotnie dla osób z otyłością (OR[95%CI]=12.22[6.94, 21.49]).
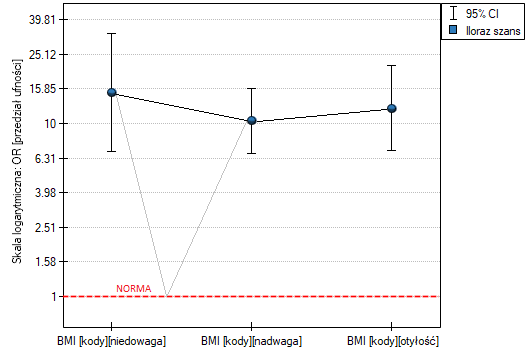
Na wykresie ilorazów szans norma BMI wskazana jest na poziomie 1, jako kategoria referencyjna. Dorysowaliśmy linie łączące uzyskane OR i również normę, tak by pokazać, że uzyskany kształt zależności jest tożsamy z wyznaczonym wcześniej poprzez profil ilorazu szans.
2021/01/11 22:02
Przykłady dla regresji logistycznej
Przeprowadzono badanie mające na celu identyfikację czynników ryzyka pewnej rzadko występującej wady wrodzonej u dzieci. W badaniu wzięło udział 395 matek dzieci z ta wadą oraz 375 matek dzieci zdrowych. Zebrane dane to: miejsce zamieszkania, płeć dziecka, masa urodzeniowa dziecka, wiek matki, kolejność ciąży, przebyte poronienia samoistne, infekcje oddechowe, palenie tytoniu, wykształcenie matki.
Budujemy model regresji logistycznej by sprawdzić które zmienne mogą wywierać istotny wpływ na występowanie wady. Jako zmienną zależną ustawiamy kolumnę GRUPA, wartością wyróżnioną w tej zmiennej jako  jest grupa
jest grupa badana, czyli matki dzieci z wadą wrodzoną. Kolejne  zmiennych, to zmienne niezależne:
zmiennych, to zmienne niezależne:
MiejsceZam (2=miasto/1=wieś),
Płeć (1=mężczyzna/0=kobieta),
MasaUr (w kilogramach z dokładnością do 0.5kg),
WiekM (w latach),
KolCiąży (dziecko z której ciąży),
PoronSamo (1=tak/0=nie),
InfOddech (1=tak/0=nie),
Palenie (1=tak/0=nie),
WyksztM (1=podstawowe lub niżej/2=zawodowe/3=średnie/4=wyższe).
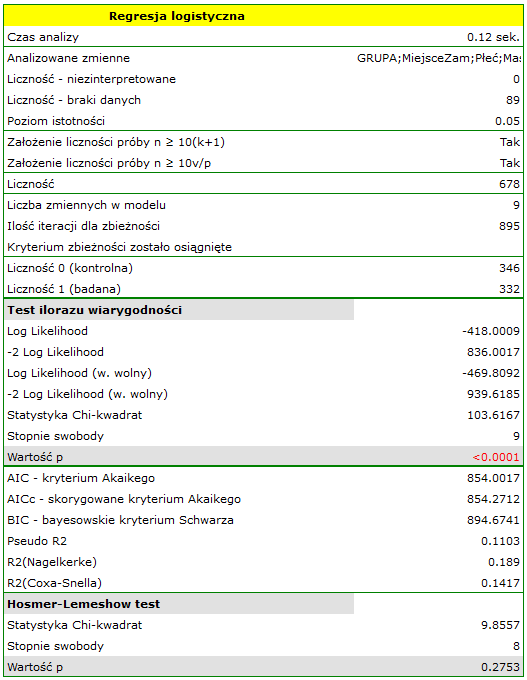
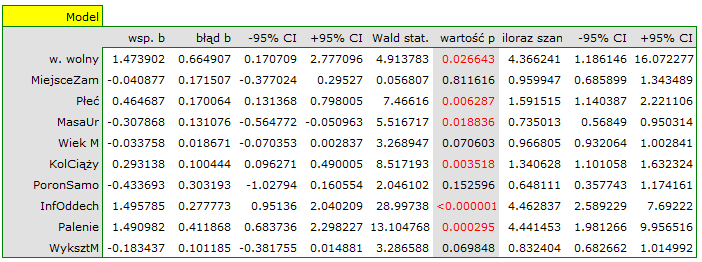
Jakość dopasowania modelu nie jest wysoka ( ,
,  i
i  ). Jednocześnie model jest istotny statystycznie (wartość
). Jednocześnie model jest istotny statystycznie (wartość 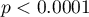 testu ilorazu wiarygodności), a zatem część zmiennych niezależnych znajdujących się w modelu jest istotna statystycznie. Wynik testu Hosmera-Lemeshowa wskazuje na brak istotności (
testu ilorazu wiarygodności), a zatem część zmiennych niezależnych znajdujących się w modelu jest istotna statystycznie. Wynik testu Hosmera-Lemeshowa wskazuje na brak istotności (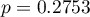 ). Przy czym, w przypadku testu Hosmera-Lemeshowa pamiętamy o tym, że brak istotności jest pożądany, bo wskazuje na podobieństwo liczności obserwowanych i prawdopodobieństwa przewidywanego.
). Przy czym, w przypadku testu Hosmera-Lemeshowa pamiętamy o tym, że brak istotności jest pożądany, bo wskazuje na podobieństwo liczności obserwowanych i prawdopodobieństwa przewidywanego.
Interpretacja poszczególnych zmiennych w modelu zaczyna się od sprawdzenia ich istotności. W tym przypadku zmienne, które w istotny sposób są związane z występowaniem wady to:
Płeć: 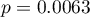 ,
,
MasaUr: 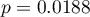 ,
,
KolCiąży: 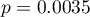 ,
,
InfOddech: 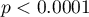 ,
,
Palenie: 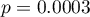 .
.
Badana wada wrodzona jest wadą rzadką, ale szansa na jej wystąpienie zależy od wymienionych zmiennych w sposób opisany poprzez iloraz szans:
- zmienna Płeć:
![LaTeX $OR[95\%CI]=1.60[1.14;2.22]$](/lib/exe/fetch.php?media=wiki:latex:/imgf8dc809d4d33fbf457e222bb2a246674.png) - szansa wystąpienia wady u chłopca jest
- szansa wystąpienia wady u chłopca jest 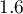 krotnie większa niż u dziewczynki;
krotnie większa niż u dziewczynki;
- zmienna MasaUr:
![LaTeX $OR[95\%CI]=0.74[0.57;0.95]$](/lib/exe/fetch.php?media=wiki:latex:/img5e023481fc641b1a88b75e8a1b4ba8be.png) - im wyższa masa urodzeniowa, tym szansa wystąpienia wady u dziecka jest mniejsza;
- im wyższa masa urodzeniowa, tym szansa wystąpienia wady u dziecka jest mniejsza;
- zmienna KolCiąży:
![LaTeX $OR[95\%CI]=1.34[1.10;1.63]$](/lib/exe/fetch.php?media=wiki:latex:/imgbc4c66db7606d854bbbbe9db1cbb0a16.png) - szansa wystąpienia wady u dziecka wzrasta wraz z każdą kolejną ciążą
- szansa wystąpienia wady u dziecka wzrasta wraz z każdą kolejną ciążą 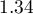 krotnie;
krotnie;
- zmienna InfOddech:
![LaTeX $OR[95\%CI]=4.46[2.59;7.69]$](/lib/exe/fetch.php?media=wiki:latex:/imga1c2b1a351fce6107ff7c7ccc044c83d.png) - szansa wystąpienia wady u dziecka, gdy matka w czasie ciąży przechodziła infekcje oddechową jest
- szansa wystąpienia wady u dziecka, gdy matka w czasie ciąży przechodziła infekcje oddechową jest 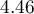 krotnie większa niż gdyby jej nie przechodziła;
krotnie większa niż gdyby jej nie przechodziła;
- zmienna Palenie:
![LaTeX $OR[95\%CI]=4.44[1.98;9.96]$](/lib/exe/fetch.php?media=wiki:latex:/img14fd8b0c97c85092641099b3a0c857d8.png) - matka paląca w czasie ciąży zwiększa
- matka paląca w czasie ciąży zwiększa 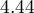 krotnie szansę na wystąpienia wady u dziecka
krotnie szansę na wystąpienia wady u dziecka
W przypadku zmiennych nieistotnych statystycznie przedział ufności dla Ilorazu Szans zawiera jedynkę co oznacza, że zmienne te nie zwiększają ani nie zmniejszają szansy na wystąpienie badanej wady. Nie można więc interpretować uzyskanego ilorazu w podobny sposób jak dla zmiennych istotnych statystycznie.
Wpływ poszczególnych zmiennych niezależnych na występowanie wady możemy równiez opisać przy pomocy wykresu dotyczącego ilorazu szans:
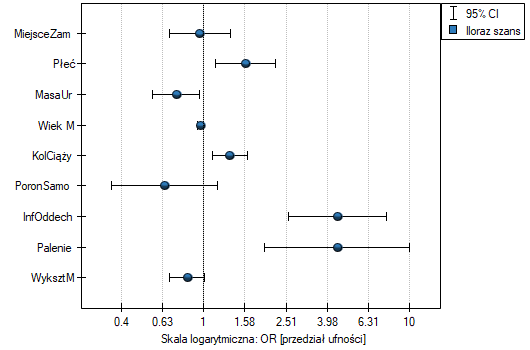
Przykład c.d. (wada.pqs)
Zbudujemy raz jeszcze model regresji logistycznej, ale tym razem zmienną wykształcenie rozbijemy na zmienne fikcyjne (kodowanie zero-jedynkowe). Tracimy tym samym informację o uporządkowaniu kategorii wykształcenia, ale zyskujemy możliwość wnikliwszej analizy poszczególnych kategorii. Rozbicia na zmienne fikcyjne dokonujemy wybierając w oknie analizy Zm. fikcyjne:
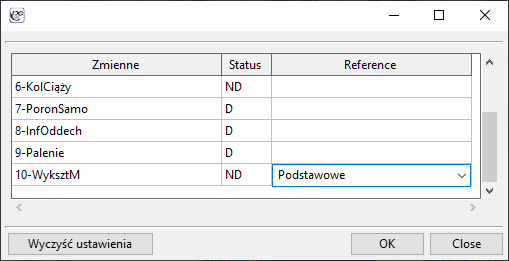
Wykształcenie podstawowe wybieramy jako kategorię odniesienia.
W rezultacie zmienne opisujące wykształcenie stają się istotne statystycznie. Dopasowanie modelu nie ulega znacznej zmianie, ale zmienia się sposób interpretacji ilorazu szans dla wykształcenia:
![LaTeX \begin{tabular}{|l|l|}
\hline
\textbf{Zmienna}& $OR[95\%CI]$ \\\hline
Wykształcenie podstawowe& kategoria referencyjna\\
Wykształcenie zawodowe& $0.51[0.26;0.99]$\\
Wykształcenie średnie& $0.42[0.22;0.80]$\\
Wykształcenie wyższe& $0.45[0.22;0.92]$\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img293c66232b211018957d259498fcf4db.png)
Szansa na wystąpienie badanej wady w każdej kategorii wykształcenia odnoszona jest zawsze do szansy wystąpienia wady przy wykształceniu podstawowym. Widzimy, że dla bardziej wykształconych matek, iloraz szans jest niższy. Dla matki z wykształceniem:
- zawodowym szansa wystąpienia wady u dziecka stanowi 0.51 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym;
- średnim szansa wystąpienia wady u dziecka stanowi 0.42 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym;
- wyższym szansa wystąpienia wady u dziecka stanowi 0.45 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym.
Przeprowadzono eksperyment mający na celu zbadanie umiejętność koncentracji grupy dorosłych podczas sytuacji niekomfortowych. W eksperymencie wzięło udział 190 osób (130 osób to zbiór uczący, 40 osób to zbiór testowy). Każda badana osoba dostała pewne zadanie, którego rozwiązanie wymagało skupienia uwagi. Podczas eksperymentu niektóre osoby zostały poddane działaniu czynnika zakłócającego jakim była podwyższona temperatura powietrza do 32 stopni Celsiusza. Osoby biorące udział w eksperymencie zapytano dodatkowo o ich miejsce zamieszkania, płeć, wiek i wykształcenie. Czas na rozwiązanie zadania ograniczono do 45 minut. Dla osób, które skończyły przed czasem odnotowano rzeczywisty czas poświęcony na rozwiązanie. Całość naszych obliczeń wykonamy tylko dla osóbnależących do zbioru uczącego.
Zmienna ROZWIĄZANIE (tak/nie) zawiera wynik eksperymentu, czyli informację o tym, czy zadanie zostało rozwiązane poprawnie czy też nie. Pozostałe zmienne, które mogły wpływać na wynik eksperymentu to:
MIEJSCEZAM (1=miasto/0=wieś),
PŁEĆ (1=kobieta/0=mężczyzna),
WIEK (w latach),
WYKSZTAŁCENIE (1=podstawowe, 2=zawodowe, 3=średnie, 4=wyższe),
CZAS rozwiązywania (w minutach),
ZAKŁÓCENIA (1=tak/0=nie).
Na bazie wszystkich zmiennych zbudowano model regresji logistycznej, gdzie jako stan wyróżniony zmiennej ROZWIĄZANIE wybrano tak.
Jakość jego dopasowania opisują współczynniki: 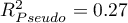 ,
, 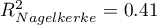 i
i 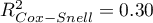 . Na wystarczającą jakość dopasowania wskazuje również wynik testu Hosmera-Lemeshowa
. Na wystarczającą jakość dopasowania wskazuje również wynik testu Hosmera-Lemeshowa 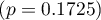 . Cały model jest istotny statystycznie o czym mówi wynik testu ilorazu wiarygodności
. Cały model jest istotny statystycznie o czym mówi wynik testu ilorazu wiarygodności 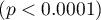 .
.
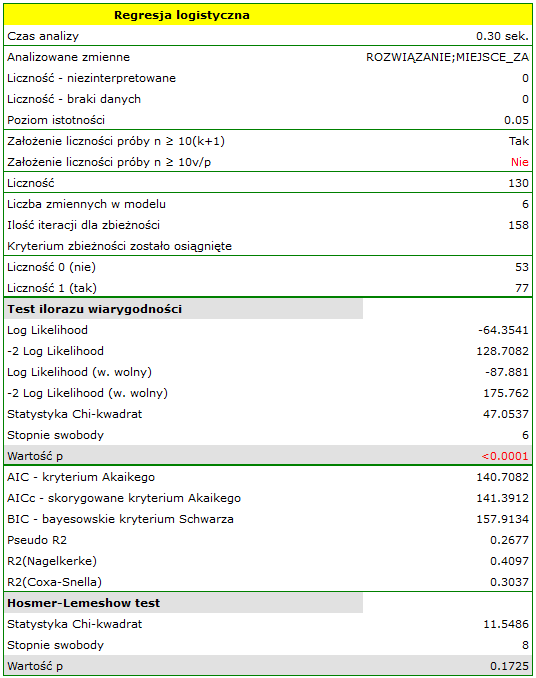
Wartości obserwowane i prawdopodobieństwo przewidywane możemy zobaczyć na wykresie:

W modelu zmienne, które w sposób istotny wpływają na wynik to:
WIEK: 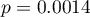 ,
,
CZAS: 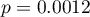 ,
,
ZAKŁÓCENIA: 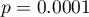 .
.
Przy czym, im osoba rozwiązująca jest młodsza, czas rozwiązywania krótszy i brak jest czynnika zakłócającego, tym większe prawdopodobieństwo poprawnego rozwiązania:
WIEK: ![LaTeX $OR[95\%CI]=0.90[0.85;0.96]$](/lib/exe/fetch.php?media=wiki:latex:/img2d561911e46044388c920f350283e92f.png) ,
,
CZAS: ![LaTeX $OR[95\%CI]=0.91[0.87;0.97]$](/lib/exe/fetch.php?media=wiki:latex:/img856be89e1314daa3623408b907f11c45.png) ,
,
ZAKŁÓCENIA: ![LaTeX $OR[95\%CI]=0.15[0.06;0.37]$](/lib/exe/fetch.php?media=wiki:latex:/img8cb35d4670d9bda19bc8f3dd46b985b3.png) .
.
Uzyskane wyniki Ilorazu Szans przedstawiono na poniższym wykresie:

Jeśli model miałby zostać użyty do prognozowania, to należy przyjrzeć się jakości klasyfikacji. Wyliczamy w tym celu krzywe ROC.
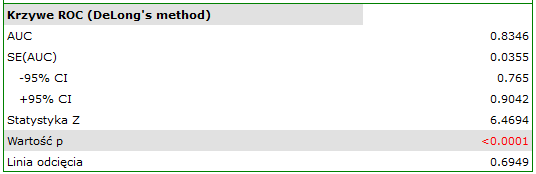

Rezultat wydaje się zadowalający. Pole pod krzywą wynosi 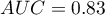 i jest istotnie większe niż
i jest istotnie większe niż 
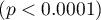 , więc na podstawie zbudowanego modelu można klasyfikować. Proponowany punkt odcięcia dla krzywej ROC wynosi
, więc na podstawie zbudowanego modelu można klasyfikować. Proponowany punkt odcięcia dla krzywej ROC wynosi 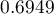 i jest nieco wyższy niż standardowo używany w regresji poziom
i jest nieco wyższy niż standardowo używany w regresji poziom 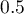 . Klasyfikacja wyznaczona na bazie tego punktu odcięcia daje 79,23% przypadków zaklasyfikowanych poprawnie, z czego poprawnie zaklasyfikowanych wartości „tak” jest 72.73% (czułość), wartości „nie” jest 88.68% (swoistość). Klasyfikacja uzyskana na podstawie standardowej wartości daje nie co mniej, bo 73.85% przypadków zaklasyfikowanych poprawnie, ale uzyskamy dzięki niej więcej poprawnie zaklasyfikowanych wartości „tak” jest 83.12%, choć mniej poprawnie zaklasyfikowanych wartości „nie” jest 60.38%.
. Klasyfikacja wyznaczona na bazie tego punktu odcięcia daje 79,23% przypadków zaklasyfikowanych poprawnie, z czego poprawnie zaklasyfikowanych wartości „tak” jest 72.73% (czułość), wartości „nie” jest 88.68% (swoistość). Klasyfikacja uzyskana na podstawie standardowej wartości daje nie co mniej, bo 73.85% przypadków zaklasyfikowanych poprawnie, ale uzyskamy dzięki niej więcej poprawnie zaklasyfikowanych wartości „tak” jest 83.12%, choć mniej poprawnie zaklasyfikowanych wartości „nie” jest 60.38%.
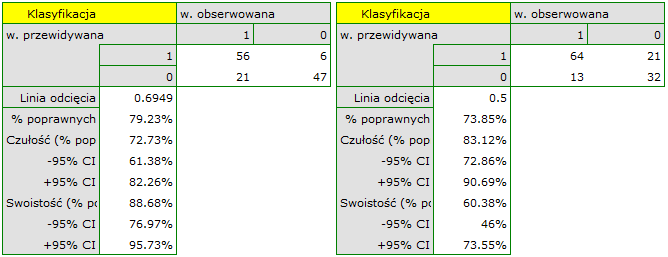
Na tym etapie możemy zakończyć analizę klasyfikacji, lub jeśli wynik nie jest wystarczający bardziej wnikliwą analizę krzywej ROC możemy przeprowadzić w module Krzywa ROC.
Ponieważ uznaliśmy, że klasyfikacja na podstawie modelu jest zadowalająca, możemy wyliczyć prognozowaną wartość zmiennej zależnej dla dowolnie zadanych warunków. Sprawdźmy jakie szanse na rozwiązanie zadania ma osoba dla której:
MIEJSCEZAM (1=miasto),
PŁEĆ (1=kobieta),
WIEK (50 lat),
WYKSZTAŁCENIE (1=podstawowe),
CZAS rozwiązywania (20 minut),
ZAKŁÓCENIA (1=tak).
W tym celu na podstawie wartości współczynnika  wyliczane jest prawdopodobieństwo przewidywane (prawdopodobieństwo uzyskania odpowiedzi
wyliczane jest prawdopodobieństwo przewidywane (prawdopodobieństwo uzyskania odpowiedzi tak pod warunkiem określenia wartości zmiennych zależnych):
![LaTeX \begin{displaymath}
\begin{array}{l}
P(Y=tak|MIEJSCEZAM,PŁEĆ,WIEK,WYKSZTAŁCENIE,CZAS,ZAKŁÓCENIA)=\\[0.2cm]
=\frac{e^{7.23-0.45\textrm{\scriptsize \textit{MIEJSCEZAM}}-0.45\textrm{\scriptsize\textit{PŁEĆ}}-0.1\textrm{\scriptsize\textit{WIEK}}+0.46\textrm{\scriptsize\textit{WYKSZTAŁCENIE}}-0.09\textrm{\scriptsize\textit{CZAS}}-1.92\textrm{\scriptsize\textit{ZAKŁÓCENIA}}}}{1+e^{7.23-0.45\textrm{\scriptsize\textit{MIEJSCEZAM}}-0.45\textrm{\scriptsize\textit{PŁEĆ}}-0.1\textrm{\scriptsize\textit{WIEK}}+0.46\textrm{\scriptsize\textit{WYKSZTAŁCENIE}}-0.09\textrm{\scriptsize\textit{CZAS}}-1.92\textrm{\scriptsize\textit{ZAKŁÓCENIA}}}}=\\[0.2cm]
=\frac{e^{7.231-0.453\cdot1-0.455\cdot1-0.101\cdot50+0.456\cdot1-0.089\cdot20-1.924\cdot1}}{1+e^{7.231-0.453\cdot1-0.455\cdot1-0.101\cdot50+0.456\cdot1-0.089\cdot20-1.924\cdot1}}
\end{array}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img05c978955ec4691a8e7bfe3d265dc858.png)
W rezultacie tych obliczeń program zwróci wynik:
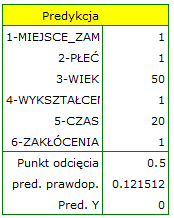
Uzyskane prawdopodobieństwo rozwiązania zadania wynosi 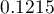 , więc na podstawie punktu odcięcia
, więc na podstawie punktu odcięcia 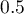 przewidziany wynik to
przewidziany wynik to  - czyli zadanie nie rozwiązane poprawnie.
- czyli zadanie nie rozwiązane poprawnie.
2021/01/11 22:02
Predykcja na podstawie modelu i walidacja zbioru testowego
Walidacja
Walidacja modelu to sprawdzenie jego jakości. W pierwszej kolejności wykonywana jest na danych, na których model był zbudowany (zbiór uczący), czyli zwracana jest w raporcie opisującym uzyskany model. By można było z większą pewnością osądzić na ile model nadaje się do prognozy nowych danych, ważnym elementem walidacji jest zastosowaniee modelu do danych, które nie były wykorzystywane w estymacji modelu. Jeśli podsumowanie w oparciu o dane uczące będzie satysfakcjonujące tzn. wyznaczane błędy, współczynniki  i kryteria informacyjne będą na zadowalającym nas poziomie, a podsumowanie w oparciu o nowe dane (tzw. zbiór testowy) będzie równie korzystne, wówczas z dużym prawdopodobieństwem można uznać, że taki model nadaje się do predykcji. Dane testujące powinny pochodzić z tej samej populacji, z której były wybrane dane uczące. Często jest tak, że przed przystąpieniem do budowy modelu zbieramy dane, a następnie w sposób losowy dzielimy je na zbiór uczący, czyli dane które posłużą do budowy modelu i zbiór testowy, czyli dane które posłużą do dodatkowej walidacji modelu.
i kryteria informacyjne będą na zadowalającym nas poziomie, a podsumowanie w oparciu o nowe dane (tzw. zbiór testowy) będzie równie korzystne, wówczas z dużym prawdopodobieństwem można uznać, że taki model nadaje się do predykcji. Dane testujące powinny pochodzić z tej samej populacji, z której były wybrane dane uczące. Często jest tak, że przed przystąpieniem do budowy modelu zbieramy dane, a następnie w sposób losowy dzielimy je na zbiór uczący, czyli dane które posłużą do budowy modelu i zbiór testowy, czyli dane które posłużą do dodatkowej walidacji modelu.
Okno z ustawieniami opcji walidacji wywołujemy poprzez menu Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna - predykcja/walidacja.
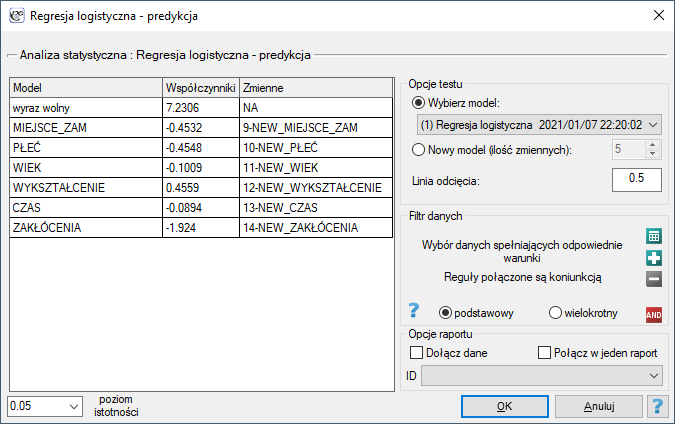
By dokonać walidacji należy wskazać model, na podstawie którego chcemy jej dokonać. Walidacji możemy dokonać na bazie:
- zbudowanego w PQStat modelu regresji logistycznej - wystarczy wybrać model spośród modeli przypisanych do danego arkusza, a liczba zmiennych i współczynniki modelu zostaną ustawione automatycznie; zbiór testowy powinien się znaleźć w tym samym arkuszu co zbiór uczący;
- modelu nie zbudowanego w programie PQStat, ale uzyskanego z innego źródła (np. opisanego w przeczytanej przez nas pracy naukowej) - w oknie analizy należy podać liczbę zmiennych oraz wpisać współczynniki dotyczące każdej z nich.
W oknie analizy należy wskazać te nowe zmienne, które powinny zostać wykorzystane do walidacji.
Predykcja
Najczęściej ostatnim etapem analizy regresji jest wykorzystanie zbudowanego i uprzednio zweryfikowanego modelu do predykcji.
- Predykcja dla jednego obiektu może być wykonywana wraz z budową modelu, czyli w oknie analizy
Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna, - Predykcja dla większej grupy nowych danych jest wykonywana poprzez menu
Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna - predykcja/walidacja.
By dokonać predykcji należy wskazać model, na podstawie którego chcemy jej dokonać. Predykcji możemy dokonać na bazie:
- zbudowanego w PQStat modelu regresji logistycznej - wystarczy wybrać model spośród modeli przypisanych do danego arkusza, a liczba zmiennych i współczynniki modelu zostaną ustawione automatycznie; zbiór testowy powinien się znaleźć w tym samym arkuszu co zbiór uczący;
- modelu nie zbudowanego w programie PQStat, ale uzyskanego z innego źródła (np. opisanego w przeczytanej przez nas pracy naukowej) - w oknie analizy należy podać liczbę zmiennych oraz wpisać współczynniki dotyczące każdej z nich.
W oknie analizy należy wskazać te nowe zmienne, które powinny zostać wykorzystane do predykcji.
Na podstawie nowych danych wyznaczana jest wartość prawdopodobieństwa przewidywanego przez model a następnie predykacja wystąpienia zdarzenia (1) lub jego braku (0). Punkt odcięcia, na podstawie którego wykonywana jest klasyfikacja to domyślnie wartość 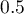 . Użytkownik może zmienić tę wartość na dowolną wartość z przedziału
. Użytkownik może zmienić tę wartość na dowolną wartość z przedziału  np. wartość sugerowaną przez krzywą ROC.
np. wartość sugerowaną przez krzywą ROC.
Przykład c.d. (plik zadanie.pqs)
W eksperymencie badającym umiejętność koncentracji, dla grupy 130 osób zbioru uczącego, zbudowano model regresji logistycznej w oparciu o następujące zmienne:
zmienna zależna: ROZWIĄZANIE (tak/nie) - informacja o tym, czy zadanie zostało rozwiązane poprawnie czy też nie;
zmienne niezależne:
MIEJSCEZAM (1=miasto/0=wieś),
PŁEĆ (1=kobieta/0=mężczyzna),
WIEK (w latach),
WYKSZTAŁCENIE (1=podstawowe, 2=zawodowe, 3=średnie, 4=wyższe),
CZAS rozwiązywania (w minutach),
ZAKŁÓCENIA (1=tak/0=nie).
Jednak tylko cztery zmienne: WIEK, WYKSZTAŁCENIE, CZAS rozwiązywania i ZAKŁÓCENIA, wnoszą istotne informacje do modelu. Zbudujemy model dla danych zbioru uczącego w oparciu o te cztery zmienne a następnie, by się upewnić że będzie działał poprawnie, zwalidujemy go na testowym zbierze danych. Jeśli model przejdzie tę próbę, to będziemy go stosować do predykcji dla nowych osób. By korzystać z odpowiednich zbiorów ustawiamy każdorazowo filtr danych.
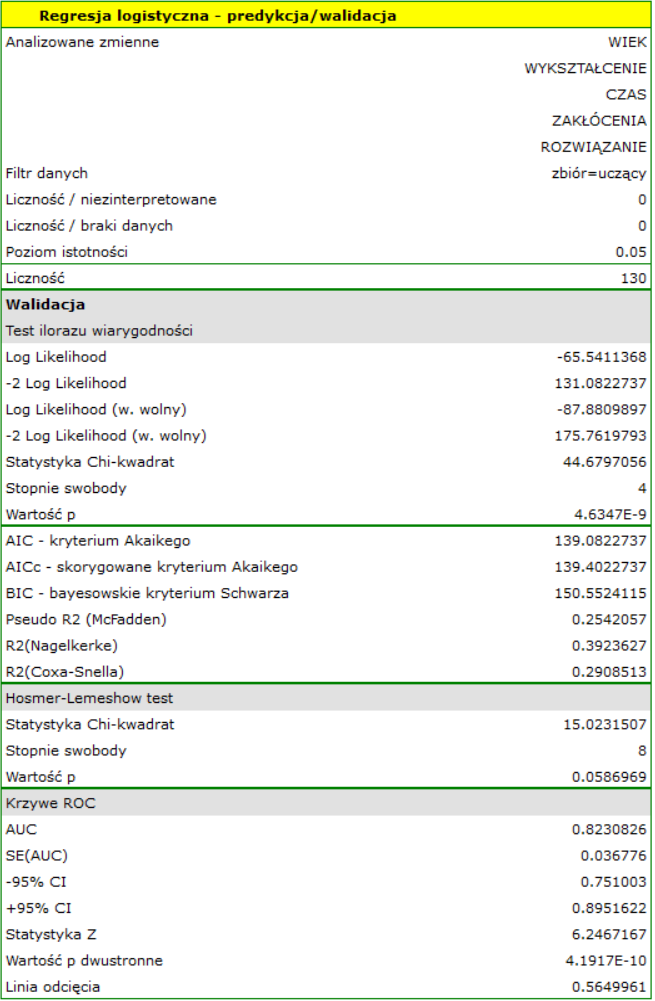
Dla zbioru uczącego wartości opisujące jakość dopasowania modelu nie są bardzo wysokie 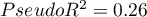 a
a 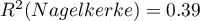 , ale już jakość jego predykcji jest zadowalająca (AUC[95%CI]=0.82[0.75, 0.90], czułość =82%, swoistość 60%).
, ale już jakość jego predykcji jest zadowalająca (AUC[95%CI]=0.82[0.75, 0.90], czułość =82%, swoistość 60%).
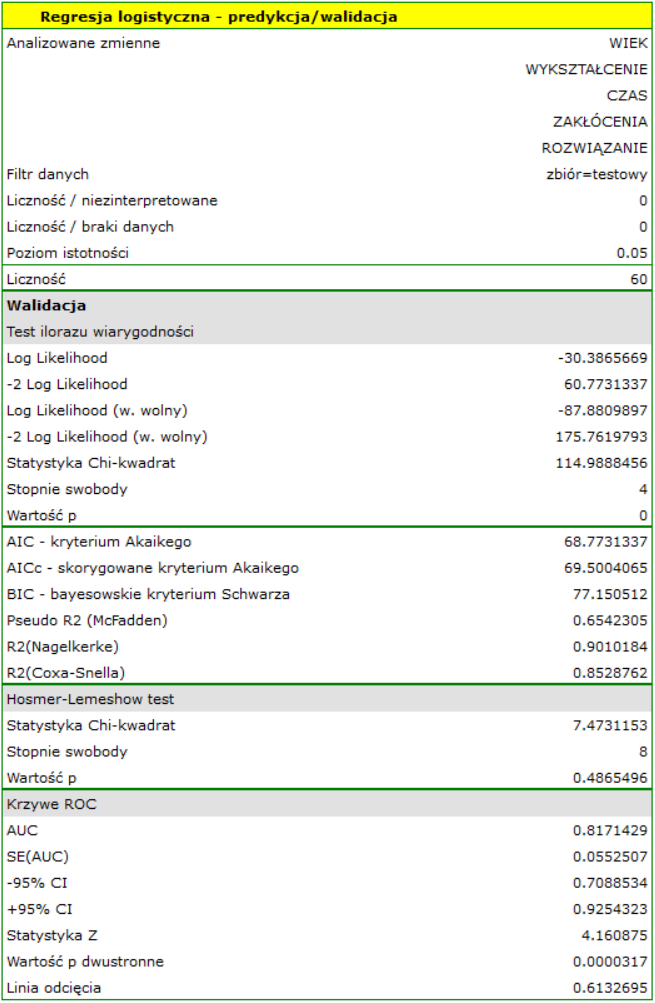
Dla zbioru testowego wartości opisujące jakość dopasowania modelu są nawet wyższe niż dla danych uczących 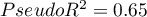 a
a 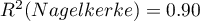 . Jakość predykcji dla danych testowych jest wciąż zadowalająca (AUC[95%CI]=0.82[0.71, 0.93], czułość =73%, swoistość 64%), dlatego użyjemy modelu do predykcji. W tym celu skorzystamy z danych trzech nowych osób dopisanych na końcu zbioru. Wybierzemy opcję
. Jakość predykcji dla danych testowych jest wciąż zadowalająca (AUC[95%CI]=0.82[0.71, 0.93], czułość =73%, swoistość 64%), dlatego użyjemy modelu do predykcji. W tym celu skorzystamy z danych trzech nowych osób dopisanych na końcu zbioru. Wybierzemy opcję Predykcja, ustawimy filtr na nowy zbiór danych i użyjemy naszego modelu do tego by przewidzieć czy dana osoba rozwiąże zadanie poprawnie (uzyska wartość 1) czy też niepoprawnie (uzyska wartość 0).
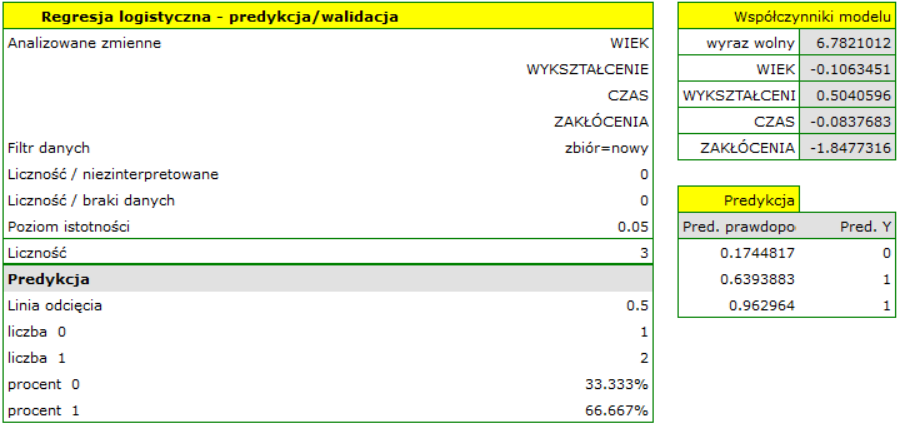
Okazuję się, że prognoza dla pierwszej osoby jest negatywna, a dla dwóch kolejnych pozytywna. Prognoza dla 50-letniej kobiety z wykształceniem podstawowym rozwiązującej test podczas zakłóceń w czasie 20 min wynosi 0.17, co oznacza że prognozujemy iż rozwiąze ona zadanie niepoprawnie, podczas gdy pronoza dla kobiety o 20 lat młodszej jest już korzystna - prawdopodobieństwo rozwiązania przez nią zadania wynosi 0.64. Największe prawdopodobieństwo (równe 0.96) poprawnego rozwiazania ma trzecia kobieta, która rozwiązywała test w ciągu 10 minut i bez zakłuceń.
Gdybyśmy chcieli postawić prognozę na podstawie innego modelu (np. uzyskanego podczas innego badania naukowego: ROZWIĄZANIE=6-0.1*WIEK+0.5*WYKSZT-0.1*CZAS-2*ZAKŁÓCENIA) - wystrczy, że w oknie analizy wybierzemy nowy model, ustawimy jego współczynniki i porgnozę dla wybraych osób można powtórzyć w oparciu o ten model.
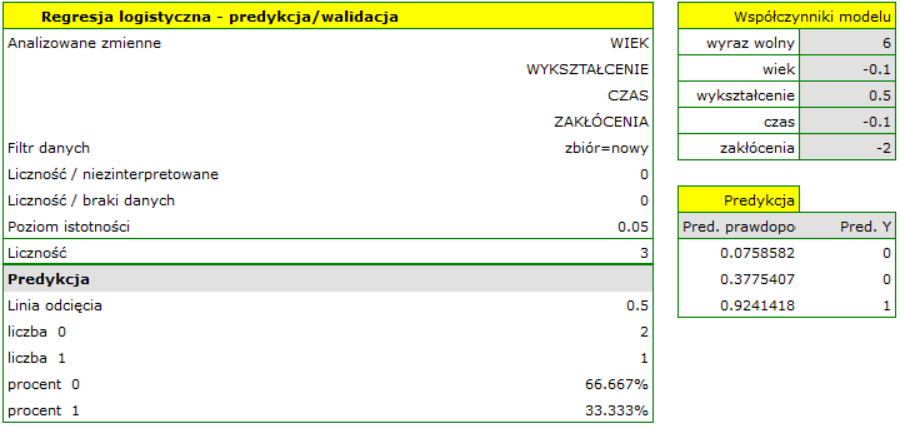
Tym razem, zgodnie z prognozą nowego modelu, przewidywania dla pierwszej i drugiej osoby są negatywne, a trzeciej pozytywne.
2021/01/11 22:02
2014/08/22 20:00
Porównywanie modeli regresji logistycznej
Okno z ustawieniami opcji porównywania modeli wywołujemy poprzez menu Statystyka zaawansowana→Modele wielowymiarowe→Regresja logistyczna - porównywanie modeli
 Ze względu na możliwość jednoczesnej analizy wielu zmiennych niezależnych w jednym modelu regresji logistycznej, podobnie jak w liniowej regresji wielorakiej, istnieje problem wyboru optymalnego modelu. Wybierając zmienne niezależne należy pamiętać, by w modelu znajdowały się zmienne silnie skorelowane ze zmienną zależną i słabo skorelowane między sobą.
Ze względu na możliwość jednoczesnej analizy wielu zmiennych niezależnych w jednym modelu regresji logistycznej, podobnie jak w liniowej regresji wielorakiej, istnieje problem wyboru optymalnego modelu. Wybierając zmienne niezależne należy pamiętać, by w modelu znajdowały się zmienne silnie skorelowane ze zmienną zależną i słabo skorelowane między sobą.
Porównując modele z różną liczbą zmiennych niezależnych zwracamy uwagę na dopasowanie modelu oraz kryteria informacyjne. Dla każdego modelu wyliczamy również maksimum funkcji wiarygodności, które następnie porównujemy przy użyciu testu ilorazu wiarygodności.
Hipotezy:
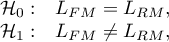
gdzie:
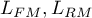 - maksimum funkcji wiarygodności w porównywanych modelach (pełnym i zredukowanym).
- maksimum funkcji wiarygodności w porównywanych modelach (pełnym i zredukowanym).
Statystyka testowa ma postać:
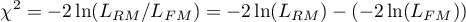
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 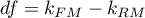 stopniami swobody, gdzie
stopniami swobody, gdzie 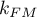 i
i 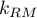 to ilość szacowanych parametrów w porównywanych modelach.
to ilość szacowanych parametrów w porównywanych modelach.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Decyzję o tym, który model wybrać podejmujemy na podstawie wielkości 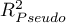 ,
, 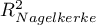 ,
, 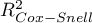 oraz wyniku testu ilorazu wiarygodności porównującego kolejno powstające (sąsiednie) modele. Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne, które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym
oraz wyniku testu ilorazu wiarygodności porównującego kolejno powstające (sąsiednie) modele. Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne, które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym  i mniejszej wartości kryterium informacyjnego AIC, AICc lub BIC) jest istotnie lepszy niż drugi.
i mniejszej wartości kryterium informacyjnego AIC, AICc lub BIC) jest istotnie lepszy niż drugi.
Porównanie wartości prognostycznej modeli.
Budowane modele regresji pozwalają przewidzieć prawdopodobieństwo wystąpienia badanego zdarzenia w oparciu o analizowane zmienne niezależne. Gdy znanych jest już wiele zmiennych (czynników) zwiększających ryzyko wystąpienia zdarzenia, wówczas ważnym kryterium dla nowego kandydata na czynnik ryzyka jest poprawa skuteczności predykcji po dołączeniu tego czynnika do modelu.
Dla ustalenia uwagi posłużmy się przykładem. Załóżmy, że badamy czynniki ryzyka wystąpienia choroby wieńcowej. Do znanych czynników ryzyka tej choroby należą wiek, wartości ciśnienia skurczowego i rozkurczowego, otyłość, cholesterol czy też palenie. Badacze są jednak zainteresowani jak bardzo włączenie poszczególnych czynników do modelu regresji pozwoli na znaczną poprawę oszacowywania ryzyka wystąpienia choroby. Czynniki ryzyka dołączone do modelu będą miały znaczenie prognostyczne, jeśli nowy i większy model (zawierający te czynniki) będzie wykazywał lepszą wartość prognostyczną niż model ich pozbawiony.
Wartość prognostyczna modelu wynika z wyznaczonej wartości przewidywanego prawdopodobieństwa wystąpienia zdarzenia, w tym przypadku choroby wieńcowej. Wartość ta jest wyznaczana na podstawie modelu dla każdej badanej osoby. Im bliższe wartości 1 jest przewidywane prawdopodobieństwo, tym bardziej prawdopodobna jest choroba. Na bazie prawdopodobieństwa przewidywanego można wyznaczyć i porównać pomiędzy różnymi modelami wartość pola AUC pod krzywą ROC a także współczynnik  i
i  .
.
- Zmiana pola pod krzywą ROC
Krzywa ROC w modelach regresji logistycznej zbudowana jest w oparciu o klasyfikację przypadków do grupy doświadczającej zdarzenia lub nie, oraz przewidywane prawdopodobieństwo zmiennej zależnej  . Czym większe pole pod krzywą, tym trafniej prawdopodobieństwo wyznaczone przez model przewiduje rzeczywiste wystąpienie zdarzenia. Jeśli porównujemy modele zbudowane w oparciu o większą lub mniejszą liczbę czynników prognostycznych, to porównując wielkość pola pod krzywą możemy sprawdzić, czy dołożenie czynników poprawiło znacząco predykcję modelu.
. Czym większe pole pod krzywą, tym trafniej prawdopodobieństwo wyznaczone przez model przewiduje rzeczywiste wystąpienie zdarzenia. Jeśli porównujemy modele zbudowane w oparciu o większą lub mniejszą liczbę czynników prognostycznych, to porównując wielkość pola pod krzywą możemy sprawdzić, czy dołożenie czynników poprawiło znacząco predykcję modelu.
Hipotezy:
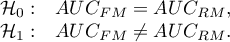
Sposób wyznaczania staystyki testowej oparty o metodę DeLonga, został opisany w rozdziale Porównywanie krzywych ROC.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Poprawa reklasyfikacji netto
Miara ta oznaczana jest skrótem  (ang. Net Reclassification Improvement).
(ang. Net Reclassification Improvement).  skupia się na tabeli reklasyfikacji opisującej przesunięcie wartości prawdopodobieństwa w górę lub w dół po dołożeniu nowego czynnika do modelu. Wyznacza się go na bazie dwóch oddzielnych współczynników, tzn. współczynnika wyznaczonego oddzielnie dla obiektów doświadczających zdarzenia (1) i oddzielnie dla tych niedoświadczających zdarzenia (0).
skupia się na tabeli reklasyfikacji opisującej przesunięcie wartości prawdopodobieństwa w górę lub w dół po dołożeniu nowego czynnika do modelu. Wyznacza się go na bazie dwóch oddzielnych współczynników, tzn. współczynnika wyznaczonego oddzielnie dla obiektów doświadczających zdarzenia (1) i oddzielnie dla tych niedoświadczających zdarzenia (0).  może być wyznaczany przy zadanym podziale prawdopodobieństwa przewidywanego na kategorie (
może być wyznaczany przy zadanym podziale prawdopodobieństwa przewidywanego na kategorie ( kategorialny) lub bez konieczności wyznaczania kategorii (
kategorialny) lub bez konieczności wyznaczania kategorii ( ciągły).
ciągły).
- NRI kategorialny wymaga arbitralnego wyznaczenia podziału wartości prawdopodobieństwa przewidywanego z modelu. Podanych punktów podziału może być maksymalnie 9, a więc przewidywanych kategorii maksymalnie 10. Najczęściej jednak stosuje się jeden lub dwa punkty podziałowe. Przy czym należy zauważyć, że wartości kategorialnego
 mogą być z sobą porównywane tylko wtedy, jeśli bazowały na tych samych punktach podziału. Dla zobrazowania sytuacji ustalmy dwa przykładowe punkty podziału prawdopodobieństwa: 0.1 i 0.3. Jeśli badana osoba w modelu „starym” (mniejszym) uzyskała prawdopodobieństwo poniżej 0.1, a w „nowym modelu” (zwiększonym o nowy potencjalny czynnik ryzyka) prawdopodobieństwo znajdujące się pomiędzy 0.1 a 0.3, to znaczy, że osoba ta została reklasyfikowana w górę (tabela, sytuacja 1). Jeśli wartość prawdopodobieństwa z obu modeli mieści się w tym samym przedziale, wówczas osoba nie została reklasyfikowana (tabela, sytuacja 2), natomiast jeśli prawdopodobieństwo z modelu „nowego” będzie niższe niż w modelu „starym”, oznacza to reklasyfikację w dół badanej osoby (tabela, sytuacja 3).
mogą być z sobą porównywane tylko wtedy, jeśli bazowały na tych samych punktach podziału. Dla zobrazowania sytuacji ustalmy dwa przykładowe punkty podziału prawdopodobieństwa: 0.1 i 0.3. Jeśli badana osoba w modelu „starym” (mniejszym) uzyskała prawdopodobieństwo poniżej 0.1, a w „nowym modelu” (zwiększonym o nowy potencjalny czynnik ryzyka) prawdopodobieństwo znajdujące się pomiędzy 0.1 a 0.3, to znaczy, że osoba ta została reklasyfikowana w górę (tabela, sytuacja 1). Jeśli wartość prawdopodobieństwa z obu modeli mieści się w tym samym przedziale, wówczas osoba nie została reklasyfikowana (tabela, sytuacja 2), natomiast jeśli prawdopodobieństwo z modelu „nowego” będzie niższe niż w modelu „starym”, oznacza to reklasyfikację w dół badanej osoby (tabela, sytuacja 3).
![LaTeX \begin{tabular}{|c|c|c||c|c||c|c|}
\hline
modele regresji&\multicolumn{2}{|c||}{sytuacja 1}&\multicolumn{2}{|c||}{sytuacja 2}&\multicolumn{2}{|c|}{sytuacja 3}\\\hline
prawdop. przewidywane&"stary"&"nowy"&"stary"&"nowy"&"stary"&"nowy"\\\hline
[0.3 do 1]&&&&&$\oplus$&\\\hline
[0.1; 0.3)&&$\oplus$&$\oplus$&$\oplus$&&$\oplus$\\\hline
[0; 0.1)&$\oplus$&&&&&\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img2625dcf065b9f89d09a26cab3972ac0f.png)
- NRI ciągły nie wymaga arbitralnego wyznaczenia kategorii, ponieważ każda, nawet najmniejsza zmiana prawdopodobieństwa w górę lub w dół w stosunku do prawdopodobieństwa wyznaczonego w „starym modelu”, traktowana jest jako przejście do kolejnej kategorii. Kategorii jest więc nieskończenie wiele, tak jak wiele jest możliwych zmian.
Uwaga!
Stosowanie  ciągłego nie wymaga arbitralnego definiowania punktów podziału prawdopodobieństwa, jednak nawet niewielkie zmiany ryzyka (nie mające odzwierciedlenia w klinicznych obserwacjach) mogą wpływać na zwiększenie lub zmniejszenie tego współczynnika. Kategorialny współczynnik
ciągłego nie wymaga arbitralnego definiowania punktów podziału prawdopodobieństwa, jednak nawet niewielkie zmiany ryzyka (nie mające odzwierciedlenia w klinicznych obserwacjach) mogą wpływać na zwiększenie lub zmniejszenie tego współczynnika. Kategorialny współczynnik  pozwala na odzwierciedlenie tylko ważnych dla badacza zmian polegających na przekroczeniu zadanych wartości ryzyka wystąpienia zdarzenia (wartości prawdopodobieństwa przewidywanego).
pozwala na odzwierciedlenie tylko ważnych dla badacza zmian polegających na przekroczeniu zadanych wartości ryzyka wystąpienia zdarzenia (wartości prawdopodobieństwa przewidywanego).
By wyznaczyć  definiujemy:
definiujemy:
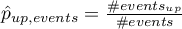
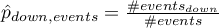
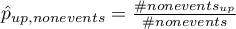
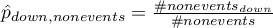
gdzie:
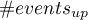 - liczba obiektów z grupy doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w górę,
- liczba obiektów z grupy doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w górę,
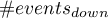 - liczba obiektów z grupy doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w dół,
- liczba obiektów z grupy doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w dół,
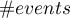 - liczba obiektów w grupie doświadczającej zdarzenia,
- liczba obiektów w grupie doświadczającej zdarzenia,
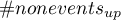 - liczba obiektów z grupy nie doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w górę,
- liczba obiektów z grupy nie doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w górę,
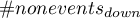 - liczba obiektów z grupy nie doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w dół,
- liczba obiektów z grupy nie doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w dół,
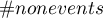 - liczba obiektów w grupie nie doświadczającej zdarzenia.
- liczba obiektów w grupie nie doświadczającej zdarzenia.
Ogólny współczynnik  oraz współczynniki wyrażające procentową zmianę klasyfikacji jest wyznaczany z wzoru:
oraz współczynniki wyrażające procentową zmianę klasyfikacji jest wyznaczany z wzoru:
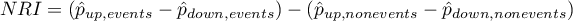
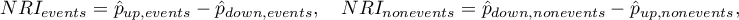
Współczynnik 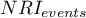 może być interpretowany jako procent netto prawidłowo reklasyfikowanych osób, u których wystąpiło zdarzenie, a
może być interpretowany jako procent netto prawidłowo reklasyfikowanych osób, u których wystąpiło zdarzenie, a 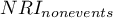 jako procent netto prawidłowo reklasyfikowanych osób, u których nie wystąpiło zdarzenie. Ogólny współczynnik
jako procent netto prawidłowo reklasyfikowanych osób, u których nie wystąpiło zdarzenie. Ogólny współczynnik  jest wyrażony jako suma współczynników
jest wyrażony jako suma współczynników 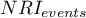 i
i 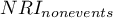 , przez co jest współczynnikiem domyślnie ważonym przez częstość zdarzenia i nie może być interpretowany jako procent.
, przez co jest współczynnikiem domyślnie ważonym przez częstość zdarzenia i nie może być interpretowany jako procent.
Współczynniki 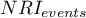 należą do przedziału od -1 do 1 (od -100% do 100%), a ogólny współczynniki
należą do przedziału od -1 do 1 (od -100% do 100%), a ogólny współczynniki  do przedziału od -2 do 2. Wartości dodatnie współczynników świadczą o korzystnej reklasyfikacji, a ujemne o niekorzystnej reklasyfikacji na skutek dołożenia nowej zmiennej do modelu.
do przedziału od -2 do 2. Wartości dodatnie współczynników świadczą o korzystnej reklasyfikacji, a ujemne o niekorzystnej reklasyfikacji na skutek dołożenia nowej zmiennej do modelu.
Test Z do sprawdzania istotności współczynnika NRI
Przy pomocy tego testu badamy czy zmiana klasyfikacji wyrażona współczynnikiem  była istotna.
była istotna.
Hipotezy:
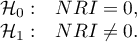
Statystyka testowa ma postać:
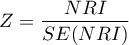
gdzie:
![LaTeX $
\begin{array}{cl}
SE(NRI)= & [\left(\frac{\#events_{up} + \#events_{down}}{\#events^2}-\frac{(\#events_{up} + \#events_{down})^2}{\#events^3}\right)+\\
& +\left(\frac{\#nonevents_{down} + \#nonevents_{up}}{\#nonevents^2}-\frac{(\#nonevents_{down} + \#nonevents_{up})^2}{\#nonevents^3}\right)]^{1/2}
\end{array}
$](/lib/exe/fetch.php?media=wiki:latex:/img4a0d14005d06df04a67c84ba7e8733d7.png)
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Zintegrowana poprawa dyskryminacji
Miara ta oznaczana jest skrótem  (ang. Integrated Discrimination Improvement). Współczynniki
(ang. Integrated Discrimination Improvement). Współczynniki  poskazuje różnicę pomiędzy wartością średniej zmiany prawdopodobieństwa przewidywanego pomiędzy grupą obiektów doświadczających zdarzenia a grupą obiektów, które zdarzenia nie doświadczyły.
poskazuje różnicę pomiędzy wartością średniej zmiany prawdopodobieństwa przewidywanego pomiędzy grupą obiektów doświadczających zdarzenia a grupą obiektów, które zdarzenia nie doświadczyły.
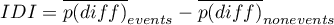
gdzie:
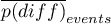 - średnia różnicy wartości prawdopodobieństwa przewidywanego między modelami regresji („starym” i „nowym”) dla obiektów, które doświadczyły zdarzenia,
- średnia różnicy wartości prawdopodobieństwa przewidywanego między modelami regresji („starym” i „nowym”) dla obiektów, które doświadczyły zdarzenia,
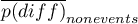 - średnia różnicy wartości prawdopodobieństwa przewidywanego między modelami regresji („starym” i „nowym”) dla obiektów, które nie doświadczyły zdarzenia.
- średnia różnicy wartości prawdopodobieństwa przewidywanego między modelami regresji („starym” i „nowym”) dla obiektów, które nie doświadczyły zdarzenia.
Test Z do sprawdzania istotności współczynnika IDI
Przy pomocy tego testu badamy czy różnica pomiędzy wartością średniej zmiany prawdopodobieństwa przewidywanego pomiędzy grupą obiektów doświadczających zdarzenia a obiektami nie doświadczającymi zdarzenia, wyrażona współczynnikiem 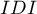 , była istotna.
, była istotna.
Hipotezy:
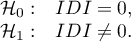
Statystyka testowa ma postać:
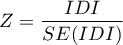
gdzie:
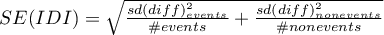
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

W programie PQStat porównywanie modeli możemy przeprowadzić ręcznie lub automatycznie.
Ręczne porównywanie modeli - polega na zbudowaniu 2 modeli:
pełnego - modelu z większą liczbą zmiennych,
zredukowanego - modelu z mniejszą liczbą zmiennych - model taki powstaje z modelu pełnego po usunięciu zmiennych, które z punktu widzenia badanego zjawiska są zbędne.
Wybór zmiennych niezależnych w porównywanych modelach a następnie wybór lepszego modelu, na podstawie uzyskanych wyników porównania, należy do badacza.
Automatyczne porównywanie modeli jest wykonywane w kilku krokach:
[krok 1] Zbudowanie modelu z wszystkich zmiennych.
[krok 2] Usunięcie jednej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.
[krok 3] Porównanie modelu pełnego i zredukowanego.
[krok 4] Usunięcie kolejnej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.
[krok 5] Porównanie modelu wcześniejszego i nowo zredukowanego.
[…]
W ten sposób powstaje wiele, coraz mniejszych modeli. Ostatni model zawiera tylko 1 zmienną niezależną.
Przykład c.d. (plik zadanie.pqs)
W eksperymencie badającym umiejętność koncentracji, dla 130 osób zbioru uczącego, zbudowano model regresji logistycznej w oparciu o następujące zmienne:
zmienna zależna: ROZWIĄZANIE (tak/nie) - informacja o tym, czy zadanie zostało rozwiązane poprawnie czy też nie;
zmienne niezależne:
MIEJSCEZAM (1=miasto/0=wieś),
PŁEĆ (1=kobieta/0=mężczyzna),
WIEK (w latach),
WYKSZTAŁCENIE (1=podstawowe, 2=zawodowe, 3=średnie, 4=wyższe),
CZAS rozwiązywania (w minutach),
ZAKŁÓCENIA (1=tak/0=nie).
Sprawdzimy, czy wszystkie zmienne niezależne są w modelu niezbędne.
- Ręczne porównywanie modeli.
Na podstawie zbudowanego wcześniej modelu pełnego możemy podejrzewać, że zmienne: MIEJSCEZAM i PŁEĆ mają niewielki wpływ na budowany model (tzn. na podstawie tych zmiennych nie możemy z sukcesem dokonywać klasyfikacji). Sprawdzimy czy, ze statystycznego punktu widzenia, model pełny jest lepszy niż model po usunięciu tych dwóch zmiennych.
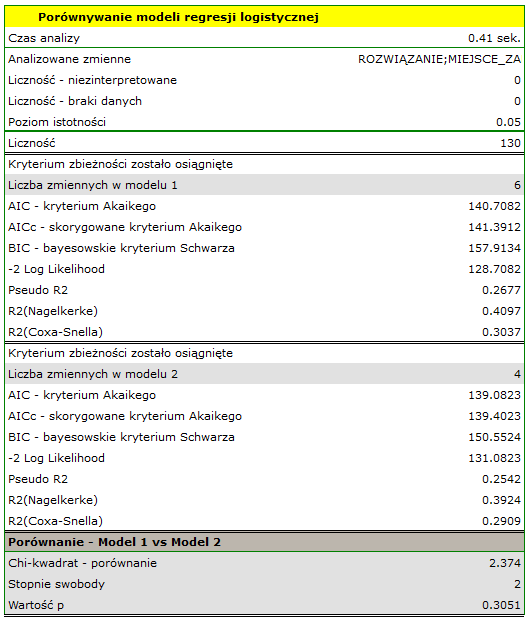
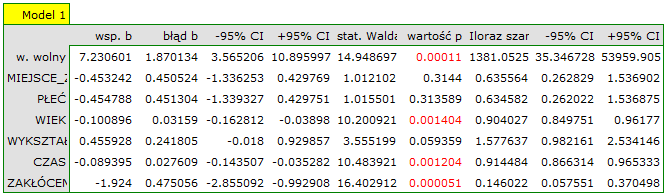
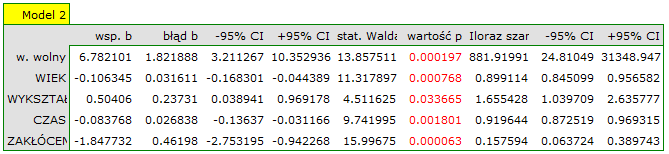
Wynik testu ilorazu wiarygodności (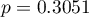 ) wskazuje , że nie ma podstaw by uważać, że model pełny jest lepszy niż model zredukowany. Zatem, przy nieznacznej utracie jakości modelu, miejsce zamieszkania i płeć mogą zostać pominięte.
) wskazuje , że nie ma podstaw by uważać, że model pełny jest lepszy niż model zredukowany. Zatem, przy nieznacznej utracie jakości modelu, miejsce zamieszkania i płeć mogą zostać pominięte.
Porównania obu modeli pod względem zdolności do klasyfikacji możemy dokonać porównując krzywe ROC dla tych modeli, wartość NRI i IDI. W tym celu wybieramy odpowiednią opcję w oknie analizy. Uzyskany raport, podobnie jak wcześniejszy, wskazuje, że modele nie różnią się jakością predykcji tzn. wartości p dla porównania krzywych ROC oraz do oceny wskaźników NRI i IDI są nieistotne statystycznie. Decydujemy zatem pominąć płeć i miejsce zamieszkania w ostatecznym modelu.

- Automatyczne porównywanie modeli.
W przypadku automatycznego porównywania modeli uzyskaliśmy bardzo podobne wyniki. Najlepszym modelem jest model zbudowany na podstawie zmiennych niezależnych: WIEK, WYKSZTAŁCENIE, CZAS rozwiązywania, ZAKŁUCENIA.
Na podstawie powyższych analiz, ze statystycznego punktu widzenia, optymalnym modelem jest model zawierający 4 najważniejsze zmienne niezależne: WIEK, WYKSZTAŁCENIE, CZAS rozwiązywania, ZAKŁUCENIA. Dokładną jego analizę możemy przeprowadzić w module Regresja Logistyczna. Jednak ostateczna decyzja, który model wybrać należy do eksperymentatora.
Badano czynniki ryzyka pewnej choroby serca takie jak wiek, bmi, palenie, cholesterol we frakcji LDL, cholesterol we frakcji HDL i nadciśnienie. Z punktu widzenia badacza interesujące było określenie jak bardzo informacja o paleniu może poprawić predykcję występowania badanej choroby.
Porównujemy model regresji logistycznej opisujący ryzyko choroby serca na podstawie wszystkich badanych zmiennych z modelem pozbawionym informacji o paleniu. W oknie analizy zaznaczamy opcje związane z oceną predykcji, czyli krzywą ROC oraz współczynniki NRI. Dodatkowo wskazujemy, by w raporcie znalazły się wszystkie proponowane wykresy.

Analiza raportu wskazuje na ważne różnice w predykcji na skutek dodania do modelu informacji o paleniu, chociaż nie są one istotne w opisie krzywej ROC (p=0.057).
Ciągłe wartości współczynnika IDI i NRI wskazują na istotną statystycznie i korzystą zmianę (wartości tych współczynników są dodatnie, a wartości p<0.05). Prognoza dla osób z chorobą serca poprawiła się o ponad 5% a osób bez tej choroby o ponad 13% (NRI(chory)=0.0522, NRI(zdrowy)=0.1333)) na skutek uwzględnienia informacji o paleniu.
Wnioski wyciągnięte na bazie NRI widzimy również na wykresie. Wzrost prognozowanego przez model prawdopodobieństwa choroby widzimy u osób chorych (więcej osób zostało przeklasyfikowanych w górę niż w dół 52.61% vs 47.39%) natomiast spadek prawdopodobieństwa dotyczy w większym stopniu osób zdrowych (więcej osób zostało przeklasyfikowanych w dół niż w górę 56.67% vs 43.33%).
Istnieje też możliwość wyznaczenia NRI kategorialnego, ale w tym celu należałoby najpierw ustalić przyjęte w literaturze dotyczącej chorób serca punkty odcięcia prawdopodobieństwa wyznaczonego przez model.
2014/08/22 20:00
ANOVA czynnikowa - GLM
Okno z ustawieniami opcji ANOVA czynnikowa GLM wywołujemy poprzez menu Statystyka→Modele wielowymiarowe→ANOVA czynnikowa GLM
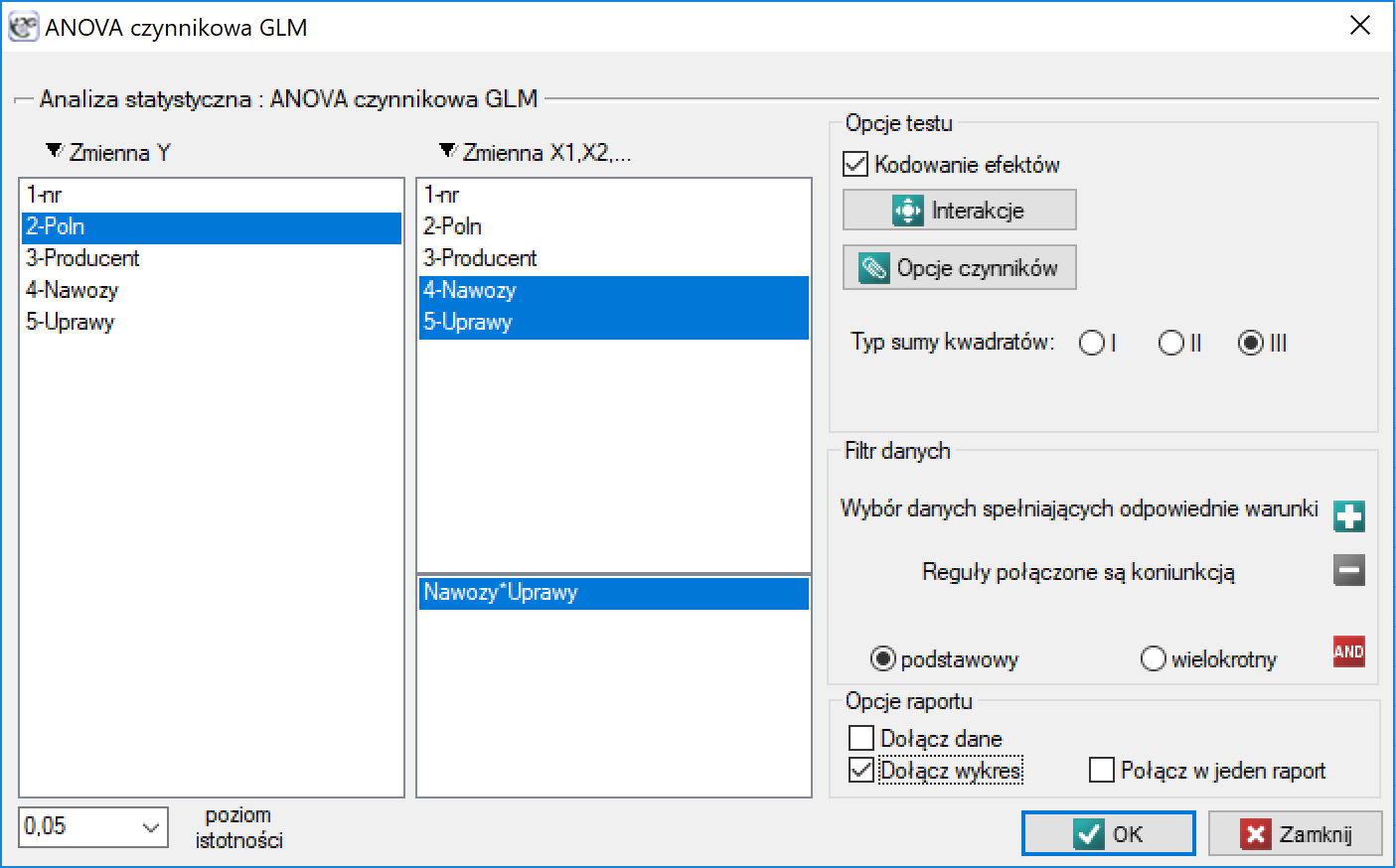

 Czynnikowa analiza wariancji GLM jest rozszerzeniem jednoczynnikowej analizy wariancji (ANOVA) dla grup niezależnych oraz liniowej regresji wielorakiej. Skrót GLM (ang. general linear model) czytamy jako Ogólny Model Liniowy. Analiza GLM polega zwykle na wykorzystaniu modeli regresji liniowej w wyliczaniu różnych złożonych porównań ANOVA.
Czynnikowa analiza wariancji GLM jest rozszerzeniem jednoczynnikowej analizy wariancji (ANOVA) dla grup niezależnych oraz liniowej regresji wielorakiej. Skrót GLM (ang. general linear model) czytamy jako Ogólny Model Liniowy. Analiza GLM polega zwykle na wykorzystaniu modeli regresji liniowej w wyliczaniu różnych złożonych porównań ANOVA.
Przykład
Przykład równoważnych analiz, które mogą być przeprowadzone poprzez GLM. Analizy zawarte w poszczególnych wierszach tabeli są równoważne w tym sensie, że ich wyniki są tożsame, choć nie muszą być identyczne.
Badanie dotyczy dochodu pewnej grupy osób. O badanych osobach mamy pewne dodatkowe informacje typu: płeć i wykształcenie.
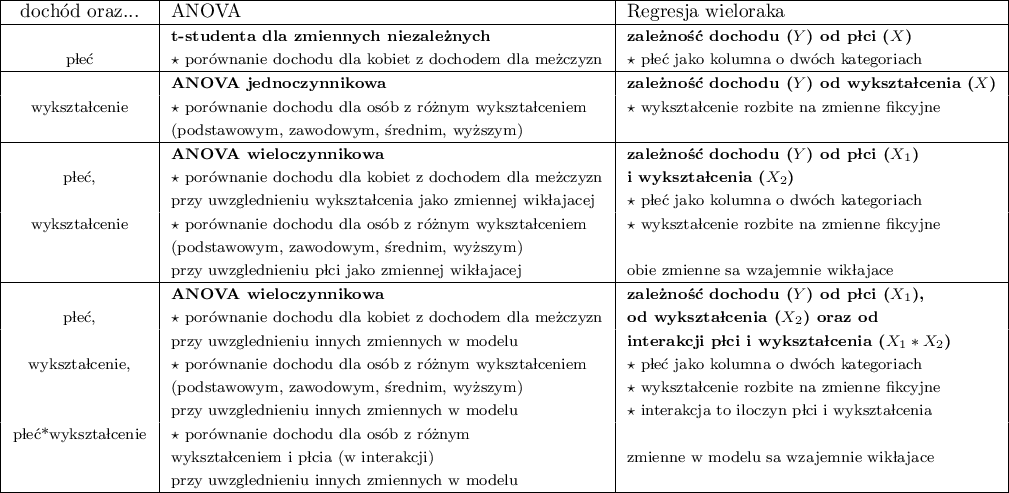
Analiza GLM może być wykorzystana w każdym z powyższych przypadków, ponieważ jednak analiza regresji wielorakiej podobnie jak jednoczynnikowa ANOVA zostały omówione w oddzielnych rozdziałach, w tym rozdziale przedstawimy wykorzystanie GLM w ANOVA wieloczynnikowa.
ANOVA czynnikowa jest takim rodzajem analizy wariancji, w którym możemy wykorzystać zarówno jedną jak i wiele czynników by wyodrębnić porównywane grupy. W analizie mogą brać udział również takie zmienne, które są interakcją wskazanych czynników. Gdy ANOVA zawiera więcej czynników niż jeden, wówczas czynniki te są wobec siebie uwikłane.
Wpływ czynników wikłających
Pomimo, że wszystkie czynniki biorące udział w analizie są wobec siebie uwikłane, to ich wpływ na istotność poszczególnych czynników można kontrolować. Istnieją trzy sposoby, przy pomocy których badając istotność poszczególnych czynników można uwzględniać wpływ zmiennych wikłających. Zależą one od sposobu wyznaczania sumy kwadratów:
- Sumy kwadratów typu I
Sumy kwadratów typu I zależą od kolejności w jakiej w modelu znajdują się poszczególne czynniki. Ten rodzaj sumy kwadratów powoduje, że istotność czynnika który interpretujemy jest korygowana o te zmienne, których kolejność w modelu była wcześniejsza, pozostałe zmienne w modelu wpływają jedynie pośrednio na wynik analizy. Na przykład: jeśli w modelu umieszczamy czynniki we wskazanej kolejności:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 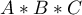 ,
,  , wówczas istotność dla czynnika
, wówczas istotność dla czynnika  uwzględnia cały model (poprzez sumy kwadratów dla błędu) ale jako zmienne wikłające wykorzystywane są wprost tylko czynniki:
uwzględnia cały model (poprzez sumy kwadratów dla błędu) ale jako zmienne wikłające wykorzystywane są wprost tylko czynniki:  ,
,  ,
,  ,
,  .
.
Sumy kwadratów dla czynnika  wylicza się wówczas następująco:
wylicza się wówczas następująco:
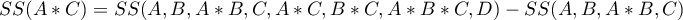
Stosowanie sumy kwadratów typu I
Wskazania: Kiedy badanie jest w pełni zbalansowane, z równymi lub proporcjonalnymi licznościami poszczególnych kategorii, również wtedy, gdy występują interakcje.
Przeciwwskazania: Kiedy badanie jest niezbalansowane (różne liczności poszczególnych kategorii) i/lub występują interakcje.
- Sumy kwadratów typu II
Ten rodzaj sumy kwadratów powoduje, że istotność czynnika który interpretujemy jest korygowana o te zmienne, których rząd jest taki sam lub niższy, pozostałe zmienne w modelu wpływają jedynie pośrednio na wynik analizy. Na przykład: jeśli w modelu umieszczamy czynniki:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 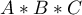 ,
, 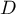 , wówczas istotność dla czynnika
, wówczas istotność dla czynnika  uwzględnia cały model (poprzez sumy kwadratów dla błędu) ale jako zmienne wikłające wykorzystywane są wprost zmienne pierwszego rzędu:
uwzględnia cały model (poprzez sumy kwadratów dla błędu) ale jako zmienne wikłające wykorzystywane są wprost zmienne pierwszego rzędu:  ,
,  ,
,  ,
, 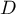 oraz wszystkie pozostałe zmienne drugiego rzędu:
oraz wszystkie pozostałe zmienne drugiego rzędu:  ,
,  .
.
Sumy kwadratów dla czynnika  wylicza się wówczas następująco:
wylicza się wówczas następująco:
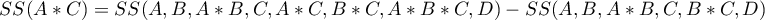
Stosowanie sumy kwadratów typu II
Wskazania: Kiedy badanie jest w pełni zbalansowane, z równymi lub proporcjonalnymi licznościami poszczególnych kategorii, również wtedy, gdy występują interakcje.
Przeciwwskazania: Kiedy badanie jest niezbalansowane (różne liczności poszczególnych kategorii) i/lub występują interakcje.
- Sumy kwadratów typu III
Zalecamy stosować ten rodzaj kodowania, gdy wybrane jest kodowanie efektów.
Ten rodzaj sumy kwadratów powoduje, że istotność czynnika który interpretujemy jest korygowana o wszystkie pozostałe zmienne w modelu. Na przykład: jeśli w modelu umieszczamy czynniki:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 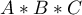 ,
, 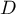 , wówczas istotność dla zmiennej
, wówczas istotność dla zmiennej  uwzględnia cały model (poprzez sumy kwadratów dla błędu) a jako zmienne wikłające wykorzystywane są wprost wszystkie czynniki za wyjątkiem badanego:
uwzględnia cały model (poprzez sumy kwadratów dla błędu) a jako zmienne wikłające wykorzystywane są wprost wszystkie czynniki za wyjątkiem badanego:  ,
,  ,
,  ,
,  ,
,  ,
, 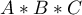 ,
,  ,.
,.
Sumy kwadratów dla czynnika  wylicza się wówczas następująco:
wylicza się wówczas następująco:
Stosowanie sumy kwadratów typu III
Wskazania: Kiedy badanie jest zbalansowane lub niezbalansowane, również wtedy, gdy występują interakcje.
Przeciwwskazania: Kiedy badanie zawiera podklasy o brakujących obserwacjach.
W PQStat domyślnie wybrane są sumy kwadratów typu III, ze względu na ich uniwersalność. Domyślnie zaznaczona jest też opcja kodowanie efektów opisana w rozdziale Przygotowanie zmiennych do analizy. Należy pamiętać, że wybór odpowiedniego kodowania wpływa zarówno na interpretację współrzędnych modelu jak i na istotność poszczególnych czynników w ANOVA czynnikowa - szczególnie przy niezbalansowanych układach.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- próby pochodzą z populacji o rozkładzie normalnym normalność zmiennych bądź reszt modelu),
- równość wariancji badanych zmiennych porównywanych populacji.
ANOVA czynnikowa wymaga by czynniki dzieliły się na poszczególne kategorie (tj. niezależne populacje) np. czynnik  : płeć dzielimy na męską i żeńską, czynnik
: płeć dzielimy na męską i żeńską, czynnik  : wykształcenie na podstawowe, zawodowe, średnie i wyższe. Interakcja czynnika
: wykształcenie na podstawowe, zawodowe, średnie i wyższe. Interakcja czynnika  jest również dzielona na kategorie, w tym przypadku kategorii uzyskamy osiem:
jest również dzielona na kategorie, w tym przypadku kategorii uzyskamy osiem:
1) kategoria żeńska z wykształceniem podstawowym,
2) żeńska z wykształceniem zawodowym,
3) żeńska z wykształceniem średnim,
4) żeńska z wykształceniem wyższym,
5) kategoria męska z wykształcniem podstawowym,
6) męska z wykształceniem zawodowym,
7) męska z wykształceniem średnim,
8) męska z wykształceniem wyższym.
Analiza typu ANOVA i modele regresji traktowane są równoważnie, i w ogólnym przypadku ich hipotezy są zbieżne. Hipotezy dla efektów głównych  i
i  i efektu interakcji
i efektu interakcji  przedstawimy w obu tych ujęciach. W interpretacji tych hipotez należy pamiętać, że hipotezy dla danych czynników korygowane są o te z pozostałych czynników, które dana analiza uwzględnia.
przedstawimy w obu tych ujęciach. W interpretacji tych hipotez należy pamiętać, że hipotezy dla danych czynników korygowane są o te z pozostałych czynników, które dana analiza uwzględnia.
Podejście ANOVA
Hipotezy dla czynnika  :
:
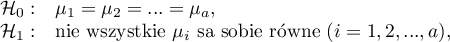
gdzie:
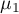 ,
,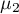 ,…,
,…,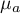
 średnie czynnika
średnie czynnika  dla poszczególnych jego kategorii.
dla poszczególnych jego kategorii.
Hipotezy dla czynnika  :
:
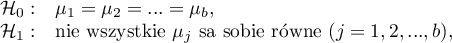
gdzie:
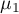 ,
,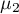 ,…,
,…,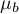
 średnie czynnika
średnie czynnika  dla poszczególnych jego kategorii.
dla poszczególnych jego kategorii.
Hipotezy dla interakcji czynników  :
:
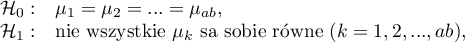
gdzie:
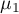 ,
,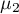 ,…,
,…,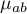
 średnie interakcji czynników
średnie interakcji czynników  dla poszczególnych ich kategorii.
dla poszczególnych ich kategorii.
Podejście regresyjne
Podejście modelowe zakłada działanie modelu regresji
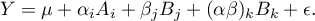
gdzie:
 - zmienna zależna, objaśniana przez model,
- zmienna zależna, objaśniana przez model,
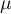 - średnia ogólna zmiennej
- średnia ogólna zmiennej  (o ile zastosowano kodowanie efektów)
(o ile zastosowano kodowanie efektów)
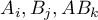 - czynniki - zmienne niezależne, objaśniające,
- czynniki - zmienne niezależne, objaśniające,
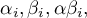 - parametry,
- parametry,
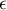 - składnik losowy (reszta modelu).
- składnik losowy (reszta modelu).
Hipotezy dla czynnika  :
:
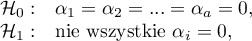
Hipotezy dla czynnika  :
:
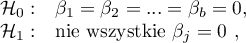
Hipotezy dla interakcji czynników  :
:
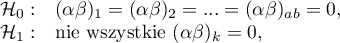
Kodowanie
Uzyskiwane wyniki analiz (w szczególności budowanego modelu regresji) oraz interpretacja hipotez zależą również od sposobu kodowania. Program PQStat oferuje kodowanie zero-jedynkowe i kodowanie efektów. Dokładny opis kodowania można znaleźć w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych. Domyślnie program wybiera kodowanie efektów. Odznaczenie tej opcji jest równoważne z wybraniem kodowania zero-jedynkowego.
Uwaga!
W przypadku stosowaniu sumy kwadratów typu III, gdy występują interakcje, wskazane jest stosowanie kodowania efektów.
Aby zwiększyć plon roślin uprawnych, opracowuje się nawozy według coraz nowszych technologii. Na podstawie przeprowadzonego eksperymentu badacze chcą się dowiedzieć, która z trzech mieszanek nowych nawozów jest najbardziej skuteczna. Uprawy były prowadzone przez dwa różne gospodarstwa rolne i dotyczyły zasiewu pszenicy, żyta, owsa i jęczmienia. Plon podawano w % (w porównaniu do plonu uzyskanego bez nawożenia).
W pierwszej kolejności chcemy sprawdzić czy:
1) H0: Średnie plony uzyskane przy zastosowaniu nawożenia mieszanką X są takie same jak uzyskane przy nawożeniu mieszanką Y i takie same jak przy nawożeniu mieszanką Z (niezależnie od gospodarstwa prowadzącego uprawę).
Ponadto, choć jest to w tym przypadku miej interesujące, sprawdzimy czy:
2) H0: Średnie plony uzyskane w gospodarstwie 1 są takie same jak w gospodarstwie drugim (niezależnie od mieszanki stosowanego nawozu).
Równoważnie hipotezy te można zapisać korzystając z podejścia regresyjnego:
1) H0: Współczynniki określające zmianę uzyskanego plonu przy zmianie stosowanego nawożenia są zerowe (niezależnie od gospodarstwa prowadzącego uprawę).
2) H0: Współczynnik określający zmianę uzyskanego plonu przy zmianie gospodarstwa prowadzącego uprawę jest zerowy (niezależnie od mieszanki stosowanego nawozu).
W drugiej kolejności stosując GLM sprawdzimy czy:
3) H0: Średnie plony uzyskane z uprawy poszczególnych zbóż są takie same gdy stosujemy różny sposób nawożenia.
Hipotezy 1) i 2)
Podejście ANOVA
Analizę przeprowadzimy stosując trzeci typ sumy kwadratów i kodowanie efektów.
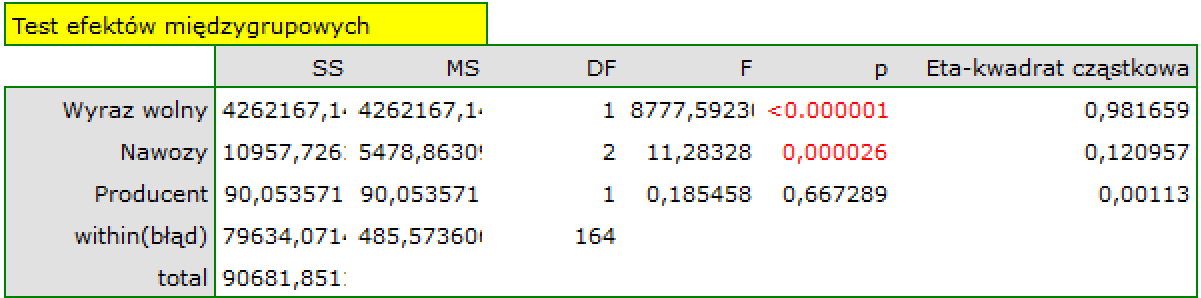
Obserwujemy istotne statystycznie różnice pomiędzy plonem uzyskanym przy zastosowaniu różnych mieszanek nawozów (p=0.000026). Zastosowana mieszanka nawozów tłumaczy zmienność w uzyskanym plonie w około 12% o czym świadczy wartość cząstkowej Eta-kwadrat. Uzyskane plony nie zależą natomiast od tego w jakim gospodarstwie prowadzono uprawy (p=0.667289, Eta-kwadrat cząstkowe = 0,1%).
Po wybraniu średnich obserwowanych lub oczekiwanych w oknie Opcji czynników, różnice te możemy przedstawić graficznie na wykresach obrazujących średnie plony przy stosowaniu poszczególnych mieszanek nawozów. Dokładne wartości średnich możemy odczytać z tabeli statystyk opisowych.
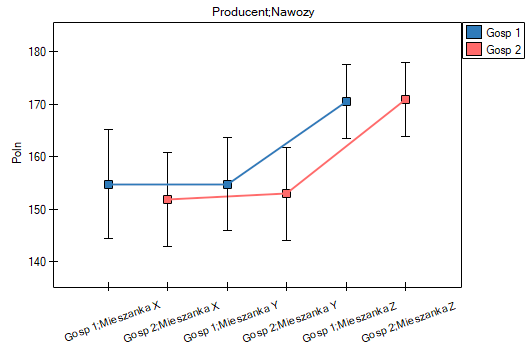
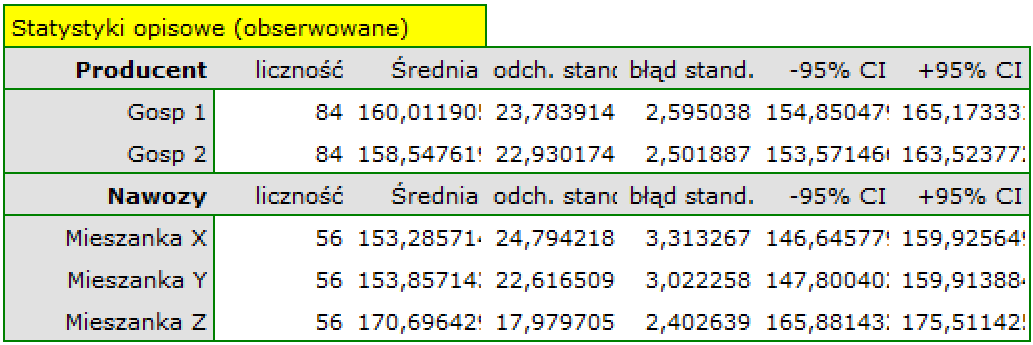
To, gdzie różnice są zlokalizowane możemy sprawdzić stosując testy post-hoc. Test post-hoc NIR Fishera wskazuje, iż najkorzystniejsze rezultaty przynosi stosowanie mieszanki Z – uzyskany plony stanowi średnio 170,7% plonu, który uzyskano by nie stosując nawożenia. Pozostałe mieszani nie różnią się istotnie statystycznie wielkością uzyskanego plonu. Ponieważ w modelu jednoczesnej analizie poddawano gospodarstwo w którym prowadzone były uprawy, możemy powiedzieć, że przewaga mieszanki Z jest niezależna od tego, w którym gospodarstwie wykonano zasiew.
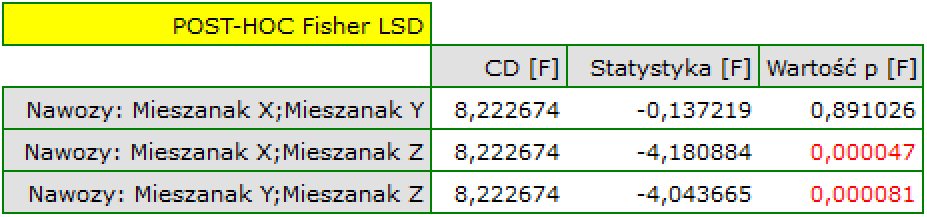
Podejście regresyjne
Analogiczną interpretację uzyskamy posługując się modelem regresji, choć tutaj interpretacja jest nieco trudniejsza. Trudność wynika z konieczności ustalenia sposobu kodowania i wyboru kategorii odniesienia. Przyjrzyjmy się najpierw wynikom otrzymanym przy kodowaniu zero-jedynkowym, które możemy uzyskać odznaczając opcję kodowania efektów. Analiza automatycznie przyjęła alfabetycznie pierwszy poziom jako poziom odniesienia. Dla nawozów poziomem tym była mieszanka X, dla gospodarstw było to gospodarstwo 1.


Analiza współczynników modelu przypomina analizę testów post-hoc, z tą różnicą, że porównujemy wyłącznie do kategorii odniesienia. Jeśli więc wszystkie mieszanki nawozów porównamy do mieszanki X możemy zauważyć, że jedynie stosując mieszankę Z uzyskano istotnie wyższe wyniki (p= 0.000047). Wyniki te są wyższe o 17.410714 (przypominam, że średnie wynosiły odpowiednio (153.285714 – dla mieszanki X, 170.696429 – dla mieszanki Z). Porównując gospodarstwa sprawa jest prosta, gdyż mamy do porównania tylko dwa gospodarstwa i uzyskany wynik jest wynikiem porównania gospodarstwa 2 z gospodarstwem 1, które to stanowiło kategorię odniesienia. Tym razem uzyskana różnica była niewielka (-1.464286) i nieistotna statystycznie (0.667289).
Stosując kodowanie efektów również wybieramy kategorię odniesienia, ale wielkość współczynników i ich istotność nie jest odnoszona do wybranej kategorii odniesienia ale do średniej ogólnej uzyskanego plonu, zapisanej w modelu jako wyraz wolny (159.279762).
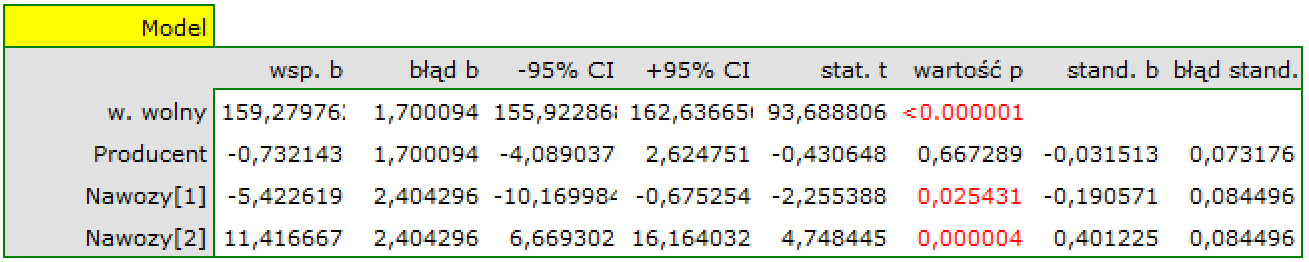
W porównaniu do średniej ogólnej znajdujemy sporo różnic: plon uzyskany przy nawożeniu mieszanką Y jest o 5.422619 niższy niż średnia ogólna, a mieszanką Z o 11.416667 wyższy. Obie różnice są istotne statystycznie.
Niepodważalną zaletą budowania modelu regresyjnego jest możliwość wykorzystania jego formuły w przewidywaniu uzyskanych plonów. Zbudowane modele prezentują się następująco:
Dla kodowania zero-jedynkowego:
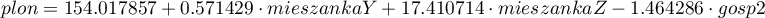
Dla kodowania efektów:
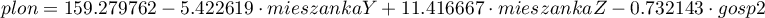
By móc zastosować wybrany model w prognozowaniu należy udać się do menu regresja wieloraka – predykcja i na podstawie nowych danych dokonać predykcji. Przy czym przygotowanie danych zależy od sposobu ich kodowania.
Na podstawie wszystkich uzyskanych wyników nie podejrzewamy by wielkość plonu była zależna od interakcji między rodzajami stosowanych nawozów a gospodarstwem prowadzącym uprawy. Najczęściej występowanie interakcji widoczne jest na wykresie w postaci wyraźnie przecinających się linii. Tu obie linie były prawie równoległe i na tyle bliskie sobie, że różnica między gospodarstwami była nieistotna statystycznie. Mimo, że przecinające się linie najczęściej świadczą o występowaniu interakcji należy pamiętać, żę gdy linie znajdują się blisko siebie ich przypadkowe przecięcie jest bardzo prawdopodobne, w efekcie tego interakcja nie będzie istotna statystycznie. Dla pewności sprawdzimy jednak, czy w naszym przypadku występuje interakcja. W tym celu obie zmienne wybierzemy raz jeszcze w oknie interakcji i przeniesiemy do listy interakcji umieszczonej po prawej stronie okna a następnie powtórzymy analizę.
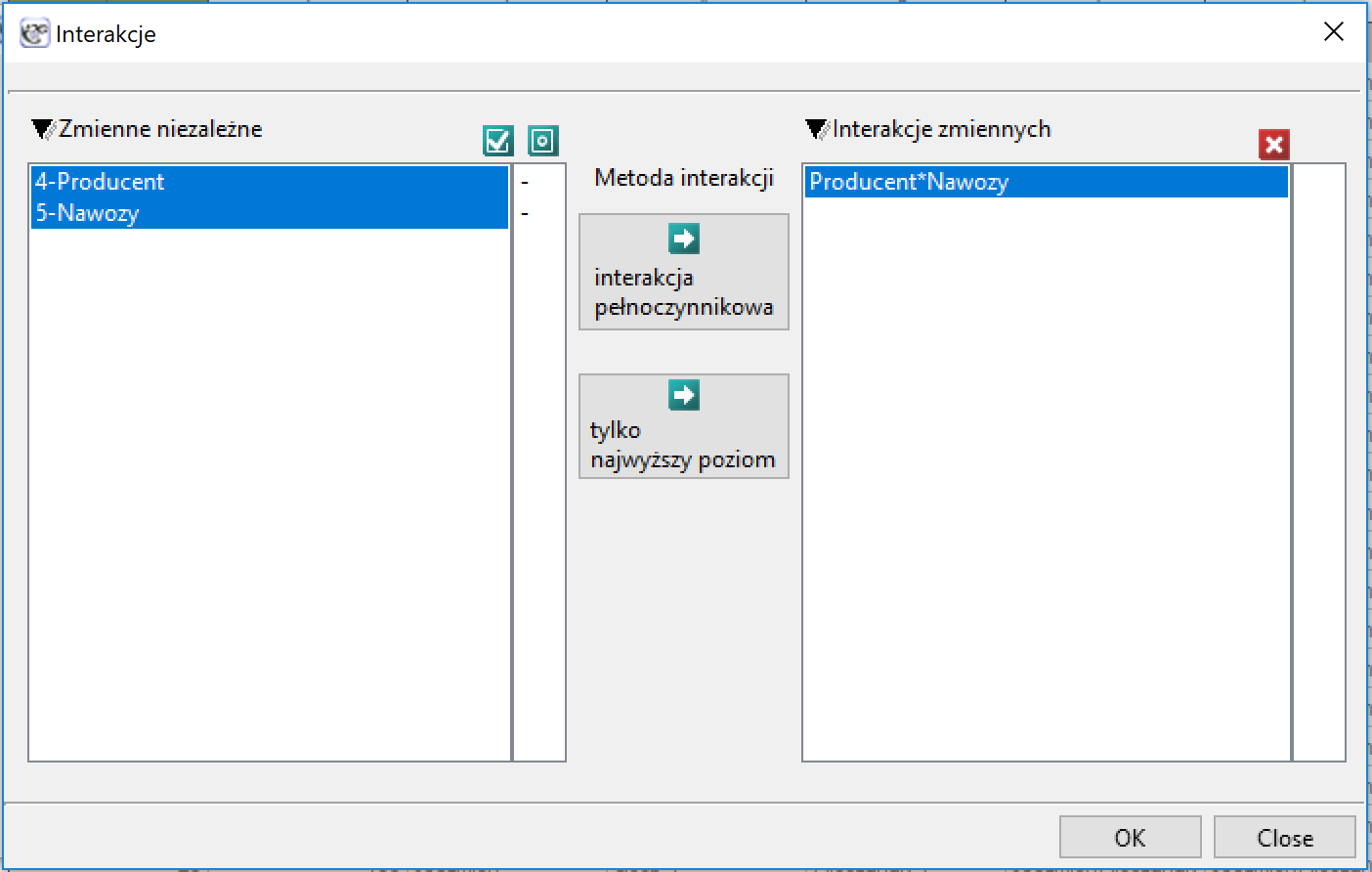
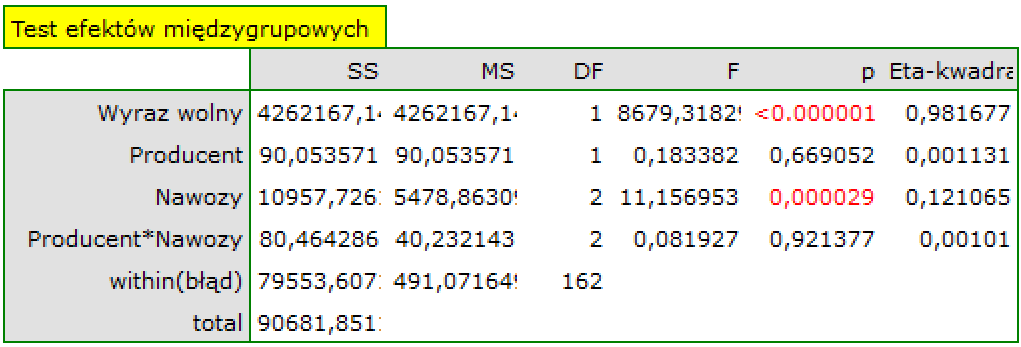
Uzyskany wynik potwierdził nasze przypuszczenia o braku istotnej interakcji (p=0.921377). W tym wypadku zaleca się więc stosowanie modelu prostszego, tzn. pozbawionego interakcji.
Hipoteza 3)
Z odmienną sytuacją zetkniemy się badając wielkość uzyskanego plonu w zależności od stosowanej dawki nawozu oraz w zależności od rodzaju uprawianego zboża.
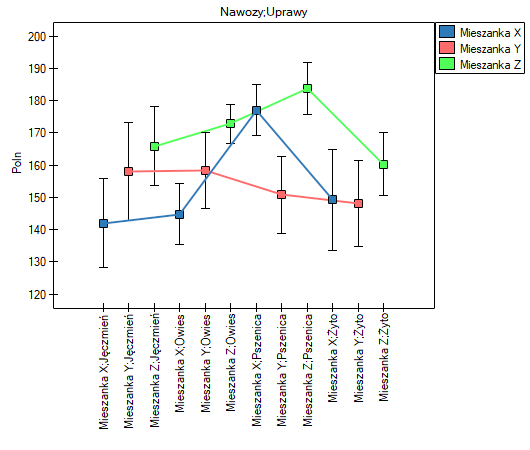
Wykonamy analizę która oprócz efektów głównych uwzględnia interakcje.
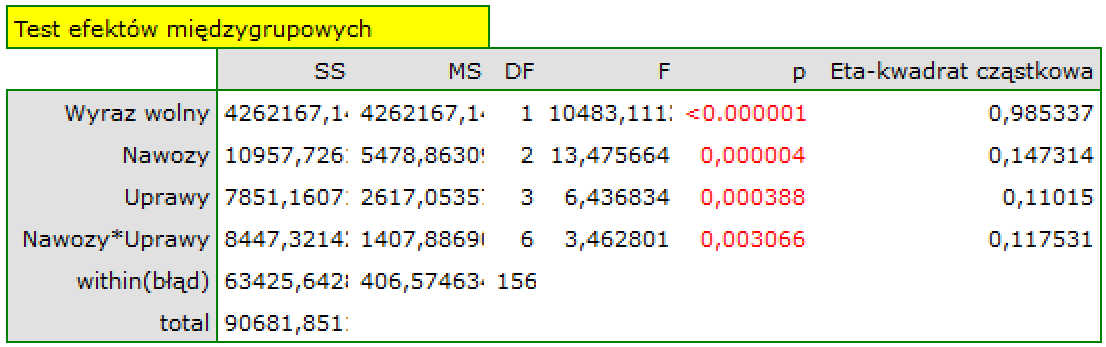
Ponieważ interakcje w zbudowanym modelu są istotne statystycznie (p=0.003066), to właśnie model z interakcjami powinniśmy stosować i opis uzyskanych wyników skupić właśnie na tej interakcji.
W podejściu ANOVA hipoteza odnosząca się do interakcji dotyczy wszystkich możliwych par średnich, tzn.:
H0: Średnie plony uzyskane przy nawożeniu pszenicy mieszanką X są takie same jak przy nawożeniu pszenicy mieszanką Y i takie same jak przy nawożeniu pszenicy mieszanką Z i takie same jak przy nawożeniu żyta mieszanką X i takie same jak przy nawożeniu żyta mieszanką Y i takie same jak przy nawożeniu żyta mieszanką Z i takie same jak przy nawożeniu owsa mieszanką X i takie same jak przy nawożeniu owsa mieszanką Y i takie same jak przy nawożeniu owsa mieszanką Z i takie same jak przy nawożeniu jęczmienia mieszanką X i takie same jak przy nawożeniu jęczmienia mieszanką Y i takie same jak przy nawożeniu jęczmienia mieszanką Z.
W podejściu regresyjnym powiemy, że:
H0: Współczynniki określające zmianę uzyskanego plonu przy zmianie stosowanego nawożenia i zmianie rodzaju uprawy są zerowe.
Na podstawie wykresu (oraz średnich zapisanych w tabeli) widzimy iż zdecydowanie najlepsze plony przynosi mieszanka Z, niezależnie od rodzaju uprawianego zboża.

Natomiast mieszanka X i mieszanka Y uzyskują gorsze plony od mieszanki Z i dodatkowo zachodzi między nimi efekt interakcji. Przejawia się ona tym, że uprawa pszenicy przynosi nietypowo wysoki plon w przypadku zastosowania mieszanki X w porównaniu do plonu pszenicy uzyskanego przy nawożeniu Y, podczas gdy uprawa jęczmienia i owsa lepiej plonują, gdy stosowana jest mieszanka Y. Dokładniej uzyskane różnice możemy sprawdzić wykonując testy post-hoc. Fragment tego raportu zamieszczono poniżej:
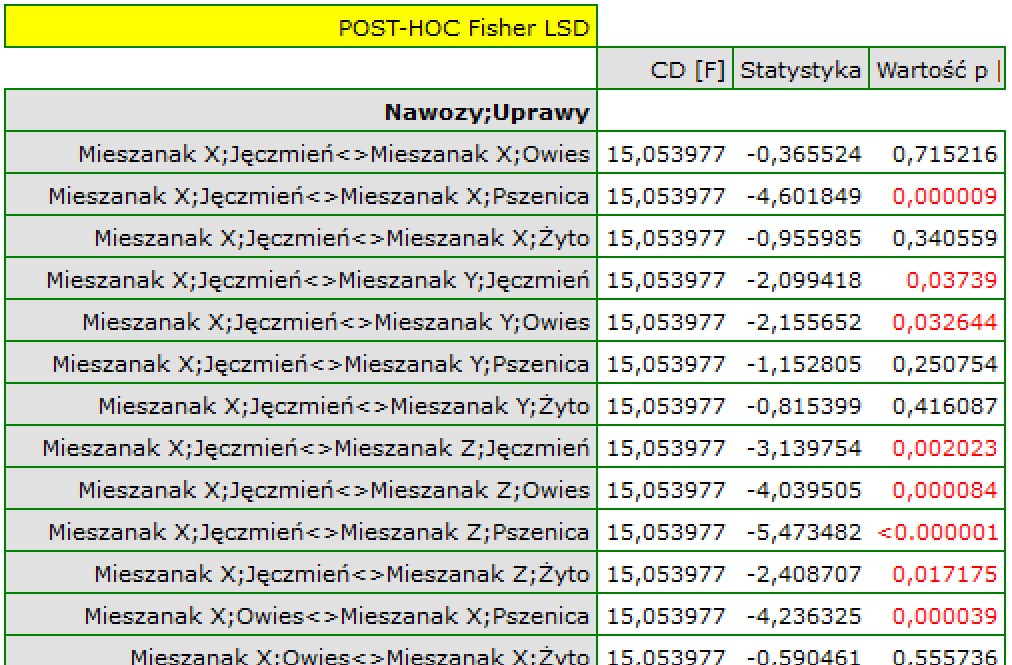
Wynik testu post-hoc Fishera jest obszerny i potwierdza dużą i istotną statystycznie przewagę uzyskanego plonu przy stosowaniu mieszanki Z dla dowolnych upraw i mieszanki Y dla uprawy pszenicy.
Współczynniki modelu regresji możemy wykorzystać do prognozy poprzez menu regresja wieloraka – predykcja pamiętając, by w zależności od wybranego modelu odpowiednio zakodować nowe dane.
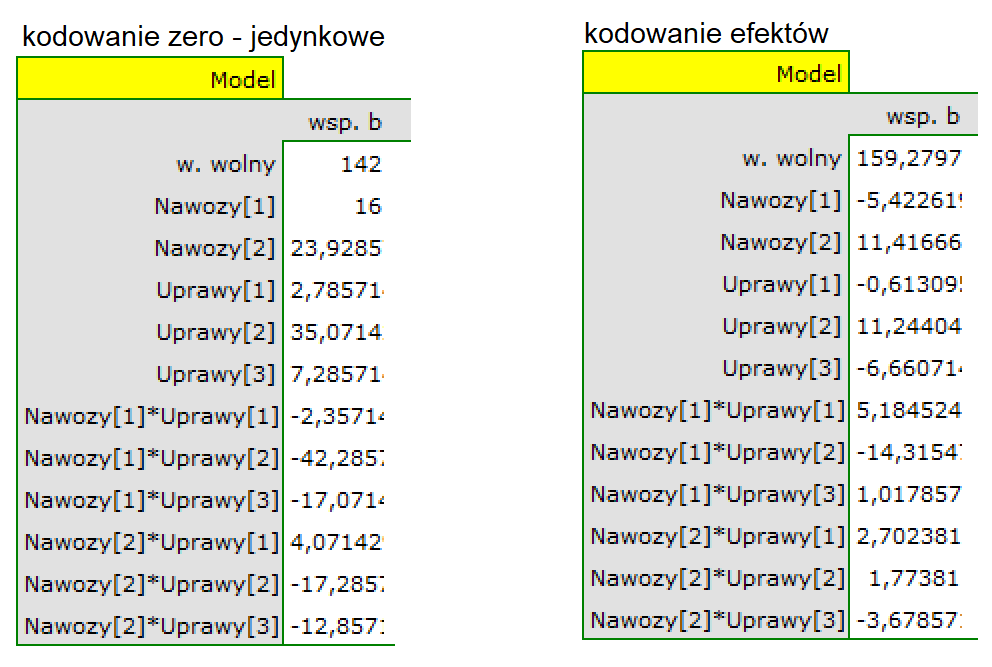
SPRAWDZENIE ZAŁOŻEŃ
Sprawdzenie głównych założeń będzie polegało na porównaniu wariacji oraz wizualnym określeniu normalności reszt modelu.
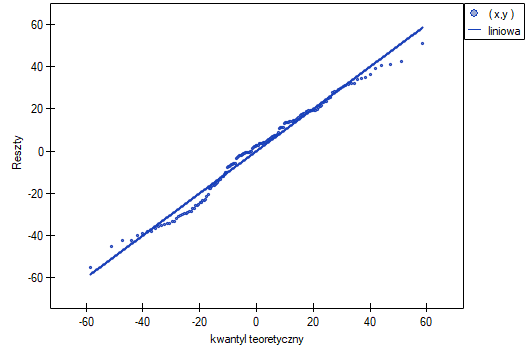
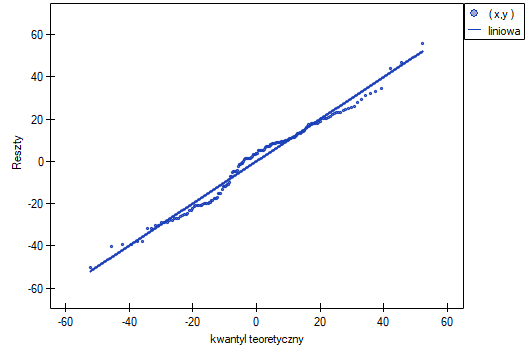
Wykres normalności reszt modelu typu Q-Q dla pierwszej oraz dla drugiej analizy przedstawia reszty modelu dobrze rozlokowane wokół prostej, co świadczy o dobrym dopasowaniu reszt do rozkładu normalnego. Porównaniu wariancji służy test Levenea lub Browna-Forsythea. W przypadku tych testów możemy założyć, że uzyskane wyniki nie są jednoznaczne i są na pograniczu równości wariancji.
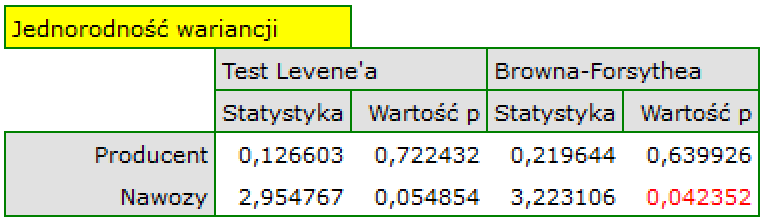
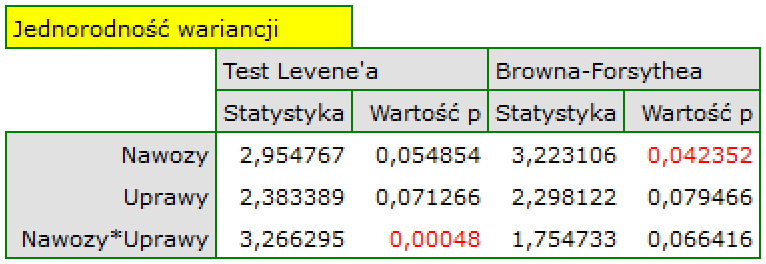
2019/02/21 13:39
· admin
ANCOVA
Analiza kowariancji (ANCOVA) jest metodą testowania hipotezy o równości średnich dwóch lub większej liczby populacji, w korekcji o inne ciągłe zmienne. Skutkiem tych korekt są efekty chętniej widziane przez badaczy niż te uzyskiwane poprzez ANOVA, tzn. węższe przedziały ufności i większa moc statystyczna.
Załóżmy, że przeprowadza się eksperyment w celu oceny efektów dwóch metod leczenia. Grupy, którym losowo przydzielono leczenie, różnią się nieco średnią wieku, która rówież wpływa na efekt leczenia. Różnice między grupami w osiągnięciach będą dość niejednoznaczne do zinterpretowania, ponieważ grupy różnią się zarówno pod względem wieku, jak i warunków leczenia. Analiza kowariancji dostarczy „skorygowanych średnich”, które szacują wartość, jaką miałyby średnie wyniki, gdyby grupy były dokładnie takie same pod względem wieku. Jednocześnie zmienność wyników w obrębie grupy, wynikająca ze zmiennej (wiek), zostanie usunięta ze zmienności błędu, aby zwiększyć precyzję testu różnic między skorygowanymi średnimi.
Oznaczenie „analiza kowariancji” jest obecnie postrzegane jako anachroniczne przez niektórych metodologów badań i statystyków, ponieważ analiza ta nie jest odrębną analizą ale wariantem ogólnego modelu liniowego (GLM). Jednak termin ten jest nadal użyteczny, ponieważ natychmiast przekazuje większości badaczy pojęcie, że zmienna kategorialna (np. warunki leczenia) i zmienna ciągła (np.wiek) są zaangażowane w jedną analizę określającą wynik leczenia.
Okno z ustawieniami opcji ANCOVA wywołujemy poprzez menu Statystyka→Modele wielowymiarowe→ANCOVA
Uwaga!!!
Sposób uwzględniania badanych czynników i zmiennych wikłających opisany jest w rozdziale dotyczącym wieloczynnikowej ANOVA (Wpływ czynników wikłających). Polecanym sposobem jest wybór Sumy kwadratów typu III oraz kodowania efektów
Podstawowe warunki stosowania:
- pomiar zmiennej zależnej Y na skali interwałowej,
- próby pochodzą z populacji o rozkładzie normalnym (normalność zmiennych bądź reszt modelu),
- równość wariancji reszt pomiędzy grupami uzyskanymi na bazie czynników,
- równość nachyleń linii regresji (współczynników regresji pomiędzy każdą zmienną wikłającą a zmienną zależną) dla każdego możliwego poziomu czynnika.
Uwaga!
Równość nachyleń linii regresji badana jest przy pomocy testu F porównującego model zawierający analizowane czynniki z takim samym modelem, ale powiększonym o interakcje z czynnikami wikłającymi. Istotny statystycznie wynik oznacza złamanie założenia równych nachyleń, ponieważ istotna staje się interakcja, a więc różne nachylenia prostych.
Hipotezy ANCOVA dla pojedynczego czynnika  :
:
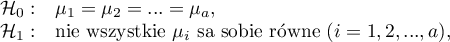
gdzie:
 ,
,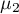 ,…,
,…,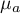 - oczekiwane średnie czynnika
- oczekiwane średnie czynnika  dla poszczególnych jego kategorii.
dla poszczególnych jego kategorii.
Hipotezy ANCOVA dla interakcji czynników  :
:
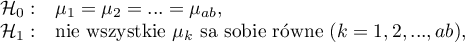
gdzie:
 ,
,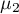 ,…,
,…,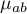 - oczekiwane średnie interakcji czynników
- oczekiwane średnie interakcji czynników  dla poszczególnych ich kategorii.
dla poszczególnych ich kategorii.
Przykład (plik lekCholesterol.pqs)
Wyobraźmy sobie, że badacz prowadził badanie nad nowym lekiem obniżającym poziom cholesterolu. Badanie było tak zaprojektowane, że dawka leku występowała na trzech poziomach: wysoka, niska i placebo. Badacz sprawdził (przy pomocy ANOVA niezależna) czy cholesterol po leczeniu różnił się w zależności od dawki leku.
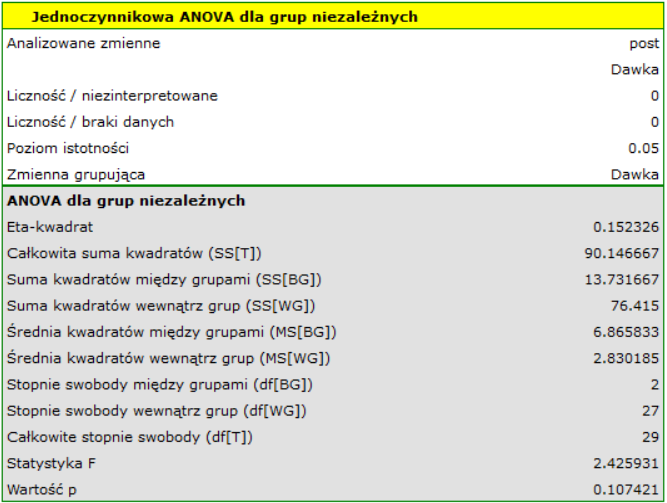
Niestety badacz nie uzyskł potwierdzenia różnic pomiędzy wynikami.
Wyobraźmy sobie, że badacz, zdał sobie sprawę, że to, czy dany lek zmieni poziom cholesterolu może być związane z wyjściowym poziomem cholesterolu oraz z wiekiem pacjenta. Z tego względu zdecydował się wykonać jednoczynnikową ANCOVA (czynnik to dawka leku) uwzględniającą jako współzmienną poziom cholesterolu przed leczeniem i wiek.
Tym razem wynik ANOCVA wskazał na występowanie istotnych różnic pomiędzy poziomem cholesterolu po zastosowaniu różnych dawek leku (p=0.00003):
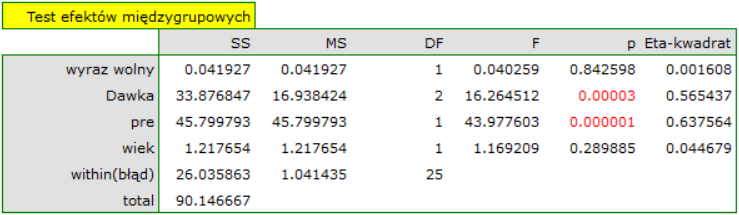
Uwzględnienie poziomu cholesterolu przed badaniem zmniejszyło uzyskiwane błędy dla średnich i zawęziło przedziały ufności. By wyświetlić obserwowane lub oczekiwane średnie, wybieram odpowiednie ustawienia poprzez Opcje czynników, do tego zaznaczam wykres błędów. Pierwszy wykres przedstawia obserwowane średnie wraz z przedziałem ufności, tzn. nie uwzględniajace wypływu wieku i poziomu cholesterolu przed leczeniem; drugi wykres to oczekiwane na podstawie zbudowanego modelu średnie wraz z przedziałami ufności, tzn. po uwzględnieniu oddziaływania tych dwóch wspólzmiennych:
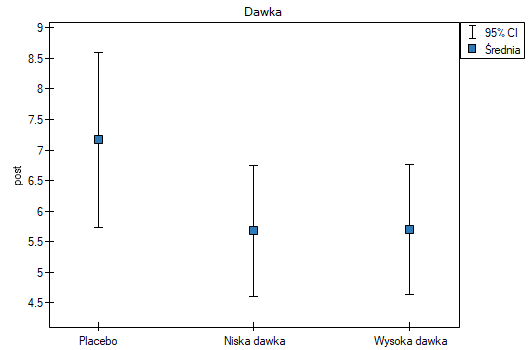
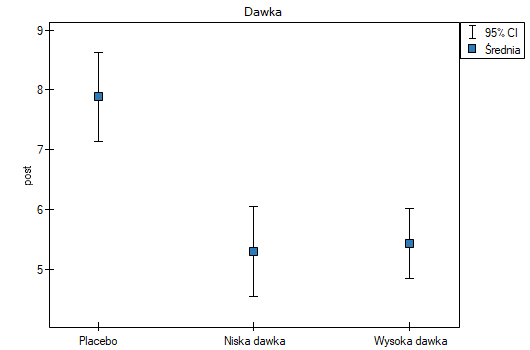
W efekcie uwzględniając poziom cholestrolu przed leczeniem badacz był w stanie wykazać skuteczność nowego sposobu leczenia. Poziom cholesterolu przed leczeniem i wiek tłumaczy w pewnym stopniu zmiany w poziemie cholesterolu po leczeniu, jednak pozostałą część zmian w 57% możemy przypisać zastosowanej dawce leku (cząstkowa Eta-kwadrat =0.565437). Testy post-hoc (wybrany poprzez Opcje czynników) zasugerowały powstanie dwóch grup jednorodnych, grupy placebo i grupy pacjentów z lekiem, wskazując że podnoszenie dawki do wysokiej nie ma znaczenia, gdyż uzyskane poziomy cholesterolu będą podobne.
Pozostały do sprawdzenia założenia ANCOVA. Jednorodność wariancji i stałość nachleń prostych regresji potwierdzono przy pomocy testów
Normalność rozkładu reszy oceniono wizualnie wyrysowując wykresy Q-Q:
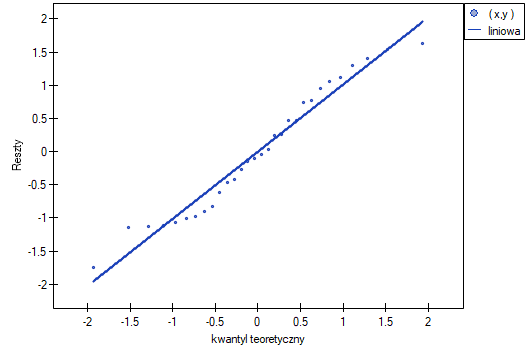
Przykład pochodzi z pakietu Datarium R-Cran.
Badacze chcą ocenić wpływ nowego leczenia i ćwiczeń na redukcję stresu po uwzględnieniu różnic w wieku. Wartość pomiaru stersu to interwałowa zmienna wynikowa Y. Ze względu na to, że zmienne „leczenie” i „ćwiczenia” mają odpowiednio 2 i 3 kategorie, przeprowadzimy dwukierunkową ANCOVA w celu określenia, czy interakcja między ćwiczeniami i leczeniem, przy jednoczesnym uwzględnieniu wieku badanych, ma związek ze stresem.
W oknie analizy jako zmienną zależną ustawiam „stres”, jako czynniki „leczenie” i „ćwiczenia” oraz dodaję interakcję tych dwóch zmiennych, współzmienna ciągła to „wiek”.
Uzyskany wynik pokazuje, że wpływ leczenia na stres zmienia się w zależności od intensywności wykonywania ćwiczeń - wskazuje na to istotna interakcja obu tych zmiennych (p=0.016409). Wyrysujemy wykres przedstawiający oczekiwane średnie poziomy stresu dla każdej z sześciu podgrup, na jakie interakcja podzieliła nasze dane oraz wyznaczymy testy post-hoc.
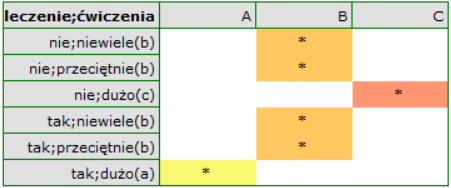
Zogodnie z wynikami testu post-hoc, możemy mówić o trzech różnych grupach jednorodnych: (B) grupa osób o wysokim poziomie stresu, to grupa ćwicząca niewiele lub przeciętnie (bez względu na to czy są to sosoby leczone czy nie), (C) grupa osób o niższym poziomie stresu, to grupa ćwicząca dużo i nieleczona, (A) grupa osób o najniższym poziomie stresu, to grupa ćwicząca dużo i leczona. Wartości poszczególnych średnich wraz z przedziałami ufności przedstawia tabela
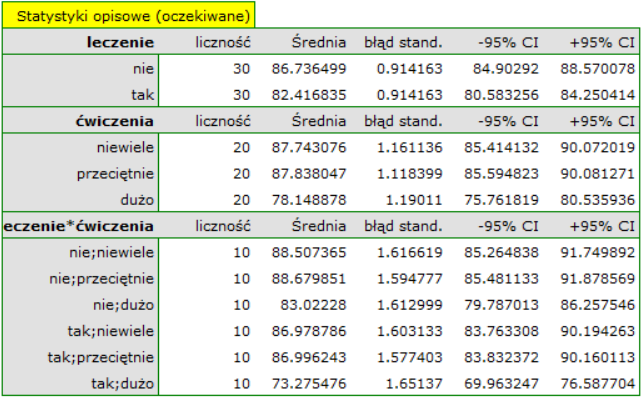
Założenia dotyczące równości wariancji, nachyleń linii regresji oraz normalności reszt modelu są spełnione
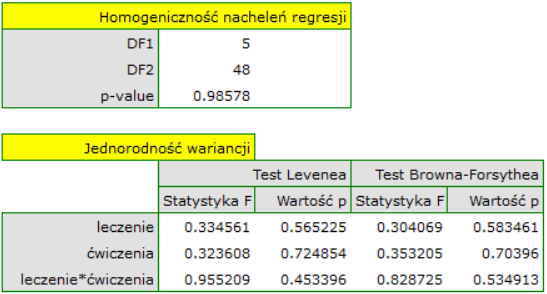
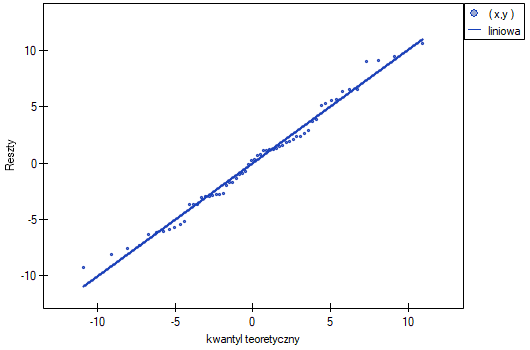
2023/03/31 19:19
· admin
Efekt mediacji
Baron i Kenny (1986)9) zdefiniowali mediatora (M) jako zmienną wyjaśniającą w istotny sposób relację między zmienną niezależną (X) a zmienną wynikową (Y). W mediacji zakłada się, że związek między zmienną niezależną a zmienną zależną jest efektem pośrednim, który istnieje dzięki wpływowi trzeciej zmiennej (mediatora).
![LaTeX \begin{pspicture}(-0.5,-0.5)(4,3.5)
\psline{->}(0.2,3)(2.8,3)
\rput(-2,3){\scriptsize model jednowymiarowy}
\rput(0,2.8){\scriptsize \textbf{X}}
\rput(3,2.8){\scriptsize \textbf{Y}}
\rput(1.5,2.7){\scriptsize $\tau$}
\rput(-2,0){\scriptsize model wielowymiarowy}
\rput(0,0){\scriptsize \textbf{X}}
\rput(3,0){\scriptsize \textbf{Y}}
\rput(1.5,2){\scriptsize \textbf{M}}
\psline[linewidth=0.7pt, linestyle=dotted]{->}(0.2,0.2)(1.2,1.8)
\psline[linewidth=0.7pt, linestyle=dotted]{->}(1.8,1.8)(2.8,0.2)
\psline{->}(0.2,0)(2.8,0)
\rput(0.4,1){\scriptsize \textit{a}}
\rput(2.6,1){\scriptsize \textit{b}}
\rput(1.5,-0.2){\scriptsize $\tau'$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgc6731b2b460c05170e52c145f6f67b4b.png)
Wielkość zmian określamy poprzez różnicę współczynników opisujących związek zmiennej X ze zmienną Y w modelu jednowymiarowym:
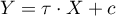
i w modelu wielowymiarowym, czyli uwzględniającym zmienną M:
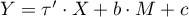 .
.
Różnica:
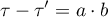
Efekt mediacji:
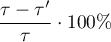
W rezultacie, gdy mediator (M) jest włączony do modelu regresji określającego związek zmiennej X i Y, wpływ zmiennej niezależnej 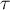 jest zmniejszony do
jest zmniejszony do 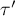 .
.
Testy oceniające efekt mediacji
Test Sobela (1982)10), test Aroiana (1947)11) spopularyzowany przez Barona i Kennyiego 12) oraz test Goodmana (1960)13) są testami, które określają, czy zmniejszenie wpływu zmiennej niezależnej na zmienną wynikową, po uwzględnieniu mediatora w modelu, jest znaczną redukcją, a zatem czy efekt mediacji jest istotny statystycznie.
Hipotezy:
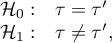
Statystyka testowa dla testu Sobela ma postać:
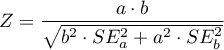
Statystyka testowa dla testu Aroiana ma postać:
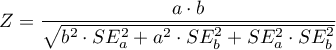
Statystyka testowa dla testu Goodmana ma postać:
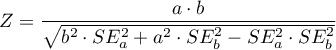
Statystyki te mają asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Test Sobela, jak też test Aroiana i Goodmana, są to testy bardzo konserwatywne i przeznaczone jedynie dla dużych prób (przekraczających 100 elementów).
Okno Analizy efektu mediacji wywołujemy poprzez:
Statystyki zaawansowane→Modele wielowymiarowe→Efekt mediacji.
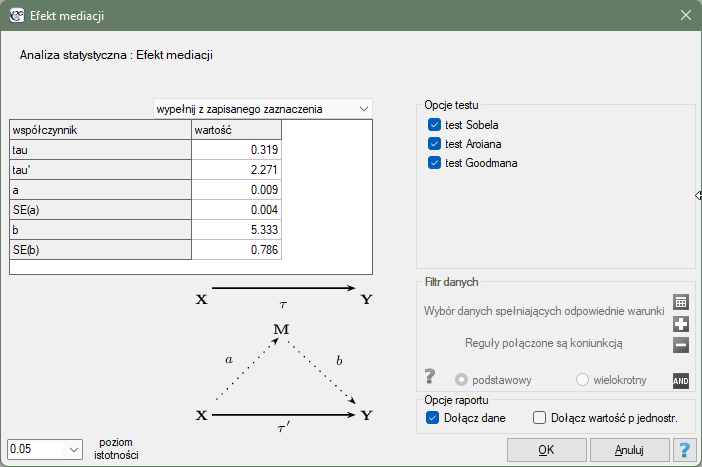
Na podstawie pracy Mimar Sinan Fine (2017) 14).
Badanie obejmuje 300 osób dorosłych mieszkających w Stambule. Zmienna zależna Y to ciśnienie skurczowe, a zmienna niezależna X to wiek. Zmienna pośrednicząca M to częstotliwość spożywania alkoholu. Celem pracy jest zbadanie zależności między wiekiem a skurczowym ciśnieniem krwi oraz przedstawienie wpływu częstości spożywania alkoholu na tę zależność.
- Zbudowano model jednowymiarowy, w którym nie uwzględniono potencjalnego mediatora:
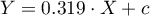 .
.
Wielkość wpływu zmiennej X (wiek) na zmienną Y (ciśnienie skurczowe) wyniosła tau=0.319.
- Zbudowano model wielowymiarowy, w którym uwzględniono potencjalny mediator:
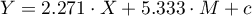 .
.
Wielkość wpływu zmiennej X (wiek) na zmienną Y (ciśnienie skurczowe) wyniosła tau'=2.271. Wiemy również z tego modelu iż b=5.333, a błąd 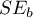 =0.786
=0.786
Różnica między współczynnikami to tau-tau'= a*b=0.048. Efekt mediacji wynosi (tau-tau')/tau=(0.319-0.271)/0.371=0.15047, co oznacza, że M (częstość spożycia alkoholu) modyfikuje badany związek zmniejszając współczynnik o około 15%.
- Zbudowano model jednowymiarowy badający wpływ zmiennej X na mediator:
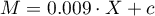 .
.
Wiemy z tego modelu, że współczynnik a=0.009, a błąd 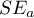 =0.004. Wszystkie te informacje wprowadzamy w oknie analizy uzyskując następujący raport:
=0.004. Wszystkie te informacje wprowadzamy w oknie analizy uzyskując następujący raport:
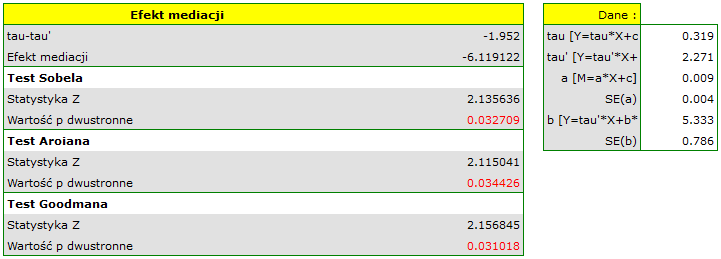
Na podstawie współczynników a i b oraz ich błędów standardowych wyznaczony zostaje wynik testów Sobela (p=0.0327), Aroiana (p=0.0344) i Goodmana (p=0.0310). Uzyskane wartości p wskazują na istotne statystycznie znaczenie mediatora. Potwierdziliśmy więc, że częstość spożywania alkoholu wpływa na związek wieku z ciśnieniem rozkurczowym na tyle zauważalnie, że warto wyjaśniać dlaczego ten efekt występuje.
2022/02/27 23:04
· admin
1)
Rosenbaum P.R., Rubin D.B. (1983a), The central role of the propensity score in observational studies for causal effects. Biometrika; 70:41–55
2)
Austin P.C., (2009), The relative ability of different propensity score methods to balance measured covariates between treated and untreated subjects in observational studies. Med Decis Making; 29(6):661-77
3)
Austin P.C., (2011), An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies. Multivariate Behavioral Research 46, 3: 399–424
4)
Normand S.L. T., Landrum M.B., Guadagnoli E., Ayanian J.Z., Ryan T.J., Cleary P.D., McNeil B.J. (2001), Validating recommendations for coronary angiography following an acute myocardial infarction in the elderly: A matched analysis using propensity scores. Journal of Clinical Epidemiology; 54:387–398.
5)
Green, S.B. (1991), How many subjects does it take to do a regression analysis? Multivariate Behavioral Research, 26, 499-510
6)
Sheather S. J. (2009), A modern approach to regression with R. New York, NY: Springer
7)
Savin N.E. and White K.J. (1977), The Durbin-Watson Test for Serial Correlation with Extreme Sample Sizes or Many Regressors. Econometrica 45, 1989-1996
8)
Peduzzi P., Concato J., Kemper E., Holford T.R., Feinstein A.R. (1996), A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol;49(12):1373-9
9)
, 12)
Baron R. M., Kenny D. A. (1986), The moderator-mediator variable distinction in social psychological research: Conceptual, strategic and statistical considerations. Journal of Personality and Social Psychology, 51, 1173-1182.
10)
Sobel M. E. (1982). Asymptotic confidence intervals for indirect effects in structural equation models. Sociological Methodology 13: 290–312
11)
Aroian, L. A. (1947), The probability function of the product of two normally distributed variables. Annals of Mathematical Statistics, 18, 265-271.
13)
Goodman L. A. (1960), On the exact variance of products. Journal of the American Statistical Association, 55, 708-713
14)
Mimar S.F. (2017), The Mediation Analysis With the Sobel Test and the Percentile Bootstrap, International Journal of Management and Applied Science, Volume-3, Issue-2
statpqpl/wielowympl.txt · ostatnio zmienione: 2023/03/31 19:19 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

