Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
przestrzenpl:autocorpl
Autokorelacja przestrzenna
By przeprowadzić analizę autokorelacji powinniśmy dysponować danymi mapy zawierającej obiekty typu: punkt, wielopunkt lub wielokąt. W przypadku analizy wielokątów bazujących na odległościach obiektów obliczenia oparte są na centroidach, a przypadku wielopunktów na centrach obiektów.
Analiza zjawiska autokorelacji przestrzennej opiera się na wartościach przypisanych obiektom przestrzennym. Autokorelacja przestrzenna oznacza, że wartości obiektów bliskich geograficznie są bardziej podobne do siebie niż tych odległych. Zjawisko to powoduje tworzenie się klasterów przestrzennych o wartościach podobnych.
Autokorelacja przestrzenna może nie występować – mówimy wówczas o przestrzennej losowości. Uzyskany rozkład przestrzenny jest tak samo prawdopodobny jak w każdy inny rozkład. Gdy wartości sąsiednie są sobie podobne, to możemy mówić o występowaniu autokorelacji dodatniej. Ujemna autokorelacja występuje wówczas, gdy wartości obszarów sąsiednich są bardziej różne niż mogłoby to wynikać z rozkładu losowego.
![LaTeX \begin{tabular}{|c|c|c|c|c|c|c|c|}
\hline
\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img68a426625e21eac96bc95dd86ad8f7b3.png)
![LaTeX \begin{tabular}{|c|c|c|c|c|c|c|c|}
\hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img26f0886654fcd30b420697eb2be83e4b.png)
![LaTeX \begin{tabular}{|c|c|c|c|c|c|c|c|}
\hline
\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i\\ \hline
\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i&\textcolor[rgb]{1,1,1}i\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\multicolumn{1}{| >{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}&\multicolumn{1}{>{\columncolor[rgb]{0.8,0.8,0.8}}l|}{\textcolor[rgb]{0.8,0.8,0.8}i}\\ \hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/imge3a989277fc70680b65665c5dfb8945a.png)
![LaTeX \begin{pspicture}(1,-1)(12.5,0)
\psline[linewidth=3pt]{<->}(-0.7,-0.5)(14,-0.5)
\rput(1.2,-1){autokorelacja ujemna}
\rput(6.6,-1){brak autokorelacji}
\rput(12.2,-1){autokorelacja dodatnia}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img04be4bd238b68bcb55e1b0b8c1ce1937.png)
Analizując autokorelację możemy rozważać zmienną dychotomiczną (tzn. występowanie lub brak danej cechy) lub zmienną o wielu kategoriach wskazującą na stopień intensywności analizowanej cechy.
Dla zmiennej dychotomicznej analiza dodatniej autokorelacji polega na wyszukiwaniu skupisk jednakowych wartości. Na płaszczyźnie mapy zwykle obiekty, w których występuje badane zjawisko oznaczone są kolorem czarny a jego brak kolorem białym. Wyszukiwane są skupiska obiektów o takim samym kolorze tzw. „black-black”,„white-white”.
Dla zmiennej opisującej stopień intensywności badanej cechy, analiza dodatniej autokorelacji polega na wyszukiwaniu skupisk podobnych wartości. Na płaszczyźnie mapy zwykle obiekty kolorowane są zgodnie ze stopniem nasilenia badanego zjawiska od najjaśniejszych (niskich wartości) do najciemniejszych (wysokich wartości) . Wyszukiwane są skupiska obiektów o podobnym odcieniu.
Statystyka globalna Morana
Jest to analiza, która bada stopień intensywności danej cechy w obiektach przestrzennych.
Do budowy współczynnika, który pozwoli sprawdzić czy sąsiadujące obiekty tworzą klastery o podobnych wartościach zmiennej, wykorzystujemy dwie informacje:
- informacje o wartościach zmiennej dla poszczególnych obiektów
 ,
, - informacje o tym, które obiekty sąsiadują – macierz wag o elementach
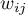 .
.
Uwaga!
Sąsiedztwo obiektów definiowane jest poprzez macierz wag. W oknie analizy Morana możemy wybrać dowolną macierz wag wygenerowaną wcześniej za pomocą menu Analiza przestrzenna → Narzędzia → Macierz wag przestrzennych lub wskazać proponowaną przez program macierz sąsiedztwa według wspólnej granicy – Queen, standaryzowaną rzędami.
Uwaga!
Nie zaleca się przeprowadzania analizy Morana dla obiektów nie posiadających sąsiedztwa (obiektów opisanych w macierzy wag wyłącznie wartością 0). Obiekty takie można wykluczyć z analizy dezaktywując je, lub przeprowadzić analizę wybierając inny sposób definiowania sąsiedztwa (inną macierz wag).
Współczynnik autokorelacji Morana – wprowadzony przez Morana w roku 19481).
By sprawdzić, czy wybrane obiekty są charakteryzowane przez podobne wartości zmiennej, można wykorzystać zasadę mnożenia mówiącą, że mnożenie 2 wartości tego samego znaku daje wynik pozytywny, a 2 różnych znaków wynik negatywny. Stosując tą zasadę wyliczamy 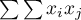 . Niestety, ze względu na to, że efekty działania tej zasady są osiągane wtedy, gdy istnieją zarówno dodatnie jak i ujemne wartości, ta prosta formuła musi być zmodyfikowana tak, by zapewnić występowanie wartości różnych znaków. Wartości zmiennej zostaną więc zastąpione we wcześniejszym wzorze przez różnice wartości zmiennej i jej wartości średniej. W ten sposób obiekty o wartościach mniejszych niż średnia będą ujemne, a te o wartościach większych od średniej dodatnie:
. Niestety, ze względu na to, że efekty działania tej zasady są osiągane wtedy, gdy istnieją zarówno dodatnie jak i ujemne wartości, ta prosta formuła musi być zmodyfikowana tak, by zapewnić występowanie wartości różnych znaków. Wartości zmiennej zostaną więc zastąpione we wcześniejszym wzorze przez różnice wartości zmiennej i jej wartości średniej. W ten sposób obiekty o wartościach mniejszych niż średnia będą ujemne, a te o wartościach większych od średniej dodatnie: 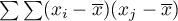 . Oczywiście sumowanie powinno dotyczyć sąsiednich obiektów, co oznacza, że musi być w tym miejscu wykorzystana informacja z macierzy wag:
. Oczywiście sumowanie powinno dotyczyć sąsiednich obiektów, co oznacza, że musi być w tym miejscu wykorzystana informacja z macierzy wag:
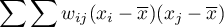 W ten sposób obiekty niesąsiadujące uzyskują wartość wagi równą 0, co powoduje, że ich wartości nie są sumowane. Dalsze zabiegi zmieniające uzyskaną w ten sposób formułę mają za zadanie uniezależnić uzyskany współczynnik
W ten sposób obiekty niesąsiadujące uzyskują wartość wagi równą 0, co powoduje, że ich wartości nie są sumowane. Dalsze zabiegi zmieniające uzyskaną w ten sposób formułę mają za zadanie uniezależnić uzyskany współczynnik 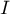 od ilości analizowanych obiektów i wystandaryzować tak, by jego wartości były ograniczone do przedziału
od ilości analizowanych obiektów i wystandaryzować tak, by jego wartości były ograniczone do przedziału 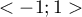 . W rezultacie współczynnik autokorelacji Morana wyraża się wzorem:
. W rezultacie współczynnik autokorelacji Morana wyraża się wzorem:
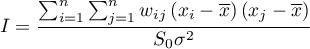
gdzie:
 – liczba obiektów przestrzennych (liczba punktów lub wielokątów),
– liczba obiektów przestrzennych (liczba punktów lub wielokątów),
 ,
, 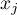 – to wartości zmiennej dla porównywanych obiektów,
– to wartości zmiennej dla porównywanych obiektów,
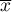 – to średnia wartość zmiennej dla wszystkich obiektów,
– to średnia wartość zmiennej dla wszystkich obiektów,
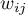 – elementy przestrzennej macierzy wag (macierz wag standaryzowana rzędami do jedynki),
– elementy przestrzennej macierzy wag (macierz wag standaryzowana rzędami do jedynki),
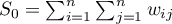 ,
,
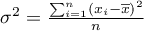 – wariancja
– wariancja
Współczynnik autokorelacji liniowej Morana 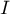 bada siłę związku liniowego pomiędzy standaryzowaną zmienną
bada siłę związku liniowego pomiędzy standaryzowaną zmienną  (
(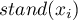 ) a opóźnieniem przestrzennym zmiennej
) a opóźnieniem przestrzennym zmiennej  (
(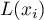 ). Opóźnienie przestrzenne (ang. spatial lag) jest średnią ważoną ze standaryzowanych wartości sąsiadujących obiektów:
). Opóźnienie przestrzenne (ang. spatial lag) jest średnią ważoną ze standaryzowanych wartości sąsiadujących obiektów:
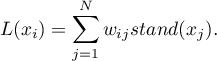
Graficzną prezentacją autokorelacji przestrzennej jest wykres rozrzutu Morana. Punkty znajdujące się w ćwiartce pierwszej (HH) i trzeciej (LL), to obiekty otoczone przez podobnych sąsiadów: HH (wysokie-wysokie) – obiekty o wysokich wartościach otoczone przez obiekty o wysokich wartościach; LL (niskie-niskie) – obiekty o niskich wartościach otoczone przez obiekty o niskich wartościach. Punkty znajdujące się w ćwiartce drugiej (LH) i czwartej (HL) to obiekty otoczone przez sąsiadów do nich niepodobnych. LH (niskie-wysokie) – obiekty o niskich wartościach otoczone przez obiekty o wysokich wartościach; HL (wysokie-niskie) – obiekty o wysokich wartościach otoczone przez obiekty o niskich wartościach.
![LaTeX \begin{pspicture}(-4,-3.6)(10,4.5)
\psline{->}(-4,0)(4,0)
\psline{->}(0,-3.5)(0,4)
\rput(1.5,1.5){\textcolor{red}{\textbf{\colorbox[rgb]{0.82,0.82,0.82}{HH}}}}
\rput(-1.5,1.5){\textcolor[rgb]{0.2,0.8,0.8}{\textbf{\colorbox[rgb]{0.82,0.82,0.82}{LH}}}}
\rput(-1.5,-1.5){\textcolor[rgb]{0,0,1}{\textbf{\colorbox[rgb]{0.82,0.82,0.82}{LL}}}}
\rput(1.5,-1.5){\textcolor[rgb]{1,0.36,0.36}{\textbf{\colorbox[rgb]{0.82,0.82,0.82}{HL}}}}
\psdot[dotsize=3pt](1.5,-0.6)
\psdot[dotsize=3pt](0.8,0)
\psdot[dotsize=3pt](1.1,0.2)
\psdot[dotsize=3pt](2,-1.6)
\psdot[dotsize=3pt](1.3,0)
\psdot[dotsize=3pt](-1.6,1.9)
\psdot[dotsize=3pt](-1.2,-1)
\psdot[dotsize=3pt](1.3,0.5)
\psdot[dotsize=3pt](1,0.6)
\psdot[dotsize=3pt](0.2,-1.6)
\psdot[dotsize=3pt](-0.6,0.2)
\psdot[dotsize=3pt](-0.8,-1)
\psdot[dotsize=3pt](1.9,0.7)
\psdot[dotsize=3pt](1.8,-1.2)
\psdot[dotsize=3pt](-1.8,-1)
\psdot[dotsize=3pt](1.4,0.8)
\psdot[dotsize=3pt](-0.6,-1.8)
\psdot[dotsize=3pt](1.1,0.3)
\psdot[dotsize=3pt](0.1,-1)
\psdot[dotsize=3pt](-1.7,-1)
\psdot[dotsize=3pt](1,-0.2)
\psdot[dotsize=3pt](-0.4,-1.3)
\psdot[dotsize=3pt](-1.1,-0.2)
\psdot[dotsize=3pt](-0.1,-0.3)
\psdot[dotsize=3pt](0.9,-0.9)
\psdot[dotsize=3pt](-0.1,0.5)
\psdot[dotsize=3pt](2,1.9)
\psdot[dotsize=3pt](-1.5,-1)
\psdot[dotsize=3pt](-1.5,1.1)
\psdot[dotsize=3pt](0.6,-0.6)
\psline[linewidth=1.8pt,linecolor=green](-2.5,-1)(2.5,1)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img75647da60eefb8a2e90071729da4e9bf.png)
Przynależność i rozmieszczenie punktów w czterech ćwiartkach wykresu Morana wskazuje na rodzaj autokorelacji. Jeśli punkty rozłożone są głównie w ćwiartce drugiej (LH) i czwartej (HL) – świadczy to o ujemnej autokorelacji, gdy należą głównie do ćwiartki pierwszej (HH) i trzeciej (LL) – świadczy to o autokorelacji dodatniej. Gdy punkty rozkładają się równomiernie we wszystkich czterech ćwiartkach, wówczas autokorelacja przestrzenna nie istnieje.
Na wykresie Morana rysowana jest też linia regresji, której kierunek również pozwala na interpretację współczynnika Morana 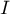 :
:
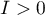 oznacza występowanie klasterów podobnych wartości – dodatnią autokorelację, tj. punkty pomiarowe leżą blisko linii prostej a wzrostowi zmiennej
oznacza występowanie klasterów podobnych wartości – dodatnią autokorelację, tj. punkty pomiarowe leżą blisko linii prostej a wzrostowi zmiennej 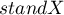 odpowiada wzrost zmiennej
odpowiada wzrost zmiennej 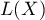 ;
;
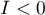 oznacza występowanie tzw. hot spots czyli zdecydowanie różnych wartości w obszarach sąsiedzkich – ujemną autokorelację, tj. punkty pomiarowe leżą blisko linii prostej, lecz wzrostowi zmiennej
oznacza występowanie tzw. hot spots czyli zdecydowanie różnych wartości w obszarach sąsiedzkich – ujemną autokorelację, tj. punkty pomiarowe leżą blisko linii prostej, lecz wzrostowi zmiennej 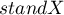 odpowiada spadek
odpowiada spadek 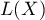 ;
;
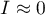 oznacza losowe rozłożenie się badanej wartości w przestrzeni – brak autokorelacji, tj. uzyskany rozkład przestrzenny jest tak samo prawdopodobny jak każdy inny rozkład.
oznacza losowe rozłożenie się badanej wartości w przestrzeni – brak autokorelacji, tj. uzyskany rozkład przestrzenny jest tak samo prawdopodobny jak każdy inny rozkład.
Kwadrat współczynnika Morana 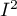 informuje o stopniu (jest to procent), w jakim wartość zmiennej w obiekcie
informuje o stopniu (jest to procent), w jakim wartość zmiennej w obiekcie  jest tłumaczona przez wartość tej zmiennej w obiektach sąsiednich.
jest tłumaczona przez wartość tej zmiennej w obiektach sąsiednich.
Uwaga!
Gdy wartości badanej cechy charakteryzuje duża zmienność wariancji, wówczas pożądane jest jej ustabilizowanie. Podstawowe informacje na temat wygładzania zmiennych zostały opisane w rozdziale Wygładzanie przestrzenne zmiennej
Istotność współczynnika autokorelacji Morana
Test do sprawdzania istotności współczynnika autokorelacji Morana służy do weryfikacji hipotezy o braku autokorelacji pomiędzy 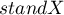 a opóźnieniem przestrzennym
a opóźnieniem przestrzennym 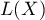 .
.
Hipotezy:
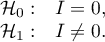
Statystyka testowa ma postać:
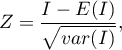
gdzie:
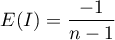 – wartość oczekiwana,
– wartość oczekiwana,
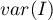 – wariancja.
– wariancja.
W zależności od założenia dotyczącego rozkładu populacji, z której pochodzi próba, wybierany jest sposób wyznaczania wariancji (Cliff i Ord (1981)2), oraz Goodchild (1986)3)).
Jeśli jest to rozkład normalny, wówczas:
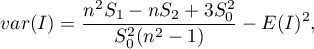
gdzie:
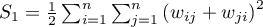 ,
,
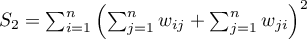 .
.
Jeśli rozkład jest losowy, wówczas:
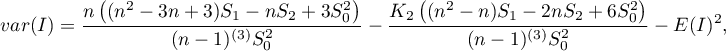
gdzie:
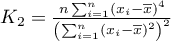 ,
,
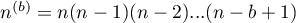 .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wartość  , wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności
, wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności  :
:

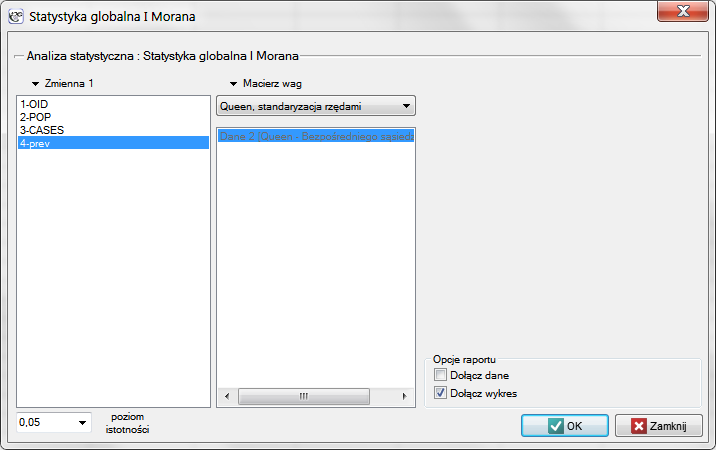
Okno z ustawieniami opcji analizy Morana wywołujemy poprzez menu Analiza przestrzenna → Statystyki przestrzenne → Statystyka globalna I Morana.
Przykład (katalog: leukemia, plik: leukemia.pqs)
Analizie poddamy dane zebrane i przeanalizowane przez L.A. Wallera i innych w roku 19924) i 19945), opisane na 281 obiektach w roku 20046).
- Mapa
leukemiazawiera informacje o lokalizacji 281 wielokątów (regionów spisowych (ang.census tracts)) w północnej części stanu New York. Mapa została przygotowana w układzie współrzędnych prostokątnych płaskich UTM 18N, i bazuje na danych pliku BNA (Boundary File) dostępnego na serwerze CIESIN ftp.ciesin.columbia.edu
- Dane do mapy
leukemia:- Kolumna
CASES– liczba przypadków białaczki w latach 1978-1982 przypisana do poszczególnych obiektów (regionów spisowych). Wartość ta powinna być liczbą całkowitą, tu jednak, zgodnie z opisem Wallera (1994) część przypadków, która nie mogła zostać obiektywnie przypisana do konkretnego regionu, została podzielona proporcjonalnie. Stąd liczności przypadków przypisanych do 281 obiektów nie są liczbami całkowitymi. - Kolumna
POP– liczność populacji w poszczególnych obiektach. - Kolumna
prev– współczynnik częstości występowania białaczki na 100000 osób, dla każdego obiektu w jednym roku: prev=(CASES/POP)*100000/5
Interesujące z epidemiologicznego punktu widzenia są regiony, gdzie częstość występowania białaczki jest wyższa. Ich zgrupowanie bowiem, mogłoby wskazywać na istnienie w ich obrębie teratogenów środowiskowych, będących przyczyną zwiększonej częstości występowania białaczki.
Zaczynamy od przedstawienia rozkładu geograficznego współczynnika częstości (prev) na mapie. W tym celu wyrysowujemy mapę w Menadżerze Map i edytujemy warstwę  wybierając
wybierając Stopniowanie kolorów:
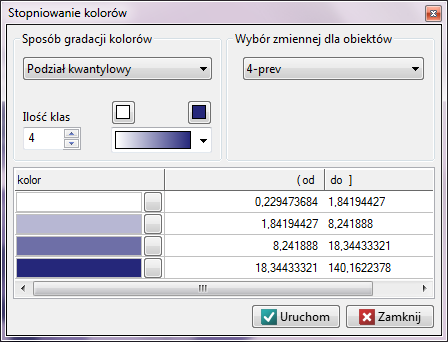
Mamy do dyspozycji kilka sposobów kolorowania mapy - tu wybieramy kolorowanie zgodnie z wartościami zmiennej prev dzieląc ją na kwartyle:
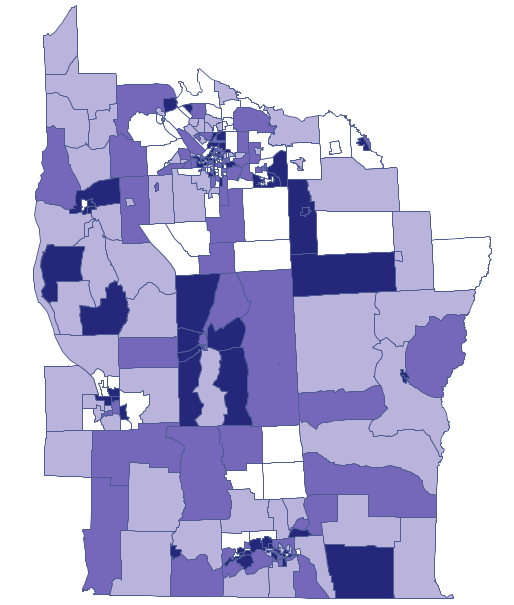
Kolory ciemne na mapie obrazują miejsca o wyższym współczynniku częstości białaczki, miejsca jasne to niski współczynnik. By dowiedzieć się, czy ich rozkład geograficzny jest losowy, czy tworzą one skupiska, wyliczymy współczynnik Morana. Przed wyliczeniem tego współczynnika należy zdecydować w jaki sposób definiowane będzie sąsiedztwo regionów i najlepiej utworzyć odpowiednią macierz wag. W oknie analizy Morana możemy wybrać dowolną macierz wygenerowaną wcześniej za pomocą menu Analiza przestrzenna → Narzędzia → Macierz wag przestrzennych lub wskazać proponowaną przez program macierz sąsiedztwa według wspólnej granicy – Queen, standaryzowaną rzędami.
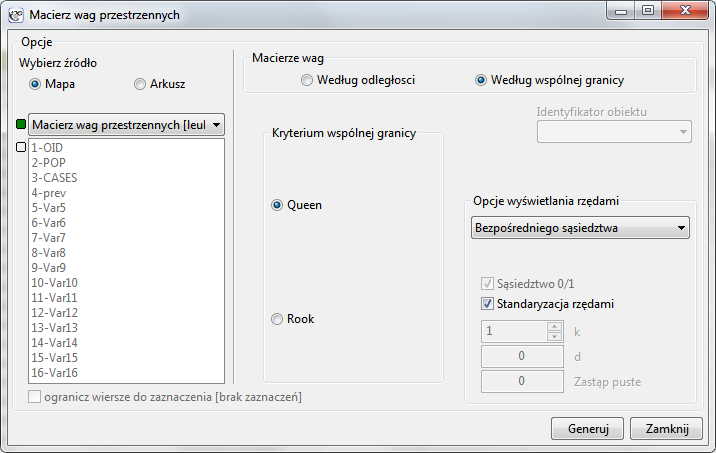
Po wygenerowaniu macierzy wag, zaznaczamy plik leukemia i przystępujemy do analizy Morana wybierając menu Analiza przestrzenna → Statystyki przestrzenne → Statystyka globalna I Morana. W oknie analizy wybieramy zmienną Prev i standaryzowaną rzędami macierz sąsiedztwa Queen, oraz zaznaczamy opcję Dołącz wykres.
Współczynnik korelacji Morana uzyskany w analizie jest niewielki i wynosi 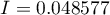 :
:
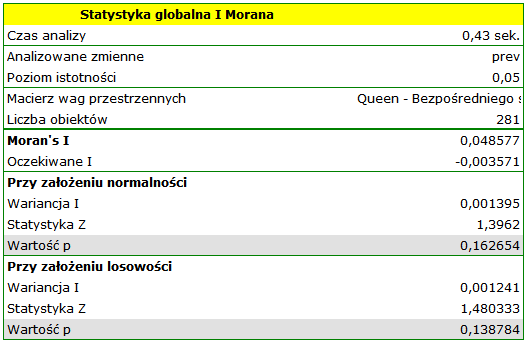
Testując istotność współczynnika Morana, badamy losowość rozkładu współczynnika częstości białaczki na badanym obszarze. Sprawdzamy, czy podobne odcienie na mapie są ulokowane blisko siebie, czy też nie. Inaczej mówiąc: sprawdzamy czy szansa zachorowania na białaczkę w badanej populacji zależy od lokalizacji geograficznej czy też nie. Wartość  wyliczona przy założeniu losowości, jak przy założeniu normalności jest większa niż standardowo przyjmowany poziom istotności 0.05, co oznacza brak dowodów na autokorelację. Przyjmujemy więc, że rozkład zmiennej
wyliczona przy założeniu losowości, jak przy założeniu normalności jest większa niż standardowo przyjmowany poziom istotności 0.05, co oznacza brak dowodów na autokorelację. Przyjmujemy więc, że rozkład zmiennej prev jest rozkładem losowym. Potwierdzeniem tego jest wykres Morana:
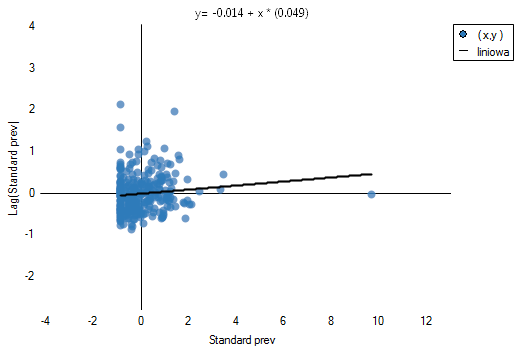
Istnienie dodatniej autokorelacji, którą jesteśmy najbardziej zainteresowani, skutkowałoby rozmieszczeniem punktów wykresu Morana w ćwiartce I i III. Tu widzimy jednak, że punkty znajdują się równie często w ćwiartce I i III jak w II i IV.
2014/08/19 15:42
· admin
Statystyka globalna Gearego
Podobnie jak analiza Morana statystyka globalna Gearego bada stopień intensywności danej cechy w obiektach przestrzennych.
Uwaga!
Nie zaleca się przeprowadzania analizy Gearego dla obiektów nie posiadających sąsiedztwa (obiektów opisanych w macierzy wag wyłącznie wartością 0). Obiekty takie można wykluczyć z analizy dezaktywując je (Rozdział Ograniczenie obszaru roboczego), lub przeprowadzić analizę wybierając inny sposób definiowania sąsiedztwa (inną macierz wag).
Współczynnik autokorelacji Gearego – wprowadzony przez Gearego w roku 19547).
Jest jedną z możliwych alternatyw dla statystyki globalnej Morana. Podobnie jak analiza Morana bada ona stopień intensywności danej cech  w obiektach przestrzennych opisanych za pomocą macierzy wag o elementach
w obiektach przestrzennych opisanych za pomocą macierzy wag o elementach 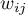 . Tym razem zamiast wyliczania sumy iloczynów :
. Tym razem zamiast wyliczania sumy iloczynów : 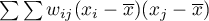 wyliczana jest suma kwadratów różnic:
wyliczana jest suma kwadratów różnic:
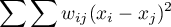
W rezultacie współczynnik autokorelacji Gearego wyraża się wzorem:
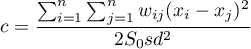
gdzie:
 – liczba obiektów przestrzennych (liczba punktów lub wielokątów),
– liczba obiektów przestrzennych (liczba punktów lub wielokątów),
 ,
, 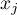 – to wartości zmiennej dla porównywanych obiektów,
– to wartości zmiennej dla porównywanych obiektów,
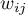 – elementy przestrzennej macierzy wag (macierz wag standaryzowana rzędami do jedynki),
– elementy przestrzennej macierzy wag (macierz wag standaryzowana rzędami do jedynki),
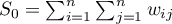 ,
,
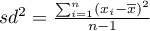 – wariancja,
– wariancja,
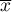 – to średnia wartość zmiennej dla wszystkich obiektów.
– to średnia wartość zmiennej dla wszystkich obiektów.
Interpretacja współczynnika Gearego:
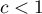 i
i 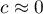 oznacza występowanie klasterów podobnych wartości – dodatnią autokorelację;
oznacza występowanie klasterów podobnych wartości – dodatnią autokorelację;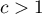 oznacza występowanie tzw. hot spots czyli zdecydowanie różnych wartości w obszarach sąsiedzkich – ujemną autokorelację;
oznacza występowanie tzw. hot spots czyli zdecydowanie różnych wartości w obszarach sąsiedzkich – ujemną autokorelację;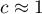 oznacza losowe rozłożenie się badanej wartości w przestrzeni – brak autokorelacji.
oznacza losowe rozłożenie się badanej wartości w przestrzeni – brak autokorelacji.
Uwaga!
Gdy wartości badanej cechy charakteryzuje duża zmienność wariancji, wówczas pożądane jest jej ustabilizowanie. Podstawowe informacje na temat wygładzania zmiennych zostały opisane w rozdziale Wygładzanie przestrzenne zmiennej
Istotności współczynnika autokorelacji Gearego
Test do sprawdzania istotności współczynnika autokorelacji Gearego służy do weryfikacji hipotezy o braku autokorelacji przestrzennej.
Hipotezy:
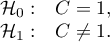
Statystyka testowa ma postać:
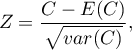
gdzie:
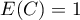 – wartość oczekiwana,
– wartość oczekiwana,
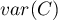 – wariancja.
– wariancja.
W zależności od założenia dotyczącego rozkładu populacji, z której pochodzi próba, wybierany jest sposób wyznaczania wariancji (Cliff i Ord (1981)8), oraz Goodchild (1986)9)). Jeśli jest to rozkład normalny, wówczas:
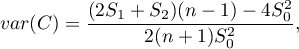
gdzie:
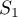 i
i 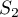 zdefiniowane są jak dla analizy Morana.
zdefiniowane są jak dla analizy Morana.
Jeśli rozkład jest losowy, wówczas:
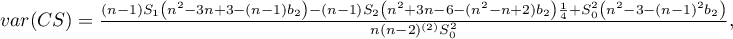
gdzie:
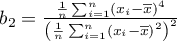 ,
,
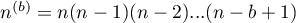 .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wartość  , wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności
, wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji analizy Gearego wywołujemy poprzez menu Analiza przestrzenna → Statystyki przestrzenne → Statystyka globalna C Gearego.
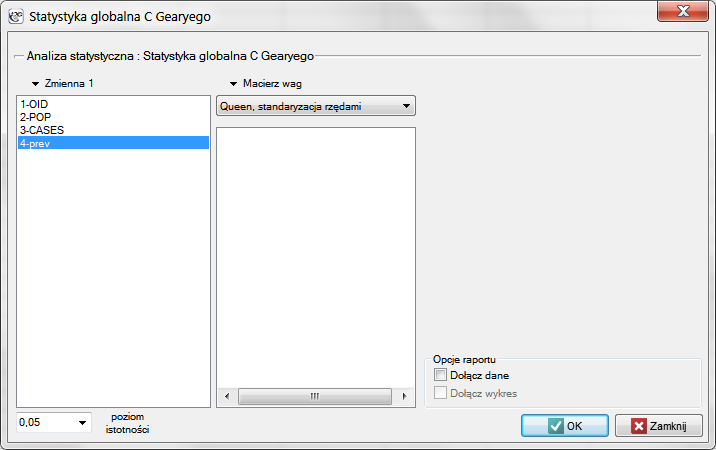
Przykład c.d. (katalog: leukemia, plik: leukemia)
Analizie poddamy dane dotyczące białaczki.
- Mapa
leukemiazawiera informacje o lokalizacji 281 wielokątów (regionów spisowych (ang.census tracts)) w północnej części stanu New York. - Dane do mapy
leukemia:- Kolumna
CASES– liczba przypadków białaczki w latach 1978-1982 przypisana do poszczególnych obiektów (regionów spisowych). Wartość ta powinna być liczbą całkowitą, tu jednak, zgodnie z opisem Wallera (1994) część przypadków, która nie mogła zostać obiektywnie przypisana do konkretnego regionu, została podzielona proporcjonalnie. Stąd liczności przypadków przypisanych do 281 obiektów nie są liczbami całkowitymi. - Kolumna
POP– liczność populacji w poszczególnych obiektach. - Kolumna
prev– współczynnik częstości występowania białaczki na 100000 osób, dla każdego obiektu w jednym roku: prev=(CASES/POP)*100000/5
Analiza globalna Morana wskazała na brak autokorelacji przestrzennej. Tym razem, by sprawdzić, czy na badanym obszarze północnej części stanu New York możliwe jest zlokalizowanie klasterów białaczki, wyliczymy globalną statystykę C Gearego.
Zaczynamy od przedstawienia rozkładu geograficznego współczynnika częstości (prev) na mapie zgodnie z wartościami zmiennej prev dzieląc ją na kwartyle:

Kolory ciemne na mapie obrazują miejsca o wyższym współczynniku częstości białaczki, miejsca jasne to niski współczynnik. Współczynnik korelacji Gearego uzyskany w analizie wynosi: 0.884986.
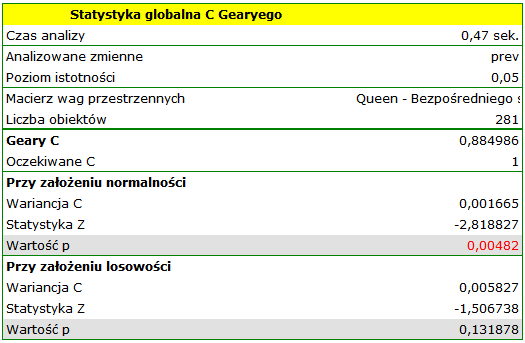
Uzyskany rezultat przy założeniu losowego rozkładu danych jest różny od wyniku uzyskanego przy założeniu rozkładu normalnego. Może to świadczyć o niestabilności wyników i być wskazaniem do dalszych analiz opartych na zmiennych wygładzonych.
2014/08/19 15:43
· admin
1)
Moran P.A.P. (1947), The Interpretation of Statistical Maps. Journal of the Royal Statistical Society, B10, 243-51
3)
Goodchild M.F (1986), Spatial Autocorrelation, CATMOG 47, Geobooks: Norwich UK
4)
Waller L.A., Turnbull B.W., Clark L.C., Nasca P. (1992), Chronic disease surveillance and testing of clustering of disease and exposure : Application to leukemia incidence and TCE-contaminated dumpsites in upstate New York. Environmetrics, 3, 281-300
5)
Waller L.A., Turnbull B.W., Clark, L.C., Nasca P. (1994), Spatial pattern analyses to detect rare disease clusters, in Case Studies in Biometry, N. Lange, et al., Editors. , John Wiley and Sons: New York, 3-23
6)
Waller L.A., Gotway C.A. (2004), Applied Spatial Statistics for Public Health Data. New York: John Wiley and Sons
7)
Geary R.C. (1954), The Contiguity Ratio and Statistical Mapping. The Incorporated Statistician, 5, 115-45
9)
Goodchild M.F. (1986), Spatial Autocorrelation, CATMOG 47, Geobooks: Norwich UK
przestrzenpl/autocorpl.txt · ostatnio zmienione: 2014/12/19 00:33 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

