Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:warstwpl
Spis treści
Analiza dla warstw
Metoda Mantela-Haenszela dla wielu tabel
Metoda Mantela-Haenszela dla tabel 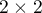 (ang. Mantel-Haenszel method for 2×2 tables) zaproponowana została przez Mantela i Haenszela (1959)1) a następnie rozszerzona przez Mantela (1963)2). Szerszy przegląd rozwoju tych metod został przeprowadzony m.in. przez Newman (2001)3).
(ang. Mantel-Haenszel method for 2×2 tables) zaproponowana została przez Mantela i Haenszela (1959)1) a następnie rozszerzona przez Mantela (1963)2). Szerszy przegląd rozwoju tych metod został przeprowadzony m.in. przez Newman (2001)3).
Metoda Mantela-Haenszela może być używana między innymi do analizy tabel 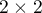 występujących w kilku (
występujących w kilku (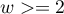 ) warstwach tworzonych przez tzw. zmienną uwikłaną (ang. confounding). Dla kolejnych warstw (
) warstwach tworzonych przez tzw. zmienną uwikłaną (ang. confounding). Dla kolejnych warstw (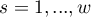 ) budowane są tabele kontyngencji
) budowane są tabele kontyngencji 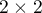 liczności obserwowanych:
liczności obserwowanych:

Okno z ustawieniami opcji metod Mantel-Haenszel OR/RR wywołujemy poprzez menu Statystyka→Analiza dla warstw→Mantel-Haenszel OR/RR.
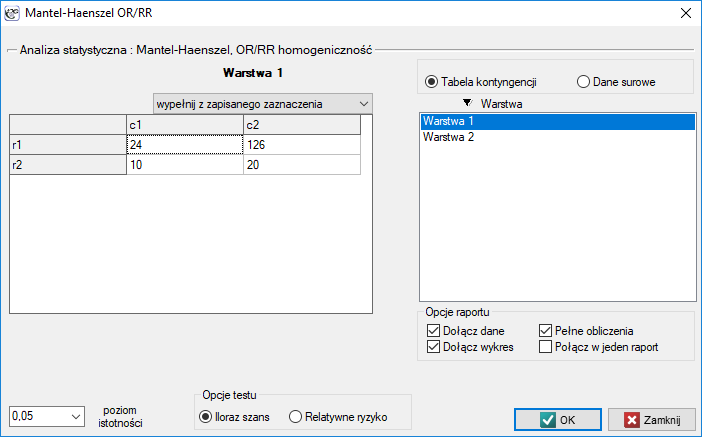
Iloraz szans Mantela-Haenszela
Jeśli wszystkie tabele (tworzone przez poszczególne warstwy) są homogeniczne (warunek ten można sprawdzić przy pomocy testu chi-kwadrat homogeniczności OR), wówczas na podstawie tych tabel można wyznaczyć wspólny iloraz szans wraz z przedziałami ufności. Taki iloraz szans jest średnią ważoną ilorazów szans wyznaczonych dla poszczególnych warstw. Zastosowanie ważonej metody zaproponowanej przez Mantela i Haenszela pozwala na uwzględnienie wkładu (wagi), jaki do budowy wspólnego ilorazu szans wnosi każda warstwa (im bardziej liczna warstwa, tym większy ma wpływ na powstały iloraz szans).
Wagi dla każdej warstwy wyznacza się zgodnie z wzorem:
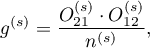
a Iloraz szans Mantela-Haenszela:
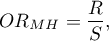
gdzie:
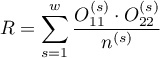 ,
,
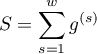 .
.
Przedział ufności dla 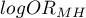 wyznacza się na podstawie błędu standardowego (RGB
wyznacza się na podstawie błędu standardowego (RGB  Robins
Robins Breslow–-Greenland4)5)) wyliczonego ze wzoru:
Breslow–-Greenland4)5)) wyliczonego ze wzoru:
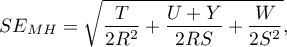
gdzie:
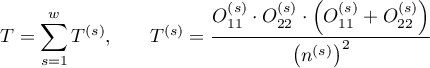 ,
,
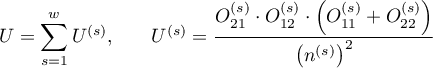 ,
,
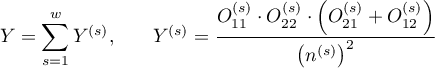 ,
,
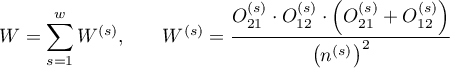 .
.
Test  Mantela-Haenszela (ang. Mantel-Haenszel Chi-square test) służy do weryfikacji hipotezy o istotności wyznaczonego ilorazu szans (
Mantela-Haenszela (ang. Mantel-Haenszel Chi-square test) służy do weryfikacji hipotezy o istotności wyznaczonego ilorazu szans (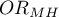 ) i powinien być wyliczany przy dużych licznościach, tzn. gdy są spełnione obydwa warunki tzw. „reguły 5”:
) i powinien być wyliczany przy dużych licznościach, tzn. gdy są spełnione obydwa warunki tzw. „reguły 5”:
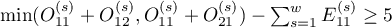 dla wszystkich warstw
dla wszystkich warstw 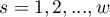 ,
,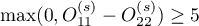 dla wszystkich warstw
dla wszystkich warstw 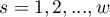 .
.
Kiedy występują wartości zerowe w tabeli stosowana jest korekta na ciągłość (powiększenie liczności o wartość o,5), zarówno dla liczności obserwowanych jak i dla liczności oczekiwanych.
Hipotezy:
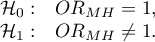
Statystyka testowa ma postać:
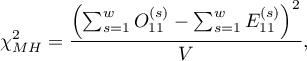
gdzie:
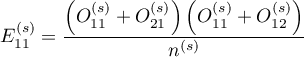 to wartości oczekiwane w pierwszej komórce tabeli kontyngencji, dla poszczególnych warstw
to wartości oczekiwane w pierwszej komórce tabeli kontyngencji, dla poszczególnych warstw 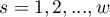 ,
,
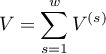 ,
,
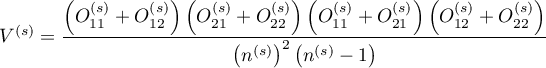 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z jednym stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Test  homogeniczności dla
homogeniczności dla 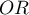 (ang. Chi-square test of homogeneity for $OR$) służy do weryfikacji hipotezy o tym, że zmienna tworząca warstwy jest efektem modyfikującym, tzn. wpływa ona na wyznaczany iloraz szans w taki sposób, że jest on znacząco inny dla poszczególnych warstw.
(ang. Chi-square test of homogeneity for $OR$) służy do weryfikacji hipotezy o tym, że zmienna tworząca warstwy jest efektem modyfikującym, tzn. wpływa ona na wyznaczany iloraz szans w taki sposób, że jest on znacząco inny dla poszczególnych warstw.
Hipotezy:
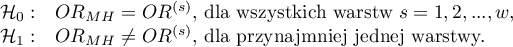
Statystyka testowa (Breslow–-Day (1980)6), Tarone (1985)7)8)) ma postać:
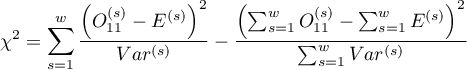
gdzie:
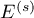 jest rozwiązaniem równania kwadratowego (solution to the quadratic equation):
jest rozwiązaniem równania kwadratowego (solution to the quadratic equation):
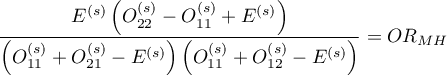 ,
,
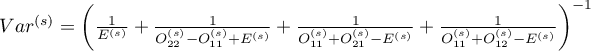 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyliczaną według wzoru: 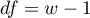 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przykład (plik leptospiroza.pqs)
Przedstawiona tabela pokazuje hipotetyczne wyniki ankiety przeprowadzonej w celu wykrycia czynników ryzyka występowania leptospirozy wśród mieszkańców miasta i wsi Zachodnich Indii (gdzie obszar wiejski traktowany jest jako czynnik narażenia)9). Występowanie przeciwciał leptospirozy jest pośrednim dowodem na obecność zakażenia.

Szansa wystąpienia przeciwciał leptospirozy mieszkańców miasta i wsi jest taka sama (OR=1). Chcemy wiedzieć, jaka będzie szansa wystąpienia przeciwciał leptospirozy, gdy w analizie weźmiemy pod uwagę również płeć. Podzielimy więc próbę na 2 warstwy ze względu na płeć (są one zapamiętane w pliku jako zaznaczony zakres):


Płeć jest powiązana z obydwoma czynnikami (z występowaniem przeciwciał leptospirozy i z miejscem zamieszkania w Zachodnich Indiach). Jest to czynnik wikłający, którego zignorowanie może prowadzić do błędnych wyników.
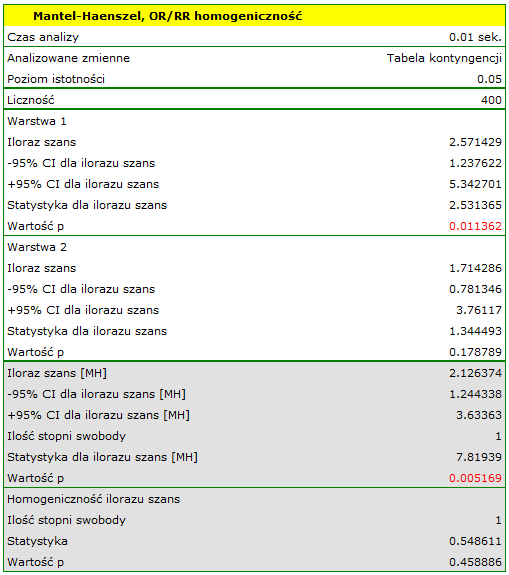
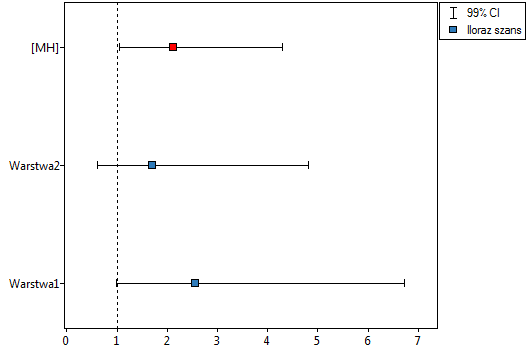
Szansa wystąpienia przeciwciał leptospirozy jest większa dla mieszkańców wsi, zarówno dla kobiet (OR[95%CI]= 2.57[1.24, 5.34]) jak i dla mężczyzn (OR[95%CI]= 1.71[0.78, 3.76]). Tabele są homogeniczne (p=0.465049). Możemy zatem posłużyć się wyliczonym ilorazem szans wspólnym dla obu tabel (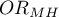 [95%CI]=2.13[1.24, 3.65]). W rezultacie uzyskany wynik wskazuje, że szansa wystąpienia przeciwciał leptospirozy jest istotnie większa dla osób zamieszkujących tereny wiejskie (p=0.005169).
[95%CI]=2.13[1.24, 3.65]). W rezultacie uzyskany wynik wskazuje, że szansa wystąpienia przeciwciał leptospirozy jest istotnie większa dla osób zamieszkujących tereny wiejskie (p=0.005169).
2014/08/22 20:00
Relatywne ryzyko Mantela-Haenszela
Jeśli wszystkie tabele (tworzone przez poszczególne warstwy) są homogeniczne (warunek ten można sprawdzić przy pomocy testu chi-kwadrat homogeniczności RR), wówczas na podstawie tych tabel można wyznaczyć wspólne relatywne ryzyko wraz z przedziałami ufności. Takie relatywne ryzyko jest średnią ważoną wartości Relatywnego Ryzyka wyznaczonego dla poszczególnych warstw. Zastosowanie ważonej metody zaproponowanej przez Mantela i Haenszela pozwala na uwzględnienie wkładu (wagi), jaki do budowy wspólnego Relatywnego Ryzyka wnosi każda warstwa (im bardziej liczna warstwa, tym większy ma wpływ na powstałe relatywne ryzyko).
Wagi dla każdej warstwy wyznacza się zgodnie z wzorem:
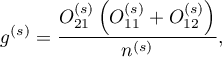
a relatywne ryzyko Mantela-Haenszela:
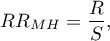
gdzie:
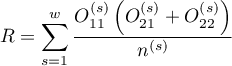 ,
,
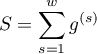 .
.
Przedział ufności dla 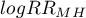 wyznacza się na podstawie błędu standardowego wyliczonego ze wzoru:
wyznacza się na podstawie błędu standardowego wyliczonego ze wzoru:
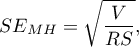
gdzie:
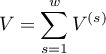 ,
,
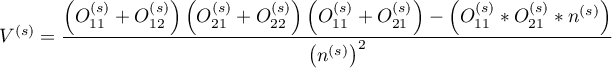 .
.
Test  Mantela-Haenszela (ang. Mantel-Haenszel Chi-square test) służy do weryfikacji hipotezy o istotności wyznaczonego Relatywnego Ryzyka (
Mantela-Haenszela (ang. Mantel-Haenszel Chi-square test) służy do weryfikacji hipotezy o istotności wyznaczonego Relatywnego Ryzyka (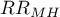 ) i powinien być wyliczany przy dużych licznościach w tabeli kontyngencji.
) i powinien być wyliczany przy dużych licznościach w tabeli kontyngencji.
Hipotezy:
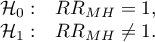
Statystyka testowa ma postać:
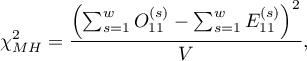
gdzie:
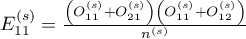 to wartości oczekiwane w pierwszej komórce tabeli kontyngencji, dla poszczególnych warstw
to wartości oczekiwane w pierwszej komórce tabeli kontyngencji, dla poszczególnych warstw 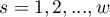 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z jednym stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Test  homogeniczności dla
homogeniczności dla 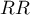 (ang. Chi-square test of homogeneity for RR) służy do weryfikacji hipotezy o tym, że zmienna tworząca warstwy jest efektem modyfikującym, tzn. wpływa ona na wyznaczane relatywne ryzyko w taki sposób, że jest on znacząco inne dla poszczególnych warstw.
(ang. Chi-square test of homogeneity for RR) służy do weryfikacji hipotezy o tym, że zmienna tworząca warstwy jest efektem modyfikującym, tzn. wpływa ona na wyznaczane relatywne ryzyko w taki sposób, że jest on znacząco inne dla poszczególnych warstw.
Hipotezy:
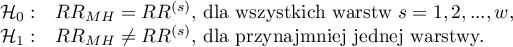
Statystyka testowa oparta o ważoną metodę najmniejszych kwadratów ma postać:
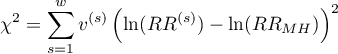
gdzie:
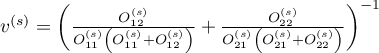 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyliczaną według wzoru: 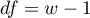 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

2014/08/22 20:00
2014/08/22 20:00
1)
Mantel N. and Haenszel W. (1959), Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22,719-748
2)
Mantel N. (1963), Chi-square tests with one degree of freedom: Extensions of the Mantel-Haenszel procedure. J. Am. Statist. Assoc., 58, 690-700
3)
Newman S.C.(2001), Biostatistical Methods in Epidemiology. 2nd ed. New York: John Wiley
4)
Robins, J., Breslow, N., and Greenland S. (1986), Estimators of the Mantel–Haenszel variance consistent in both sparse data and large-strata limiting models. Biometrics 42, 311–323
5)
Robins, J., Greenland S. and Breslow, N.E. (1986), A general estimator for the variance of the Mantel–Haenszel odds ratio. American Journal of Epidemiology 124, 719–723
6)
Breslow N.E., Day N.E. (1980), Statistical Methods in Cancer Research: Vol. I - The Analysis of Case-Control Studies. Lyon: International Agency for Research on Cancer
7)
Breslow N.E. (1996), Statistics in epidemiology: the case-control study', Journal of the American Statistical Association, 91, 14-28
8)
Tarone R.E. (1985), On heterogeneity tests based on efficient scores. Biometrika 72, 91–95
9)
Betty R. Kirkwood and Jonathan A. C. Sterne (2003), Medical Statistics (2nd ed.). Meassachusetts: Blackwell Science, 177-188, 240-248
statpqpl/warstwpl.txt · ostatnio zmienione: 2019/12/17 17:29 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

