Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown2grpl:nparpl:rr_orpl
Relatywne Ryzyko i Iloraz Szans
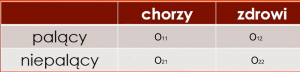
Określenie Szansy lub Ryzyka wystąpienia badanego zjawiska na podstawie narażenia na czynnik mogący je wywoływać szacujemy na podstawie danych zebranych w tabeli kontyngencji  . Na przykład możemy sprawdzać jak palenie papierosów wpływa na zachorowanie:
. Na przykład możemy sprawdzać jak palenie papierosów wpływa na zachorowanie:
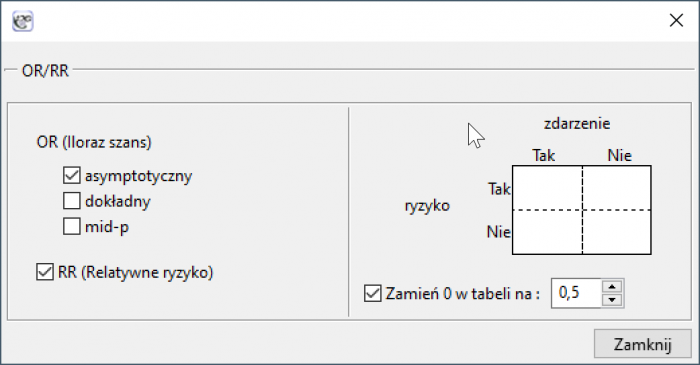
Okno z możliwością wyznaczenia tych miar wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher, OR/RR wybierając OR/RR… lub poprzez ''Kreator''.
Jeśli przeprowadzone badanie jest badaniem typu przypadek-kontrola, wówczas dla takiej tabeli wylicza się Iloraz Szans na to, że badane zjawisko wystąpi. Zwykle są to badania retrospektywne - czyli takie, w których badacz sam decyduje o wielkości próby, w której badane zjawisko występuje i próby kontrolnej, wolnej od tego zjawiska.
Jeśli natomiast badanie jest badaniem kohortowym, wówczas dla takiej tabeli wylicza się Relatywne Ryzyko na to, że badane zjawisko wystąpi. Zwykle są to badania prospektywne - czyli takie, w których badacz dba o to, by warunki eksperymentu pozwalały na to by struktura występowania badanego zjawiska w próbie była zbliżona do struktury tego zjawiska w populacji.
Dla wyznaczenia Ilorazu Szans (ang. Odds Ratio - OR) wylicza się szansę bycia przypadkiem w grupie narażonej na czynnik ryzyka i szansę bycia przypadkiem w grupie nie narażonej na czynnik ryzyka zgodnie z wzorami:
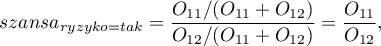

Iloraz Szans to:
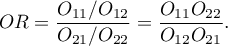
- Test do sprawdzenia istotności OR
Test ten służy do weryfikacji hipotezy o tym, że szansa na wystąpienie badanego zjawiska jest taka sama w grupie narażonej i w grupie nienarażonej na czynnik ryzyka.
Hipotezy:
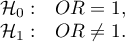
Statystyka testowa wyraża się wzorem:
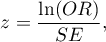
gdzie:
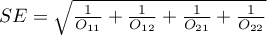 - błąd standardowy logarytmu Ilorazu Szans.
- błąd standardowy logarytmu Ilorazu Szans.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Często w interpretacji istotności Ilorazu Szans posługujemy się wyznaczonym dla niego przedziałem ufności. Badamy wówczas, czy przedział ten zawiera wartość 1.
Dla badania kohortowego można wyznaczać Ryzyko wystąpienia badanego zjawiska (ponieważ próbka powinna zbliżać się strukturą zjawiska, które interesuje badacza do populacji, z której została pobrana) oraz wyliczać Relatywne Ryzyko (ang. Relative Risk - RR).
Oszacowane Ryzyko wystąpienia badanego zjawiska wyraża się wzorem:
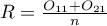
natomiast Relatywne Ryzyko:
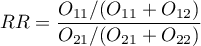
- Test do sprawdzenia istotności RR
Test ten służy do weryfikacji hipotezy o tym, że ryzyko wystąpienia badanego zjawiska jest takie samo w grupie narażonej i w grupie nienarażonej na czynnik ryzyka.
Hipotezy:
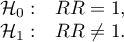
Statystyka testowa wyraża się wzorem:
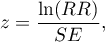
gdzie:
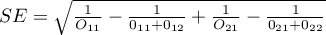 - błąd standardowy logarytmu Relatywnego Ryzyka.
- błąd standardowy logarytmu Relatywnego Ryzyka.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Często w interpretacji istotności Relatywnego Ryzyka posługujemy się wyznaczonym dla niego przedziałem ufności. Badamy wówczas, czy przedział ten zawiera wartość 1.
Uwaga!
Gdy w tabeli danych znajdują się zera, wówczas wyliczenie ilorazu szans lub relatywnego ryzyka może być niemożliwe. W takiej sytuacji, aby zagwarantować możliwość wyznaczenia ilorazu szans, w oknie analizy można zaznaczyć opcję Zamień 0 w tabeli na:. Wybór tej opcji (korekty na ciągłość) powoduje dodanie do wszystkich komórek tabeli zadanej wartości.
statpqpl/porown2grpl/nparpl/rr_orpl.txt · ostatnio zmienione: 2020/10/06 14:04 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


 )
)
