Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:redpl
Spis treści
Redukcja wymiarów i grupowanie
Wraz ze wzrostem ilości zmiennych poddawanych analizie statystycznej rośnie ich dokładność, ale rośnie też stopień komplikacji i trudności w interpretacji uzyskanych wyników. Zbyt duża ilość zmiennych niesie za sobą ryzyko wzajemnej ich korelacji. A więc informacja wnoszona przez niektóre zmienne może być redundantna, tzn. część zmiennych może nie wnosić nowej informacji do analizy, ale powtarzać informacje wniesione już przez inne zmienne. Potrzeba redukcji wymiarowości (redukcji ilości zmiennych) zrodziła całą grupę analiz poświęconej tej kwestii takich jak: analiza czynnikowa, analiza składowych głównych, analiza skupień, czy analiza dyskryminacyjna. Metody te pozwalają na wykrywanie powiązań między zmiennymi. Na podstawie tych powiązań można wyodrębnić grupy podobnych zmiennych, a do dalszych analiz wybrać tylko jednego przedstawiciela każdej grupy (jedną zmienną), albo nową zmienną której wartości są wyliczane w oparciu o pozostałe zmienne w grupie. W ten sposób mamy pewność, że informacje niesione przez każdą grupę są w analizie uwzględnione. Przy niewielkiej utracie informacji możemy więc zbiór  zmiennych zredukować do zbioru
zmiennych zredukować do zbioru  zmiennych gdzie
zmiennych gdzie 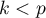
Podobnie jak grupowaniem zmiennych możemy być zainteresowani grupowaniem obiektów. Mając do dyspozycji informację o pewnych cechach obiektów jesteśmy często w stanie wyodrębnić grupy obiektów podobnych pod względem tych cech np. na podstawie informacji o kwotach przeznaczanych przez klientów pewnej sieci sklepów na poszczególne artykuły , można dokonać podziału klientów w ten sposób, by wyodrębnić segmenty klientów o podobnych preferencjach zakupowych. W konsekwencji, swoją ofertę/reklamę można przygotować nie dla ogółu kupujących, ale oddzielnie dla każdego segmentu, tak by precyzyjniej trafić w potrzeby potencjalnego klienta.
Analiza składowych głównych
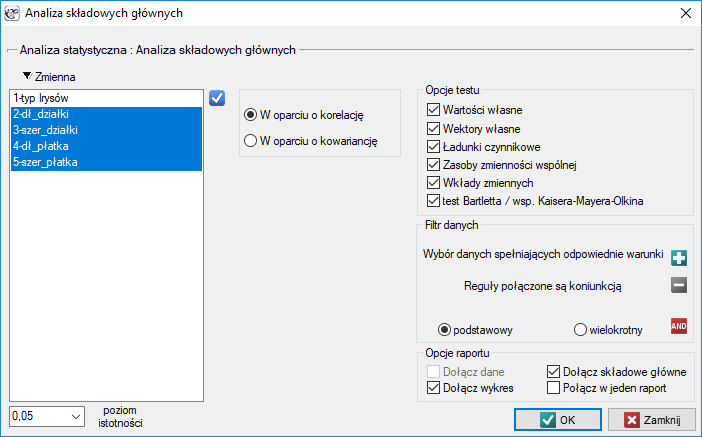
Okno z ustawieniami opcji Analizy składowych głównych wywołujemy poprzez menu Statystyki → Modele wielowymiarowe → Analiza składowych głównych.
Analiza składowych głównych polega na wyznaczeniu zupełnie nowych zmiennych (składowych głównych) będących kombinacją liniową zmiennych obserwowanych (pierwotnych). Dokładna analiza składowych głównych umożliwia wskazanie tych zmiennych pierwotnych, które mają duży wpływ na wygląd poszczególnych składowych głównych czyli tych, które tworzą grupę jednorodną. Składowa główna jest wówczas reprezentantem tej grupy. Kolejne składowe są wzajemnie ortogonalne (nieskorelowane) a ich liczba ( ) jest mniejsza lub równa liczbie zmiennych pierwotnych (
) jest mniejsza lub równa liczbie zmiennych pierwotnych ( ).
).
Poszczególne składowe główne są kombinacją liniową zmiennych pierwotnych:
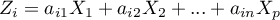 gdzie:
gdzie:
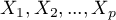 – zmienne pierwotne,
– zmienne pierwotne,
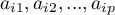 – współczynniki
– współczynniki  -tej składowej głównej
-tej składowej głównej
Każda składowa główna wyjaśnia pewną część zmienności zmiennych pierwotnych. W naturalny sposób opiera się więc na takich miarach zmienności jak kowariancja (gdy zmienne pierwotne są podobnej wielkości i są wyrażone w tych samych jednostkach) lub korelacja (gdy założenia potrzebne do stosowana kowariancji nie są spełnione).
Obliczenia matematyczne pozwalające wyodrębnić składowe główne sprowadzają się do wyznaczenia wartości własnych i odpowiadających im wektorów własnych z równania macierzowego postaci:
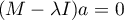 gdzie:
gdzie:
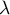 – wartości własne,
– wartości własne,
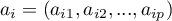 – wektor własny odpowiadający
– wektor własny odpowiadający  -tej wartości własnej,
-tej wartości własnej,
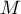 – macierz wariancji lub kowariancji zmiennych pierwotnych
– macierz wariancji lub kowariancji zmiennych pierwotnych 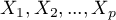 ,
,
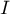 – macierz identycznościowa (1 na głównej przekątnej, 0 poza nią).
– macierz identycznościowa (1 na głównej przekątnej, 0 poza nią).
Przykład c.d. (plik: iris.pqs)
Interpretacja współczynników związanych z analizą
Każda składowa główna opisana jest poprzez:
Wartość własną
Wartość własna daje informacje o tym, jaka część całkowitej zmienności jest tłumaczona przez daną składową główną. Pierwsza składowa główna tłumaczy największą część wariancji, druga składowa tłumaczy największą część tej wariancji, która nie została wytłumaczona przez poprzednią składową, kolejna składowa tłumaczy największą część tej wariancji, która nie została wytłumaczona przez poprzednie składowe. W rezultacie każda kolejna składowa główna tłumaczy coraz mniejszą część wariancji, czyli kolejne wartości własne są coraz mniejsze.
Całkowita wariancja jest sumą wartości własnych, co pozwala, dla każdej składowej wyliczyć procent zmienności przez nią definiowany
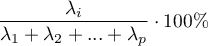
W rezultacie dla kolejnych składowych można wyliczyć również, skumulowaną zmienność i skumulowany procent zmienności.
Wektor własny
Wektor własny odzwierciedla wpływ poszczególnych zmiennych pierwotnych na daną składową główną. Zawiera współczynniki 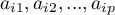 kombinacji liniowej wyznaczającej składową. Przy czym znak tych współczynników wskazuje kierunek wpływu i jest przypadkowy co nie zmienia wartości niesionej informacji.
kombinacji liniowej wyznaczającej składową. Przy czym znak tych współczynników wskazuje kierunek wpływu i jest przypadkowy co nie zmienia wartości niesionej informacji.
Ładunki czynnikowe
Ładunki czynnikowe, podobnie jak współczynniki zawarte w wektorze własnym, odzwierciedlają wpływ poszczególnych zmiennych na daną składową główną. Są to wartości obrazujące jaką część wariancji danej składowej stanowi zmienne pierwotne. Gdy analiza oparta jest na macierzy korelacji wartości te interpretujemy jako współczynniki korelacji pomiędzy zmiennymi pierwotnymi a daną składową główną.
Wkłady zmiennych
Bazują na współczynnikach determinacji pomiędzy zmiennymi pierwotnymi a daną składową główną. Wskazują jaki procent zmienności danej składowej głównej może być tłumaczony zmiennością poszczególnych zmiennych pierwotnych.
Zasoby zmienności wspólnej
Bazują na współczynnikach determinacji pomiędzy zmiennymi pierwotnymi a daną składową główną. Wskazują jaki procent zmienności danej zmiennej pierwotnej może być tłumaczony zmiennością pierwszych kilku składowych głównych. Na przykład: wynik dotyczący drugiej zmiennej zawarty w kolumnie dotyczącej czwartej składowej głównej mówi o tym, jaki procent zmienności drugiej zmiennej może być tłumaczony zmiennością pierwszych czterech składowych głównych.
Przykład c.d. (plik: iris.pqs)
2014/08/22 20:00
Interpretacja graficzna
Wiele informacji, które niosą współczynniki zwracane w tabelach można przedstawić na jednym wykresie. Umiejętność czytania wykresów pozwala na szybką interpretację wielu aspektów przeprowadzonej analizy. Wykresy zbierają w jednym miejscu informację dotyczącą wzajemnych relacji pomiędzy składowymi, zmiennymi pierwotnymi i przypadkami. Dają całościowy obraz analizy składowych głównych, przez co są bardzo dobrym jej podsumowaniem.
Wykres ładunków czynnikowych
Wykres przedstawia wektory połączone z początkiem układu współrzędnych, które to reprezentują zmienne pierwotne. Wektory te są umieszczone na płaszczyźnie wyznaczonej przez dwie wybrane składowe główne.
{3}
\psline{->}(0,0)(2.5,1)
\rput(2.5,0.8){A}
\psline{->}(0,0)(2.7,1.3)
\rput(2.4,1.43){B}
\psline{->}(0,0)(1,1)
\rput(0.7,1){C}
\psline{->}(0,0)(-1.5,0.3)
\rput(-1.4,0.5){D}
\psline{->}(0,0)(-2,-2)
\rput(-2,-1.7){E}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imga791b18820caf03e86415963084a97c1.png)
- Współrzędne końca wektora to odpowiadające im ładunki czynnikowe zmiennych.
- Długość wektora reprezentuje zasób informacyjny zmiennej pierwotnej, jaki niosą składowe główne wyznaczające układ współrzędnych. Im dłuższy wektor, tym wkład zmiennej pierwotnej w budowę składowych większy. W przypadku analizy opartej na macierzy korelacji ładunki są korelacjami pomiędzy zmiennymi pierwotnymi a składowymi, wówczas punkty wpadają do koła jednostkowego. Dzieje się tak dlatego, że współczynnik korelacji nie może przekroczyć jedynki. W rezultacie, im dana zmienna pierwotna leży bliżej brzegu tego koła, tym lepsza jest jej reprezentacja przez przedstawione główne składowe.
- Znak współrzędnych końca wektora czyli znak ładunku czynnikowego - wskazuje na dodatnią lub ujemną korelację zmiennej pierwotnej i składowych głównych tworzących układ współrzędnych. Jeżeli rozpatrujemy łącznie obie osie (2 składowe), wówczas zmienne pierwotne mogą być kwalifikowane do jednej z czterech kategorii, zależnie od kombinacji znaków (
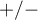 ) ich ładunków czynnikowych.
) ich ładunków czynnikowych.
- Kąt między wektorami wskazuje na skorelowanie zmiennych pierwotnych:
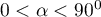 : im kąt pomiędzy wektorami reprezentującymi zmienne pierwotne jest mniejszy tym silniejsza jest dodatnia korelacja pomiędzy tymi zmiennymi.
: im kąt pomiędzy wektorami reprezentującymi zmienne pierwotne jest mniejszy tym silniejsza jest dodatnia korelacja pomiędzy tymi zmiennymi.
 - wektory te są prostopadłe, czyli zmienne pierwotne nie są skorelowane.
- wektory te są prostopadłe, czyli zmienne pierwotne nie są skorelowane.
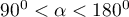 - im kąt pomiędzy wektorami reprezentującymi zmienne pierwotne jest większy, tym silniejsza jest ujemna korelacja pomiędzy tymi zmiennymi.
- im kąt pomiędzy wektorami reprezentującymi zmienne pierwotne jest większy, tym silniejsza jest ujemna korelacja pomiędzy tymi zmiennymi.
Biplot
Wykres przedstawia 2 serie danych umieszczone w układzie współrzędnych wyznaczonych przez 2 składowe główne. Serię pierwszą na wykresie stanowią dane z wykresu pierwszego (czyli wektory zmiennych pierwotnych) a serię drugą punkty przedstawiające poszczególne przypadki.

\psdot[dotsize=3pt](0.8,0)
\psdot[dotsize=3pt](1.1,0.2)
\psdot[dotsize=3pt](2,-1.6)
\psdot[dotsize=3pt](1.3,0)
\psdot[dotsize=3pt](-1.6,1.9)
\psdot[dotsize=3pt](-1.2,-1)
\psdot[dotsize=3pt](1.3,0.5)
\psdot[dotsize=3pt](1,0.6)
\psdot[dotsize=3pt](0.2,-1.6)
\psdot[dotsize=3pt](-0.6,0.2)
\psdot[dotsize=3pt](-0.8,-1)
\psdot[dotsize=3pt](1.9,0.7)
\psdot[dotsize=3pt](1.8,-1.2)
\psdot[dotsize=3pt](-1.8,-1)
\psdot[dotsize=3pt](1.4,0.8)
\psdot[dotsize=3pt](-0.6,-1.8)
\psdot[dotsize=3pt](1.1,0.3)
\psdot[dotsize=3pt](0.1,-1)
\psdot[dotsize=3pt](-1.7,-1)
\psdot[dotsize=3pt](1,-0.2)
\psdot[dotsize=3pt](-0.4,-1.3)
\psdot[dotsize=3pt](-1.1,-0.2)
\psdot[dotsize=3pt](-0.1,-0.3)
\psdot[dotsize=3pt](0.9,-0.9)
\psdot[dotsize=3pt](-0.1,0.5)
\psdot[dotsize=3pt](2,1.9)
\psdot[dotsize=3pt](-1.5,-1)
\psdot[dotsize=3pt](-1.5,1.1)
\psdot[dotsize=3pt](0.6,-0.6)
\psline{->}(0,0)(2.5,1)
\rput(2.5,0.8){A}
\psline{->}(0,0)(2.7,1.3)
\rput(2.4,1.43){B}
\psline{->}(0,0)(1,1)
\rput(0.7,1){C}
\psline{->}(0,0)(-1.5,0.3)
\rput(-1.4,0.5){D}
\psline{->}(0,0)(-2,-2)
\rput(-2,-1.7){E}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img2b39b527c98bf4a4b17471e1b7b9c745.png)
- Współrzędne punktów powinny być interpretowane jak wartości zestandaryzowane, tzn. współrzędne dodatnie wskazują na wartość wyższą od średniej wartości składowej głównej, ujemne na wartość niższą a im wyższa wartość bezwzględna tym dalej punkty znajdują się od średniej. Przy czym, jeśli na wykresie znajdują się obserwacje nietypowe - odstające, to mogą one zaburzać analizę i powinny być usunięte a analiza przeprowadzona ponownie.
- Odległości między punktami wskazują na podobieństwo przypadków - im bliżej (w znaczeniu odległości euklidesowej) zlokalizowane są względem siebie punkty, tym bardziej podobne informacje niosą porównywane przypadki.
- Rzuty prostopadłe punktów na wektory interpretujemy tak samo jak współrzędne punktów, czyli rzuty na osie z tym, że interpretacja dotyczy nie składowych głównych a zmiennych pierwotnych. Wartości umieszczone po stronie końca wektora są większe od średniej wartości zmiennej pierwotnej a wartości umieszczone na przedłużeniu wektora ale w kierunku przeciwnym są wartościami mniejszymi od średniej.
Przykład c.d. (plik: iris.pqs)
2014/08/22 20:00
Kryteria redukcji wymiarów
Nie istnieje jedno uniwersalne kryterium wyboru ilości składowych głównych. Dobrze jest wiec, aby przy wyborze kierować się kilkoma metodami. Procent wyjaśnionej wariancji
Liczba składowych głównych, jaką badacz powinien przyjąć zależy od tego, w jaki stopniu reprezentują one zmienne pierwotne, czyli zawartej w nich wariancji zmiennych pierwotnych. Wszystkie składowe główne niosą 100\% wariancji zmiennych pierwotnych. Jeśli suma wariancji dla kilku pierwszych składowych stanowi znaczną część całkowitej wariancji zmiennych pierwotnych, wówczas te składowe główne mogą w zadowalającym stopniu zastąpić zmienne pierwotne. Przyjmuje się, że wariancja ta powinna zostać odzwierciedlona w składowych głównych w ponad 80 procentach.
Kryterium Kaisera
Kryterium Kaisera mówi o tym, że składowe główne, które chcemy pozostawić do interpretacji powinny mieć przynajmniej taką samą wariancję jak dowolna wystandaryzowana zmienna pierwotna. W związku z tym, że wariancja każdej wystandaryzowanej zmiennej pierwotnej wynosi 1, to według kryterium Kaisera ważne są tylko składowe główne, których wartość własna przekracza lub jest bliska wartości 1.
Wykres osypiska
Na wykresie tym przedstawione jest tempo spadku wartości własnych, czyli procentu wyjaśnionej wariancji.

\psline{-}(1,3.4)(2,1.9)
\psdot[dotsize=3pt](2,1.9)
\psline{-}(2,1.9)(3,1.7)
\psdot[dotsize=3pt](3,1.7)
\psline{-}(3,1.7)(4,0.5)
\psdot[dotsize=3pt](4,0.5)
\psline{-}(4,0.5)(5,0.4)
\psdot[dotsize=3pt](5,0.4)
\psline{-}(5,0.4)(6,0.3)
\psdot[dotsize=3pt](6,0.3)
\psline{-}(6,0.3)(7,0.22)
\psdot[dotsize=3pt](7,0.22)
\psline{-}(7,0.22)(8,0.15)
\psdot[dotsize=3pt](8,0.15)
\psline{-}(8,0.15)(9,0.11)
\psdot[dotsize=3pt](9,0.11)
\pscircle(4,0.5){0.15}
\psline[linestyle=dotted]{->}(6,2)(4.1,0.7)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img18bff880d255fad7296e139e6e4e08a9.png)
Moment na wykresie, w którym proces ten stabilizuje się i linia malejąca przechodzi w poziomą to tzw. koniec osypiska (koniec osypywania się informacji o zmiennych pierwotnych, jaką niosą składowe główne). Składowe znajdujące się na prawo od punktu kończącego osypisko reprezentują znikomą wariancję i przedstawiają w większości losowy szum.
Przykład c.d. (plik: iris.pqs)
2014/08/22 20:00
Wyznaczenie składowych głównych
Gdy zdecydujemy ilu składowych głównych będziemy potrzebować, możemy przystąpić do ich wygenerowania. W przypadku składowych głównych powstałych w oparciu o macierz korelacji składowe główne są wyliczane jako kombinacja liniowa wystandaryzowanych zmiennych pierwotnych. Jeśli natomiast składowe główne powstały w oparciu o macierz kowariancji, wówczas są wyliczane jako kombinacja liniowa wycentrowanych względem średniej zmiennych pierwotnych.
Otrzymane w ten sposób składowe główne stanowią nowe zmienne o pewnych zaletach. Przede wszystkim zmienne te nie są współliniowe. Zwykle jest ich mniej niż zmiennych pierwotnych, czasem znacznie mniej, a niosą one tyle samo lub nieznacznie mniej informacji niż zmienne pierwotne. Są więc zmiennymi, które z powodzeniem mogą być wykorzystane w większości analiz wielowymiarowych.
Przykład c.d. (plik: iris.pqs)
2014/08/22 20:00
Zasadność stosowania Analizy składowych głównych
Jeśli zmienne nie są skorelowane (współczynnik korelacji Pearsona jest bliski 0), to wówczas przeprowadzanie analizy składowych głównych nie ma sensu. W takiej sytuacji bowiem każda zmienna stanowi już odrębną składową.
Test Bartletta
Test ten wykorzystywany jest do weryfikacji hipotezy o tym, że współczynniki korelacji pomiędzy zmiennymi są zerowe (czyli macierz korelacji jest macierzą jednostkową).
Hipotezy:
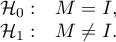
gdzie:
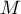 – macierz wariancji lub kowariancji zmiennych pierwotnych
– macierz wariancji lub kowariancji zmiennych pierwotnych 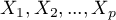 ,
,
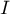 – macierz jednostkowa (1 na głównej przekątnej, 0 poza nią).
– macierz jednostkowa (1 na głównej przekątnej, 0 poza nią).
Statystyka testowa ma postać:
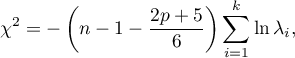
gdzie:
 – liczba zmiennych pierwotnych,
– liczba zmiennych pierwotnych,
 – liczność (liczba przypadków),
– liczność (liczba przypadków),
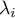 –
–  -ta wartość własna.
-ta wartość własna.
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z 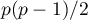 stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Współczynnik Kaisera-Mayera-Olkina
Współczynnik ten wykorzystywany jest do sprawdzania stopnia skorelowania zmiennych pierwotnych, czyli siły dowodów świadczących na rzecz sensowności przeprowadzania analizy składowych głównych.
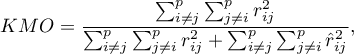
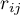 – współczynnik korelacji pomiędzy
– współczynnik korelacji pomiędzy  -tą a
-tą a  -tą zmienną,
-tą zmienną,
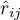 – współczynnik korelacji cząstkowej pomiędzy
– współczynnik korelacji cząstkowej pomiędzy  -tą a
-tą a  -tą zmienną.
-tą zmienną.
Wartość współczynnika Kaisera należy do przedziału 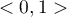 , gdzie wartości niskie świadczą o braku podstaw do przeprowadzania analizy składowych głównych, a wartości wysokie są przesłanką do przeprowadzania tej analizy.
, gdzie wartości niskie świadczą o braku podstaw do przeprowadzania analizy składowych głównych, a wartości wysokie są przesłanką do przeprowadzania tej analizy.
Ten klasyczny zestaw danych pierwotnie ukazał się w pracy R.A. Fishera 19361), gdzie przedstawiona została analiza dyskryminacyjna. Plik zawiera pomiary (w centymetrach) długości i szerokości płatków i działek kielicha dla 3 odmian kwiatu irysa. Poddane badaniu gatunki to setosa, versicolor i virginica. Interesujące jest określenie sposobu rozróżniania tych gatunków na bazie uzyskanych pomiarów.

Rycina pochodzi z pracy Lee i innych (2006r): „Application of a noisy data classification technique to determine the occurrence of flashover in compartment fires”
Analiza składowych głównych pozwoli na wskazanie tych pomiarów (długości i szerokości płatków i działek kielicha), które dają badaczowi najwięcej informacji o obserwowanych kwiatach.
Pierwszym etapem wykonywanym jeszcze przed przystąpieniem do wyznaczania i analizowania składowych, jest sprawdzenie celowości przeprowadzenia tej analizy. Zaczynamy więc od wyznaczenia macierzy korelacji zmiennych oraz przeanalizowania uzyskanych korelacji przy wykorzystaniu testu Bartletta i współczynnika KMO.
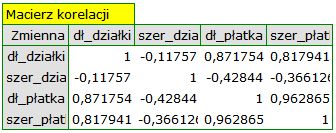
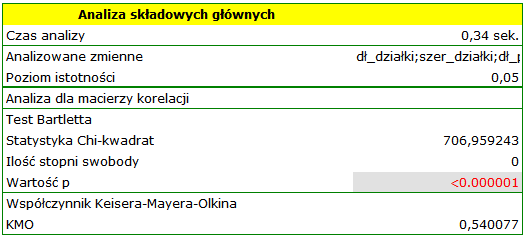
Wartość  statystyki Bartletta wskazuje na prawdziwość hipotezy mówiącej o istotnej różnicy pomiędzy uzyskaną macierzą korelacji a macierzą jednostkową, czyli znacznym skorelowaniu zmiennych. Uzyskany współczynnik KMO jest natomiast przeciętny i wynosi 0.54. Wskazania do przeprowadzenia analizy składowych głównych uznajemy za wystarczające.
statystyki Bartletta wskazuje na prawdziwość hipotezy mówiącej o istotnej różnicy pomiędzy uzyskaną macierzą korelacji a macierzą jednostkową, czyli znacznym skorelowaniu zmiennych. Uzyskany współczynnik KMO jest natomiast przeciętny i wynosi 0.54. Wskazania do przeprowadzenia analizy składowych głównych uznajemy za wystarczające.
Pierwszym wynikiem tej analizy, na który należy zwrócić szczególną uwagę są wartości własne:
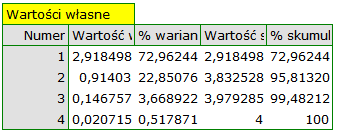
Uzyskane wartości własne wskazują, że dwie lub nawet jedna składowa główna w dobry sposób opiszą nasze dane. Wartość własna dla pierwszej składowej wynosi 2.92 a procent wyjaśnionej przez nią wariancji to 72.96. Druga składowa wyjaśnia już znacznie mniej wariancji, bo 22.85% a jej wartość własna to 0.91. Według kryterium Kaisera wystarczająca w interpretacji jest tylko jedna składowa główna, gdyż tylko dla pierwszej składowej wartość własna jest większa niż 1. Patrząc jednak na wykres osypiska można wysnuć wniosek, że linia spadkowa przechodzi w poziomą dopiero od 3 składowej głównej.
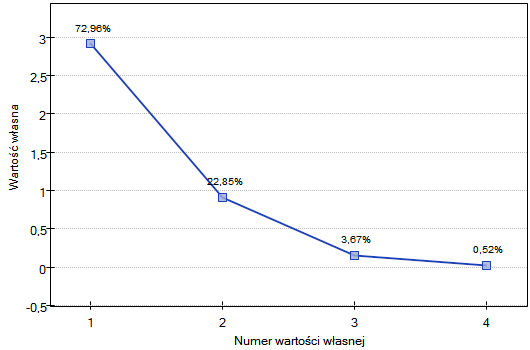
Zgodnie z tym wskazaniem dwie pierwsze składowe wnoszą istotną informację. Łącznie dwie pierwsze składowe wyjaśniają sporo bo aż 95.81% wariancji (patrz kolumna % skumulowany).
Zasoby zmienności wspólnej dla pierwszej składowej są wysokie dla wszystkich zmiennych pierwotnych za wyjątkiem zmiennej szerokość działki, dla której wynoszą 21,17%. Oznacza to, że gdybyśmy pozostali przy interpretacji tylko pierwszej składowej, to zmienna szerokość działki zostałaby odzwierciedlona w niewielkiej części.
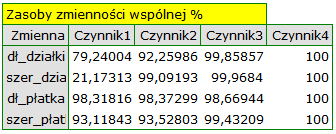
Dla dwóch pierwszych składowych zasoby zmienności wspólnej są już na podobnym, bardzo wysokim poziomie i dla każdej z analizowanych zmiennych przekraczają 90%, czyli wariancja każdej zmiennej jest reprezentowana przy użyciu tych składowych w ponad 90%.
Zebrawszy całą tą wiedzę zdecydowano się na wyodrębnienie i interpretację 2 składowych.
By przyjrzeć się dokładniej powiązaniu składowych głównych i zmiennych pierwotnych czyli długości i szerokości płatków i działek kielicha interpretujemy: wektory własne, ładunki czynnikowe oraz wkłady zmiennych.
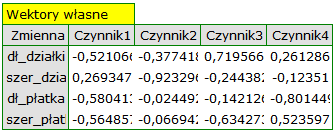
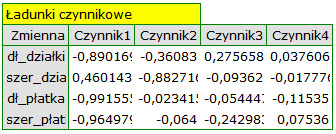
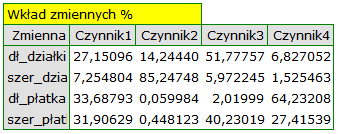
Poszczególne zmienne pierwotne w różny sposób oddziałują na pierwszą składową główną. Ułóżmy je kolejno według wielkości tego wpływu:
- Długość płatka jest ujemnie skorelowana z pierwszą składową, a zatem czym dłuższy płatek, tym niższe wartości tej składowej. Wektor własny dla długości płatka jest największy w tej składowej i wynosi -0.58. Jego ładunek czynnikowy informuje, że korelacja pomiędzy pierwszą składową główną a długością płatka jest bardzo wysoka i wynosi -0.99 co daje 33.69\% wkładu w pierwszą składową;
- Szerokość płatka ma nieco tylko mniejszy wpływ na pierwszą składową i jest z nią również ujemnie skorelowana;
- Długość działki interpretujemy podobnie jak poprzednie dwie zmienne ale jej wpływ na pierwszą składową jest mniejszy;
- Szerokość działki jest najsłabiej skorelowana z pierwszą składową i znak tej korelacji jest dodatni.
Druga składowa reprezentuje głównie zmienną pierwotną: szerokość działki; pozostałe zmienne pierwotne są w niej odzwierciedlone w niewielkim stopniu. Wektor własny, ładunek czynnikowy oraz wkład zmiennej szerokość działki jest w składowej drugiej najwyższy.
Każda składowa główna wyznacza homogeniczną grupę zmiennych pierwotnych. Pierwszą składową nazwiemy „rozmiar płatka”, gdyż najbardziej znaczącymi dla niej zmiennymi są te zmienne, które niosą informacje o płatku, choć trzeba zaznaczyć, że długość działki również wpływa znacznie na wartość tej składowej. W interpretacji pamiętamy, że czym większe są wartości tej składowej , tym mniejsze są płatki.
Drugą składową nazwiemy natomiast „szerokość działki” gdyż tylko szerokość działki w większym stopniu odzwierciedlona jest w drugiej składowej. Przy czym, im większe są wartości tej składowej, tym węższa jest działka.
Ostatecznie składowe wygenerujemy wybierając w oknie analizy opcję: Dołącz składowe główne. Fragment uzyskanego wyniku przedstawiamy poniżej:
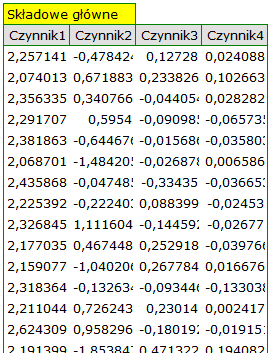
Aby dwie pierwsze składowe można było wykorzystać zamiast wcześniejszych czerech zmiennych pierwotnych, ostatecznie przeklejamy je do arkusza danych. Dalsze planowane przez siebie statystyki badacz może teraz przeprowadzić na dwóch nowych, nieskorelowanych zmiennych.
- [Analiza wykresów dwóch pierwszych składowych]
Analiza wykresów nie dość, że doprowadzi badacza do tych samych wniosków, co analiza tabel, to da możliwość wnikliwszej oceny uzyskanych wyników. - [Wykres ładunków czynnikowych]
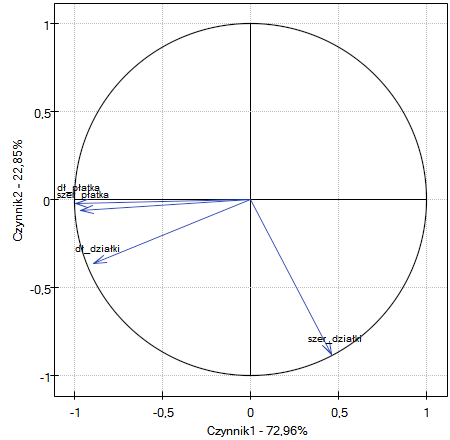
Wykres przedstawia dwie pierwsze składowe główne, które reprezentują 72.96% wariancji i 22.85% wariancji co daje łącznie 95.81% wariancji zmiennych pierwotnych
Wektory reprezentujące zmienne pierwotne nieomalże sięgają brzegów koła jednostkowego (koła o promieniu 1), a zatem wszystkie one są bardzo dobrze reprezentowane przez dwie pierwsze składowe główne tworzące układ współrzędnych.
Kąt pomiędzy wektorami obrazującymi długość płatka, szerokość płatka i długość działki jest niewielki, co oznacza duże skorelowanie tych zmiennych. Skorelowanie zaś tych zmiennych ze składowymi tworzącymi układ jest negatywne - wektory znajdują się w III ćwiartce układu. Przy czym wyższe wartości współrzędnych końca wektora obserwowane są dla składowej pierwszej niż drugiej. Takie ułożenie wektorów świadczy o tym, że tworzą one grupę jednorodną, która jest reprezentowana głównie przez składową pierwszą.
Zupełnie inny kierunek wskazuje wektor dotyczący szerokości działki, który jest w niewielkim stopniu skorelowany z pozostałymi zmiennymi pierwotnymi o czym świadczy kąt nachylenia do pozostałych zmiennych pierwotnych, który jest bliski kątowi prostemu. Skorelowanie tego wektora z pierwszą składową jest pozytywne i niezbyt wysokie (niska wartość pierwszej współrzędnej końca wektora) a z drugą składową negatywne i wysokie (wysoka wartość drugiej współrzędnej końca wektora). Wnioskujemy z tego, że szerokość działki jako jedyna zmienna pierwotna reprezentowana jest dobrze przez drugą składową.
- [Biplot]
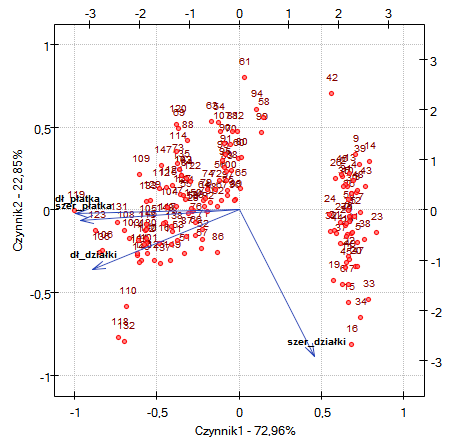
Biplot przedstawia dwie serie danych rozpięte na dwóch pierwszych składowych. Jedną serią są wektory zmiennych pierwotnych, które przedstawione były na poprzednim wykresie, a drugą serią są punkty niosące informacje o poszczególnych kwiatach. Przy czym wartości drugiej serii odczytujemy na górnej osi  i prawej osi
i prawej osi  . Sposób interpretacji wektorów, czyli pierwszej serii omówiliśmy przy poprzednim wykresie. By zrozumieć interpretację punktów skupimy się na kwiatach o numerze 33 i 34 oraz o numerze 109.
. Sposób interpretacji wektorów, czyli pierwszej serii omówiliśmy przy poprzednim wykresie. By zrozumieć interpretację punktów skupimy się na kwiatach o numerze 33 i 34 oraz o numerze 109.
Kwiaty o numerze 33 i 34 są do siebie podobne - odległość punktu 33 i 34 jest niewieka. Oba punkty mają sporo większą niż przeciętna wartość pierwszej i sporo mniejszą niż przeciętna wartość drugiej składowej. Wartość przeciętna, a zatem średnia arytmetyczna obu składowych wynosi 0, więc jest to środek układu współrzędnych. Pamiętając, że pierwsza składowa to głównie rozmiar płatków a druga to szerokość działki możemy powiedzieć, że kwiaty 33 i 34 mają niewielkie płatki i dużą szerokość działki. Natomiast kwiat 109 reprezentuje punkt znacznie oddalony od pozostałych dwóch punktów. Jest to kwiat o ujemnej pierwszej składowej i dodatniej lecz nie wysokiej drugiej składowej. Zatem jest to kwiat o stosunkowo dużych płatkach i szerokości działki nieco tylko mniejszej niż przeciętna.
Podobne informacje uzyskamy rzutując punkty na linie przedłużające wektory zmiennych pierwotnych. Przykładowo kwiat 33 wykazuje się dużą szerokością działki (wysokie i dodatnie wartości rzutowania na zmienną pierwotną szerokość działki) ale niskimi wartościami pozostałych zmiennych pierwotnych (ujemne wartości rzutowania na przedłużenie wektorów obrazujących pozostałe zmienne pierwotne).
2014/08/22 20:00
2014/08/22 20:00
Analiza skupień
Analiza skupień to szereg metod dzielenia obiektów, bądź cech (zmiennych) na podobne grupy. Zasadniczo metody te dzieli się na dwie klasy: metody hierarchiczne i niehierarchiczne jak metoda k-średnich. W swoich algorytmach obie metody wykorzystują macierz podobieństwa, by na jego podstawie tworzyć skupienia.
Grupowanie obiektów i grupowanie zmiennych odbywa się w analizie skupień dokładnie w ten sam sposób. W rozdziale tym metody grupowania opisane zostaną na przykładzie grupowania obiektów.
Uwaga! Chcąc zapewnić zrównoważony wpływ wszystkich zmiennych na elementy macierzy podobieństwa, dane należy poddać standaryzacji wybierając odpowiednią opcję w oknie analizy. Brak standaryzacji daje większy wpływ na uzyskany wynik zmiennym wyrażonym większymi liczbami.
Metody hierarchiczne
Metody hierarchicznej analizy skupień polegają na budowaniu hierarchii skupień poczynając od tych najmniejszych (złożonych z pojedynczych obiektów), a kończąc na tych największych (złożonych z maksymalnej liczby obiektów). Skupienia tworzone są na bazie macierzy podobieństwa obiektów.
PROCEDURA AGLOMERACYJNA
- Postępując zgodnie z wskazaną metodą wiązania, algorytm znajduje w macierzy podobieństwa parę podobnych obiektów i łączy je w skupienie;
- Wymiar macierzy podobieństwa zostaje zredukowany o jeden (dwa obiekty zastąpiono jednym) a odległości znajdujące się w macierzy wyliczone są ponownie;
- Kroki 2-3 są powtarzane aż do uzyskania jednego skupienia zawierającego wszystkie obiekty.
Podobieństwo obiektów
W toku prac związanych z analizą skupień zasadniczą rolę odgrywają miary podobieństwa lub odległości. Wzajemne podobieństwo obiektów umieszczane jest w macierzy podobieństwa. Duża różnorodność metod wyznaczania odległości/niepodobieństwa między obiektami pozwala na wybór takich miar, które najlepiej odzwierciedlają rzeczywiste relacje. Szerzej miary odległości i podobieństwa opisane są w dziale Macierz podobieństwa.
Analiza skupień opiera swoje działania na wyszukiwaniu skupień wewnątrz macierzy podobieństwa. Macierz taka jest budowana w trakcie wykonywania analizy skupień. By analiza skupień przyniosła pożądane skutki, przy wyborze sposobu wyliczania odległości należy pamiętać, że większe wartości liczbowe w macierzy podobieństwa mają wskazywać na większe zróżnicowanie obiektów, a wartości mniejsze na ich podobieństwo.
Uwaga! By zwiększyć wpływ wybranych zmiennych na elementy macierzy podobieństwa, należy wskazać odpowiednie wagi przy ustawianiu sposobu definiowania odległości pamiętając jednocześnie o wystandaryzowaniu danych. Np. Dla osób chcących zaopiekować się psem pogrupowanie psów zgodnie z wielkością, umaszczeniem, długością ogona, charakterem, rasą itp. ułatwi dokonanie wyboru. Jednak, identyczne traktowanie wszystkich cech może spowodować umieszczenie zupełnie niepodobnych psów w jednej grupie. Natomiast dla większości z nas ważniejsza jest wielkość psa i jego charakter niż długość jego ogona, dlatego w grupowaniu należałoby ustawić miary podobieństwa tak, by to właśnie wielkość i charakter miały największe znaczenie w budowaniu skupień.
Metody wiązania obiektów i skupień
- Metoda pojedynczego wiązania (najbliższe sąsiedztwo) - odległość pomiędzy skupieniami określona jest poprzez odległość tych obiektów każdego skupienia, które znajdują się najbliżej siebie.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(1.7,0.1)(5.1,-0.4)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imge1a5de3e36c331f92bb1ddd197ffcc63.png)
- Metoda pełnego wiązania (najdalsze sąsiedztwo) - odległość pomiędzy skupieniami określona jest poprzez odległość tych obiektów każdego skupienia, które znajdują się najdalej siebie.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(-.8,1)(7.2,1.2)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgd86738754d560f3b0b517c3b97807da1.png)
- Metoda średnich połączeń - odległość pomiędzy skupieniami określona jest poprzez średnią odległość pomiędzy wszystkimi parami obiektów zlokalizowanych w obrębie dwóch różnych skupień.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(-.8,1)(7.2,1.2)
\psline{-}(-.8,1)(5.1,-0.4)
\psline{-}(-.8,1)(5.6,1.3)
\psline{-}(1.7,0.1)(7.2,1.2)
\psline{-}(1.7,0.1)(5.1,-0.4)
\psline{-}(1.7,0.1)(5.6,1.3)
\psline{-}(0.6,1.2)(7.2,1.2)
\psline{-}(0.6,1.2)(5.1,-0.4)
\psline{-}(1.7,0.1)(5.6,1.3)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img74722956ba453f9c18004ab4885a71f4.png)
- Metoda średnich połączeń ważonych - analogicznie do metody średnich połączeń polega na wyliczeniu średniej odległości, ale średnia ta ważona jest poprzez liczbę elementów każdego skupienia. W rezultacie powinniśmy wybierać tę metodę, gdy oczekujemy uzyskać skupienia o podobnych licznościach.
- Metoda Warda - opiera się na zasadzie analizy wariancji - wylicza różnicę między sumami kwadratów odchyleń odległości poszczególnych obiektów od środka ciężkości skupienia, do których te obiekty należą. Metoda ta wybierana jest najczęściej ze względu na jej dość uniwersalny charakter.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\psline[linestyle=dashed]{-}(-.8,1)(0.52,0.8)
\psline[linestyle=dashed]{-}(1.7,0.1)(0.52,0.8)
\psline[linestyle=dashed]{-}(0.6,1.2)(0.52,0.8)
\psdot[dotstyle=pentagon*,linecolor=red](0.52,0.8)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psdot[dotstyle=pentagon*,linecolor=red](5.85,0.8)
\psline[linestyle=dashed]{-}(7.2,1.2)(5.85,0.8)
\psline[linestyle=dashed]{-}(5.1,-0.4)(5.85,0.8)
\psline[linestyle=dashed]{-}(5.6,1.3)(5.85,0.8)
\psline[linestyle=dotted]{-}(0.52,0.8)(5.85,0.8)
\psline[linestyle=dotted]{-}(-.8,1)(7.2,1.2)
\psline[linestyle=dotted]{-}(-.8,1)(5.1,-0.4)
\psline[linestyle=dotted]{-}(-.8,1)(5.6,1.3)
\psline[linestyle=dotted]{-}(1.7,0.1)(7.2,1.2)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.1,-0.4)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.6,1.3)
\psline[linestyle=dotted]{-}(0.6,1.2)(7.2,1.2)
\psline[linestyle=dotted]{-}(0.6,1.2)(5.1,-0.4)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.6,1.3)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img169789b519f1a291561b77a1301c7fc1.png)
Wynik analizy skupień prowadzonej metodą hierarchiczną przedstawia się przy pomocy dendogramu. Dendogram jest formą drzewa wskazującego związki pomiędzy poszczególnymi obiektami uzyskane z analizy macierzy podobieństwa. Poziom odcięcia dendogramu decyduje o liczbie skupień, na które chcemy dzielić zgromadzone obiekty. Wybór sposobu odcięcia określamy podając w procentach długość wiązania, przy którym nastąpi cięcie, gdzie 100% stanowi długość ostatniego i jednocześnie najdłuższego wiązania w dendogramie.
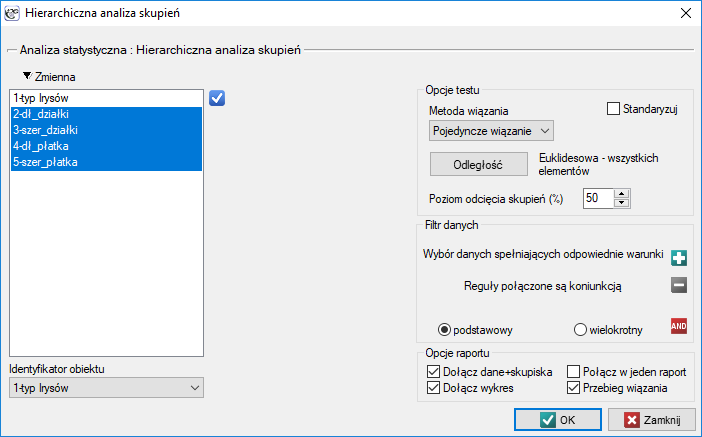
Okno z ustawieniami opcji hierarchicznej analizy skupień wywołujemy poprzez menu Statystyki zaawansowane→Grupowanie i Redukcja→Hierarchiczna analiza skupień.
Przykład c.d. (plik iris.pqs)
Analiza przeprowadzona zostanie na klasycznym zestawie danych, dotyczącym podziału kwiatów irysa na 3 odmiany na podstawie szerokości oraz długości płatków i działek kielicha (R.A. Fishera 19362)). Ponieważ w tym zestawie danych znajduje się informacja o rzeczywistej odmianie każdego kwiatu, po przeprowadzonej analizie skupień istnieje możliwość określenia dokładności dokonanego podziału.
Przydziału kwiatów do poszczególnych grup dokonujemy na podstawie kolumn od 2 do 5. Wybieramy sposób wyliczania odległości np. odległość Euklidesową i metodę wiązania np. średnią. Podanie poziomu odcięcia skupień pozwoli na takie odcięcie dendogramu by powstały skupienia - w przypadku tej analizy chcemy uzyskać 3 skupienia i by to osiągnąć zmieniamy poziom odcięcia na 45%. Do raportu dołączamy również dane+skupienia.

Na wykresie typu dendogram, przedstawiono kolejność wiązań i ich długość.
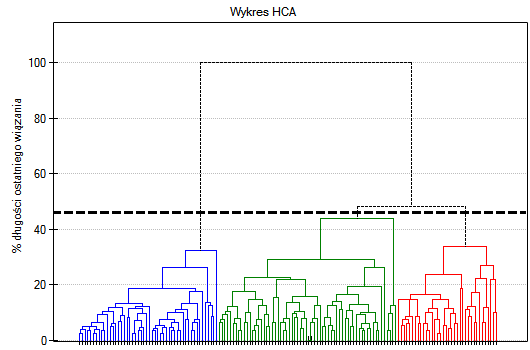
By zbadać czy wyodrębnione skupienia stanowią 3 rzeczywiste odmiany kwiatów irysa, możemy skopiować kolumnę zawierającą informację o przynależności do skupienia z raportu i wkleić do arkusza danych. Podobnie jak skupienia, odmiany opisane są również liczbowo poprzez Kody/Etykiety/Format, dlatego z łatwością można przeprowadzić analizę zgodności. Zgodność naszych wyników z rzeczywistą przynależnością danego kwiatu do odpowiedniego gatunku sprawdzimy metodą Kappa Cohena.
Dla przedstawionego przykładu obserwowaną zgodność przedstawia tabela:
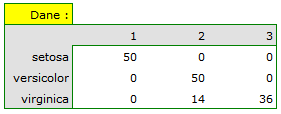
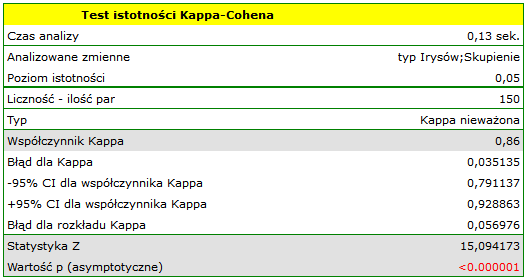
Wnioskujemy z niej, że odmiana virginica może być mylona z versicolor, dlatego obserwujemy tu 14 błędnych zaklasyfikowań. Natomiast współczynnik zgodności Kappa jest istotny statystycznie i wynosi 0.86, co świadczy o dużej zgodności uzyskanych skupień z rzeczywistą odmianą kwiatów.
2015/12/28 12:15
· admin
Metoda k-średnich
Metoda k-średnich (ang. k-means) wzoruje swoje działanie na algorytmie zaproponowanym początkowo przez Stuarta Lloyda i opublikowana w roku 1982 3). W metodzie tej obiekty dzieli się na z góry założoną liczbę  skupień. Początkowe skupienia poprawia się w toku wykonywania procedury aglomeracji, przenosząc pomiędzy nimi obiekty tak by zróżnicowanie obiektów wewnątrz skupienia było jak najmniejsze a odległości skupień jak największe. Algorytm działa w oparciu o macierz odległości euklidesowych pomiędzy obiektami, a parametrami niezbędnymi w procedurze aglomeracji metody k-średnich są: centra startowe i kryterium stopu. Centra startowe są to obiekty od których algorytm rozpocznie budowę skupień, a kryterium stopu to określenie sposobu zatrzymania algorytmu.
skupień. Początkowe skupienia poprawia się w toku wykonywania procedury aglomeracji, przenosząc pomiędzy nimi obiekty tak by zróżnicowanie obiektów wewnątrz skupienia było jak najmniejsze a odległości skupień jak największe. Algorytm działa w oparciu o macierz odległości euklidesowych pomiędzy obiektami, a parametrami niezbędnymi w procedurze aglomeracji metody k-średnich są: centra startowe i kryterium stopu. Centra startowe są to obiekty od których algorytm rozpocznie budowę skupień, a kryterium stopu to określenie sposobu zatrzymania algorytmu.
PROCEDURA AGLOMERACYJNA
- Wybór centów startowych
- Bazując na macierzy podobieństwa algorytm przypisuje każdy obiekt do najbliższego centrum
- Dla uzyskanych skupień wyznacza się poprawione centra.
- Kroki 2-3 są powtarzane aż do momentu spełnienia kryterium stopu.
Centra startowe
Wybór centrów startowych ma zasadniczy wpływ na zbieżność algorytmu k-średnich dla uzyskania odpowiednich skupień. Centra startowe mogą być wybrane na dwa sposoby:
- k-means++ - to optymalny dobór punktów startowych poprzez wykorzystanie algorytmu k-means++ zaproponowanego w 2007 roku przez David Arthur and Sergei Vassilvitskii 4). Gwarantuje on uzyskanie optymalnego rozwiązania algorytmu k-średnich przy możliwie niewielu iteracjach. Algorytm wykorzystuje w swoim działaniu element losowości, dlatego uzyskiwane wyniki mogą się nieco różnić przy kolejnych uruchomieniach analizy. Jeśli dane nie formułują się w naturalne klastery, lub jeśli nie można skutecznie podzielić danych na rozłączne skupiska, użycie k-means++ spowoduje uzyskanie zupełnie innych wyników w kolejnych uruchomieniach analizy k-średnich. Duża powtarzalność wyników świadczy natomiast o możliwości dokonania dobrego podziału na oddzielne skupienia.
- n pierwszych - pozwala by użytkownik wskazał punkty będące centrami startowymi poprzez ustawienie tych obiektów na pierwszych miejscach w tabeli danych.
Kryterium stopu jest to moment, w którym nie zmienia się przynależność punktów do klas lub liczba powtórzeń kroku 2 i 3 algorytmu osiągnie zadaną przez użytkownika liczbę iteracji.
Ze względu na sposób działania algorytmu analizy skupień k-średnich, naturalną jej konsekwencją jest porównanie powstałych skupień przy pomocy jednoczynnikowej analizy wariancji (ANOVA) dla grup niezależnych.
Okno z ustawieniami opcji analizy skupień k-średnich wywołujemy poprzez menu Statystyki zaawansowane→Grupowanie i Redukcja→Analiza skupień k-średnich.
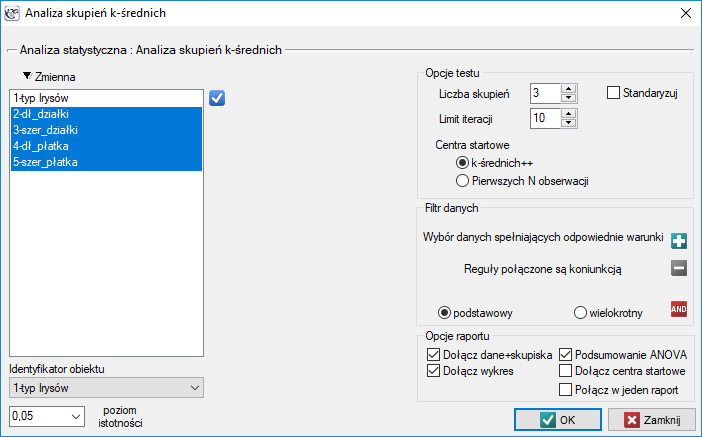
Przykład c.d. (plik iris.pqs)
Analiza przeprowadzona zostanie na klasycznym zestawie danych, dotyczącym podziału kwiatów irysa na 3 odmiany na podstawie szerokości oraz długości płatków i działek kielicha (R.A. Fishera 19365)).
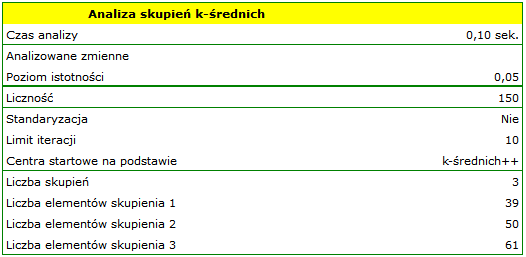
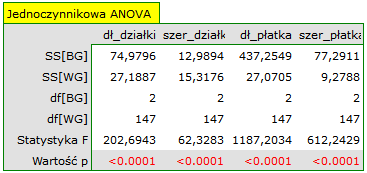
Przydziału kwiatów do poszczególnych grup dokonujemy na podstawie kolumn od 2 do 5. Wskazujemy również, że badane kwiaty chcemy podzielić na 3 grupy. W rezultacie przeprowadzonej analizy utworzono 3 skupienia, które różnią się istotnie statystycznie w każdym badanym wymiarze (wyniki ANOVA), czyli dla szerokości płatka, długości płatka, szerokości kielicha jaki i długości kielicha.
Różnicę można zaobserwować na wykresach, gdzie przedstawiamy w wybranych dwóch wymiarach przynależność poszczególnych punktów do skupień:
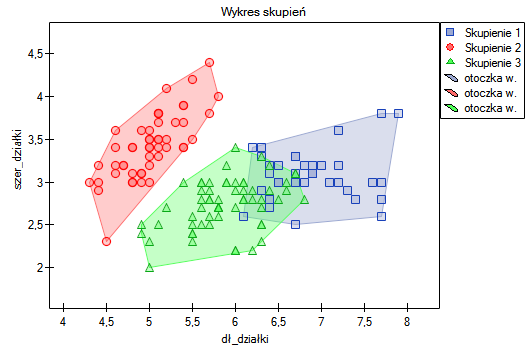
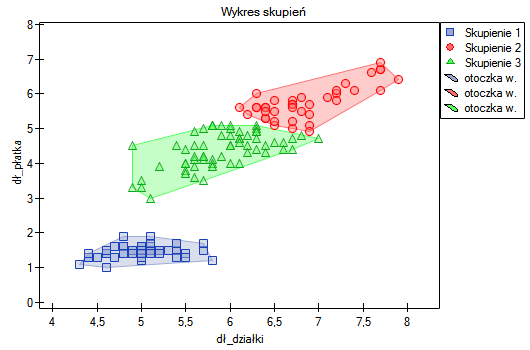
Powtarzając analizę możemy uzyskać nieco inne wyniki, ale uzyskana zmienność nie będzie duża. Świadczy to o tym, że dane poddane analizie formułują się w naturalne skupiska i przeprowadzanie analizy skupień jest w tym przypadku uzasadnione.
Uwaga 1!
Po kilkukrotnym przeprowadzeniu analizy możemy wybrać najbardziej interesujący nas wynik, a następnie ustawić te dane, które stanowią centra startowe na początku arkusza - wówczas analiza przeprowadzona w oparciu o centra startowe wybierane jako N pierwszych obserwacji będzie dawała stale ten wybrany przez nas efekt.
Uwaga 2! By dowiedzieć się czy skupienia stanowią 3 rzeczywiste odmiany kwiatów irysa, możemy skopiować informację o przynależności do skupień z raportu i wkleić do arkusza danych. Zgodność naszych wyników z rzeczywistą przynależnością danego kwiatu do odpowiedniego gatunku możemy sprawdzić analogicznie jak dla hierarchicznej analizy skupień.
2015/12/28 12:25
· admin
2015/12/28 12:14
· admin
1)
, 2)
, 5)
Fisher R.A. (1936), The use of multiple measurements in taxonomic problems. Annals of Eugenics 7 (2): 179–188
3)
Lloyd S. P. (1982), Least squares quantization in PCM. IEEE Transactions on Information Theory 28 (2): 129–137
4)
Arthur D., Vassilvitskii S. (2007), k-means++: the advantages of careful seeding. Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics Philadelphia, PA, USA. 1027–1035
statpqpl/redpl.txt · ostatnio zmienione: 2019/12/17 17:30 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

