Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:zgodnpl:nparpl:kappalpl
Współczynnik Kappa Cohena i test badający jego istotność
Współczynnik Kappa Cohena (ang. Cohen's Kappa), Cohen J. (1960)1), określa stopień zgodności dwukrotnych pomiarów tej samej zmiennej w różnych warunkach. Pomiaru tej samej zmiennej może dokonać dwóch różnych sędziów (odtwarzalność) lub jeden sędzia może dokonać pomiaru dwukrotnie (powtarzalność). Współczynnik  wyznacza się dla zależnych zmiennych kategorialnych, a jego wartość zawiera się w przedziale od -1 do 1. Wartość 1 oznacza pełną zgodność, wartość 0 oznacza zgodność na poziomie takim samym jaki powstałby dla losowego rozłożenia danych w tabeli kontyngencji. Poziom pomiędzy 0 a -1 jest w praktyce niewykorzystywany. Ujemna wartość
wyznacza się dla zależnych zmiennych kategorialnych, a jego wartość zawiera się w przedziale od -1 do 1. Wartość 1 oznacza pełną zgodność, wartość 0 oznacza zgodność na poziomie takim samym jaki powstałby dla losowego rozłożenia danych w tabeli kontyngencji. Poziom pomiędzy 0 a -1 jest w praktyce niewykorzystywany. Ujemna wartość  oznacza zgodność na poziomie mniejszym niż powstała dla losowego rozłożenia danych w tabeli kontyngencji. Współczynnik
oznacza zgodność na poziomie mniejszym niż powstała dla losowego rozłożenia danych w tabeli kontyngencji. Współczynnik  można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach
można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach 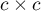 .
.
W zależności od potrzeb można wyznaczać Kappę nieważoną (czyli Kappę Cohena) lub Kappę ważoną. Przydzielane wagi (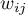 ) odnoszą się do poszczególnych komórek tabeli kontyngencji, na przekątnej wynoszą 1 a poza przekątną należą do przedziału
) odnoszą się do poszczególnych komórek tabeli kontyngencji, na przekątnej wynoszą 1 a poza przekątną należą do przedziału 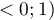 .
.
Kappa nieważona
Wyliczana jest dla danych, których kategorii nie da się uporządkować np. dane pochodzą od pacjentów, których dzielimy ze względu na rodzaj choroby jaka została zdiagnozowana, a chorób tych nie można uporządkować np. zapalenie płuc 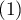 , zapalenie oskrzeli
, zapalenie oskrzeli 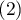 i inne
i inne 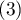 . W takiej sytuacji można sprawdzać zgodność diagnoz wystawionych przez dwóch lekarzy stosując nieważoną Kappę, czyli Kappę Cohena. Niezgodność par
. W takiej sytuacji można sprawdzać zgodność diagnoz wystawionych przez dwóch lekarzy stosując nieważoną Kappę, czyli Kappę Cohena. Niezgodność par 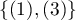 oraz
oraz 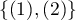 traktowana będzie równoważnie, a więc wagi poza przekątną macierzy wag będą zerowane.
traktowana będzie równoważnie, a więc wagi poza przekątną macierzy wag będą zerowane.
Kappa ważona
W sytuacji kiedy kategorie danych mogą być posortowane np. dane pochodzą od pacjentów, których dzielimy ze względu na stopień zmian chorobowych na: brak zmian 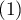 , zmiany łagodne
, zmiany łagodne 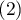 , podejrzenie raka
, podejrzenie raka 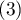 , rak
, rak 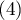 , budować można zgodność wystawionych ocen przez dwóch radiologów uwzględniając możliwość sortowania. Za bardziej niezgodne pary ocen mogą być wówczas uznane oceny
, budować można zgodność wystawionych ocen przez dwóch radiologów uwzględniając możliwość sortowania. Za bardziej niezgodne pary ocen mogą być wówczas uznane oceny 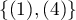 niż
niż 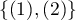 . By tak było, by kolejność kategorii wpływała na wynik zgodności, wyznaczać należy ważoną Kappę.
. By tak było, by kolejność kategorii wpływała na wynik zgodności, wyznaczać należy ważoną Kappę.
Przydzielane wagi mogą mieć postać liniową lub kwadratową.
- Wagi liniowe (Cicchetti, 19712)) - wyliczane według wzoru:
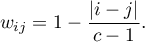
Czym większe oddalenie od przekątnej macierzy tym mniejsza waga, przy czym wagi maleją proporcjonalnie. Przykładowe wagi dla macierzy wielkości 5×5 przedstawia tabela:
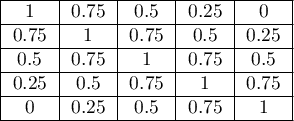
- Wagi kwadratowe (Cohen, 19683)) - wyliczane według wzoru:
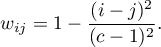
Czym większe oddalenie od przekątnej macierzy tym mniejsza waga, przy czym wagi maleją wolniej w bliższej odległości od przekątnej i szybciej w odległości dalszej. Przykładowe wagi dla macierzy wielkości 5×5 przedstawia tabela:
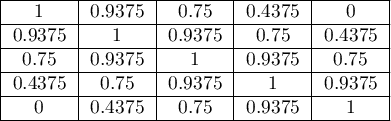
Wagi kwadratowe cieszą się większym zainteresowaniem ze względu na praktyczną interpretację współczynnika Kappa, który w tym przypadku tożsamy jest ze współczynnikiem korelacji wewnątrzklasowej 4).
By wyznaczyć zgodność współczynnikiem Kappa dane przedstawia się w postaci tabeli liczności obserwowanych 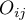 , dalej tą tabelę przekształca się w tabelę kontyngencji prawdopodobieństw
, dalej tą tabelę przekształca się w tabelę kontyngencji prawdopodobieństw 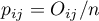 .
.
Współczynnik Kappa ( ) wyraża się wtedy wzorem:
) wyraża się wtedy wzorem:
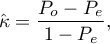
gdzie:
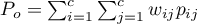 ,
,
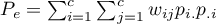 ,
,
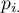 ,
, 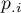 - sumy końcowe kolumn i wierszy tabeli kontyngencji prawdopodobieństw.
- sumy końcowe kolumn i wierszy tabeli kontyngencji prawdopodobieństw.
Uwaga!
 oznacza współczynnik zgodności w próbie, natomiast
oznacza współczynnik zgodności w próbie, natomiast 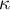 w populacji.
w populacji.
Błąd standardowy dla Kappa wyraża się wzorem:
![LaTeX \begin{displaymath}
SE_{\hat \kappa}=\frac{1}{(1-P_e)\sqrt{n}}\sqrt{\sum_{i=1}^{c}\sum_{j=1}^{c}p_{i.}p_{.j}[w_{ij}-(\overline{w}_{i.}+(\overline{w}_{.j})]^2-P_e^2}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img059555813b7a0927359f9000c829f6fe.png) gdzie:
gdzie:
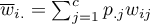 ,
,
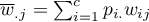 .
.
Test Z do sprawdzania istotności współczynnika Kappa Cohena ( ) (ang. The Z test of significance for the Cohen's Kappa) Fleiss (20035)) służy do weryfikacji hipotezy o zgodności wyników dwukrotnych pomiarów
) (ang. The Z test of significance for the Cohen's Kappa) Fleiss (20035)) służy do weryfikacji hipotezy o zgodności wyników dwukrotnych pomiarów 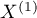 i
i 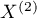 cechy
cechy  i opiera się na współczynniku
i opiera się na współczynniku  wyliczonym dla próby.
wyliczonym dla próby.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej (Kappa Cohena - nieważona) i skali porządkowej (Kappa ważona).
Hipotezy:
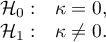
Statystyka testowa ma postać:
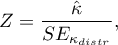
gdzie:
![LaTeX $\displaystyle{SE_{\kappa_{distr}}=\frac{1}{(1-P_e)\sqrt{n}}\sqrt{\sum_{i=1}^c\sum_{j=1}^c p_{ij}[w_{ij}-(\overline{w}_{i.}+\overline{w}_{.j})(1-\hat \kappa)]^2-[\hat \kappa-P_e(1-\hat \kappa)]^2}}$](/lib/exe/fetch.php?media=wiki:latex:/imgc30723ad5a68d25b44687da3bff2c069.png) .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji testu istotności Kappa-Cohena wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Kappa-Cohena lub poprzez Kreator.
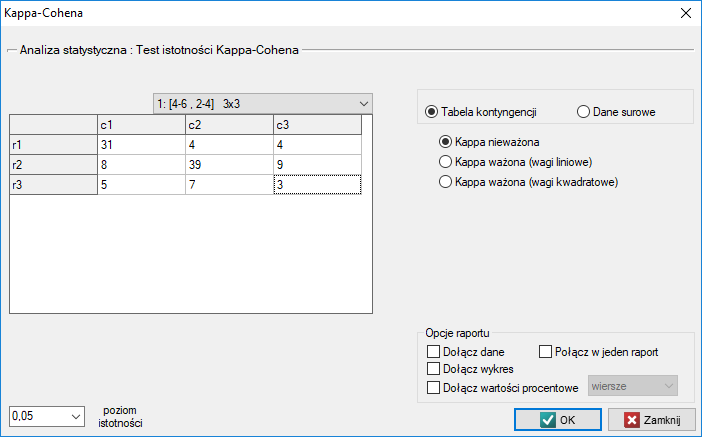
Badamy zgodność diagnozy postawionej przez 2 lekarzy. W tym celu pobieramy próbę 110 pacjentów szpitala dziecięcego. Lekarze przyjmują pacjentów w sąsiednich gabinetach. Każdy z pacjentów jest najpierw badany przez lekarza A a następnie przez lekarza B. Diagnozy postawione przez lekarzy przedstawia poniższa tabela.

Hipotezy:
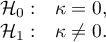
Moglibyśmy badać zgodność diagnozy poprzez zwykły procent wartości zgodnych. W naszym przykładzie zgodną diagnozę lekarze postawili dla 73 pacjentów (31+39+3=73) co stanowi 66.36% badanej grupy. Współczynnik Kappa wprowadza korekcję tej wartości o szanse na zgodność (tzn. w korekcji o tę zgodność, która pojawia się dla przypadkowego rozłożenia danych w tabeli).
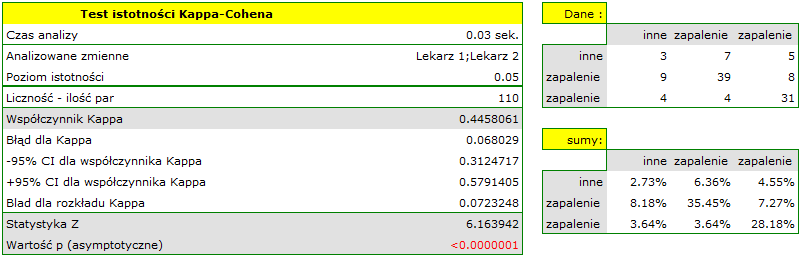
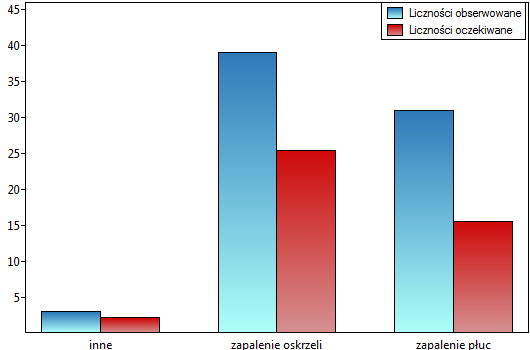
Zgodność wyrażona współczynnikiem 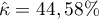 jest mniejsza niż ta nie skorygowana o szanse na zgodność.
jest mniejsza niż ta nie skorygowana o szanse na zgodność.
Wartość 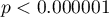 . Wynik taki, na poziomie istotności
. Wynik taki, na poziomie istotności  , świadczy o zgodności opinii tych 2 lekarzy.
, świadczy o zgodności opinii tych 2 lekarzy.
Przykład (plik radiologia.pqs)
W obrazie radiologicznym oceniano uszkodzenie wątroby w następujących kategoriach: brak zmian 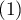 , zmiany łagodne
, zmiany łagodne 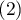 , podejrzenie raka
, podejrzenie raka 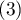 , rak
, rak 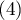 . Oceny dokonywało dwóch niezależnych radiologów bazując na grupie 70 pacjentów. Chcemy sprawdzić zgodność postawionej diagnozy.
. Oceny dokonywało dwóch niezależnych radiologów bazując na grupie 70 pacjentów. Chcemy sprawdzić zgodność postawionej diagnozy.
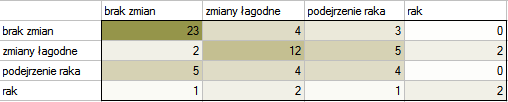
Hipotezy:
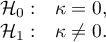
Ze względu na to, że diagnoza wystawiona jest na skali porządkowej, właściwą miarą zgodności byłby ważony współczynnik Kappa.

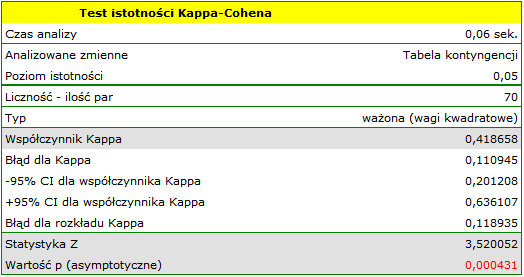
Ponieważ dane koncentrują się głównie na głównej przekątnej macierzy i w jej bliskim sąsiedztwie, współczynnik ważony wagami liniowymi jest niższy (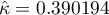 ) niż współczynnik wyznaczony dla wag kwadratowych (
) niż współczynnik wyznaczony dla wag kwadratowych (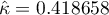 ). W obu sytuacjach jest to wynik istoty statystycznie (na poziomie istotności
). W obu sytuacjach jest to wynik istoty statystycznie (na poziomie istotności  ), wartość
), wartość  wynosi odpowiednio: 0.000007 i 0.000431.
wynosi odpowiednio: 0.000007 i 0.000431.
Gdyby w ocenach istniała duża niezgodność dotycząca dwóch skrajnych przypadków i para: (brak zmian i rak) znajdująca się w prawym górnym roku tabeli występowała zdecydowanie częściej, np. 15 razy, wówczas taki duży brak zgodności widoczny będzie bardziej, gdy wykorzystamy wagi kwadratowe (współczynnik Kappa drastycznie spadnie) niż przy wykorzystaniu wag liniowych.
1)
Cohen J. (1960), A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 10,3746
2)
Cicchetti D. and Allison T. (1971), A new procedure for assessing reliability of scoring eeg sleep recordings. American Journal EEG Technology, 11, 101-109
3)
Cohen J. (1968), Weighted kappa: nominal scale agreement with provision for scaled disagreement or partial credit. Psychological Bulletin, 70, 213-220
4)
Fleiss J.L., Cohen J. (1973), The equivalence of weighted kappa and the intraclass correlation coeffcient as measure of reliability. Educational and Psychological Measurement, 33, 613-619
5)
Fleiss J.L., Levin B., Paik M.C. (2003), Statistical methods for rates and proportions. 3rd ed. (New York: John Wiley) 598-626
statpqpl/zgodnpl/nparpl/kappalpl.txt · ostatnio zmienione: 2022/01/23 21:27 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


