Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:zgodnpl
Spis treści
Analiza zgodności
{\ovalnode{A}{\hyperlink{rozklad_normalny}{\begin{tabular}{c}Czy rozkład\\zmiennej jest\\rozkładem\\normalnym?\end{tabular}}}}
\rput[br](3.7,6.2){\rnode{B}{\psframebox{\hyperlink{ICC}{\begin{tabular}{c}test\\do sprawdzania\\istotności\\współczynnika\\zgodności\\wewnątrzklasowej $r_{ICC}$\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{B}
\rput(2.2,10.4){T}
\rput(4.3,12.5){N}
\rput(7.5,14){\hyperlink{porzadkowa}{Skala porządkowa}}
\rput[br](9.4,10.8){\rnode{C}{\psframebox{\hyperlink{Kendall_W}{\begin{tabular}{c}test\\do sprawdzania\\istotności\\współczynnika\\zgodności\\$\widetilde{W}$ Kendalla \end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{C}
\rput(12.5,14){\hyperlink{nominalna}{Skala nominalna}}
\rput[br](14.2,10.8){\rnode{D}{\psframebox{\hyperlink{wspolczynnik_Kappa}{\begin{tabular}{c}test\\do sprawdzania\\istotności\\współczynnika\\zgodności\\$\hat \kappa$ Cohena\end{tabular}}}}}
\rput(6,9.8){\hyperlink{testy_normalnosci}{testy normalności}}
\rput(6,9.5){\hyperlink{testy_normalnosci}{rozkładu}}
\psline[linestyle=dotted]{<-}(3.4,11.2)(4,10)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgf9a4c59eca2e710fcb1307d27601e054.png)
Testy parametryczne
Współczynnik korelacji wewnątrzklasowej i test badający jego istotność
Współczynnik korelacji wewnątrzklasowej (ang. ICC - intraclass correlation coefficient) stosuje się w sytuacji, gdy pomiarów badanej zmiennej dokonuje kilku „sędziów” ( ). Mierzy on siłę sędziowskiej rzetelności, czyli stopień w jakim ich oceny są zgodne.
). Mierzy on siłę sędziowskiej rzetelności, czyli stopień w jakim ich oceny są zgodne.
Ponieważ można go wyznaczać w kilku różnych sytuacjach, rozróżnia się kilka jego odmian zależnych od modelu i typu zgodności. W zależności od występującej w danych zmienności możemy rozróżnić 2 główne modele badań i 2 typy zgodności.
Model 1
Dla każdego z losowo wybranych  ocenianych obiektów, wybierany jest losowo zestaw
ocenianych obiektów, wybierany jest losowo zestaw  sędziów z populacji sędziów. Przy czym dla każdego obiektu inny zestaw
sędziów z populacji sędziów. Przy czym dla każdego obiektu inny zestaw  sędziów może być wylosowany. Współczynnik ICC jest wówczas wyznaczany w modelu losowym ANOVA dla grup niezależnych. Na pytanie o rzetelność ocen pojedynczego sędziego odpowiada ICC(1,1) dany wzorem:
sędziów może być wylosowany. Współczynnik ICC jest wówczas wyznaczany w modelu losowym ANOVA dla grup niezależnych. Na pytanie o rzetelność ocen pojedynczego sędziego odpowiada ICC(1,1) dany wzorem:
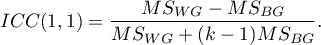
Do oszacowania wiarygodności wyników będących średnią ocen sędziowskich (dla  sędziów) wyznacza się ICC(1,k) dany wzorem:
sędziów) wyznacza się ICC(1,k) dany wzorem:
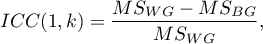
gdzie:
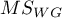 - średnia kwadratów wewnątrz grup,
- średnia kwadratów wewnątrz grup,
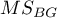 - średnia kwadratów między obiektami.
- średnia kwadratów między obiektami.
Model 2
Wybierany jest losowo zestaw  sędziów z populacji sędziów i każdy z nich ocenia wszystkie
sędziów z populacji sędziów i każdy z nich ocenia wszystkie  losowych obiektów.
Współczynnik ICC jest wówczas wyznaczany w modelu losowym ANOVA dla grup zależnych.
losowych obiektów.
Współczynnik ICC jest wówczas wyznaczany w modelu losowym ANOVA dla grup zależnych.
W zależności od poszukiwanego typu zgodności możemy szacować: zgodność bezwzględną tzn. jeśli sędziowie są zgodni bezwzględnie, to wydają dokładnie takie same oceny np. perfekcyjnie zgodne będą takie oceny wydane przez parę sędziów (2,2), (5,5), (8,8); lub spójność tzn. sędziowie mogą używać innych zakresów wartości ale poza tym przesunięciem nie powinno być różnic by zachować spójność werdyktu np. perfekcyjnie spójne będą takie oceny wydane przez parę sędziów (2,5), (5,8), (8,11).
- Zgodność bezwzględna
Na pytanie o rzetelność ocen pojedynczego sędziego odpowiada ICC(2,1) dany wzorem:
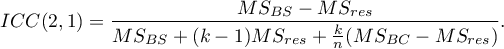
Do oszacowania wiarygodności wyników będących średnią ocen sędziowskich (dla  sędziów) wyznacza się ICC(2,k) dany wzorem:
sędziów) wyznacza się ICC(2,k) dany wzorem:
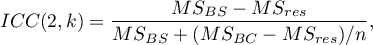
gdzie:
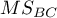 - średnia kwadratów między sędziami,
- średnia kwadratów między sędziami,
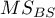 - średnia kwadratów między obiektami,
- średnia kwadratów między obiektami,
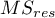 - średnia kwadratów dla reszt.
- średnia kwadratów dla reszt.
- Spójność
Na pytanie o rzetelność ocen pojedynczego sędziego odpowiada ICC(2,1) dany wzorem:
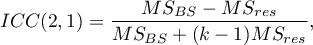
Do oszacowania wiarygodności wyników będących średnią ocen sędziowskich (dla  sędziów) wyznacza się ICC(2,k) dany wzorem:
sędziów) wyznacza się ICC(2,k) dany wzorem:
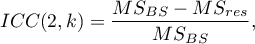
gdzie:
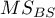 - średnia kwadratów między obiektami,
- średnia kwadratów między obiektami,
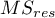 - średnia kwadratów dla reszt.
- średnia kwadratów dla reszt.
Uwaga!
Czasami istnieje konieczność rozważania modelu 3 1), tzn. wybierany jest zestaw  sędziów i każdy z nich ocenia wszystkie
sędziów i każdy z nich ocenia wszystkie  losowych obiektów. Wynik zgodności dotyczy tylko tych konkretnych
losowych obiektów. Wynik zgodności dotyczy tylko tych konkretnych  sędziów. Współczynnik ICC jest wówczas wyznaczany w modelu mieszanym (ponieważ losowość dotyczy tylko obiektów a nie dotyczy sędziów). Ponieważ ignorujemy zmienność dotyczącą sędziów, badamy spójność (a nie absolutną zgodność) i zastosowanie mogą mieć współczynniki z modelu drugiego: ICC(2,1) i ICC (2,k), gdyż są one tożsame z pożądanymi w tym przypadku współczynnikami ICC(3,1) i ICC (3,k) przy założeniu braku interakcji obiektów i sędziów.
sędziów. Współczynnik ICC jest wówczas wyznaczany w modelu mieszanym (ponieważ losowość dotyczy tylko obiektów a nie dotyczy sędziów). Ponieważ ignorujemy zmienność dotyczącą sędziów, badamy spójność (a nie absolutną zgodność) i zastosowanie mogą mieć współczynniki z modelu drugiego: ICC(2,1) i ICC (2,k), gdyż są one tożsame z pożądanymi w tym przypadku współczynnikami ICC(3,1) i ICC (3,k) przy założeniu braku interakcji obiektów i sędziów.
Uwaga!
Wartość 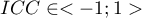 interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
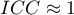 oznacza silną zgodność w ocenie poszczególnych obiektów przez sędziów, co ma odzwierciedlenie w dużej wariancji między obiektami (znacznej różnicy średnich między
oznacza silną zgodność w ocenie poszczególnych obiektów przez sędziów, co ma odzwierciedlenie w dużej wariancji między obiektami (znacznej różnicy średnich między  obiektami) i małej wariancji między ocenami sędziowskimi (niewielkiej różnicy średnich ocen wyznaczonych dla
obiektami) i małej wariancji między ocenami sędziowskimi (niewielkiej różnicy średnich ocen wyznaczonych dla  sędziów);
sędziów);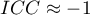 negatywny współczynnik korelacji wewnątrzklasowej, jest traktowany w ten sam sposób jak
negatywny współczynnik korelacji wewnątrzklasowej, jest traktowany w ten sam sposób jak 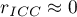 ;
;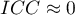 oznacza brak zgodności w ocenie poszczególnych obiektów przez sędziów, co ma odzwierciedlenie w małej wariancji między obiektami (niewielkiej różnicy średnich między
oznacza brak zgodności w ocenie poszczególnych obiektów przez sędziów, co ma odzwierciedlenie w małej wariancji między obiektami (niewielkiej różnicy średnich między  obiektami) i dużej wariancji między ocenami sędziowskimi (znaczącej różnicy średnich ocen wyznaczonych dla
obiektami) i dużej wariancji między ocenami sędziowskimi (znaczącej różnicy średnich ocen wyznaczonych dla  sędziów).
sędziów).
Test F do sprawdzania istotności współczynnika korelacji wewnątrzklasowej
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu dla wszystkich zmiennych będących różnicą par pomiarowych (lub normalność badanej zmiennej dla każdego pomiaru).
- dla modelu 1 - model niezależny, dla modelu 2 / 3 - model zależny.
Hipotezy:
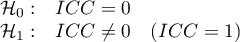
Statystyka testowa ma postać:
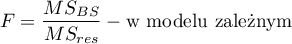
lub
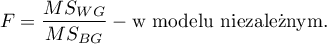
Statystyka ta podlega rozkładowi F Snedecora ze zdefiniowaną w modelu liczbą stopni swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji korelacji wewnątrzklasowej (ICC) wywołujemy poprzez menu Statystyka→Testy parametryczne→Korelacja wewnątrzklasowa (ICC) lub poprzez ''Kreator''.
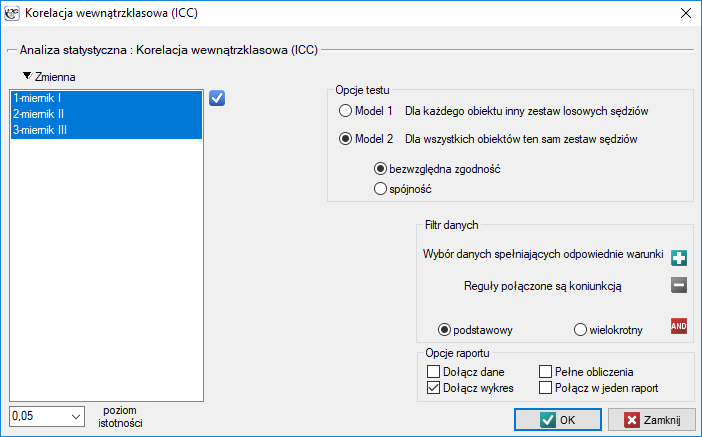
Przykład (plik natężenie dźwięku.pqs)
By skutecznie dbać o słuch pracowników zakładu pracy, w pierwszej kolejności należy rzetelnie oszacować natężenie dźwięku w poszczególnych miejscach przebywania osób. W pewnym zakładzie pracy postanowiono przed wyborem miernika natężenia dźwięku (sonografu) przeprowadzić eksperyment. Pomiarów natężenia dźwięku dokonano w 42 losowo wybranych na terenie zakładu punktach pomiarowych przy pomocy 3 wylosowanych sonografów analogowych i 3 losowo wybranych sonografów cyfrowych. Fragment zebranych pomiarów przedstawia poniższa tabela.
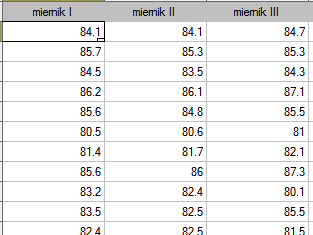
By sprawdzić który typ urządzenia (analogowy czy cyfrowy) lepiej zrealizuje postawione przed nim zadanie należy wyznaczyć współczynnik ICC w modelu 2 badając bezwzględną zgodność. Typ miernika o wyższym wskaźniku ICC będzie charakteryzował się bardziej wiarygodnymi pomiarami, przez co będzie w przyszłości wykorzystywany na terenie zakładu.
Analiza przeprowadzona dla mierników analogowych wskazuje na istotną zgodność pomiarów (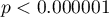 ). Rzetelność pomiaru dokonana miernikiem analogowym wynosi
). Rzetelność pomiaru dokonana miernikiem analogowym wynosi 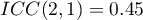 , natomiast rzetelność pomiaru będącego średnią pomiarów dokonanych przez 3 mierniki analogowe jest nieco wyższa i wynosi
, natomiast rzetelność pomiaru będącego średnią pomiarów dokonanych przez 3 mierniki analogowe jest nieco wyższa i wynosi 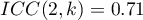 . Niepokojąco niska jest jednak dolna granica 95% przedziału ufności dla tych współczynników.
. Niepokojąco niska jest jednak dolna granica 95% przedziału ufności dla tych współczynników.
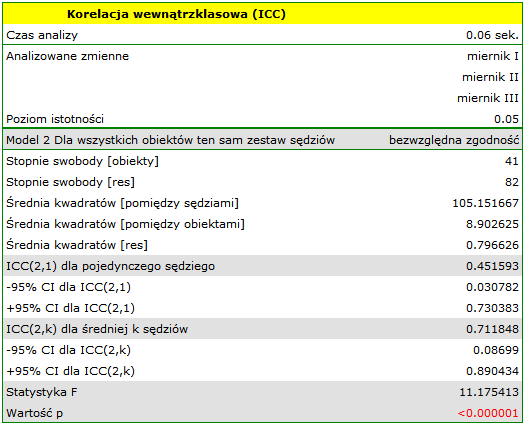
Podobna analiza przeprowadzona dla mierników cyfrowych dała lepsze rezultaty. Model ponownie jest istotny statystycznie, ale współczynniki ICC oraz ich przedziały ufności są znacznie wyżej niż dla mierników analogowych, a więc uzyskana zgodność bezwzględna jest wyższa 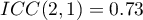 ,
, 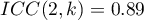 .
.
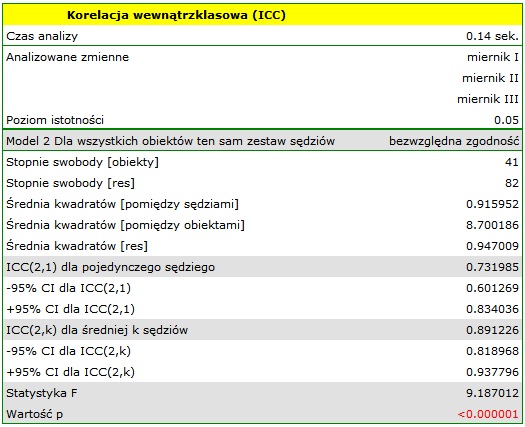
Dlatego ostatecznie w zakładzie pracy wykorzystywane będą mierniki cyfrowe.
Zgodność uzyskanych wyników dla mierników cyfrowych przedstawiono na wykresie punktowym, gdzie każdy punkt pomiarowy opisany jest wartością natężenia dźwięku uzyskaną dla poszczególnych mierników.
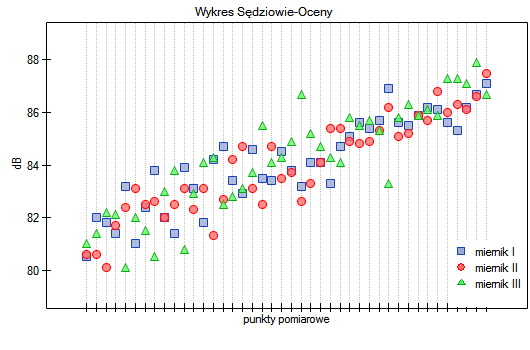
Przedstawiając wykres dla uprzednio posortowanych danych zgodnie ze średnią wartością natężenia dźwięku, można sprawdzić czy stopień zgodności rośnie lub spada wraz z wzrostem natężenia dźwięku. W przypadku naszych danych nieco wyższą zgodność (bliskość położenia punktów na wykresie) obserwować można przy wysokich wartościach natężenia dźwięku.
Podobnie, zgodność uzyskanych wyników obserwować można na wykresach Blanda-Altmana2) budowanych oddzielnie dla każdej pary mierników. Wykres dla miernika I i miernika II przedstawiono poniżej.
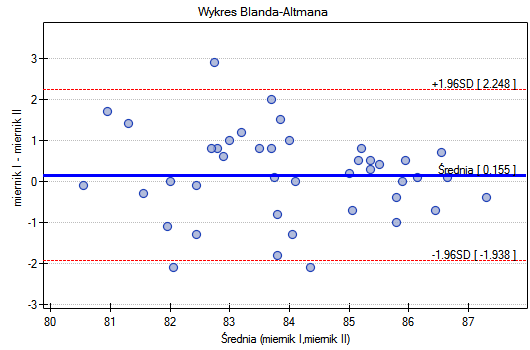
Tu również obserwujemy wyższą zgodność (punkty koncentrują się blisko osi poziomej y=0) dla wyższych wartości natężenia dźwięku.
Uwaga! Gdyby badaczowi nie zależało na oszacowaniu rzeczywistej wartości natężenia dźwięku na terenie zakładu, ale chciałby wskazać miejsca gdzie ten poziom jest wyższy niż w innych miejscach lub sprawdzić czy poziom hałasu zmienia się w czasie, wówczas wystarczającym modelem byłby model 2 badający spójność.
2014/08/22 20:00
2014/08/22 20:00
Testy nieparametryczne
Współczynnik Kappa Cohena i test badający jego istotność
Współczynnik Kappa Cohena (ang. Cohen's Kappa), Cohen J. (1960)3), określa stopień zgodności dwukrotnych pomiarów tej samej zmiennej w różnych warunkach. Pomiaru tej samej zmiennej może dokonać dwóch różnych sędziów (odtwarzalność) lub jeden sędzia może dokonać pomiaru dwukrotnie (powtarzalność). Współczynnik  wyznacza się dla zależnych zmiennych kategorialnych, a jego wartość zawiera się w przedziale od -1 do 1. Wartość 1 oznacza pełną zgodność, wartość 0 oznacza zgodność na poziomie takim samym jaki powstałby dla losowego rozłożenia danych w tabeli kontyngencji. Poziom pomiędzy 0 a -1 jest w praktyce niewykorzystywany. Ujemna wartość
wyznacza się dla zależnych zmiennych kategorialnych, a jego wartość zawiera się w przedziale od -1 do 1. Wartość 1 oznacza pełną zgodność, wartość 0 oznacza zgodność na poziomie takim samym jaki powstałby dla losowego rozłożenia danych w tabeli kontyngencji. Poziom pomiędzy 0 a -1 jest w praktyce niewykorzystywany. Ujemna wartość  oznacza zgodność na poziomie mniejszym niż powstała dla losowego rozłożenia danych w tabeli kontyngencji. Współczynnik
oznacza zgodność na poziomie mniejszym niż powstała dla losowego rozłożenia danych w tabeli kontyngencji. Współczynnik  można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach
można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach 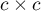 .
.
W zależności od potrzeb można wyznaczać Kappę nieważoną (czyli Kappę Cohena) lub Kappę ważoną. Przydzielane wagi (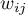 ) odnoszą się do poszczególnych komórek tabeli kontyngencji, na przekątnej wynoszą 1 a poza przekątną należą do przedziału
) odnoszą się do poszczególnych komórek tabeli kontyngencji, na przekątnej wynoszą 1 a poza przekątną należą do przedziału 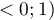 .
.
Kappa nieważona
Wyliczana jest dla danych, których kategorii nie da się uporządkować np. dane pochodzą od pacjentów, których dzielimy ze względu na rodzaj choroby jaka została zdiagnozowana, a chorób tych nie można uporządkować np. zapalenie płuc 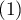 , zapalenie oskrzeli
, zapalenie oskrzeli 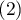 i inne
i inne 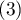 . W takiej sytuacji można sprawdzać zgodność diagnoz wystawionych przez dwóch lekarzy stosując nieważoną Kappę, czyli Kappę Cohena. Niezgodność par
. W takiej sytuacji można sprawdzać zgodność diagnoz wystawionych przez dwóch lekarzy stosując nieważoną Kappę, czyli Kappę Cohena. Niezgodność par 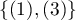 oraz
oraz 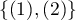 traktowana będzie równoważnie, a więc wagi poza przekątną macierzy wag będą zerowane.
traktowana będzie równoważnie, a więc wagi poza przekątną macierzy wag będą zerowane.
Kappa ważona
W sytuacji kiedy kategorie danych mogą być posortowane np. dane pochodzą od pacjentów, których dzielimy ze względu na stopień zmian chorobowych na: brak zmian 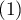 , zmiany łagodne
, zmiany łagodne 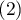 , podejrzenie raka
, podejrzenie raka 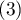 , rak
, rak 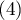 , budować można zgodność wystawionych ocen przez dwóch radiologów uwzględniając możliwość sortowania. Za bardziej niezgodne pary ocen mogą być wówczas uznane oceny
, budować można zgodność wystawionych ocen przez dwóch radiologów uwzględniając możliwość sortowania. Za bardziej niezgodne pary ocen mogą być wówczas uznane oceny 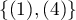 niż
niż 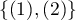 . By tak było, by kolejność kategorii wpływała na wynik zgodności, wyznaczać należy ważoną Kappę.
. By tak było, by kolejność kategorii wpływała na wynik zgodności, wyznaczać należy ważoną Kappę.
Przydzielane wagi mogą mieć postać liniową lub kwadratową.
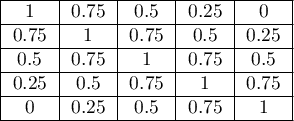
- Wagi liniowe (Cicchetti, 19714)) - wyliczane według wzoru:
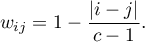
Czym większe oddalenie od przekątnej macierzy tym mniejsza waga, przy czym wagi maleją proporcjonalnie. Przykładowe wagi dla macierzy wielkości 5×5 przedstawia tabela:
- Wagi kwadratowe (Cohen, 19685)) - wyliczane według wzoru:
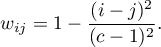
Czym większe oddalenie od przekątnej macierzy tym mniejsza waga, przy czym wagi maleją wolniej w bliższej odległości od przekątnej i szybciej w odległości dalszej. Przykładowe wagi dla macierzy wielkości 5×5 przedstawia tabela:
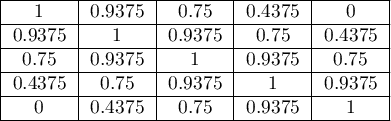
Wagi kwadratowe cieszą się większym zainteresowaniem ze względu na praktyczną interpretację współczynnika Kappa, który w tym przypadku tożsamy jest ze współczynnikiem korelacji wewnątrzklasowej 6).
By wyznaczyć zgodność współczynnikiem Kappa dane przedstawia się w postaci tabeli liczności obserwowanych 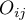 , dalej tą tabelę przekształca się w tabelę kontyngencji prawdopodobieństw
, dalej tą tabelę przekształca się w tabelę kontyngencji prawdopodobieństw 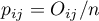 .
.
Współczynnik Kappa ( ) wyraża się wtedy wzorem:
) wyraża się wtedy wzorem:
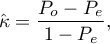
gdzie:
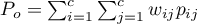 ,
,
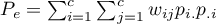 ,
,
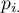 ,
, 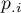 - sumy końcowe kolumn i wierszy tabeli kontyngencji prawdopodobieństw.
- sumy końcowe kolumn i wierszy tabeli kontyngencji prawdopodobieństw.
Uwaga!
 oznacza współczynnik zgodności w próbie, natomiast
oznacza współczynnik zgodności w próbie, natomiast 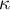 w populacji.
w populacji.
Błąd standardowy dla Kappa wyraża się wzorem:
![LaTeX \begin{displaymath}
SE_{\hat \kappa}=\frac{1}{(1-P_e)\sqrt{n}}\sqrt{\sum_{i=1}^{c}\sum_{j=1}^{c}p_{i.}p_{.j}[w_{ij}-(\overline{w}_{i.}+(\overline{w}_{.j})]^2-P_e^2}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img059555813b7a0927359f9000c829f6fe.png) gdzie:
gdzie:
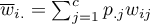 ,
,
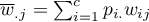 .
.
Test Z do sprawdzania istotności współczynnika Kappa Cohena ( ) (ang. The Z test of significance for the Cohen's Kappa) Fleiss (20037)) służy do weryfikacji hipotezy o zgodności wyników dwukrotnych pomiarów
) (ang. The Z test of significance for the Cohen's Kappa) Fleiss (20037)) służy do weryfikacji hipotezy o zgodności wyników dwukrotnych pomiarów 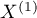 i
i 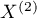 cechy
cechy  i opiera się na współczynniku
i opiera się na współczynniku  wyliczonym dla próby.
wyliczonym dla próby.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej (Kappa Cohena - nieważona) i skali porządkowej (Kappa ważona).
Hipotezy:
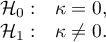
Statystyka testowa ma postać:
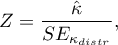
gdzie:
![LaTeX $\displaystyle{SE_{\kappa_{distr}}=\frac{1}{(1-P_e)\sqrt{n}}\sqrt{\sum_{i=1}^c\sum_{j=1}^c p_{ij}[w_{ij}-(\overline{w}_{i.}+\overline{w}_{.j})(1-\hat \kappa)]^2-[\hat \kappa-P_e(1-\hat \kappa)]^2}}$](/lib/exe/fetch.php?media=wiki:latex:/imgc30723ad5a68d25b44687da3bff2c069.png) .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji testu istotności Kappa-Cohena wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Kappa-Cohena lub poprzez Kreator.
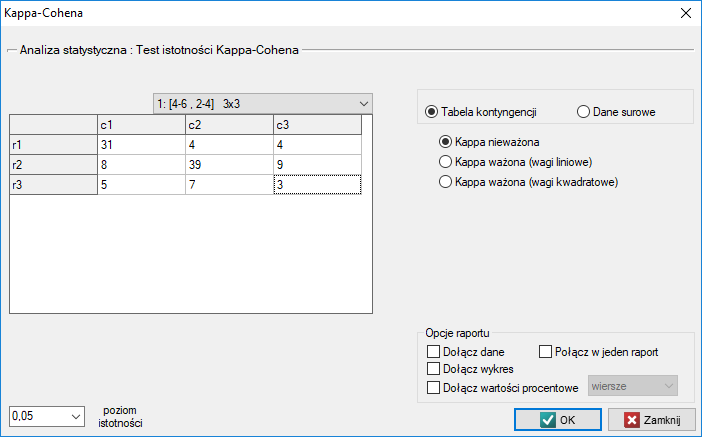
Badamy zgodność diagnozy postawionej przez 2 lekarzy. W tym celu pobieramy próbę 110 pacjentów szpitala dziecięcego. Lekarze przyjmują pacjentów w sąsiednich gabinetach. Każdy z pacjentów jest najpierw badany przez lekarza A a następnie przez lekarza B. Diagnozy postawione przez lekarzy przedstawia poniższa tabela.

Hipotezy:
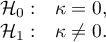
Moglibyśmy badać zgodność diagnozy poprzez zwykły procent wartości zgodnych. W naszym przykładzie zgodną diagnozę lekarze postawili dla 73 pacjentów (31+39+3=73) co stanowi 66.36% badanej grupy. Współczynnik Kappa wprowadza korekcję tej wartości o szanse na zgodność (tzn. w korekcji o tę zgodność, która pojawia się dla przypadkowego rozłożenia danych w tabeli).
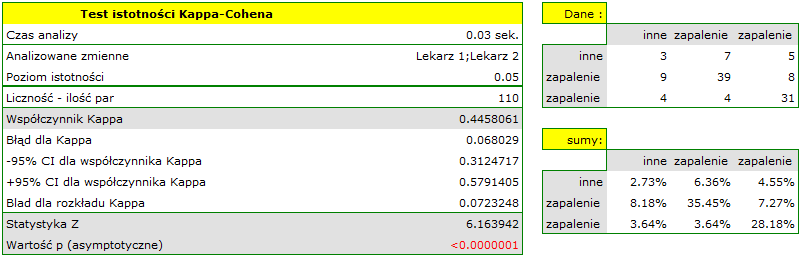
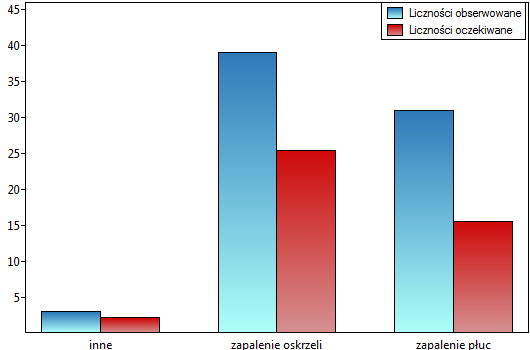
Zgodność wyrażona współczynnikiem 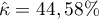 jest mniejsza niż ta nie skorygowana o szanse na zgodność.
jest mniejsza niż ta nie skorygowana o szanse na zgodność.
Wartość 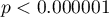 . Wynik taki, na poziomie istotności
. Wynik taki, na poziomie istotności  , świadczy o zgodności opinii tych 2 lekarzy.
, świadczy o zgodności opinii tych 2 lekarzy.
Przykład (plik radiologia.pqs)
W obrazie radiologicznym oceniano uszkodzenie wątroby w następujących kategoriach: brak zmian 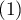 , zmiany łagodne
, zmiany łagodne  , podejrzenie raka
, podejrzenie raka  , rak
, rak  . Oceny dokonywało dwóch niezależnych radiologów bazując na grupie 70 pacjentów. Chcemy sprawdzić zgodność postawionej diagnozy.
. Oceny dokonywało dwóch niezależnych radiologów bazując na grupie 70 pacjentów. Chcemy sprawdzić zgodność postawionej diagnozy.
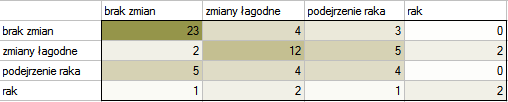
Hipotezy:
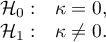
Ze względu na to, że diagnoza wystawiona jest na skali porządkowej, właściwą miarą zgodności byłby ważony współczynnik Kappa.

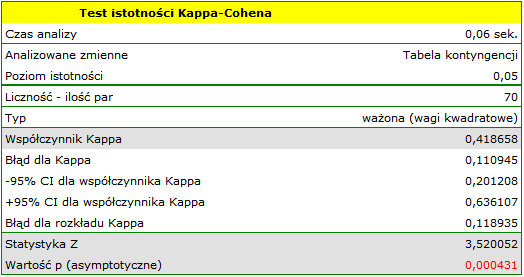
Ponieważ dane koncentrują się głównie na głównej przekątnej macierzy i w jej bliskim sąsiedztwie, współczynnik ważony wagami liniowymi jest niższy (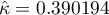 ) niż współczynnik wyznaczony dla wag kwadratowych (
) niż współczynnik wyznaczony dla wag kwadratowych (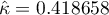 ). W obu sytuacjach jest to wynik istoty statystycznie (na poziomie istotności
). W obu sytuacjach jest to wynik istoty statystycznie (na poziomie istotności  ), wartość
), wartość  wynosi odpowiednio: 0.000007 i 0.000431.
wynosi odpowiednio: 0.000007 i 0.000431.
Gdyby w ocenach istniała duża niezgodność dotycząca dwóch skrajnych przypadków i para: (brak zmian i rak) znajdująca się w prawym górnym roku tabeli występowała zdecydowanie częściej, np. 15 razy, wówczas taki duży brak zgodności widoczny będzie bardziej, gdy wykorzystamy wagi kwadratowe (współczynnik Kappa drastycznie spadnie) niż przy wykorzystaniu wag liniowych.
2014/08/22 20:00
Współczynnik zgodności Kendalla i test badający jego istotność
Współczynnik zgodności 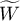 Kendalla (ang. Kendall's Coefficient of Concordance) opisany w pracy Kendalla i Babingtona-Smitha (1939)8) oraz Wallisa (1939)9) stosuje się w sytuacji, gdy dysponujemy rankingami pochodzącymi z różnych źródeł (od różnych sędziów) i dotyczącymi kilku (
Kendalla (ang. Kendall's Coefficient of Concordance) opisany w pracy Kendalla i Babingtona-Smitha (1939)8) oraz Wallisa (1939)9) stosuje się w sytuacji, gdy dysponujemy rankingami pochodzącymi z różnych źródeł (od różnych sędziów) i dotyczącymi kilku (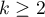 ) obiektów a zależy nam na ocenie zgodności tych rankingów. Często używa się go do mierzenia siły sędziowskiej rzetelności, czyli stopnia w jakim oceny sędziów są zgodne.
) obiektów a zależy nam na ocenie zgodności tych rankingów. Często używa się go do mierzenia siły sędziowskiej rzetelności, czyli stopnia w jakim oceny sędziów są zgodne.
Współczynnik zgodności Kendalla wyznacza się dla skali porządkowej lub interwałowej, a jego wartość wylicza się według wzoru:
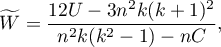
gdzie:
 - liczba różnych zbiorów ocen (ilość sędziów),
- liczba różnych zbiorów ocen (ilość sędziów),
 - liczba rangowanych obiektów,
- liczba rangowanych obiektów,
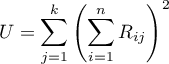 ,
,
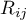 - rangi przypisane kolejnym obiektom
- rangi przypisane kolejnym obiektom  , oddzielnie dla każdego z sędziów
, oddzielnie dla każdego z sędziów 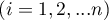 ,
,
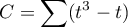 - korekta na rangi wiązane,
- korekta na rangi wiązane,
 - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Wzór na współczynnik zawiera poprawkę na rangi wiązane  . Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 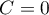 ).
).
Uwaga!
 oznacza współczynnik zgodności Kendalla w populacji, natomiast
oznacza współczynnik zgodności Kendalla w populacji, natomiast 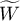 w próbie.
w próbie.
Wartość 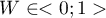 interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
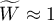 oznacza silną zgodność w ocenie poszczególnych obiektów przez sędziów;
oznacza silną zgodność w ocenie poszczególnych obiektów przez sędziów;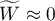 oznacza brak zgodności w ocenie poszczególnych obiektów przez sędziów.
oznacza brak zgodności w ocenie poszczególnych obiektów przez sędziów.
Współczynnik zgodności 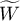 Kendalla a współczynnik
Kendalla a współczynnik 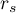 Spearmana:
Spearmana:
- Gdy wyliczymy wartość współczynnika korelacji Spearmana
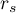 dla wszystkich możliwych par rankingów, to średni współczynnik
dla wszystkich możliwych par rankingów, to średni współczynnik 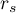 - oznaczony przez
- oznaczony przez 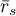 , jest funkcją liniową wartości współczynnika
, jest funkcją liniową wartości współczynnika 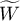 wyliczonego na podstawie tych danych:
wyliczonego na podstawie tych danych:
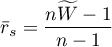
Współczynnik zgodności 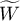 Kendalla a ANOVA Friedmana:
Kendalla a ANOVA Friedmana:
- Współczynnik zgodności
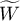 Kendalla i ANOVA Friedmana bazują na tym samym modelu matematycznym. W rezultacie wartość statystyki testowej testu chi-kwadrat do sprawdzania istotności współczynnika zgodności Kendalla i wartość statystyki testowej ANOVA Friedmana jest taka sama.
Kendalla i ANOVA Friedmana bazują na tym samym modelu matematycznym. W rezultacie wartość statystyki testowej testu chi-kwadrat do sprawdzania istotności współczynnika zgodności Kendalla i wartość statystyki testowej ANOVA Friedmana jest taka sama.
Test chi-kwadrat do sprawdzania istotności współczynnika zgodności Kendalla
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej.
Hipotezy:
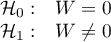
Statystyka testowa ma postać:
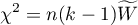
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyliczaną z wzoru: 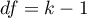 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji testu istotności W Kendalla wywołujemy poprzez menu Statystyka→Testy nieparametryczne→W Kendalla lub poprzez ''Kreator''.
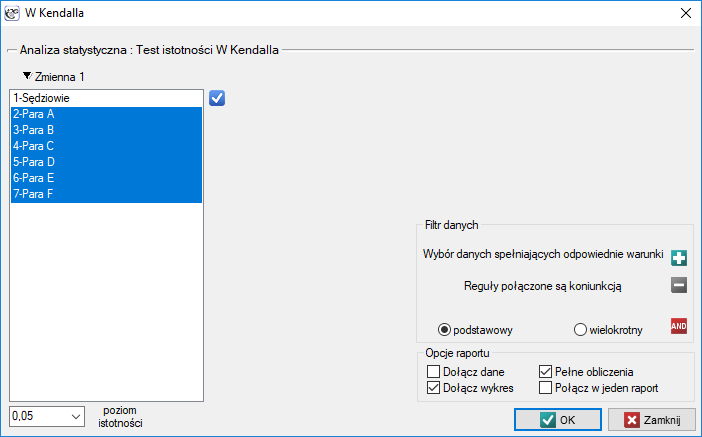
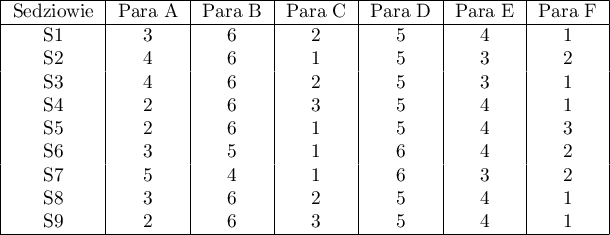
W systemie szóstkowym oceny par tanecznych 9 sędziów punktuje m.in. wrażenie artystyczne. Sędziowie rozpoczynają wystawianie oceny od porównania zawodników względem siebie i ustawienia ich na określonym miejscu (tworzą ich ranking). Sprawdzimy, czy rangi przypisane przez sędziów są zgodne:
Hipotezy:

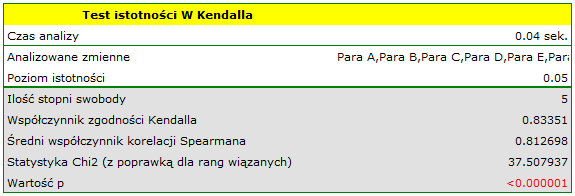
Porównując wartość 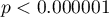 z poziomem istotności
z poziomem istotności  , stwierdziliśmy, że oceny sędziów są statystycznie zgodne. Siła tej zgodności jest wysoka i wynosi
, stwierdziliśmy, że oceny sędziów są statystycznie zgodne. Siła tej zgodności jest wysoka i wynosi 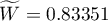 , podobnie jak średni współczynnik korelacji monotonicznej Spearmana
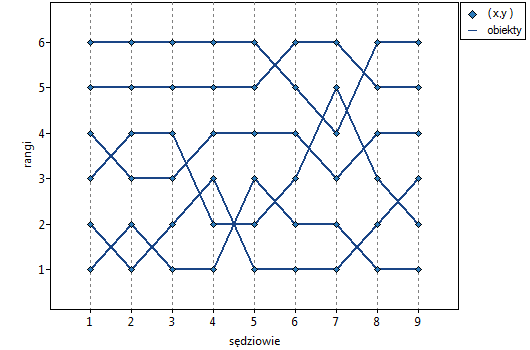
, podobnie jak średni współczynnik korelacji monotonicznej Spearmana 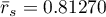 . Wynik ten możemy przedstawić na wykresie, na którym oś X reprezentuje kolejnych sędziów. Wówczas im częściej przecinają się linie, (które powinny być równoległe do osi X, gdy zgodność jest pełna), tym słabszą zgodność reprezentują oceny sędziów.
. Wynik ten możemy przedstawić na wykresie, na którym oś X reprezentuje kolejnych sędziów. Wówczas im częściej przecinają się linie, (które powinny być równoległe do osi X, gdy zgodność jest pełna), tym słabszą zgodność reprezentują oceny sędziów.
2014/08/22 20:00
Współczynnik Kappa Fleissa i test badający jego istotność
Współczynnik ten określa zgodność pomiarów prowadzonych przez kliku sędziów (Fleiss, 197110)) i jest rozszerzeniem współczynnika Kappa Cohena, pozwalającego na badanie zgodności jedynie dwóch sędziów. Przy czym, należy zaznaczyć że każdy z  losowo wybranych obiektów może być oceniany przez inny losowy zestaw
losowo wybranych obiektów może być oceniany przez inny losowy zestaw  sędziów. Analiza opiera się na danych przekształconych do tabeli o
sędziów. Analiza opiera się na danych przekształconych do tabeli o  wierszach i
wierszach i  kolumnach, gdzie
kolumnach, gdzie  stanowi liczbę możliwych kategorii, do których sędziowie przydzielają badane obiekty. Zatem w każdym wierszu tabeli podano
stanowi liczbę możliwych kategorii, do których sędziowie przydzielają badane obiekty. Zatem w każdym wierszu tabeli podano 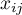 czyli liczbę sędziów wydających określone w danej kolumnie opinie.
czyli liczbę sędziów wydających określone w danej kolumnie opinie.
Współczynnik Kappa ( ) wyraża się wtedy wzorem:
) wyraża się wtedy wzorem:
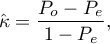
gdzie:
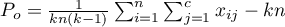 ,
,
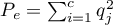 ,
,
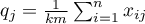 .
.
Wartość 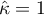 oznacza pełną zgodność sędziów, natomiast
oznacza pełną zgodność sędziów, natomiast 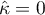 oznacza zgodność jaka powstałaby, gdyby opinie sędziów wydane były w sposób losowy. Wartości ujemne Kappa wskazują natomiast na zgodność mniejszą niż na poziomie losowym.
oznacza zgodność jaka powstałaby, gdyby opinie sędziów wydane były w sposób losowy. Wartości ujemne Kappa wskazują natomiast na zgodność mniejszą niż na poziomie losowym.
Dla współczynnika  można wyznaczyć błąd standardowy
można wyznaczyć błąd standardowy 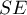 , który pozwala na zbadanie istotności statystycznej i wyznaczenie asymptotycznych przedziałów ufności.
, który pozwala na zbadanie istotności statystycznej i wyznaczenie asymptotycznych przedziałów ufności.
Test Z do sprawdzania istotności współczynnika Kappa Fleissa ( ) (ang. The Z test of significance for the Fleiss's Kappa) Fleiss (200311)) służy do weryfikacji hipotezy o zgodności ocen kilku sędziów i opiera się na współczynniku
) (ang. The Z test of significance for the Fleiss's Kappa) Fleiss (200311)) służy do weryfikacji hipotezy o zgodności ocen kilku sędziów i opiera się na współczynniku  wyliczonym dla próby.
wyliczonym dla próby.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę.
Hipotezy:
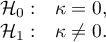
Statystyka testowa ma postać:
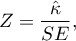
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga! Wyznaczanie współczynnika Kappa Fleissa zbliżone jest koncepcyjnie do metody Mantela-Haenszela. Wyznaczona Kappa jest ogólną miarą podsumowującą zgodność wszystkich ocen sędziowskich i może być wyznaczona jako Kappa utworzona z poszczególnych warstw, którymi są konkretne oceny sędziowskie (Fleiss, 200312)). Dlatego, jako podsumowanie każdej warstwy można wyznaczyć zgodność sędziowską (współczynnik Kappa) podsumowującą każdą możliwą ocenę z osobna.
Okno z ustawieniami opcji testu istotności Kappa-Fleissa wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Kappa-Fleissa
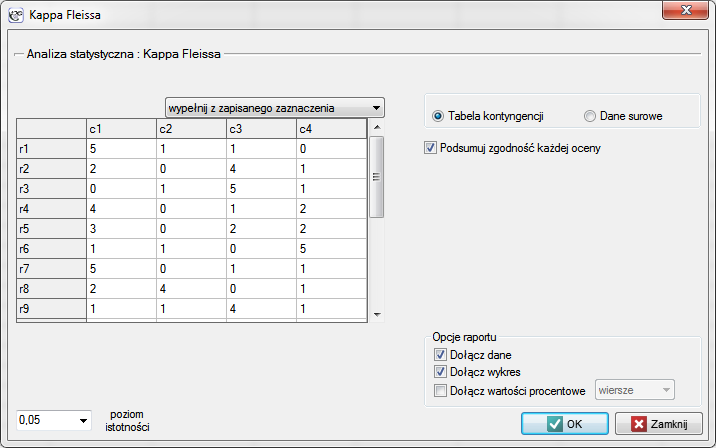
Przykład (plik temperament.pqs)
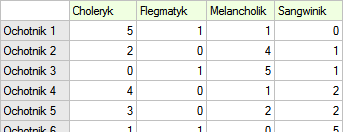
20 ochotników bierze udział w zabawie mającej na celu ustalenie typu osobowości badanych. Każdy z ochotników dysponuje oceną wystawioną przez 7 różnych obserwatorów (najczęściej osób z bliskiego otoczenia lub rodziny). Każdy z obserwatorów został zapoznany z podstawowymi cechami opisującymi temperament w poszczególnych typach osobowości: choleryk, flegmatyk, melancholik, sangwinik. Badamy zgodność obserwatorów w przypisywaniu typów osobowości. Fragment danych przedstawia poniższa tabela.
Hipotezy:

Obserwujemy nieduży współczynnik Kappa = 0.244918, lecz istotny statystycznie (p<0.000001), co oznacza nieprzypadkową zgodność ocen sędziowskich. Istotna zgodność dotyczy każdej oceny, czego potwierdzeniem jest raport podsumowujący zgodność dla każdej warstwy (dla każdej oceny) oraz wykres prezentujący poszczególne współczynniki Kappa i Kappę podsumowującą całość.
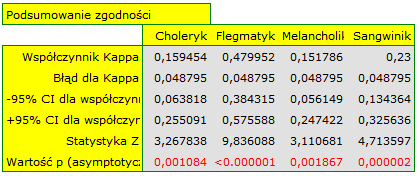
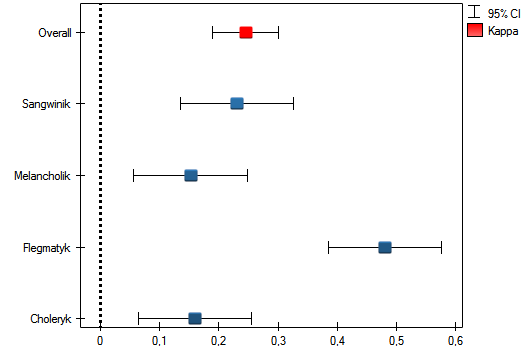
Ciekawy może być fakt, że najwyższa zgodność dotyczy oceny flegmatyków (Kappa=0.479952).
Przy niewielkiej liczbie obserwowanych osób warto również wykonać wykres obrazujący w jaki sposób obserwatorzy oceniali każdą z nich.
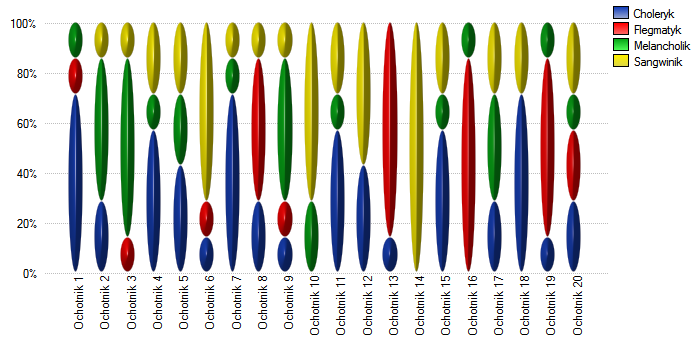
W tym przypadku tylko osoba nr 14 uzyskała jednoznaczną ocenę typu osobowości - sangwinik. Osoby nr 13 i 16 ocenione były jako typ flegmatyk przez 6 obserwatorów (na 7 możliwych). W przypadku pozostałych osób panowała nieco mniejsza zgodność ocen. Najtrudniejszy do zdefiniowania typ osobowości wydaje się cechować ostatnią osobę, która uzyskała najbardziej różnorodny zestaw ocen.
2015/12/27 23:42
· admin
2014/08/22 20:00
1)
Shrout P.E., and Fleiss J.L (1979), Intraclass correlations: uses in assessing rater reliability. Psychological Bulletin, 86, 420-428
2)
Bland J.M., Altman D.G. (1999), Measuring agreement in method comparison studies. Statistical Methods in Medical Research 8:135-160.
3)
Cohen J. (1960), A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 10,3746
4)
Cicchetti D. and Allison T. (1971), A new procedure for assessing reliability of scoring eeg sleep recordings. American Journal EEG Technology, 11, 101-109
5)
Cohen J. (1968), Weighted kappa: nominal scale agreement with provision for scaled disagreement or partial credit. Psychological Bulletin, 70, 213-220
6)
Fleiss J.L., Cohen J. (1973), The equivalence of weighted kappa and the intraclass correlation coeffcient as measure of reliability. Educational and Psychological Measurement, 33, 613-619
7)
, 11)
, 12)
Fleiss J.L., Levin B., Paik M.C. (2003), Statistical methods for rates and proportions. 3rd ed. (New York: John Wiley) 598-626
8)
Kendall M.G., Babington-Smith B. (1939), The problem of m rankings. Annals of Mathematical Statistics, 10, 275-287
9)
Wallis W.A. (1939), The correlation ratio for ranked data. Journal of the American Statistical Association, 34,533-538
10)
Fleiss J.L. (1971), Measuring nominal scale agreement among many raters. Psychological Bulletin, 76 (5): 378–382
statpqpl/zgodnpl.txt · ostatnio zmienione: 2019/12/17 17:30 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


