Narzędzia użytkownika

Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Obsługa programu » Praca z arkuszami danych » Transformacja
Ślad: • Transformacja

Transformacja

Okno transformacji danych wywołujemy poprzez Dane→Transformuj…

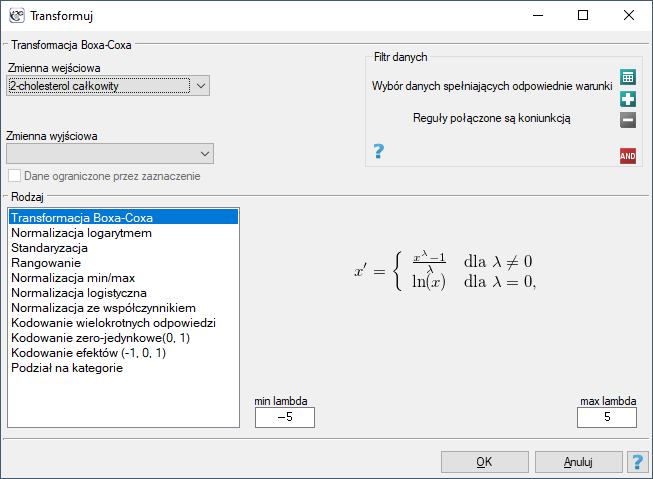
Transformacja danych to ich przekształcenie w taki sposób, by spełniały określone kryteria np. spełniały kryteria normalności rozkładu czy też rozciągały się w określonym przedziale.

  • Transformacja Boxa-Coxa
    Transformacja Boxa-Coxa wprowadzona przez Boxa i Coxa w roku 19641) sprowadza dane do rozkładu normalnego poprzez przekształcenie oparte na współczynniku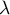 $\lambda$. Do przeprowadzenia transformacji wymagane są dane dodatnie. Jeśli dane nie są dodatnie zaleca się ich wcześniejsze przekształcenie do liczb dodatnich metodą normalizacji min-max.

Transformacja Boxa-Coxa wyraża się wzorem:
\begin{displaymath} x'=\left\{ \begin{array}{cl} \frac{x^\lambda-1}{\lambda} & $dla $ \lambda \neq 0\\ \ln(x) & $dla $\lambda = 0, \end{array}\right. \end{displaymath}

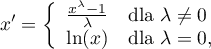
gdzie wartość 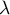$\lambda$ wyznaczana jest jako maksymalna wartość logartmu funkcji wiarygodności (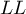$LL$) w podanym przez badacza przedziale. Domyślny przedział dla poszukiwania wartości 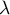$\lambda$ to przedział [-5, 5], a funkcja 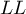$LL$ opisana jest wzorem:

\begin{displaymath} LL=-\frac{n}{2}\ln(sd_{pop}^2)+(\lambda -1)\sum\ln x \end{displaymath}

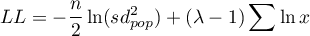
gdzie:
$n$ - liczność próby,
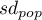$sd_{pop}$ - odchylenie standardowe populacji.

Uwaga! Jeśli przed transformacją Boxa-Coxa wykorzystano normalizację min-max, wówczas po transformacji Boxa-Coxa można powrócić do poprzedniego przedziału ponownie używając tej transformacji.

  • Transformacja logarytmiczna
    Transformacja logarytmiczna może być wykorzystywana do redukcji skośności rozkładu tzn. w sytuacji gdy mamy do czynienia z rozkładem lognormalnym.
    \begin{displaymath} x'=\ln x \end{displaymath}
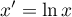
  • Standaryzacja
    Standaryzacja, to przekształcenie danych, w wyniku którego zmienna uzyskuje średnią równą 0 a odchylenie standardowe równe 1.
    \begin{displaymath} x'=\frac{x-\bar{x}}{sd} \end{displaymath}
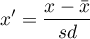
  • Rangowanie

Rangi - są to kolejne liczby (zwykle naturalne) przypisane do wartości uporządkowanych pomiarów badanej zmiennej. Często wykorzystywane są w tych testach nieparametrycznych, które bazują wyłącznie na kolejności elementów w próbie. Przypisanie do zmiennej wyliczonych według niej rang zwane jest rangowaniem. Rangowanie może odbywać się dla zmiennych sortowanych rosnąco (jest to domyślne ustawienie) lub malejąco.

Powtarzającym się wartościom zmiennej przypisuje się rangę wiązaną. Rangą wiązaną może być:
- średnia arytmetyczna wyliczana z proponowanych dla powtarzanych wartości kolejnych liczb naturalnych - jest to domyślne ustawienie;
- dolna granica, czyli najmniejsza z proponowanych dla powtarzanych wartości kolejnych liczb naturalnych;
- górna granica, czyli największa z proponowanych dla powtarzanych wartości kolejnych liczb naturalnych. ;. Taka ranga nazywana jest rangą wiązaną.

Na przykład dla zmiennej o następujących wartościach: 8.6, 5.3, 8.6, 7.1, 9.3, 7.2, 7.3, 7.4, 7.3, 5.2, 7, 9.9, 8.6, 5.7 przypisywane są następujące rangi:

\begin{tabular}{|c|c|} \hline posortowane wartości zmiennej &rangi\\\hline 5.2 &1 \\ 5.3 &2 \\ 5.7 &3 \\ 7 &4 \\ 7.1 &5 \\ 7.2 &6 \\ 7.3 &7.5 \\ 7.3 &7.5 \\ 7.4 &9 \\ 8.6 &11 \\ 8.6 &11 \\ 8.6 &11 \\ 9.3 &13 \\ 9.9 &14 \\ \hline \end{tabular}

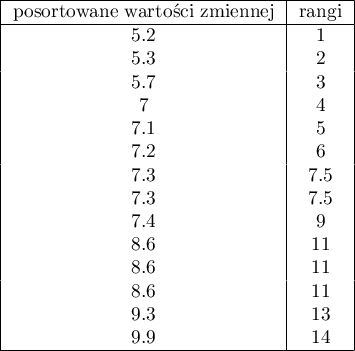
Przy czym dla zmiennej o wartości 7.3 przypisana jest ranga wiązana wyliczona z liczb: 7 i 8, a dla zmiennej o wartości 8.6 ranga wiązana wyliczona z liczb: 10, 11, 12.

  • Normalizacja min-max
    Normalizacja min-max przy pomocy funkcji liniowej sprowadza dane do wskazanego przez użytkownika przedziału (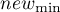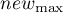$new_{\min}$, $new_{\max}$). Powinniśmy przy tym znać zakres jaki mogą osiągnąć dane. Jeśli nie znamy tego zakresu, możemy posłużyć się wartością największą i najmniejszą występującą w analizowanym zbiorze (w oknie Transformacji zaznaczamy wtedy opcję oblicz z próby).
    \begin{displaymath} x'=\frac{x-\min}{\max-\min}\cdot(new_{\max}-new_{\min})+new_{\min} \end{displaymath}
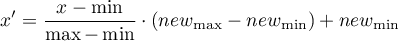
  • Normalizacja S-kształtna
    Normalizacja przy pomocy funkcji logarytmicznej (S-kształtnej) sprowadza dane zestandaryzowane do wskazanego przedziału.
    \begin{displaymath} x'=\frac{e^x}{1-e^x} \end{displaymath}
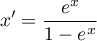
    Jeśli tak przekształcone dane chcemy rozciągnąć na innym przedziale niż zadany, wówczas w oknie Transformacji należy wprowadzić zakres nowego przedziału.
  • Funkcja normalizująca ze współczynnikiem
    Normalizacja ta sprowadza dane zestandaryzowane do wskazanego przedziału przy pomocy funkcji S-kształtnej o zmieniającym się współczynniku normalizacji $\alpha$.
    \begin{displaymath} x'=\frac{x}{\sqrt{x^2+\alpha}} \end{displaymath}
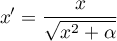
    Zwiększenie wartości współczynnika $\alpha$ tworzy wykres o bardziej łagodnym zboczu.
    Jeśli tak przekształcone dane chcemy rozciągnąć na innym przedziale niż zadany, wówczas w oknie Transformacji należy wprowadzić zakres nowego przedziału.
  • Kodowanie wielokrotnych odpowiedzi
    Ten rodzaj kodowania pozwala przygotować odpowiedzi udzielone na pytania wielokrotnego wyboru w taki sposób, by ułatwić ich dalszą obróbkę statystyczną. W efekcie zastosowania tej transformacji wybrana zmienna o k- możliwościach odpowiedziach jest rozbijana na k nowych zmiennych. Przy czym należy podać jaki znak (lub zestwa znaków) jest separatorem poszczególnych kategorii. Np. Zapytano ankietowanych jaki alkohol piją? Dane zapisano w kolumnie Alkohol oddzielając wielokrotne odpowiedzi znakiem średnika. Taki zapis danych nie pozwala nawet na proste podsumowanie. Nie można między innymi szybko zliczyć ile osób pije wino. Po przekodowaniu wielokrotnych odpowiedzi uzyskano trzy nowe kolumny - po jednej dla każdej z możliwych odpowiedzi. Każdą z tych kolumn można teraz poddać analizie statystycznej.

\begin{tabular}{|c|c|c|c|} \hline Alkohol &Alkohol(piwo) &Alkohol(wino) & Alkohol(wódka)\\\hline piwo;wino &1 &1 &0 \\ wino &0 &1 &0 \\ wino &0 &1 &0 \\ piwo &1 &0 &0 \\ wódka;wino &0 &1 &1 \\ wino;wódka &0 &1 &1 \\ piwo;wódka &1 &0 &1 \\ piwo;wino;wódka &1 &1 &1 \\ \hline \end{tabular}

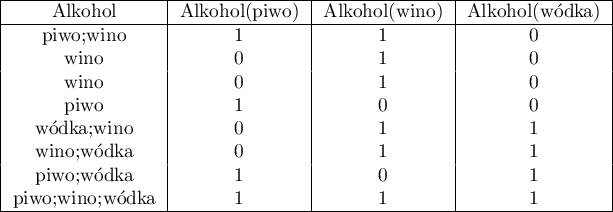
  • Kodowanie zero-jedynkowe
    Transformacja zmiennej o $k$ kategoriach poprzez kodowanie zero-jedynkowe pozwala na uzyskanie 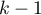$k-1$ zmiennych fikcyjnych. Taka forma przekształcania wykorzystywana jest przede wszystkim w modelach regresji. Dokładny opis tego typu transformacji można znaleźć w dziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
  • Kodowanie efektów
    Transformacja zmiennej o $k$ kategoriach poprzez kodowanie efektów pozwala na uzyskanie 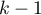$k-1$ zmiennych fikcyjnych. Taka forma przekształcania wykorzystywana jest przede wszystkim w modelach regresji i ANOVA. Dokładny opis tego typu transformacji można znaleźć w dziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
  • Podział na kategorie

    Taki sposób przygotowania danych pozwala na dowolny podział zmiennych np. cholesterol całkowity możemy podzielić zgodnie z obowiązującymi normami (wówczas wybieramy podział Ręczny, ustawiamy liczbę kategorii i sami wpisujemy ich granice oraz nadajemy odpowiednie etykiety dla każdej kategorii). Jeśli jednak nie mamy gotowego pomysłu na podział naszych danych można skorzystać z zaproponowanych w oknie opcji podziału automatycznego. Możliwe sposoby podziału zmiennej:

    - Naturalny Podział (Jenks) - metoda polegająca na takim podziale zmiennej na klasy, by zminimalizować wariancję w klasach a zmaksymalizować wariancję pomiędzy klasami.

    - Podział według kwantyli - metoda polegająca na podziale zmiennej na klasy równej liczności.

    - Odchylenie standardowe - metoda polegająca na podziale zmiennej na klasy w oparciu o oddalenie od średniej o 1, 2 lub więcej odchyleń standardowych.

    - Błąd standardowy średniej - metoda polegająca na podziale zmiennej na klasy w oparciu o oddalenie od średniej o 1, 2 lub więcej błędów standardowych średniej.

    - Ręczny - metoda polegająca na podziale zmiennej na klasy wg dowolnego podziału wprowadzonego ręcznie przez badacza.

    W oknie podziału możliwe jest również wybranie opcji Dodaj schemat kolorów wówczas kolumna, która będzie przechowywała nowe dane zostanie oznaczona kolorami zgodnie ze wskazanym schematem

Zadanie (plik: normalizacja.pqs)

Dokonaj przekształcenia wszystkich zmiennych zawartych w pliku

a) Przekształć wartość trójglicerydów poprzez transformację Boxa-Coxa a następnie sprawdź przy pomocy odpowiedniego testu, czy dane te mają rozkład normalny.
b) Przekształć wartość trójglicerydów poprzez transformację logarytmiczną a następnie sprawdź przy pomocy odpowiedniego testu, czy dane te mają rozkład normalny.
c) Stosując normalizację min-max przekształć wybrane zmienne do przedziału [0,10].
d) Stosując normalizację S-kształtną przekształć wybrane zmienne do zadanego przez siebie przedziału.
e) Stosując normalizację ze współczynnikiem przekształć wybrane zmienne do zadanego przez siebie przedziału. Zrób to kilkukrotnie zmieniając wartość współczynnika $\alpha$.
f) Dokonaj standaryzacji wszystkich danych, które są opisane rozkładem normalnym.
g) Przekształć zmienną obrazującą jak zmieniła się masa ciała podczas stosowania diety tak, by przedstawiała ona rozkład normalny.
h) Pytanie o przebytych chorobach zakaźnych było pytaniem wielokrotnego wyboru. Przygotuj uzyskane odpowiedzi na to pytanie tak, by można było poddać je dalszej obróbce statystycznej tzn. zapisz każdą z wielokrotnych odpowiedzi w innej kolumnie.
i) Przygotuj zmienną wykształcenie tak, by była zapisana przy pomocy zmiennych fikcyjnych o kodowaniu zero-jedynkowym.
j) Przygotuj zmienną cholesterol całkowity dzieląc ją na 3 klasy wg podziału na percentyle (kwartyle). Powstałym klasom nadaj etykiety :„niski”, „przeciętny”, „wysoki” i dobierz schemat kolorów.

1)
Box G. E. , Cox D. R. (1964), An analysis of transformations. Journal of the Royal Statistical Society, Series B 26: 211–252

Narzędzia strony

Narzędzia witryny