Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
przestrzenpl:wsteppl
Spis treści
Analiza przestrzenna - wstęp
Podstawowe definicje
System Informacji Geograficznej - GIS (ang. Geographic Information System) - jest systemem służącym do wprowadzania, gromadzenia, przetwarzania oraz wizualizacji danych geograficznych. Z technicznego punktu widzenia jest to narzędzie, które pozwala na analizę powiązanych ze sobą:
- informacji o lokalizacji przestrzennej obiektów - reprezentowanej za pomocą mapy;
- charakterystyki opisowej dotyczącej prezentowanych na mapie obiektów - reprezentowanej za pomocą bazy danych.
Obiekty prezentowane za pomocą mapy to:
- Punkty - których lokalizację w przestrzeni 2D definiujemy poprzez dwie współrzędne
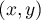 ;
; - Wielopunkty - to punkty pogrupowane w zbiory:
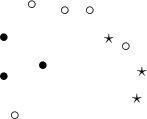
Przykład wielopunktu, w którym dla każdego punktu zdefiniowana jest jego przynależność do jednej z 3 grup.
- Linie - powstają przez połączenie w odpowiednim porządku kolejnych punktów (linie mogą się przecinać);
- Wielokąty - to zamknięte powierzchnie ograniczone przez zewnętrzne pierścienie (zamknięte, nie przecinające się linie przechodzące w określonej kolejności przez co najmniej 3 różne punkty). Wielokąty mogą zawierać również wewnętrzne pierścienie stanowiące ich granicę wewnętrzną. Przy czym pierścienie zewnętrzne definiowane są zgodnie z ruchem wskazówek zegara a pierścienie wewnętrzne odwrotnie.
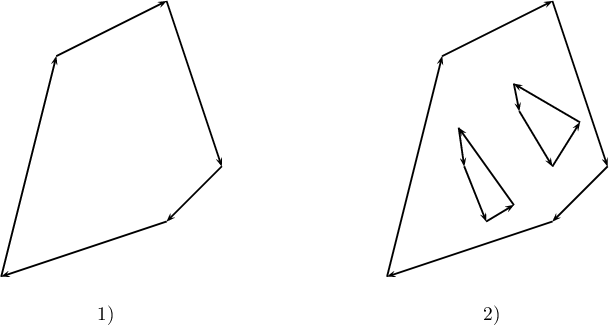
1)Przykład wielokąta posiadającego tylko granicę zewnętrzną (bez pierścieni wewnętrznych);
2)Przykład wielokąta posiadającego granice zewnętrzną i granice wewnętrzne (obszary zaznaczone przez pierścienie wewnętrzne stanowią część zewnętrznej powierzchni, czyli nie należą do wielokąta).
Atrybuty obiektów zapisane są w bazie za pomocą:
liczb - np. powierzchnia, temperatura,
tekstów - np. nazwy obiektów.
Projekcja mapy jest matematycznym sposobem odwzorowania powierzchni kuli ziemskiej na płaszczyznę. Istnieje szereg metod takiego odwzorowania. Odwzorowania mogą bazować na elipsoidzie obrotowej lub powierzchni kuli (sfera) bądź ich części.
Każde odwzorowanie jest bazą do zdefiniowania odpowiedniego układu współrzędnych. Ponieważ każda projekcja powierzchni niesie ze sobą pewne zniekształcenia (zniekształcenia kątów, pól, długości), wybór odpowiedniego układu uzależniony jest od celu do jakiego będzie użyta mapa.
Układy współrzędnych stosowane w kartografii dzielimy na:
- układy współrzędnych geograficznych (określają szerokość i długość geograficzną);
- układy współrzędnych prostokątnych płaskich (tożsame z układem kartezjańskim);
- układy współrzędnych biegunowych.
Aby mapa została poprawnie wczytana, program PQStat wymaga wektorowej mapy zapisanej w pliku SHAPEFILE (shp) zdefiniowanej w odpowiednim układzie współrzędnych prostokątnych płaskich, wymagana miara liniowa.
Program stara się automatycznie wykrywać mapy zawierające współrzędne geograficzne. Jeżeli podczas importu mapy program wykryje układ współrzędnych geograficznych, zaproponowana zostanie konwersja współrzędnych do układu UTM (Universal Transverse Mercator) bazując na układzie odniesienia WGS-84. Ze względu na możliwość uzyskania błędnej konwersji (na skutek stosowania wielu układów współrzędnych geograficznych i braku pewności co do zastosowanego układu), zalecane jest używanie map odpowiednio już przygotowanych - w układzie współrzędnych prostokątnych płaskich.
2014/08/24 23:53
· admin
Wczytywanie map
Mapa wraz z przypisaną do niej bazą atrybutów może być wczytana poprzez:
- import pliku kształtów SHP do arkusza danych,
- wczytanie pliku PQS/PQX zawierającego dane z plików kształtów SHP.
Import pliku kształtów SHP
Importu dokonujemy wybierając z menu Plik→Importuj dane …→SHP/SHX/DBF ESRI Shapefile (*.shp).
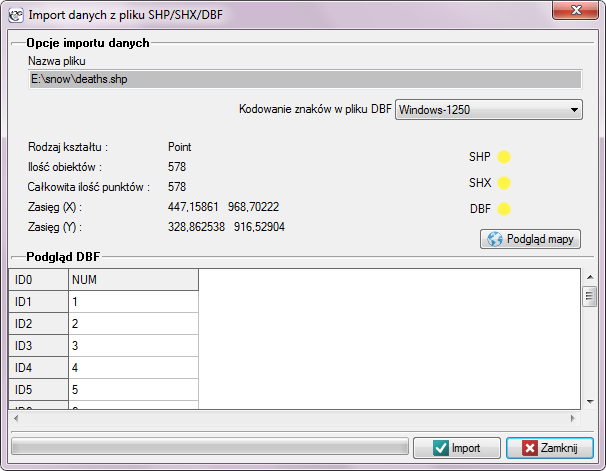
W oknie importu mamy możliwość podglądu importowanej mapy oraz jej atrybutów zapisanych w pliku DBF. Jeśli w katalogu, z którego dokonujemy importu znajdują się wszystkie pliki potrzebne do wczytania mapy, wówczas odpowiednie kontrolki sygnalizują kolorem żółtym poprawność odczytu odpowiednich plików. Atrybuty przypisane do pliku kształtów w formie bazy danych DBF nie są wymagane do poprawnego wczytania mapy, tabela atrybutów może zostać uzupełniona po wczytaniu pliku mapy poprzez wypełnienie odpowiednich komórek arkusza powiązanego z mapą.
2014/08/24 23:52
· admin
Ograniczenie obszaru roboczego
Ograniczenie obszaru roboczego wykonuje się w celu wskazania tylko tych obiektów, których ma dotyczyć analiza. W programie obiekty takie wskazuje się poprzez ich aktywację lub dezaktywację. Obiekty nieaktywne nie biorą udziału w analizach statystycznych.
Ręczna aktywacja/dezaktywacja obiektów
- Wskazanie wiersza w arkuszu danych opisującego odpowiedni obiekt i wybranie opcji
Aktywuj/Dezaktywujz menu kontekstowego na jego nazwie; - Wskazanie obiektu na mapie i wybranie z menu kontekstowego
Aktywuj/DezaktywujlubIdentyfikuj→Aktywuj/Dezaktywuj obiekt.
Automatyczna aktywacja/dezaktywacja obiektów
- Selekcja obiektów na podstawie arkusza danych – przykładowo, można wskazać jako aktywne tylko te sklepy, które są sklepami spożywczymi o powierzchni nie większej niż 1000m2. Ustawienie odpowiednich warunków selekcji obiektów odbywa się wówczas w oknie
Aktywacji/Dezaktywacjidostępnego po wybraniu menuEdycja→Aktywuj/Dezaktywuj (filtr)…. Szczegółowy opis sposobów tego typu selekcji można znaleźć w Podręczniku Użytkownika - PQStat (rozdział: Ograniczanie obszaru roboczego arkusza). - Selekcja obiektów na podstawie mapy – przykładowo, można wyodrębnić tylko te sklepy, które znajdują się wewnątrz wskazanego na mapie prostokątnego lub eliptycznego obszaru. Obszar ten zaznaczamy korzystając z narzędzi obszaru zaznaczenia a następnie aktywujemy lub dezaktywujemy w oknie
Aktywuj/Dezaktywuj w zaznaczeniudostępnym po wybraniu menuNarzędzia→Aktywuj/Dezaktywuj w zaznaczeniuw oknie Menadżera map.
By aktywować wszystkie obiekty należy wybrać menu Narzędzia →Aktywuj wszystkie w oknie Menadżera map lub menu Edycja →Aktywuj wszystkie w oknie programu PQStat.
2014/08/24 23:54
· admin
Obliczenia geometryczne
Obliczenia geometryczne są to formuły obliczeniowe (patrz Podręcznik Użytkownika - PQStat (rozdział: Formuły)). Formuły dotyczyć mogą danych widocznych w arkuszu lub tych opisujących geometrię mapy.
- Formuły dla danych opisujących geometrię mapy -
funkcje geometryczne/geograficzne
Jako dane do transformacji wybieramy SHP - dane z pliku kształtów.
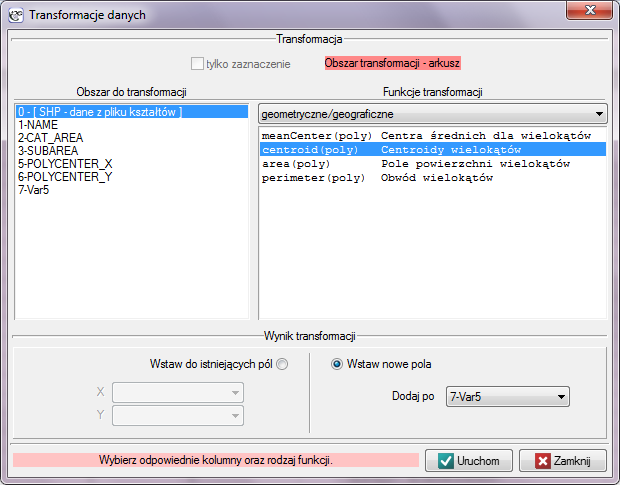
Dostępne formuły:
meanCenter (poly) - zwraca współrzędne centrów dla wielokątów,
centroid (poly) - zwraca współrzędne centroidów dla wielokątów,
area (poly) - zwraca pola powierzchni wielokątów,
perimeter (poly) - zwraca obwody wielokątów.
- Formuły dla danych arkusza -
tworzenie map
Dostępne formuły:
map (points) - zwraca wektorową mapę punktów wraz z przypisanym arkuszem.
2014/08/24 23:53
· admin
Testowanie hipotez
Weryfikacja hipotez statystycznych, to sprawdzanie określonych założeń sformułowanych dla parametrów populacji generalnej na podstawie wyników z próby.
Sformułowanie hipotez, które będą weryfikowane za pomocą testów statystycznych.
Każdy test statystyczny podaje postać ogólną hipotezy zerowej -  (ang. null hypothesis) i alternatywnej -
(ang. null hypothesis) i alternatywnej - 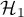 (ang. alternative hypothesis):
(ang. alternative hypothesis):

Przykład:
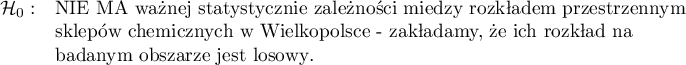
Jeśli nie wiemy, czy rozkład sklepów może być bardziej regularny niż rozkład losowy czy też też odwrotnie - bardziej skupiony niż rozkład losowy, wówczas hipoteza alternatywna powinna być dwustronna, tzn. nie zakładamy kierunku:

Może się zdarzyć (są to bardzo rzadkie przypadki), że mamy pewność, iż znamy kierunek w hipotezie alternatywnej. Wówczas można zastosować jednostronną hipotezę alternatywną.
Weryfikacja hipotez
By sprawdzić, która z hipotez  czy
czy 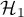 jest bardziej prawdopodobna, dobieramy odpowiedni test statystyczny.
jest bardziej prawdopodobna, dobieramy odpowiedni test statystyczny.
Statystyka testowa wybranego testu wyliczana zgodnie z jej wzorem podlega odpowiedniemu dla niej rozkładowi teoretycznemu.
![LaTeX \psset{xunit=1.25cm,yunit=10cm}
\begin{pspicture}(-5,-0.1)(5,.5)
\psline{->}(-4,0)(4.5,0)
\psTDist[linecolor=green,nue=4]{-4}{4}
\pscustom[fillstyle=solid,fillcolor=cyan!30]{%
\psTDist[linewidth=1pt,nue=4]{-4}{-2.776445}%
\psline(-2.776445,0)(-4,0)}
\pscustom[fillstyle=solid,fillcolor=cyan!30]{%
\psline(2.776445,0)(2.776445,0)%
\psTDist[linewidth=1pt,nue=4]{2.776445}{4}%
\psline(4,0)(2.776445,0)}
\rput(-3.6,0.2){$\alpha/2$}
\psline{->}(-3.6,0.15)(-3.1,0.04)
\rput(3.6,0.2){$\alpha/2$}
\psline{->}(3.6,0.15)(3,0.04)
\rput(1,0.5){$1-\alpha$}
\psline{->}(1,0.46)(0.55,0.35)
\rput(2.5,-0.04){wartość statystyki testowej}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img70973b37fe8a6fdf8dc5c31ade4f7228.png)
Program wylicza wartość statystyki testowej, oraz wartość  dla tej statystyki (czyli część pola pod krzywą, która odpowiada wartości statystyki testowej). Wartość
dla tej statystyki (czyli część pola pod krzywą, która odpowiada wartości statystyki testowej). Wartość  pozwala wybrać spośród hipotezy zerowej i alternatywnej tę bardziej prawdopodobną. Przy czym zawsze zakładamy prawdziwość hipotezy zerowej, a zebrane w danych dowody mają dostarczyć wystarczającej ilości argumentów przeciwko tej hipotezie:
pozwala wybrać spośród hipotezy zerowej i alternatywnej tę bardziej prawdopodobną. Przy czym zawsze zakładamy prawdziwość hipotezy zerowej, a zebrane w danych dowody mają dostarczyć wystarczającej ilości argumentów przeciwko tej hipotezie:

Zwykle wybiera się poziom istotności  , zgadzając się, że w 5% sytuacji odrzucimy hipotezę zerową gdy jest ona prawdziwa. W szczególnych przypadkach można wybrać inny poziom istotności np. 0.01 lub 0.001.
, zgadzając się, że w 5% sytuacji odrzucimy hipotezę zerową gdy jest ona prawdziwa. W szczególnych przypadkach można wybrać inny poziom istotności np. 0.01 lub 0.001.
2014/08/24 23:54
· admin
przestrzenpl/wsteppl.txt · ostatnio zmienione: 2014/08/25 22:44 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

