Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
przestrzenpl:opisowepl
Spis treści
Statystyki opisowe
Statystyki opisowe punktów
By przeprowadzić statystykę opisową powinniśmy dysponować danymi mapy zawierającej obiekty typu: punkt, wielopunkt lub wielokąt. W przypadku analizy wielokątów obliczenia oparte są na centroidach, a przypadku wielopunktów na centrach obiektów.
Granice obszaru, w którym zamknięte są analizowane punkty, w zależności od potrzeb, mogą być zdefiniowane za pomocą: otoczki wypukłej, najmniejszego prostokąta, prostokąta z granic warstwy lub najmniejszego okręgu. Badany obszar może być również zdefiniowany jedynie przez wielkość swojego pola.
Odległość pomiędzy punktami mierzona jest metryką Euklidesową.
Podstawowe statystyki wyznaczane dla analizy punktów:
 - pole powierzchni badanego obszaru,
- pole powierzchni badanego obszaru, - wielkość próby, czyli ilość punktów leżących wewnątrz badanego obszaru,
- wielkość próby, czyli ilość punktów leżących wewnątrz badanego obszaru,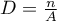 - gęstość,
- gęstość,- statystyki opisowe macierzy odległości pomiędzy punktami:
- średnia arytmetyczna wraz z przedziałem ufności,
- odchylenie standardowe,
- mediana,
- kwartyle,
- minimum i maksimum.
Analiza zwraca również wykres dotyczący macierzy odległości oraz warstwy, które mogą być wyrysowane na płaszczyźnie mapy. Warstwy dotyczą miar centrograficznych: miary tendencji centralnej i rozproszenia:
- Centrum rozkładu punktów: średnia wsółrzędnych osi
 i osi
i osi  (
(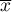 ,
, 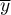 ),
), - Obszar odchyleń standardowych zbudowany wokół centrum, zdefiniowany poprzez:
- Okrąg
Promień okręgu to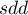 - standardowa odległość od centrum (ang. standard distance deviation) wyrażona wzorem:
- standardowa odległość od centrum (ang. standard distance deviation) wyrażona wzorem:
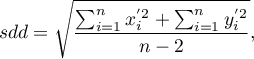
gdzie:
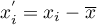 ,
,
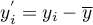 .
.
- Elipsa
Kąt nachylenia osi elipsy (Y) wobec układu współrzędnych (osi OY) wyrażony jest wzorem:
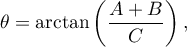
gdzie:
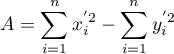 ,
,
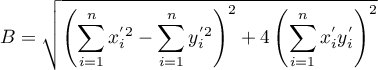 ,
,
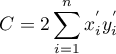 .
.
Długości półosi elipsy:
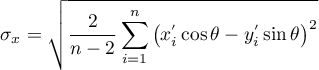
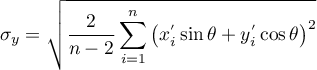
- Prostokąt
Długości boków prostokąta to: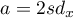 ,
, 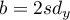 , gdzie
, gdzie 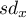 i
i 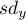 to odchylenia standardowe dla współrzędnych osi
to odchylenia standardowe dla współrzędnych osi  i osi
i osi 
Gdy dla poszczególnych obiektów zostaną zdefiniowane wagi, wówczas wyliczone będzie ważone centrum rozkładu punktów i ważony okrąg przedstawiający obszar odchyleń standardowych
- Ważone centrum rozkładu punktów: ważona średnia współrzędnych osi
 i osi
i osi  :
:
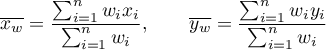
gdzie:
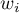 - wagi określające wielkość cechy w
- wagi określające wielkość cechy w  -tym obiekcie.
-tym obiekcie.
- Ważony okrąg
Promień okręgu to - ważona standardowa odległość od centrum wyrażona wzorem:
- ważona standardowa odległość od centrum wyrażona wzorem:
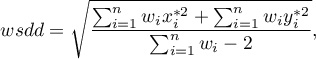
gdzie:
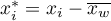 ,
,
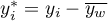 .
.
Uwaga!
We wzorach dotyczących długości promienia okręgu i półosi elipsy, mianownik pomniejszono o wartość 2 - Buliung (2008)1), Smith (2007)2).
Okno z ustawieniami opcji statystyk opisowych wywołujemy poprzez menu Analiza przestrzenna → Przestrzenne statystyki opisowe.
Przykład (katalog: snow, pliki SHP: deaths, pumps, streets)
Dane, których dotyczyć będzie analiza są prawdopodobnie najbardziej znanym, klasycznym przykładem zastosowania kartografii w epidemiologii. Obrazują epidemię cholery w Londynie w roku 1854. Mapę przedstawiającą zakres epidemii sporządził lekarz, odkrywca przyczyny epidemii, uznany za jednego z twórców epidemiologii - John Snow. Współrzędne punktów, które posłużyły do wyrysowania map, pochodzą z oryginalnej mapy stworzonej przez Johna Snowa, która została zdigitalizowana przez Rusty Dodson z US National Center for Geographic Information Analysis (http://ncgia.ucsb.edu/Publications/Software/cholera/) a następnie przedstawiona w metrach.
- Mapa
deathszawiera informacje o lokalizacji 578 punktów (śmierci z powodu cholery) w Soho - jednej z dzielnic Londynu. - Mapa
pumpszawiera informacje o lokalizacji 13 punktów (pomp wodnych) w Soho. - Mapa
streetszawiera informacje o położeniu linii (ulic) w Soho.
Po zaimportowaniu powyższych plików kształtów SHP, możemy każdy z nich obejrzeć i edytować w Menadżerze map.
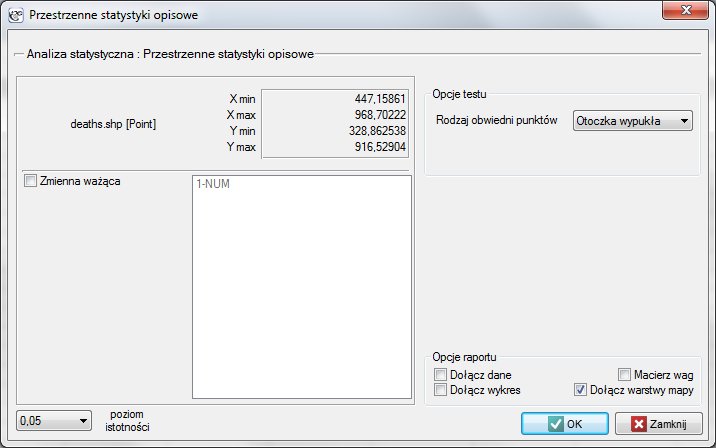
By przeprowadzić analizę zaznaczamy mapę deaths i wykonujemy Przestrzenne statystyki opisowe. Ponieważ jako dane do analizy posłużą nam współrzędne mapy, w oknie statystyk opisowych zaznaczamy opcję Pobierz współrzędne punktów z mapy, jako rodzaj obwiedni obiektów wybieramy otoczkę wypukłą.
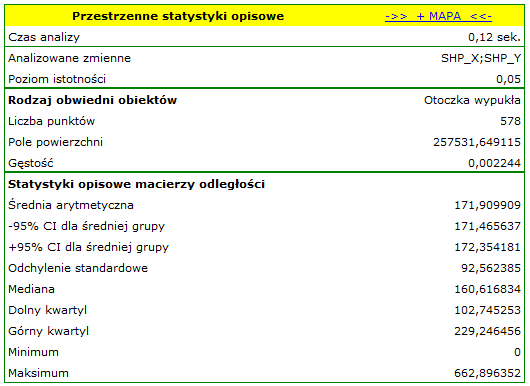
Pole powierzchni, w którym znajdują się punkty (określone przez otoczkę wypukłą) wynosi 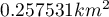 . Możemy je wyrysować na mapie uruchamiając przycisk
. Możemy je wyrysować na mapie uruchamiając przycisk  i wybierając warstwę obwiedni obiektów.
i wybierając warstwę obwiedni obiektów.
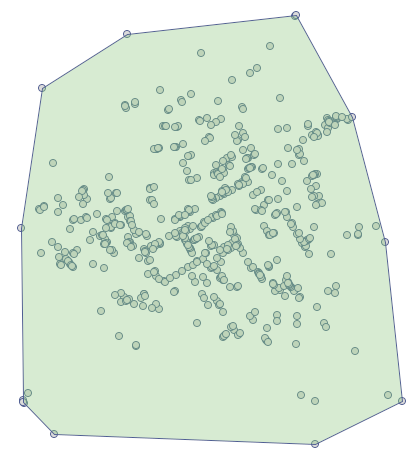
Na 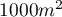 przypada ponad 2 punkty (gęstość=
przypada ponad 2 punkty (gęstość=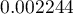 punktów na
punktów na 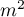 ).
).
Analiza macierzy odległości punktów pozwala na dokładniejszą ocenę ich gęstości. Niektóre punkty znajdują się w tym samym miejscu, ponieważ najmniejsza odległość to 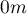 . Są też punkty znacznie bardziej oddalone od siebie - największa odległość to
. Są też punkty znacznie bardziej oddalone od siebie - największa odległość to 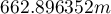 . Znajdujemy tu również informację o przeciętnej odległości i o ich odchyleniu standardowym.
. Znajdujemy tu również informację o przeciętnej odległości i o ich odchyleniu standardowym.
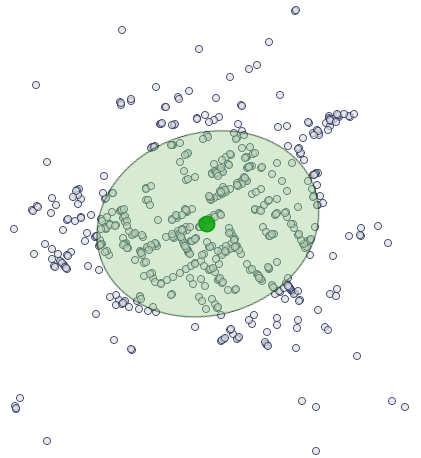
Najbardziej interesującą informację w przypadku analizy mapy deaths daje zlokalizowane Centrum rozkładu punktów (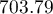 ,
,  ) wraz z obszarem odchyleń standardowych, które opisują stopień koncentracji oraz kierunek dyspersji (okrąg, elipsa, prostokąt).
) wraz z obszarem odchyleń standardowych, które opisują stopień koncentracji oraz kierunek dyspersji (okrąg, elipsa, prostokąt).

Elipsę odchyleń standardowych oraz Centrum wyrysujemy ponownie przechodząc do menadżera map (na liście warstw odznaczamy obwiednię obiektów).
Snow przeprowadził rozmowy z mieszkańcami okolicy i zaczął podejrzewać, że źródłem epidemii może być woda. Połączenie wszystkich trzech map pozwala na zidentyfikowanie pompy wodnej, z której woda okazała się być przyczyną epidemii. By to zrobić w Menadżerze map wyświetlamy najpierw mapę streets a następnie poprzez przycisk  nanosimy na nią mapę
nanosimy na nią mapę deaths i pumps.
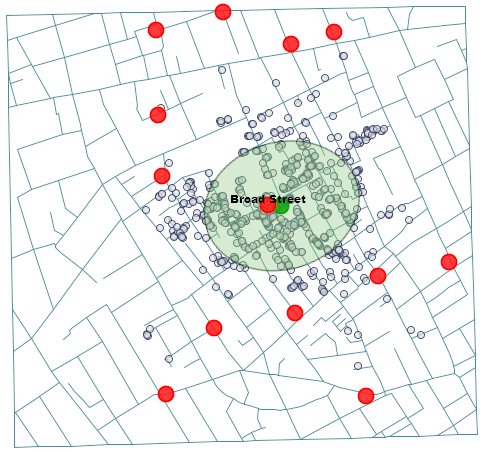
Źródłem epidemii okazuje się być pompa wodna przy ulicy Broad Street (możemy wyświetlić jej etykietę w menadżerze map). Jest to jedyna pompa, która znalazła się w zaznaczonym eliptycznym obszarze, a jej położenie ( ,
, 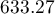 ) i położenie środka elipsy (
) i położenie środka elipsy (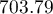 ,
, 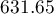 ), czyli miejsca wokół którego skoncentrowane są zgony, jest bardzo bliskie.
), czyli miejsca wokół którego skoncentrowane są zgony, jest bardzo bliskie.
2014/08/25 00:36
· admin
1)
Buliung R.N., Remmel T.K. (2008), Open source, spatial analysis, and activity-travel behaviour research: capabilities of the aspace package. Journal of Geographical Systems 10, 191-216
2)
De Smith M.J., Goodchild M.F., Longley P.A. (2007) , Geospatial Analysis, A Comprehensive Guide to Principles, Techniques and Software Tools (2nd ed). Matador
przestrzenpl/opisowepl.txt · ostatnio zmienione: 2014/08/25 01:02 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


