Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:norm
Spis treści
Testy normalności rozkładu
Testy normalności jednowymiarowej
W badaniu normalności rozkładu zastosowanie mogą mieć różne testy, z których każdy zwraca uwagę na nieco inne aspekty rozkładu Gaussa. Nie można wskazać testu dobrego dla każdego możliwego zestawu danych.
Podstawowy warunek stosowania testów normalności rozkładu:
- pomiar na skali interwałowej.
Hipotezy testów normalności rozkładu:
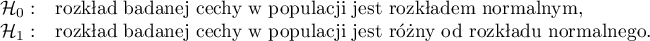
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
Uwaga!!! Badanie normalności rozkładu można przeprowadzać dla zmiennych lub dla różnic wyznaczonych na podstawie dwóch zmiennych.
Test Kołmogorova-Smirnova (ang. Kolmogorov-Smirnov test for normality)
Test zaproponowany przez Kolmogorova (1933)1) jest testem stosunkowo konserwatwnym (trudniej przy jego użyciu udowodnić brak normalności rozkładu). Opiera swoje działanie na wyznaczeniu odległości pomiędzy dystrybuantą empiryczną a teoretyczną rozkładu normalnego. Zaleca się jego stosowanie dla licznych prób, jednak powinien być stosowany w sytuacji, gdy znana jest wartość średnia (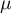 ) i odchylenie standardowe (
) i odchylenie standardowe (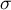 ) dla populacji, z której pochodzi próba. Wówczas możemy sprawdzić, czy rozkład zgodny jest z rozkładem zdefiniowanym przez podaną średnią i odchylenie standardowe.
) dla populacji, z której pochodzi próba. Wówczas możemy sprawdzić, czy rozkład zgodny jest z rozkładem zdefiniowanym przez podaną średnią i odchylenie standardowe.
W oparciu o dane z próby zebrane w skumulowany rozkład częstości oraz o odpowiednie wartości pola pod teoretyczną krzywą rozkładu normalnego wyznaczamy wartość statystyki testowej 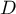 :
:
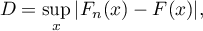
gdzie:
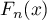 - empiryczna dystrybuanta rozkładu normalnego wyliczana w poszczególnych punktach rozkładu, dla
- empiryczna dystrybuanta rozkładu normalnego wyliczana w poszczególnych punktach rozkładu, dla  -elementowej próby ,
-elementowej próby ,
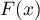 - teoretyczna dystrybuanta rozkładu normalnego.
- teoretyczna dystrybuanta rozkładu normalnego.
Statystyka testu podlega rozkładowi Kołmogorova-Smirnova.
Test Lillieforsa (ang. Lilliefors test for normality)
Test zaproponowany przez Lillieforsa (19672), 19693), 19734)). Jest on poprawką testu Kołmogorova-Smirnova, gdy nie znana jest wartość średnia (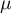 ) i odchylenie standardowe (
) i odchylenie standardowe (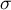 ) dla populacji, z której pochodzi próba. Uznawany jest za nieco mniej konserwatywny od testu Kołmogorova-Smirnova.
) dla populacji, z której pochodzi próba. Uznawany jest za nieco mniej konserwatywny od testu Kołmogorova-Smirnova.
Statystyka testowa 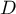 wyznaczana jest na podstawie tej samej formuły, z której korzysta test Kołmogorova-Smirnova, ale podlega rozkładowi Lillieforsa.
wyznaczana jest na podstawie tej samej formuły, z której korzysta test Kołmogorova-Smirnova, ale podlega rozkładowi Lillieforsa.
Test Shapiro-Wilka (ang. Shapiro-Wilk test for normality)
Zaproponowany przez Shapiro oraz Wilka (1965)5) dla mało licznych grup, a następnie zaadoptowany dla grup liczniejszych (do 5000 obiektów) przez Roystona (1992)6)7). Test ten charakteryzuje stosunkowo wysoka moc, co ułatwia dowodzenie braku normalności rozkładu.
Ideę działania testu przedstawia wykres Q-Q plot.
Statystyka testowa Shapiro-Wilka ma postać:
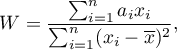
gdzie:
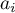 - współczynniki wyznaczane w oparciu o wartości oczekiwane dla statystyk uporządkowanych (ordered statistics), przypisanych wag oraz macierzy kowariancji,
- współczynniki wyznaczane w oparciu o wartości oczekiwane dla statystyk uporządkowanych (ordered statistics), przypisanych wag oraz macierzy kowariancji,
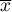 - wartość średnia danych z próby.
- wartość średnia danych z próby.
Statystykę tę przekształca się do statystyki o rozkładzie normalnym:
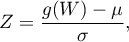
gdzie:
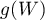 ,
, 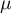 i
i 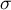 - zależą od wielkości próby:
- zależą od wielkości próby:
- dla prób małych o licznościach 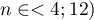 :
:
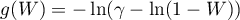 ,
,
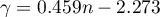 ,
,
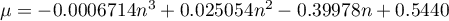 ,
,
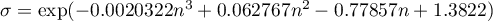 ;
;
- dla prób dużych o licznościach 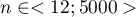 :
:
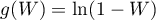 ,
,
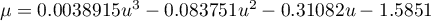 ,
,
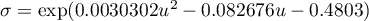 ,
,
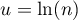 .
.
Test D'Agostino-Pearsona (ang. D'Agostino-Pearson test for normality)
Różne typy analiz statystycznych zakładające normalność są w różnym stopniu wrażliwe na różne rodzaje odejścia od tego założenia. Przyjmuje się, że testy odnoszące się w swoich hipotezach do średnich są bardziej wrażliwe na skośność, a testy porównujące wariancje w większym stopniu zależą od kurtozy.
Rozkład normalny charakteryzować powinna zerowa skośność i zerowa kurtoza g2 (lub b2 bliska wartości trzy). W przypadku braku normalności rozkładu, stwierdzonej przez test D'Agostino (1973)8), można sprawdzić czy jest to efektem wysokiej skośności czy kurtozy poprzez test skośności i test kurtozy.
Podobnie jak test Shapiro-Wilka, test D'Agostino charakteryzuje się większą mocą niż test Kołmogorova-Smirnova i test Lillieforsa (D'Agostino 19909)).
Statystyka testowa ma postać:
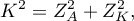
gdzie:
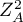 - statystyka testowa testu skośności,
- statystyka testowa testu skośności,
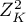 - statystyka testowa testu kurtozy.
- statystyka testowa testu kurtozy.
Statystyka ta ma asymptotycznie rozkład chi-kwadrat z dwoma stopniami swobody.
- Test skośności D'Agostino
Hipotezy:
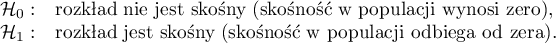
Statystyka testowa ma postać:
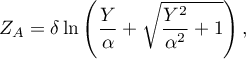
gdzie:
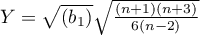 ,
,
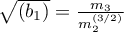 ,
,
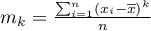 ,
,
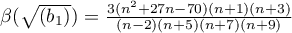 ,
,
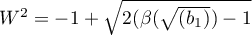 ,
,
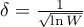 ,
,
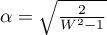 .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
- Test kurtozy D'Agostino
Hipotezy:
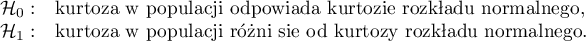
Statystyka testowa ma postać:
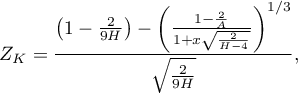
gdzie:
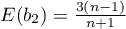 ,
,
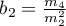 ,
,
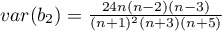 ,
,
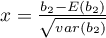 ,
,
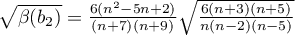 ,
,
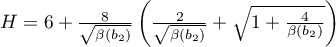 .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wykres Kwantyl-Kwantyl (ang. Q-Q plot, Quantile-Quantile plot)
Wykres typu Kwantyl-Kwantyl wykorzystywany jest do przedstawienia zgodności dwóch rozkładów. W przypadku badania zgodności z rozkładem normalny, sprawdza zgodność rozkładu danych (rozkładu empirycznego) z rozkładem teoretycznym Gaussa. Na jego podstawie można wizualnie sprawdzić jak dobrze krzywa rozkładu normalnego jest dopasowana do danych. Jeśli kwantyle rozkładu teoretycznego i rozkładu empirycznego są zgodne, wówczas punkty rozkładają się wzdłuż linii  . Oś pozioma przedstawia kwantyle rozkładu normalnego, oś pionowa kwantyle rozkładu danych.
. Oś pozioma przedstawia kwantyle rozkładu normalnego, oś pionowa kwantyle rozkładu danych.
Możliwe są bardzo różne odstępstwa od rozkładu normalnego - interpretację kilku najczęściej występujących opisuje schemat:
- dane rozłożone na linii, lecz kilka punktów mocno odbiega od linii
- występują wartości odstające w danych
- punkty po lewej stronie wykresu znajdują się powyżej linii, a po prawej poniżej linii
- rozkład charakteryzuje większa obecność wartości odległych od średniej niż jest w rozkładzie normalnym (ujemna kurtoza)
- punkty po lewej stronie wykresu znajdują się poniżej linii, a po prawej powyżej linii
- rozkład charakteryzuje mniejsza obecność wartości odległych od średniej niż jest w rozkładzie normalnym (dodatnia kurtoza)
- punkty po lewej i po prawej stronie wykresu znajdują się powyżej linii
- rozkład prawostronnie skośny (dodatnia skośność);
- punkty po lewej i po prawej stronie wykresu znajdują się poniżej linii
- rozkład lewostronnie skośny (ujemna skośność).
Okno z ustawieniami opcji testów normalności wywołujemy poprzez menu Statystyka→Testy normalności→Normalność jednowymiarowa lub poprzez ''Kreator''.
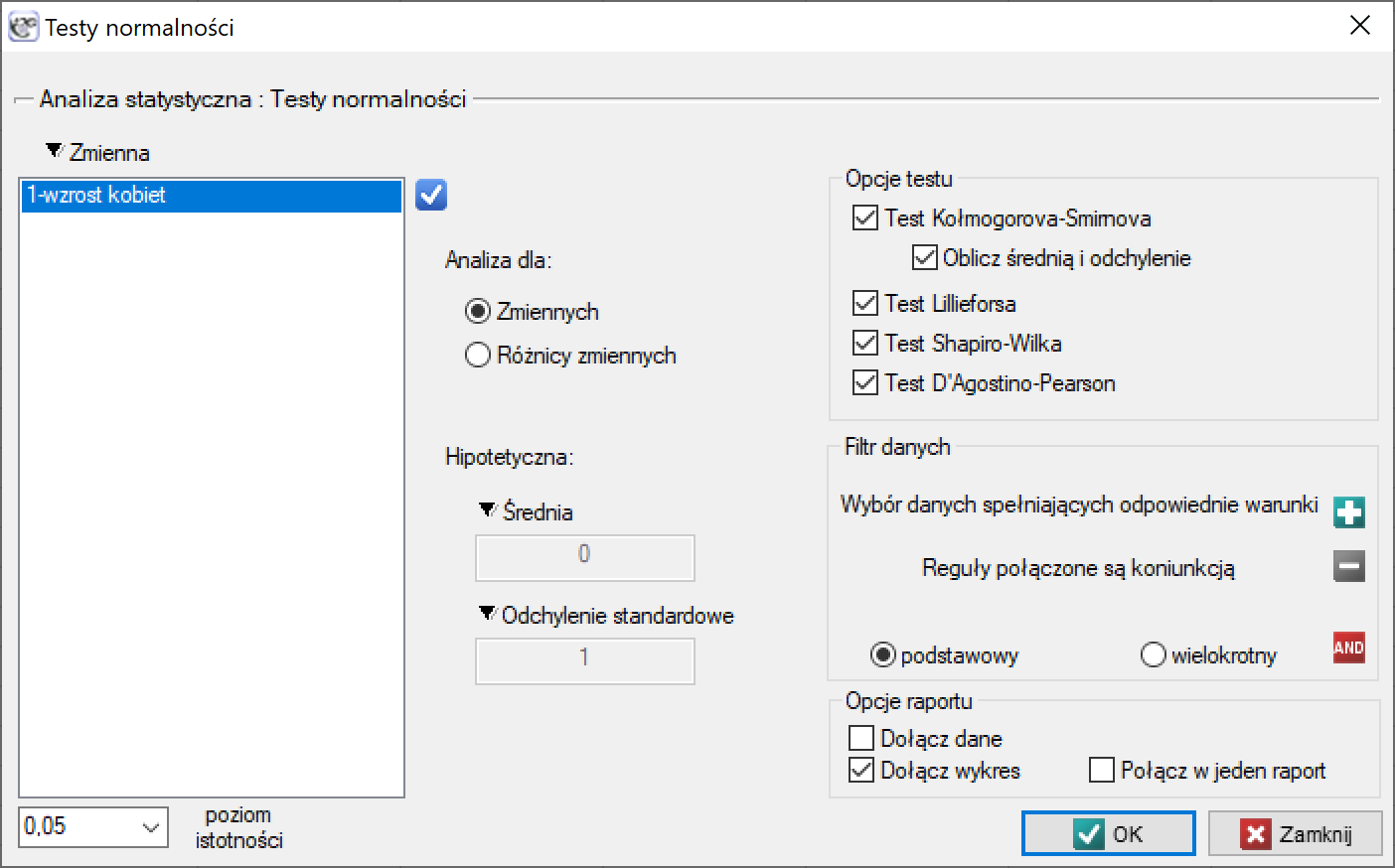
Przykład (plik Gauss.pqs)
Wzrost kobiet
Załóżmy, że wzrost kobiet jest taką cechą, dla której wartość przeciętna wynosi 168cm. Większość kobiet spotykanych na co dzień jest wzrostu, który nie odbiega znacznie od tej przeciętnej. Oczywiście zdarzają się kobiety zupełnie niskie a także bardzo wysokie, ale stosunkowo rzadko. Skoro wartości bardzo niskie i bardzo wysokie występują rzadko, a wartości przeciętne często, możemy się spodziewać, że rozkład wzrostu jest rozkładem normalnym. By się o tym przekonać zmierzono 300 losowo wybranych kobiet.
Hipotezy:

Ponieważ nie znamy średniej ani odchylenia standardowego dla wzrostu kobiet, a jedynie mamy przypuszczenia co do tych wielkości, będą one wyznaczane z próby.
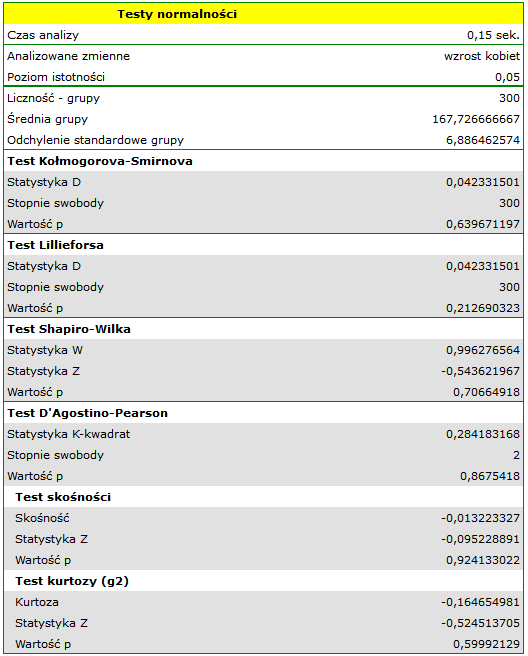
Wszystkie wyznaczone testy wskazują na brak odstępstwa od rozkładu normalnego, ponieważ ich wartości  znajdują się powyżej standardowego poziomu istotności
znajdują się powyżej standardowego poziomu istotności  . Również test badający skośność i kurtozę nie wykazuje odstępstw.
. Również test badający skośność i kurtozę nie wykazuje odstępstw.
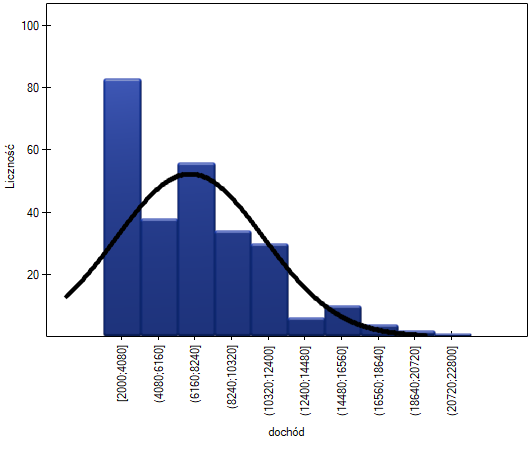
Na wykresie kolumnowym przedstawiliśmy rozkład wzrostu w postaci 10 kolumn. Najliczniejszą grupę stanowią kobiety o wzroście od 167 cm do 171 cm, najmniej liczne są natomiast kobiety niższe niż 150 cm lub wyższe niż 184 cm. Dzwonowa krzywa rozkładu normalnego wydaje się dobrze opisywać ten rozkład.
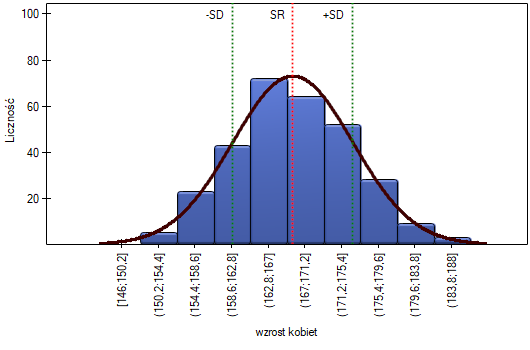
Na wykresie kwantyl-kwantyl punkty leżą prawie idealnie na linii, co również świadczy o bardzo dobrym dopasowaniu rozkładu normalnego.
Rozkład normalny może zatem zostać uznany, za rozkład jakim charakteryzuje się wzrost kobiet w badanej populacji.
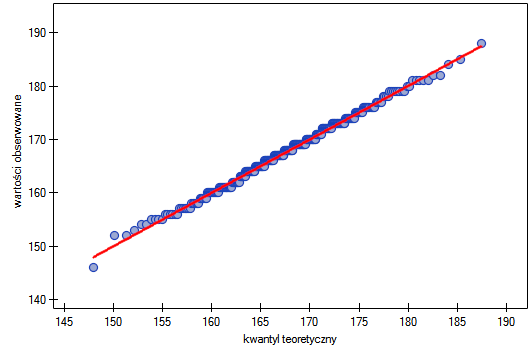
Dochód
Załóżmy, że badamy dochód osób w pewnym kraju. Oczekujemy, że dochody większości osób będą przeciętne, jednak nie będzie osób zarabiających zupełnie mało (poniżej minimalnej pensji narzuconej przez władze), ale będą osoby zarabiające bardzo dużo (prezesi firm) których jest stosunkowo niewielu. By sprawdzić czy dochód osób w badanym kraju ma rozkład normalny zebrano informację o dochodach 264 losowo wybranych osób.
Hipotezy:

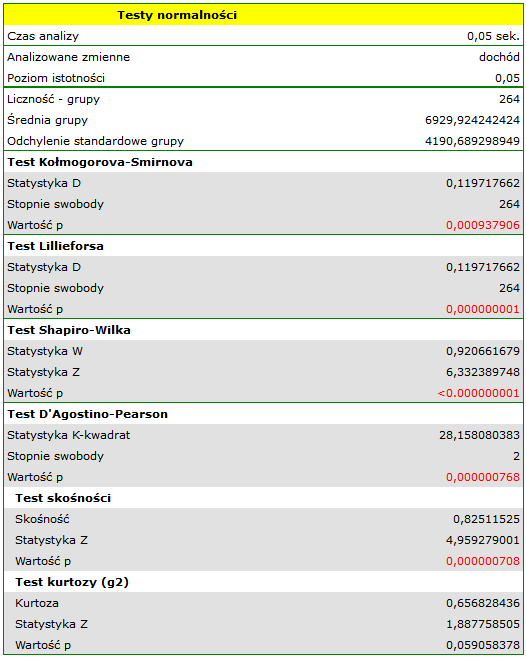
Rozkład nie jest rozkładem normalnym, o czym świadczą wszystkie wyniki testów badających normalność rozkładu ( ). Dodatnia i istotna statystycznie (
). Dodatnia i istotna statystycznie ( ) wartość skośności świadczy o zbyt długim prawym ogonie funkcji. Rozkład funkcji jest również bardziej smukły od rozkładu normalnego, ale nie jest to istotna statystycznie różnica (test kurtozy).
) wartość skośności świadczy o zbyt długim prawym ogonie funkcji. Rozkład funkcji jest również bardziej smukły od rozkładu normalnego, ale nie jest to istotna statystycznie różnica (test kurtozy).
Na wykresie kwartyl-kwartyl odstępstwo od rozkładu normalnego jest obrazowane poprzez skośność prawostronną, czyli położenie znacznie powyżej linii początkowych i końcowych punktów wykresu.
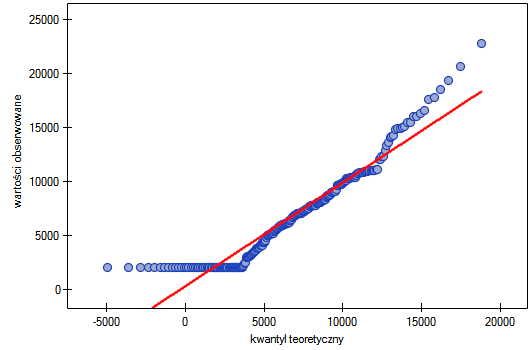
W rezultacie zebrane dane nie świadczą o zgodności rozkładu dochodów z rozkładem normalnym.
aaa
2019/12/17 17:16
· admin
Testy normalności wielowymiarowej
Wiele metod analizy wielowymiarowej, w tym MANOVA, testy Hotellinga czy też modele regresji opierają się na założeniu normalności wielowymiarowej. Jeśli zbiór zmiennych charakteryzuje wielowymiarowy rozkład normalny, to można założyć, że każda zmienna posiada rozkład normalny. Jednak gdy wszystkie pojedyncze zmienne charakteryzowane są rozkładem normalnym, ich zestaw nie musi mieć wielowymiarowego rozkładu normalnego. Dlatego testowanie jednowymiarowej normalności każdej zmiennej może być przydatne, ale nie można założyć, że jest wystarczające.
Różne typy analiz statystycznych zakładające normalność są w różnym stopniu wrażliwe na różne rodzaje odejścia od tego założenia. Przyjmuje się, że testy odnoszące się w swoich hipotezach do średnich są bardziej wrażliwe na skośność, a testy porównujące kowariancje w większym stopniu zależą od kurtozy.
Okno z ustawieniami opcji testu wielowymiarowej normalności rozkładu wywołujemy poprzez menu Statystyka→Testy normalności→Normalność wielowymiarowa.
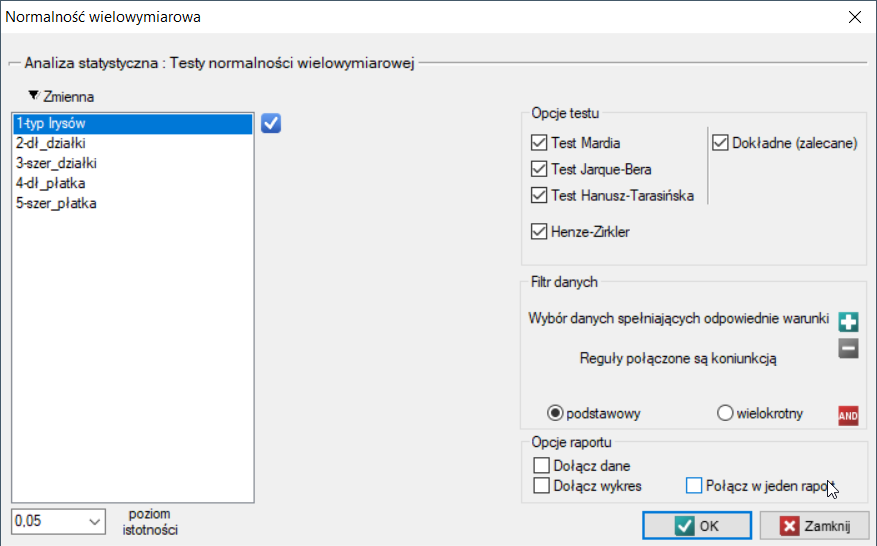
Test Mardia dla wielowymiarowej normalności rozkładu (ang. Mardia's test for multivariate normality)
Test zaproponowany przez Mardia w roku 1970 10) i zmodyfikowany w roku 1974 11) bada normalność rozkładu analizując oddzielnie rozmiar wielowymiarowej skośności i wielowymiarowej kurtozy. Jarque i Bera 12) zaproponowali złączenie tych dwóch miar Mardia w jeden test. Podobny sposób łączenia w jeden test informacji o skośności i kurtozie oferuje metoda Hanusz i Tarasińskiej 13).
Mardia zdefiniował wielowymiarową skośność i kurtozę następująco:
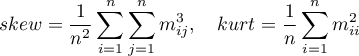 gdzie
gdzie
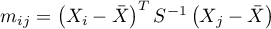 ,
,
 ,
,
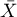 -średnia,
-średnia, 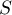 - macierz kowariancji.
- macierz kowariancji.
Dla danych pochodzących z próby, a nie z populacji wzory na skośność i kurtozę są mnożone odpowiednio: skośność przez 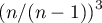 i kurtoza przez
i kurtoza przez 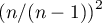 .
.
Hipotezy:
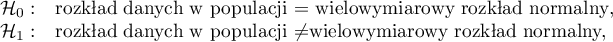
- Mardia test skośności:
Gdy próba pochodzi z populacji o wielowymiarowym rozkładzie normalnym (hipoteza zerowa), to statystyka testowa ma postać (Mardia, 1970):
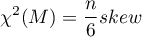
lub z poprawką dokładnych momentów dla grup o mniejszych licznościach (<20) (Mardia, 1974):
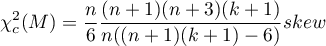
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 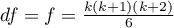 stopniami swobody.
stopniami swobody.
- Mardia test kurtozy:
Gdy próba pochodzi z populacji o wielowymiarowym rozkładzie normalnym (hipoteza zerowa), to statystyka testowa ma postać (Mardia, 1974):
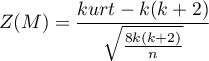
lub z poprawką (Mardia, 1974):
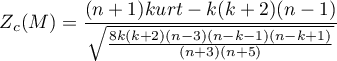
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
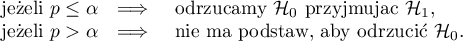
Test Jarque-Bera dla wielowymiarowej normalności rozkładu (ang. Jarque-Bera test for multivariate normality)
Test Jarque i Bera (1987) 14) bazuje na statystyce skośności i kurtozy testu Mardia. Statystyka testowa ma postać:
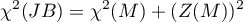
lub z poprawką (Mardia, 1974):
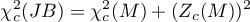
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 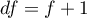 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
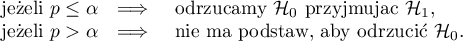
Test Hanusz-Tarasińska dla wielowymiarowej normalności rozkładu (ang. Hanusz-Tarasinska test for multivariate normality)
Test Zofii Hanusz i Joanny Tarasińskiej (2014) 15) bazuje na statystyce skośności i kurtozy testu Mardia. Statystyka testowa ma postać:
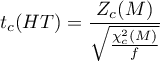
Statystyka testowa ma rozkład t-Studenta z 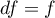 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
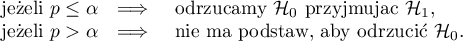
Test Henze-Zirklera dla wielowymiarowej normalności rozkładu (ang. Henze-Zirkler test for multivariate normality)
Henze i Zirklera (1990) 16) zaproponowali test badający wielowymiarową normalność rozkładu rozszerzając pracę Baringhausa i Henzego nad empiryczną funkcją charakterystyczną 17). W literaturze jest to test uznawany za jeden z najsilniejszych testów poświęconych wielowymiarowemu rozkładowi normalnemu (Thode 2002) 18). Statystyka testowa ma postać:
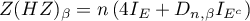
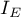 oraz
oraz 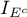 to funkcje indykatorowe zależne od osobliwości macierzy kowariancji,
to funkcje indykatorowe zależne od osobliwości macierzy kowariancji,
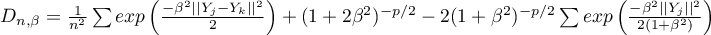
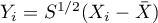
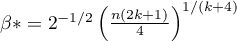 - optymalna wartość parametru
- optymalna wartość parametru 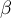
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny oparty na średniej i wariancji opisanej przez Henze i Zirklera i odczytywany jednostronnie.
ma asymptotycznie (dla dużych liczności) rozkład normalny oparty na średniej i wariancji opisanej przez Henze i Zirklera i odczytywany jednostronnie.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
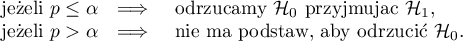
Przykład (plik Irysy.pqs)
Badamy normalność rozkładu dla klasycznego zestawu danych R.A. Fishera 1936 19). Plik znajduje się w pomocy dołączonej do programu i zawiera pomiary długości i szerokości płatków i działek kielicha dla 3 odmian kwiatu irysa. Analiza zostanie przeprowadzona oddzielnie dla każdej odmiany.
W oknie analizy zaznaczamy wszystkie testy oraz wykres, a w celu powtórzenia analizy dla każdej odmiany irysa ustawiamy filtr wielokrotny. Wszystkie wyniki zwrócimy do tego samego arkusza, dlatego zaznaczamy opcję Połącz w jeden raport.
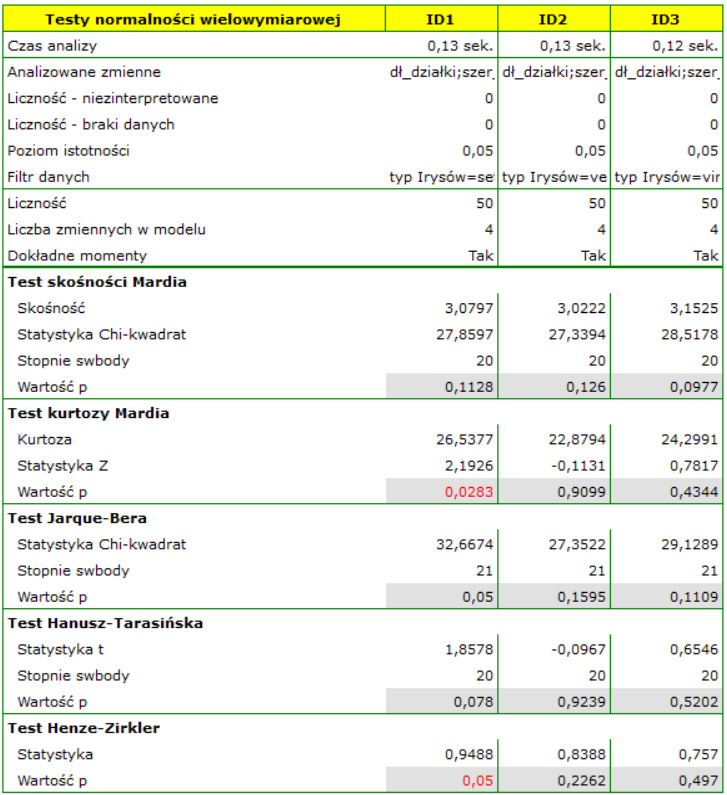
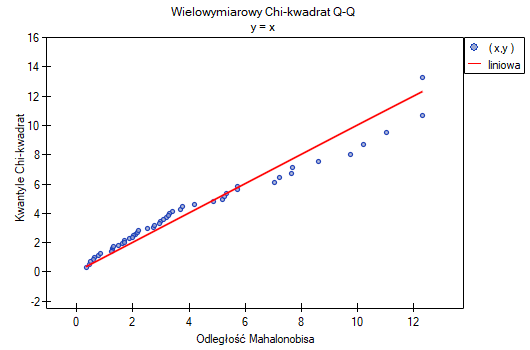
Wszystkie tety potwierdzają normalność rozkładu dla odmiany versicolor i virginica. W przypadku odmiany setosa wyniki testów są na pograniczu istotności statystycznej, przy czym test Mardia dla Kurtozy i test Henze-Zirkler wskazują na odstępstwa od wielowymiarowego rozkładu normalnego. Możemy obserwować takie odstępstwa również na pierwszym wykresie, gdzie wraz narastaniem odległości Mahalanobisa punkty znajdują się coraz dalej od prostej.
2019/12/17 17:18
· admin
1)
Kolmogorov A.N. (1933), Sulla deterrninazione empirica di una legge di distribuzione. Giornde1l'Inst. Ital. degli. Art., 4, 89-91
2)
Lilliefors H.W. (1967), On the Kolmogorov-Smimov test for normality with mean and variance unknown. Journal of the American Statistical Association, 62,399-402
3)
Lilliefors H.W. (1969), On the Kolmogorov-Smimov test for the exponential distribution with mean unknown. Journal of the American Statistical Association, 64,387-389
4)
Lilliefors H.W. (1973), The Kolmogorov-Smimov and other distance tests for the gamma distribution and for the extreme-value distribution when parameters must be estimated. Department of Statistics, George Washington University, unpublished manuscript
5)
Shapiro S.S. and Wilk M.B. (1965), An analysis of variance test for normality (complete samples). Biometrika 52 (3–4): 591–611
6)
Royston P. (1992), Approximating the Shapiro–Wilk W-test for non-normality„. Statistics and Computing 2 (3): 117–119
7)
Royston P. (1993b), A toolkit for testing for non-normality in complete and censored samples. Statistician 42: 37–43
8)
D'Agostino R.B. and Pearson E.S. (1973), Tests of departure from normality. Empirical results for the distribution of b2 and sqrt(b1). Biometrika, 60, 613-622
9)
D'Agostino R.B., Belanger A., D'Agostino Jr.R B. (1990), A suggestion for using powerful and informative tests of normality. American Statistician, 44, 3 16-321
10)
Mardia K. V. (1970), Measures of multivariate skewness and kurtosis with applications, Biometrica 57, 519-530
11)
Mardia K. V. (1974), Applications of some measuresof multivariate skewness and kurtosis for testing normality and robustness studies, Sankhay B 36, 115-128
12)
, 14)
Jarque C. M., Bera A. K., (1987)., A test for normality of Observations and Regression Residuals, International Statistical Review 55, 163-172
13)
, 15)
Hanusz Z., Tarasińska J. (2014), On multivariate normality tests using skewness and kurtosis, Colloquium Biometricum 44, 139-148
16)
Henze N., Zirkler B. (1990), A class of invariant consistent tests for multivariate normality. Comm. Statist. Theory Methods. 1990;19:3595–3617
17)
Epps T.W., Pulley L.B. (1983), A test for normality based on the empirical characteristic function. Biometrika. 1983;70:723–726
18)
Thode H. C. (2002), Testing For Normality. CRC Press; 2002. 506 s.
19)
Fisher R.A. (1936), The use of multiple measurements in taxonomic problems. Annals of Eugenics 7 (2): 179–188
statpqpl/norm.txt · ostatnio zmienione: 2019/12/17 20:58 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


