Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown1grpl
Spis treści
Porównanie - 1 grupa
{\ovalnode{A}{\hyperlink{rozklad_normalny}{\begin{tabular}{c}Czy rozkład\\zmiennej jest\\rozkładem\\normalnym?\end{tabular}}}}
\rput[br](2.7,7.2){\rnode{B}{\psframebox{\hyperlink{test_t_student}{\begin{tabular}{c}test\\t-Studenta\\dla jednej\\grupy\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{B}
\rput(2.2,10.4){T}
\rput(4.3,12.5){N}
\rput(7.5,14){\hyperlink{porzadkowa}{Skala porzadkowa}}
\rput[br](8.9,11.2){\rnode{C}{\psframebox{\hyperlink{test_wilcoxon_rangowanych_znakow}{\begin{tabular}{c}test\\rangowanych\\znaków\\Wilcoxona\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{C}
\rput(12.5,14){\hyperlink{nominalna}{Skala nominalna}}
\rput[br](13.8,10.5){\rnode{D}{\psframebox{\begin{tabular}{c}\hyperlink{test_chi_kwadrat_dobroci}{test $\chi^2$}\\\hyperlink{test_chi_kwadrat_dobroci}{(dobroci}\\\hyperlink{test_chi_kwadrat_dobroci}{dopasowania),}\\\hyperlink{test_z_dla_proporcji}{testy dla} \\\hyperlink{test_z_dla_proporcji}{jednej}\\\hyperlink{test_z_dla_proporcji}{proporcji}\\\end{tabular}}}}
\rput(6,10){\hyperlink{testy_normalnosci}{testy normalności}}
\rput(6,9.5){\hyperlink{testy_normalnosci}{rozkładu}}
\psline[linestyle=dotted]{<-}(3.4,11.2)(4,10.2)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img200a9cc754e142b3e929fb5edea53953.png)
Testy parametryczne
Test t-Studenta dla pojedynczej próby
Test t-Studenta dla pojedynczej próby (ang. single-sample t test) służy do weryfikacji hipotezy, że badana próba o średniej 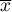 pochodzi z populacji dla której średnia
pochodzi z populacji dla której średnia 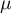 to zadana wartość.
to zadana wartość.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanej cechy.
Hipotezy:
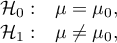
gdzie:
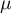 - średnia cechy w populacji reprezentowanej przez próbę,
- średnia cechy w populacji reprezentowanej przez próbę,
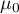 - zadana wartość.
- zadana wartość.
Statystyka testowa ma postać:
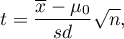
gdzie:
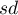 - odchylenie standardowe z próby,
- odchylenie standardowe z próby,
 - liczność próby.
- liczność próby.
Statystyka testowa ma rozkład t-Studenta z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
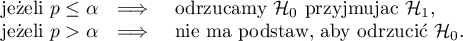
Uwaga!
Gdy próba jest duża i znane jest odchylenie standardowe z populacji wówczas statystykę testową można wyznaczyć z wzoru:
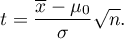 Tak wyznaczona statystyka testowa ma rozkład normalny. Przy
Tak wyznaczona statystyka testowa ma rozkład normalny. Przy 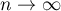 rozkład
rozkład  -Studenta jest zbieżny do rozkładu normalnego
-Studenta jest zbieżny do rozkładu normalnego 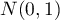 . W praktyce przyjmuje się, że dla
. W praktyce przyjmuje się, że dla  rozkład
rozkład  -Studenta można aproksymować rozkładem normalnym.
-Studenta można aproksymować rozkładem normalnym.
Standaryzowana wielkość efektu
Współczynnik d-Cohena określa jak dużą częścią występującej zmienności jest różnica między średnimi.
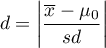
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 1) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu t-Studenta dla pojedynczej próby wywołujemy poprzez menu Statystyka→Testy parametryczne→t-Student lub poprzez ''Kreator''.
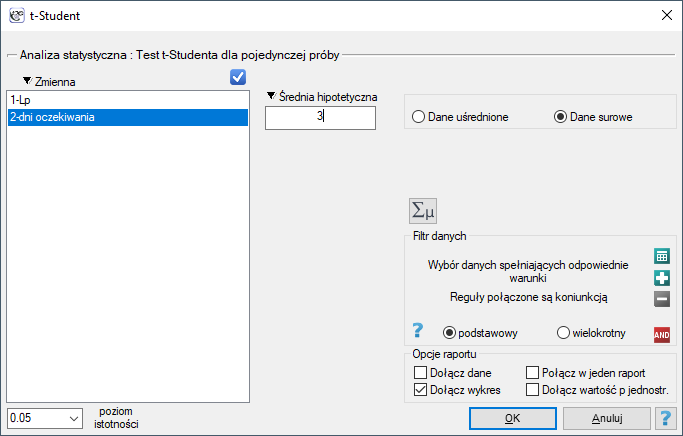
Uwaga!
Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. średniej arytmetycznej, odchyleniu standardowym i liczności próby.
Przykład (plik kurier.pqs)
Chcemy sprawdzić, czy czas oczekiwania na dostarczenie przesyłki przez pewna firmę kurierską to przeciętnie 3 dni 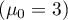 . W tym celu z populacji klientów tej firmy wylosowano próbę liczącą 22 osoby i zapisano informacje o liczbie dni, jakie minęły od dnia nadania przesyłki do jej dostarczenia, były to następujące wielkości: (1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7).}
. W tym celu z populacji klientów tej firmy wylosowano próbę liczącą 22 osoby i zapisano informacje o liczbie dni, jakie minęły od dnia nadania przesyłki do jej dostarczenia, były to następujące wielkości: (1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7).}
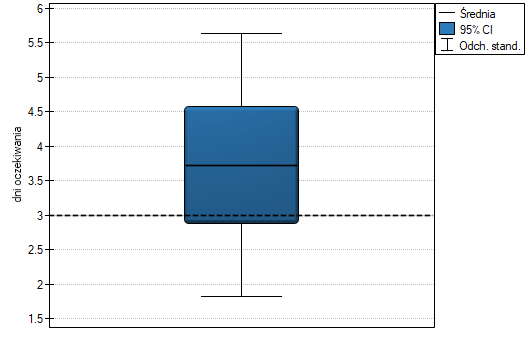
Liczba dni oczekiwania na przesyłkę w badanej populacji spełnia założenie normalności rozkładu.
Hipotezy:


Porównując wartość 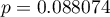 testu
testu  -Studenta z poziomem istotności
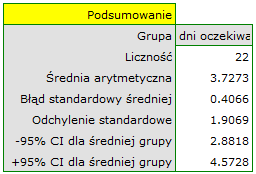
-Studenta z poziomem istotności  stwierdzamy, że nie ma podstaw by odrzucić hipotezę zerową mówiącą, że średnia liczba dni oczekiwania na dostarczenie przesyłki przez analizowaną firmę kurierską wynosi 3. Dla badanej próby średnia to
stwierdzamy, że nie ma podstaw by odrzucić hipotezę zerową mówiącą, że średnia liczba dni oczekiwania na dostarczenie przesyłki przez analizowaną firmę kurierską wynosi 3. Dla badanej próby średnia to 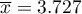 a odchylenie standardowe
a odchylenie standardowe 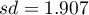 .
.
2014/08/22 20:00
2014/08/22 20:00
Testy nieparametryczne
Test Wilcoxona (rangowanych znaków)
Test Wilcoxona rangowanych znaków (ang. Wilcoxon signed-ranks test) znany również pod nazwą testu Wilcoxona dla pojedynczej próby, Wilcoxon (1945, 1949)2). Test ten służy do weryfikacji hipotezy, że badana próba pochodzi z populacji, dla której mediana (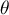 ) to znana wartość.
) to znana wartość.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej.
Hipotezy dotyczą równości sumy rang dodatnich i ujemnych lub są upraszczane do median:
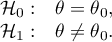
gdzie:
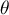 - mediana badanej cechy w populacji reprezentowanej przez badaną próbę,
- mediana badanej cechy w populacji reprezentowanej przez badaną próbę,
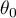 - zadana wartość.
- zadana wartość.
Wyznaczamy wartość statystyki testowej  (
(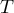 - dla małej liczności próby), a na jej podstawie wartość
- dla małej liczności próby), a na jej podstawie wartość  .
.
Porównujemy wartość  z poziomem istotności
z poziomem istotności  :
:
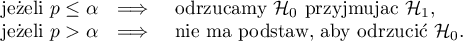
Uwaga!
W zależności od wielkości próby statystyka testowa przyjmuje inną postać:
- dla małej liczności próby
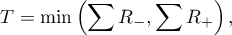
gdzie: 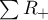 i
i 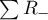 to odpowiednio: suma rang dodatnich i suma rang ujemnych.
to odpowiednio: suma rang dodatnich i suma rang ujemnych.
Statystyka ta podlega rozkładowi Wilcoxona
- dla próby o dużej liczności
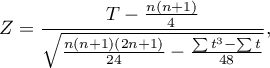
gdzie:  - liczba rangowanych znaków (liczba rang),
- liczba rangowanych znaków (liczba rang),
 - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta powinna być stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
zawiera poprawkę na rangi wiązane. Poprawka ta powinna być stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 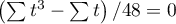 .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Poprawka na ciągłość testu Wilcoxona (Marascuilo and McSweeney (1977)3))
Poprawkę na ciągłość stosujemy by zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu normalnego. Wzór na statystykę testową z poprawką na ciągłość wyraża się wtedy wzorem:
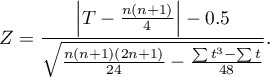
Standaryzowana wielkość efektu
Rozkład statystyki testu Wilcoxona jest aproksymowany przez rozkłady normalny, który można przekształcić na wielkość efektu 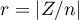 4) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
4) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
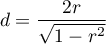
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 5) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu Wilcoxona (rangowanych znaków) wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Wilcoxon (rangowanych znaków) lub poprzez ''Kreator''.
Przykład (plik kurier.pqs) c.d
Hipotezy:

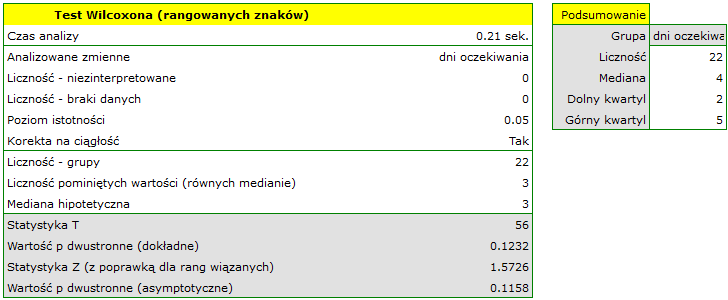
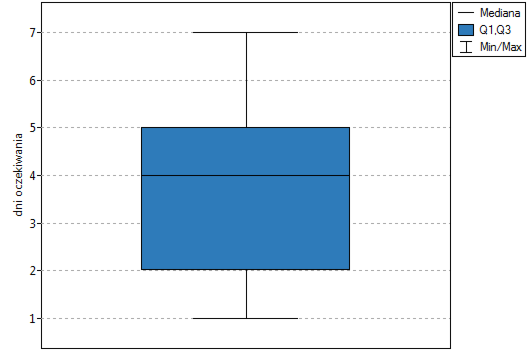
Porównując wartość 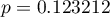 testu Wilcoxona opartego o statystykę
testu Wilcoxona opartego o statystykę  z poziomem istotności
z poziomem istotności  stwierdzamy, że nie mamy podstaw by odrzucić hipotezę zerową mówiącą, że zwykle liczba dni oczekiwania na dostarczenie przesyłki przez analizowaną firmę kurierską wynosi 3. Taką samą decyzję podjęlibyśmy również na podstawie wartości
stwierdzamy, że nie mamy podstaw by odrzucić hipotezę zerową mówiącą, że zwykle liczba dni oczekiwania na dostarczenie przesyłki przez analizowaną firmę kurierską wynosi 3. Taką samą decyzję podjęlibyśmy również na podstawie wartości 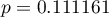 lub
lub 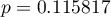 testu Wilcoxona opartego o statystykę
testu Wilcoxona opartego o statystykę  lub
lub  z poprawką na ciągłość.
z poprawką na ciągłość.
2014/08/22 20:00
Test chi-kwadrat zgodności
Test  zgodności (dobroci dopasowania) (ang. Chi-square goodnes-of-fit test) nazywany jest również testem
zgodności (dobroci dopasowania) (ang. Chi-square goodnes-of-fit test) nazywany jest również testem  dla pojedynczej próby, przeznaczony jest do testowania zgodności wartości obserwowanych dla
dla pojedynczej próby, przeznaczony jest do testowania zgodności wartości obserwowanych dla  (
(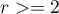 ) kategorii
) kategorii 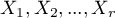 jednej cechy
jednej cechy  z hipotetycznymi wartościami oczekiwanymi dla tej cechy. Wartości wszystkich
z hipotetycznymi wartościami oczekiwanymi dla tej cechy. Wartości wszystkich  pomiarów należy zebrać w postaci tabeli składającej się z
pomiarów należy zebrać w postaci tabeli składającej się z  wierszy (kategorii:
wierszy (kategorii: 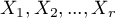 ). Dla każdej kategorii
). Dla każdej kategorii 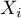 zapisuje się częstość jej występowania
zapisuje się częstość jej występowania 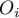 , oraz częstość dla niej oczekiwaną
, oraz częstość dla niej oczekiwaną 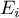 lub prawdopodobieństwo jej wystąpienia
lub prawdopodobieństwo jej wystąpienia 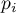 . Częstość oczekiwana jest wyznaczana jako iloczyn
. Częstość oczekiwana jest wyznaczana jako iloczyn 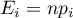 .
.
Utworzona tabela może przyjąć jedną z poniższych postaci:
![LaTeX \begin{tabular}[t]{c@{\hspace{1cm}}c}
\begin{tabular}{c|c c}
Kategorie $X_i$ & $O_i$ & $E_i$ \\\hline
$X_1$ & $O_1$ & $E_i$ \\
$X_2$ & $O_2$ & $E_2$ \\
... & ... & ...\\
$X_r$ & $O_r$ & $E_r$ \\
\end{tabular}
&
\begin{tabular}{c|c c}
Kategorie $X_i$ & $O_i$ & $p_i$ \\\hline
$X_1$ & $O_1$ & $p_1$ \\
$X_2$ & $O_2$ & $p_2$ \\
... & ... & ...\\
$X_r$ & $O_r$ & $p_r$ \\
\end{tabular}
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img53c42b4f4572477f9cbd987271a3d7c9.png)
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
- suma liczności obserwowanych powinna być taka sama jak suma liczności oczekiwanych, a suma wszystkich prawdopodobieństw
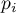 powinna wynosić 1.
powinna wynosić 1.
Hipotezy:
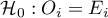 dla wszystkich kategorii,
dla wszystkich kategorii,
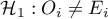 dla przynajmniej jednej kategorii.
dla przynajmniej jednej kategorii.
Statystyka testowa ma postać:
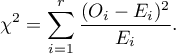 Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru:
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 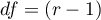 .
.
Wyznaczoną na podstawie wartości statystyki i rozkładu  wartość
wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
Okno z ustawieniami opcji testu Chi-kwadrat zgodności wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat lub poprzez ''Kreator''.
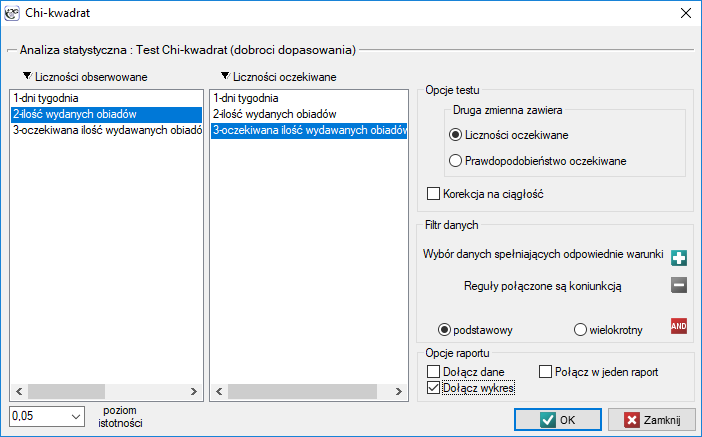
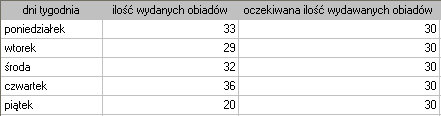
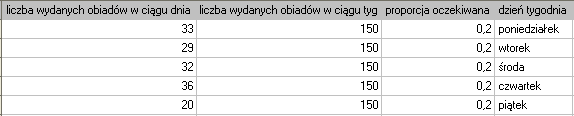
Chcielibyśmy się dowiedzieć, czy liczba wydawanych obiadów w kolejnych dniach tygodnia (od poniedziałku do piątku) w pewnej szkolnej stołówce jest statystycznie taka sama. W tym celu pobrano tygodniową próbę i zapisano dla niej liczbę wydanych obiadów w poszczególnych dniach: poniedziałek - 33, wtorek - 29, środa - 32, czwartek - 36, piątek - 20.}
Łącznie przez cały tydzień (5 dni) wydano 150 obiadów.
Zakładamy, że w każdy dzień prawdopodobieństwo wydania obiadu jest takie samo, czyli wynosi 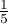 . Oczekiwana liczba wydanych obiadów dla każdego z pięciu dni tygodnia wynosi więc
. Oczekiwana liczba wydanych obiadów dla każdego z pięciu dni tygodnia wynosi więc 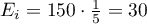 .
.
Postawiono hipotezy:
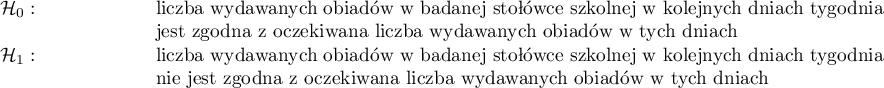
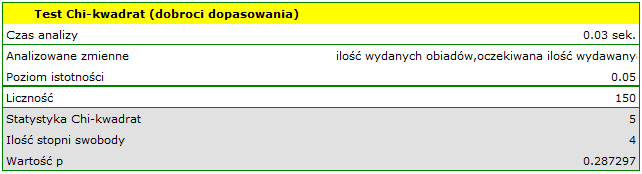
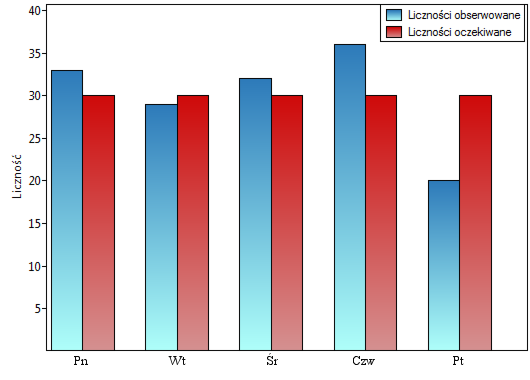
Wartość  z rozkładu
z rozkładu  dla 4 stopni swobody wynosi 0.287297. Zatem na poziomie istotności
dla 4 stopni swobody wynosi 0.287297. Zatem na poziomie istotności  możemy powiedzieć, że nie mamy podstaw, aby odrzucić hipotezę zerową mówiącą o zgodności liczby wydawanych obiadów z oczekiwaną liczbą wydawanych obiadów w poszczególnych dniach.
możemy powiedzieć, że nie mamy podstaw, aby odrzucić hipotezę zerową mówiącą o zgodności liczby wydawanych obiadów z oczekiwaną liczbą wydawanych obiadów w poszczególnych dniach.
Uwaga!
Gdybyśmy chcieli w ramach jednego badania dokonać większej liczby porównań, moglibyśmy zastosować poprawkę Bonferroniego 7) lub inną z poprawek opisanych w dziale Wielokrotne porównania. Ta poprawka jest używana by ograniczyć wielkość popełnionego błędu pierwszego rodzaju, gdy porównujemy wartości obserwowane i oczekiwane pomiędzy wybranymi dniami np:
Pt  Pn,
Pn,
Pt  Wt,
Wt,
Pt  Śr,
Śr,
Pt  Czw,
Czw,
przy założeniu, że porównania wykonujemy niezależnie. Poziom istotności  dla każdego porównania wyznaczamy zgodnie z tą poprawką według wzoru:
dla każdego porównania wyznaczamy zgodnie z tą poprawką według wzoru: 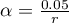 , gdzie
, gdzie  to liczba wykonywanych porównań. Poziom istotności dla pojedynczego porównania zgodnie z poprawką Bonferroniego wynosi dla naszego przykładu
to liczba wykonywanych porównań. Poziom istotności dla pojedynczego porównania zgodnie z poprawką Bonferroniego wynosi dla naszego przykładu 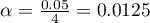 .
.
Należy jednak pamiętać, że redukując  dla każdego porównania zmniejszamy również moc testu.
dla każdego porównania zmniejszamy również moc testu.
2014/08/22 20:00
Testy dla jednej proporcji
Testy dla jednej proporcji stosujemy, gdy mamy do uzyskania dwa możliwe wyniki (jeden z nich to wynik wyróżniony o liczności  ) i wiemy, jak często te wyniki pojawiają się w próbie (znamy proporcję
) i wiemy, jak często te wyniki pojawiają się w próbie (znamy proporcję  ). W zależności od wielkości próby
). W zależności od wielkości próby  mamy do wyboru test
mamy do wyboru test  dla jednej proporcji
dla jednej proporcji  dla dużych prób oraz test dokładny dwumianowy
dla dużych prób oraz test dokładny dwumianowy  dla prób o małej liczności. Testy te służą do weryfikacji hipotezy, że proporcja w populacji z której pochodzi próba to zadana wartość.
dla prób o małej liczności. Testy te służą do weryfikacji hipotezy, że proporcja w populacji z której pochodzi próba to zadana wartość.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę.
Dodatkowy warunek dla testu  dla jednej proporcji:
dla jednej proporcji:
Hipotezy:
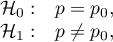
gdzie:

 prawdopodobieństwo (wyróżniona proporcja) w populacji,
prawdopodobieństwo (wyróżniona proporcja) w populacji,
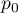
 prawdopodobieństwo oczekiwane (proporcja oczekiwana).
prawdopodobieństwo oczekiwane (proporcja oczekiwana).
Test  dla jednej proporcji
dla jednej proporcji
Test  dla jednej proporcji (ang. Z test for one proportion).
dla jednej proporcji (ang. Z test for one proportion).
Statystyka testowa ma postać:
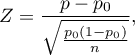 gdzie:
gdzie:
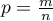 proporcja dla próby z tej populacji,
proporcja dla próby z tej populacji,
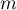 -liczność wartości wyszczególnionych w próbie,
-liczność wartości wyszczególnionych w próbie,
 - liczność próby.
- liczność próby.
Zmodyfikowana o poprawkę na ciągłość statystyka testowa ma postać:
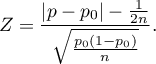
Statystyka  bez korekcji na ciągłość jak i z tą korekcją ma asymptotycznie (dla dużych liczności) rozkład normalny.
bez korekcji na ciągłość jak i z tą korekcją ma asymptotycznie (dla dużych liczności) rozkład normalny.
Test dwumianowy
Test dwumianowy (ang. Binominal test for one proportion) wykorzystuje w sposób bezpośredni rozkład dwumianowy zwany również rozkładem Bernoulliego, który należy do grupy rozkładów dyskretnych (czyli takich, w których badana zmienna przyjmuje skończoną liczbę wartości). Analizowana zmienna może przyjmować 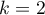 wartości, pierwszą oznaczaną zwykle mianem sukcesu a drugą porażki. Prawdopodobieństwo wystąpienia sukcesu to
wartości, pierwszą oznaczaną zwykle mianem sukcesu a drugą porażki. Prawdopodobieństwo wystąpienia sukcesu to 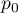 , a porażki
, a porażki 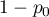 .
.
Prawdopodobieństwo dla konkretnego punktu w tym rozkładzie wyliczane jest ze wzoru:
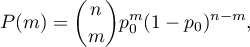 gdzie:
gdzie:
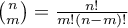 ,
,
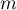 - liczność wartości wyszczególnionych w próbie,
- liczność wartości wyszczególnionych w próbie,
 - liczność próby.
- liczność próby.
Na podstawie sumy odpowiednich prawdopodobieństw 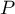 wyznacza się wartość
wyznacza się wartość  jednostronną i dwustronną, przy czym dwustronna wartość
jednostronną i dwustronną, przy czym dwustronna wartość  jest definiowana jako podwojona wartość mniejszego z jednostronnych prawdopodobieństw. Wartość
jest definiowana jako podwojona wartość mniejszego z jednostronnych prawdopodobieństw. Wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
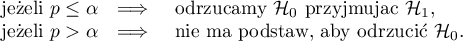
Uwaga!
Dla estymatora z próby jakim jest w tym przypadku wartość proporcji  wyznacza się przedział ufności. Dla prób o dużej liczności można bazować na przedziałach opartych o rozkład normalny - tzw. przedziały Walda. Bardziej uniwersalne są natomiast przedziały zaproponowane przez Wilsona (1927)9) a także Agresti i Coull (1998)10). Przedziały Cloppera i Pearsona (1934)11) są dokładniejsze dla prób o mniejszej liczności.
wyznacza się przedział ufności. Dla prób o dużej liczności można bazować na przedziałach opartych o rozkład normalny - tzw. przedziały Walda. Bardziej uniwersalne są natomiast przedziały zaproponowane przez Wilsona (1927)9) a także Agresti i Coull (1998)10). Przedziały Cloppera i Pearsona (1934)11) są dokładniejsze dla prób o mniejszej liczności.
Porównanie metod budowania przedziałów dla proporcji można znaleźć w pracy Brown L.D i innych (2001)12).
Okno z ustawieniami opcji testu Z dla jednej proporcji wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Z dla proporcji.
Przykład c.d. (plik obiady.pqs)
Załóżmy, że chcielibyśmy sprawdzić, czy w piątek wydawana jest 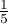 spośród wszystkich obiadów wydawanych w szkolnej stołówce w ciągu tygodnia. Dla pobranej próby
spośród wszystkich obiadów wydawanych w szkolnej stołówce w ciągu tygodnia. Dla pobranej próby  ,
, 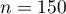 .
.
Przy ustawianiu opcji analizy włączamy filtr wybierając odpowiedni dzień tygodnia - czyli piątek. Brak ustawienia filtru nie generuje błędu a jedynie wyliczenie kolejnych statystyk dla kolejnych dni tygodnia.
Hipotezy:
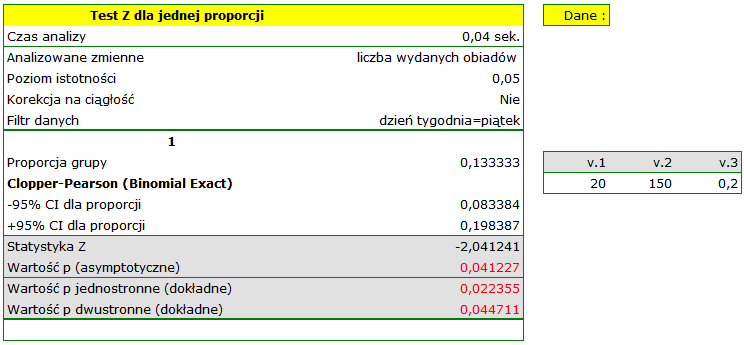
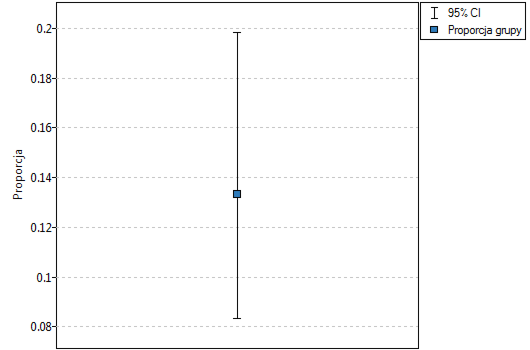
Proporcja wartości wyróżnionych w próbie to 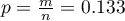 a 95% przedział ufności Cloppera-Pearsona dla tej frakcji
a 95% przedział ufności Cloppera-Pearsona dla tej frakcji 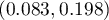 nie zawiera hipotetycznej wartości 0.2.
nie zawiera hipotetycznej wartości 0.2.
Na podstawie testu  bez poprawki na ciągłość (
bez poprawki na ciągłość ( =0.041227) jak i na podstawie dokładnej wartości prawdopodobieństwa wyliczonego z rozkładu dwumianowego (
=0.041227) jak i na podstawie dokładnej wartości prawdopodobieństwa wyliczonego z rozkładu dwumianowego ( =0.044711) moglibyśmy przyjąć (na poziomie istotności
=0.044711) moglibyśmy przyjąć (na poziomie istotności  ), że w piątek wydaje się statystycznie mniej niż
), że w piątek wydaje się statystycznie mniej niż 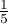 obiadów wydawanych przez cały tydzień. Po zastosowaniu poprawki na ciągłość jednak nie udaje się odrzucić hipotezy zerowej (
obiadów wydawanych przez cały tydzień. Po zastosowaniu poprawki na ciągłość jednak nie udaje się odrzucić hipotezy zerowej ( =0.052479).
=0.052479).
2014/08/22 20:00
2014/08/22 20:00
1)
, 5)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
2)
Wilcoxon F. (1945), Individual comparisons by ranking methods. Biometries 1, 80-83
3)
, 8)
Marascuilo L.A. and McSweeney M. (1977), Nonparametric and distribution-free method for the social sciences. Monterey, CA: Brooks Cole Publishing Company
4)
Fritz C.O., Morris P.E., Richler J.J.(2012), Effect size estimates: Current use, calculations, and interpretation. Journal of Experimental Psychology: General., 141(1):2–18.
6)
Cochran W.G. (1952), The chi-square goodness-of-fit test. Annals of Mathematical Statistics, 23, 315-345
7)
Abdi H. (2007), Bonferroni and Sidak corrections for multiple comparisons, in N.J. Salkind (ed.): Encyclopedia of Measurement and Statistics. Thousand Oaks, CA: Sage
9)
E.B. (1927), Probable Inference, the Law of Succession, and Statistical Inference. Journal of the American Statistical Association: 22(158):209-212
10)
Agresti A., Coull B.A. (1998), Approximate is better than „exact” for interval estimation of binomial proportions. American Statistics 52: 119-126
11)
Clopper C. and Pearson S. (1934), The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 26: 404-413
12)
Brown L.D., Cai T.T., DasGupta A. (2001), Interval Estimation for a Binomial Proportion. Statistical Science, Vol. 16, no. 2, 101-133
statpqpl/porown1grpl.txt · ostatnio zmienione: 2019/12/17 17:27 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


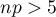 i
i 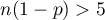 ).
).