Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:survpl
Spis treści
Analiza przeżycia
Analiza przeżycia stosowana często w medycynie, w innych dyscyplinach naukowych występuje pod takimi nazwami jak: analiza niezawodności (ang. reliability analysis), analiza trafności (ang.duration analysis), analiza historii zdarzeń (ang. event history analysis). Jej głównym celem jest ocena czasu przeżycia np. pacjentów po operacji  stosowanym narzędziem są tu tabele trwania życia i krzywe Kaplana-Meiera. Innym interesującym aspektem jest porównanie czasów przeżycia np. czasu przeżycia po zastosowaniu różnych metod leczenia
stosowanym narzędziem są tu tabele trwania życia i krzywe Kaplana-Meiera. Innym interesującym aspektem jest porównanie czasów przeżycia np. czasu przeżycia po zastosowaniu różnych metod leczenia  w tym celu wykorzystywane są metody porównania 2 lub więcej krzywych przeżycia. Opracowano również szereg metod (modeli regresji) pozwalających na badanie wpływu rożnych zmiennych na czas przeżycia.
w tym celu wykorzystywane są metody porównania 2 lub więcej krzywych przeżycia. Opracowano również szereg metod (modeli regresji) pozwalających na badanie wpływu rożnych zmiennych na czas przeżycia.
By ułatwić zrozumienie zagadnienia, podstawowe definicje podane zostaną na przykładzie opisującym długość życia pacjentów po przeszczepie serca:
Zdarzenie - jest to interesująca badacza zmiana np. śmierć;
Czas przeżycia - jest to okres pomiędzy stanem początkowym a wystąpieniem zdarzenia np. długość życia pacjenta po przeszczepie serca;
Uwaga!
W analizie należy zaznaczyć jedną kolumnę z wyliczonym czasem. Gdy dysponujemy dwoma punktami w czasie: punktem początkowym i końcowym przed analizą wyliczamy czas jaki upłynął między tymi punktami korzystając z formuł arkusza
Obserwacje ucięte (ang. censored) - to obserwacje, dla których mamy niepełne informacje o czasie przeżycia.
Obserwacje ucięte i kompletne - przykład dotyczący przeżycia po przeszczepie serca:
- obserwacja kompletna - znana jest data przeszczepu i data śmierci pacjenta, zatem można ustalić dokładny czas przeżycia po przeszczepie;
- obserwacja ucięta prawostronnie - nie jest znana data śmierci pacjenta (chory żyje w chwili ukończenia badania), więc nie można ustalić dokładnego czasu przeżycia;
- obserwacja ucięta lewostronnie - nie jest znana data przeszczepu serca, ale wiadomo, że było to przed rozpoczęciem niniejszego badania, zatem nie można ustalić dokładnego czasu przeżycia.
![LaTeX \begin{pspicture}(-5,-.7)(7,5.6)
\psline{->}(0,0)(0,5)
\psline{->}(0,0)(8.3,0)
\psline{-}(1,0)(1,4.8)
\psline{-}(6,0)(6,4.8)
\psline[linecolor=green, linewidth=2pt]{->}(2,4)(5,4)
\psline[linecolor=red, linewidth=2pt]{->}(1,2.5)(7,2.5)
\psline[linecolor=red, linewidth=2pt]{->}(0.3,1)(4,1)
\rput(1,-.3){początek}
\rput(1,-.7){badania}
\rput(6,-.3){koniec}
\rput(6,-.7){badania}
\rput(8.1,-.3){czas}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img9ad6a304de94e2b2f54799279e2e7879.png)
Uwaga!
Zakończenie badania oznacza zakończenie obserwacji pacjenta, nie zawsze jest to moment zakończenia badania dla wszystkich pacjentów. Zakończeniem badania może być moment w którym tracimy kontakt z pacjentem (nie znamy więc jego czasu przeżycia). Analogicznie rozpoczęcie badania nie musi dotyczyć wszystkich w tym samym czasie.
Tabele przeżycia
Okno z ustawieniami opcji tabel trwania życia wywołujemy poprzez menu Statystyka→Analiza przeżycia→Tabele przeżycia
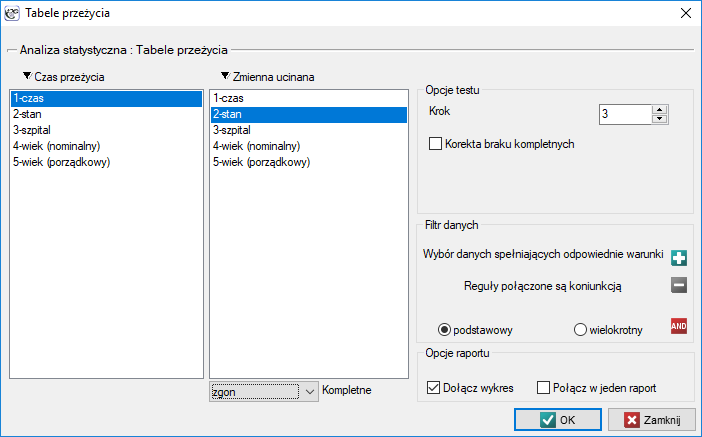
Tabele trwania życia tworzy się dla podanych przez badacza przedziałów czasu przeżycia o równej rozpiętości. Przedziały te można zdefiniować podając krok. Dla każdego przedziału program PQStat wylicza:
- liczbę przypadków wchodzących - liczba osób, które przeżyły do określonego przez przedział czasu;
- liczbę przypadków uciętych - liczba osób w danym przedziale, które są zdefiniowane jako przypadki ucięte;
- liczbę przypadków zagrożonych - liczba przypadków, które wchodzą do danego przedziału minus połowa liczby przypadków uciętych w danym przedziale;
- liczbę przypadków kompletnych - liczba osób, które doświadczyły zdarzenia (czyli zmarły) w danym przedziale;
- proporcje przypadków kompletnych - stosunek liczby przypadków kompletnych (zgonów) w danym przedziale do liczby przypadków zagrożonych w tym przedziale;
- proporcje przypadków przeżywających - oblicza się jako 1 minus proporcja przypadków kompletnych w danym przedziale;
- skumulowane proporcje przeżywających (funkcja przeżycia) - prawdopodobieństwo przeżycia do danego czasu
 ponieważ żeby przeżyć kolejny przedział czasu, trzeba przeżyć wszystkie poprzednie, to prawdopodobieństwo to wyliczane jest jako iloczyn wszystkich poprzednich proporcji przypadków przeżywających;
ponieważ żeby przeżyć kolejny przedział czasu, trzeba przeżyć wszystkie poprzednie, to prawdopodobieństwo to wyliczane jest jako iloczyn wszystkich poprzednich proporcji przypadków przeżywających;
 błąd standardowy funkcji przeżycia;
błąd standardowy funkcji przeżycia;
- gęstość prawdopodobieństwa - oszacowane prawdopodobieństwo doświadczenia zdarzenia (zgonu) w danym przedziale obliczone w jednostce czasu;
 błąd standardowy gęstości prawdopodobieństwa;
błąd standardowy gęstości prawdopodobieństwa;
- stopę hazardu - prawdopodobieństwo (wyliczane na jednostkę czasu) tego, że przypadek, który przeżył do początku danego przedziału doświadczy w tym przedziale zdarzenia (zgonu);
 błąd standardowy stopy hazardu.
błąd standardowy stopy hazardu.
Uwaga!
W przypadku braku obserwacji kompletnych w dowolnym przedziale czasu przeżycia istnieje możliwość zastosowania korekty. Zerową liczbę przypadków kompletnych zastępuje się wówczas wartością 0.5.
Interpretacja graficzna
Dla zobrazowania informacji uzyskanych dzięki tabelom przeżycia możemy posłużyć się kilkoma wykresami:
- wykresem funkcji przeżycia,
- wykresem gęstości prawdopodobieństwa,
- wykresem stopy hazardu.
Przykład (plik przeszczep.pqs)
Badano długość życia chorych po przeszczepie wątroby. Przez okres 21 lat poddano obserwacji grupę 89 pacjentów, których wiek w chwili przeszczepu należał do przedziału 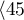 lat
lat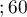 lat
lat . Fragment zebranych danych przedstawia poniższa tabela:
. Fragment zebranych danych przedstawia poniższa tabela:
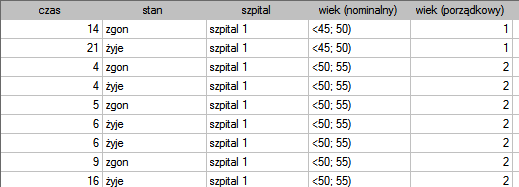
Dane kompletne w tej analizie to te, o których mamy pełną informację o długości życia po przeszczepie, czyli opisane jako „zgon” (są to 53 osoby, co stanowi 59.55%). Dane ucięte to te, o których tej informacji nie mamy ponieważ w chwili zakończenia badania żyją (jest to 36 osób, co stanowi 40.45%). Budujemy tablice trwania życia tych pacjentów tworząc 3 letnie przedziały czasowe:
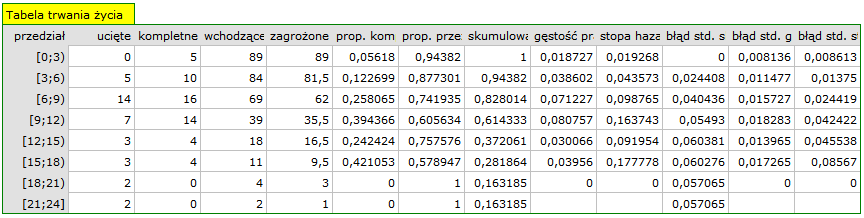
Dla każdego 3-letniego przedziału możemy zinterpretować uzyskane w tabeli wyniki - przykładowo dla osób, które żyją przynajmniej 9 lat od przeszczepu, a zatem weszły do przedziału [9;12):
- liczba osób, które przeżyły do 9 lat od przeszczepu to 39;
- jest 7 osób, o których wiemy, że żyły przynajmniej 9-12 lat - gdy informacje o nich były zbierane, ale nie wiemy czy żyły dłużej, gdyż po tym czasie wypadły z badania;
- liczbę osób zagrożonych zgonem w tym przedziale to 36;
- jest 14 osób, o których wiemy, że zmarły od 9 do 12 lat po przeszczepie;
- 39.4% narażonych pacjentów zmarło 9-12 lat po przeszczepie;
- 60.6% narażonych pacjentów żyło 9-12 lat po przeszczepie;
- procent przeżywających do 9 lat po przeszczepie to 61.4%
 5%
5% - 0.08
 0.02 - to prawdopodobieństwo zgonu dla każdego roku z przedziału 9-12
0.02 - to prawdopodobieństwo zgonu dla każdego roku z przedziału 9-12 - 0.16
 0.04 - to warunkowe, roczne prawdopodobieństwo zgonu dla przypadku, który przeżył do początku przedziału 9-12;
0.04 - to warunkowe, roczne prawdopodobieństwo zgonu dla przypadku, który przeżył do początku przedziału 9-12;
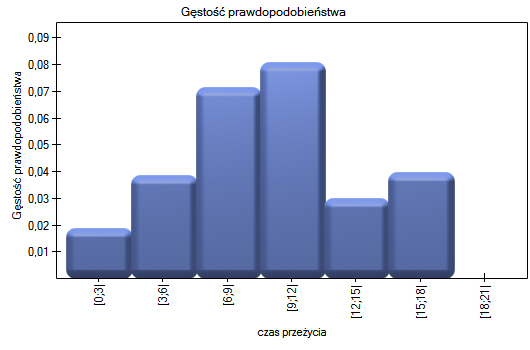
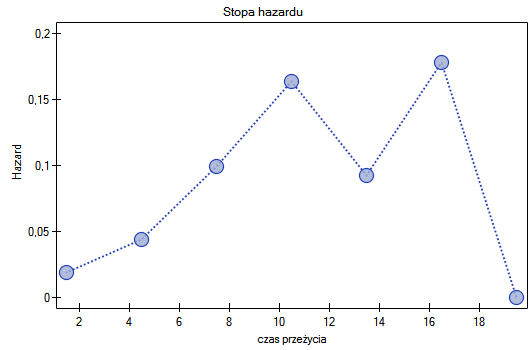
Wyniki przedstawimy na kilku wykresach:
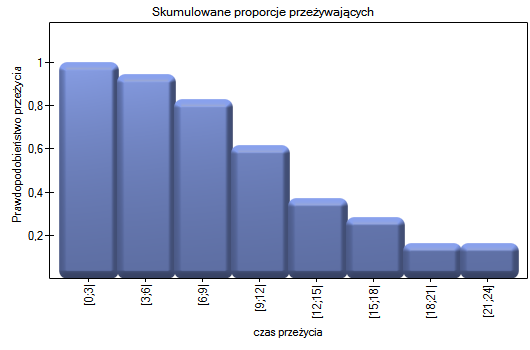
Prawdopodobieństwo przeżycia maleje wraz z upływem czasu jaki minął od przeszczepu. Nie obserwujemy jednak nagłego spadku funkcji przeżycia, a więc czasu w który gwałtownie wzrastałoby prawdopodobieństwo zgonu.
2014/08/24 23:44
· admin
Krzywe Kaplana-Meiera
 Krzywe Kaplana-Meiera pozwalają na ocenę czasu przeżycia bez konieczności arbitralnego grupowania obserwacji, tak jak to jest w tabelach przeżycia. Estymator ten został wprowadzony przez Kaplana i Meiera (1958)1).
Krzywe Kaplana-Meiera pozwalają na ocenę czasu przeżycia bez konieczności arbitralnego grupowania obserwacji, tak jak to jest w tabelach przeżycia. Estymator ten został wprowadzony przez Kaplana i Meiera (1958)1).
Okno z ustawieniami opcji krzywej Kaplana-Meiera wywołujemy poprzez menu Statystyka→Analiza przeżycia→Analiza Kaplana-Meiera
Podobnie jak dla tablic przeżycia, wyliczamy tutaj funkcję przeżycia, czyli prawdopodobieństwo przeżycia do danego czasu. Wykres funkcji przeżycia Kaplana-Meiera tworzy funkcja schodkowa. Na podstawie błędu standardowego (formuła Greenwooda) i transformacji logarytmicznej (log-log) zbudowane są przedziały ufności wokół tej krzywej. Punkt czasu, przy którym wartość funkcji przyjmuje 0.5, to mediana czasu przeżycia. Mediana ta wskazuje na 50% ryzyko wystąpienia zgonu, czyli przewiduje iż u połowy pacjentów nastąpi zgon w ciągu wskazanego czasu. Zarówno mediana jak i inne percentyle wyznaczane są jako najkrótszy czas przeżycia, dla którego funkcja przeżycia jest mniejsza lub równa danemu percentylowi. Dla mediany wyznaczany jest przedział ufności w oparciu o metodę test-based autorstwa Brookmeyer i Crowley (1982)2). Średnia czasu przeżycia jest wyznaczona jako pole pod krzywą przeżycia.
Dane dotyczące czasu przeżycia są zwykle mocno skośne, dlatego w analizie przeżycia, mediana jest lepszą miarą tendencji centralnej niż średnia.
Przykład c.d. (plik przeszczep.pqs)
Przedstawimy długość życia po przeszczepie wątroby przy pomocy krzywej Kaplana-Meiera
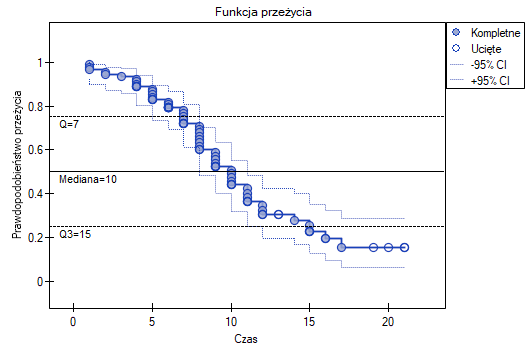

Funkcja przeżycia nie opada gwałtownie zaraz po przeszczepie. Wnioskujemy stąd, że początkowy okres po transplantacji nie jest szczególnie obarczony ryzykiem zgonu. Z wartości mediany wynika, że w ciągu 10 lat od przeszczepu oczekujemy, że u połowy pacjentów nastąpi zgon. Wartość tę zaznaczamy na wykresie rysując linię w punkcie 0.5 oznaczającym medianę. W podobny sposób zaznaczamy na wykresie kwartyle.
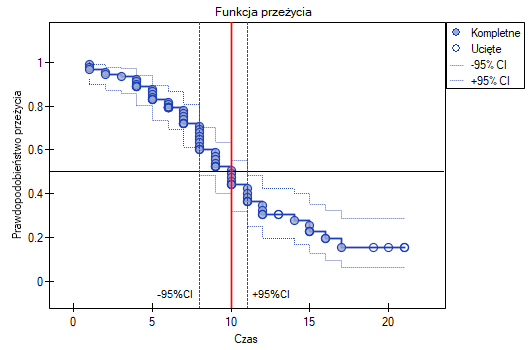
Przedział ufności dla mediany możemy zobrazować na wykresie wyrysowując linie pionowe w oparciu o przedział ufności wokół krzywej oraz linie na poziomie 0.5.
2014/08/24 23:44
· admin
Porównywanie krzywych przeżycia
Funkcje przeżycia mogą być budowane oddzielnie dla różnych podgrup np. oddzielnie dla kobiet i mężczyzn, a następnie porównane między sobą. Takie porównanie może dotyczyć zarówno dwóch, jak i kilku krzywych.
Okno z ustawieniami opcji porównania krzywych przeżycia wywołujemy poprzez menu Statystyka→Analiza przeżycia→Porównanie grup
Porównania  krzywych przeżycia
krzywych przeżycia 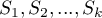 w poszczególnych punktach czasu przeżycia
w poszczególnych punktach czasu przeżycia  w programie możemy dokonać przy pomocy trzech testów:
w programie możemy dokonać przy pomocy trzech testów:
Testu log-rank najbardziej znanego i szeroko stosowanego, nawiązującego do procedury Mantela-Heanszela dla wielu tabel 2×2 (Mantel-Heanszel 19593), Mantel 19664), Cox 19725)),
Uogólnienia Gehana testu Wilcoxona wywodzącego się od testu Wilcoxona (Breslow 1970, Gehan 19656)7)),
Testu Taron-Ware wywodzącego się od testu Wilcoxona (Tarone i Ware 19778)).
Wszystkie trzy testy działają w oparciu o tę samą statystykę testową, inne są tylko wagi 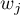 w poszczególnych punktach osi czasu, na których bazuje statystyka testowa.
w poszczególnych punktach osi czasu, na których bazuje statystyka testowa.
Test log-rank: 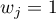 - wszystkie punkty osi czasu posiadają tę samą wagę, co daje większy wpływ na uzyskany wynik późniejszym wartościom osi czasu;
- wszystkie punkty osi czasu posiadają tę samą wagę, co daje większy wpływ na uzyskany wynik późniejszym wartościom osi czasu;
Uogólnienie Gehana testu Wilcoxona:  - momenty czasowe są ważone liczbą obserwacji w każdym z nich, a zatem przypisywane są większe wagi początkowym wartościom osi czasu;
- momenty czasowe są ważone liczbą obserwacji w każdym z nich, a zatem przypisywane są większe wagi początkowym wartościom osi czasu;
Test Taron-Ware: 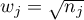 - momenty czasowe są ważone pierwiastkiem z liczby obserwacji w każdym z nich co powoduje, usytuowanie tego testu pomiędzy dwoma omówionymi wcześniej.
- momenty czasowe są ważone pierwiastkiem z liczby obserwacji w każdym z nich co powoduje, usytuowanie tego testu pomiędzy dwoma omówionymi wcześniej.
Ważnym warunkiem stosowania powyższych testów jest proporcjonalność hazardu. Hazard definiowany jako nachylenie krzywej przeżycia jest miarą tego, jak szybko następuje niepożądane zdarzenie. Złamanie założenia proporcjonalności hazardu choć nie dyskwalifikuje całkowicie powyższych testów, to niesie kilka niebezpieczeństw. Przede wszystkim położenie punktu przecięcia krzywych względem osi czasu ma decydujący wpływ na obniżenie mocy poszczególnych testów.
Przykład c.d. (plik przeszczep.pqs)
Różnice w krzywych przeżycia
Hipotezy:
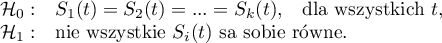
W obliczeniach wykorzystano statystykę chi-kwadrat postaci:
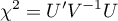 gdzie:
gdzie:
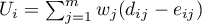
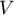 - macierz kowariancji o wymiarach
- macierz kowariancji o wymiarach 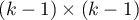
gdzie:
diagonala: 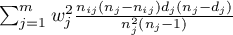 ,
,
poza diagonalą (off diagonal): 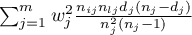
 - liczba momentów czasowych, w których nastąpiło niepożądane zdarzenie (zgon),
- liczba momentów czasowych, w których nastąpiło niepożądane zdarzenie (zgon),
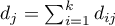 - obserwowana liczba niepożądanych zdarzeń (zgonów) w
- obserwowana liczba niepożądanych zdarzeń (zgonów) w  -tym momencie czasowym,
-tym momencie czasowym,
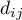 - obserwowana liczba niepożądanych zdarzeń (zgonów) w
- obserwowana liczba niepożądanych zdarzeń (zgonów) w  -tej grupie w
-tej grupie w  -tym momencie czasowym,
-tym momencie czasowym,
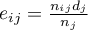 - oczekiwana liczba niepożądanych zdarzeń (zgonów) w
- oczekiwana liczba niepożądanych zdarzeń (zgonów) w  -tej grupie w
-tej grupie w  -tym momencie czasowym,
-tym momencie czasowym,
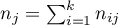 - liczba narażonych w
- liczba narażonych w  -tym momencie czasowym.
-tym momencie czasowym.
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z 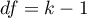 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Iloraz Hazardów
W teście Log-rank dla każdej grupy podawane są obserwowane wartości niepożądanych zdarzeń (zgonów) 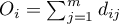 oraz odpowiednie wartości oczekiwane
oraz odpowiednie wartości oczekiwane 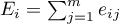 .
.
Miarą opisującą wielkość obserwowanej różnicy między parą krzywych przeżycia jest Iloraz Hazardów (ang. Hazard Ratio - 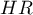 ).
).
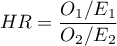
Jeśli Iloraz Hazardów jest większy niż 1 np. 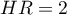 , to stopień narażenia na niepożądane zdarzenie w pierwszej grupie jest dwa razy większy niż w grupie drugiej. Odwrotna sytuacja jest gdy
, to stopień narażenia na niepożądane zdarzenie w pierwszej grupie jest dwa razy większy niż w grupie drugiej. Odwrotna sytuacja jest gdy 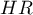 jest mniejsze niż jeden. Natomiast przy
jest mniejsze niż jeden. Natomiast przy 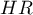 równym 1 obie grupy są narażone w tym samym stopniu.
równym 1 obie grupy są narażone w tym samym stopniu.
Uwaga!
Przedział ufności dla 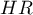 wyliczany jest w oparciu o błąd standardowy logarytmu
wyliczany jest w oparciu o błąd standardowy logarytmu 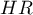 (Armitage i Berry 19949)).
(Armitage i Berry 19949)).
Przykład c.d. (plik przeszczep.pqs)
2014/08/22 20:00
Trend w krzywych przeżycia
Hipotezy:
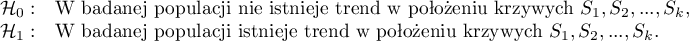
W obliczeniach wykorzystano statystykę chi-kwadrat postaci:
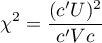
gdzie:
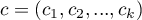
 wektor wag dla porównywanych grup informujący o ich naturalnym porządku (najczęściej kolejne liczby naturalne).
wektor wag dla porównywanych grup informujący o ich naturalnym porządku (najczęściej kolejne liczby naturalne).
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z jednym stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
By można było przeprowadzić analizę trendu w krzywych przeżycia, zmienna grupująca musi być zmienną liczbową, w której wartości liczb informują o naturalnym porządku grup. Liczby te w analizie traktowane są jako wagi 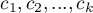 .
.
Przykład c.d. (plik przeszczep.pqs)
2014/08/22 20:00
Krzywe przeżycia dla warstw
Często chcąc porównać czasy przeżycia dla dwóch lub więcej grup nie możemy zapomnieć o innych czynnikach, które mogą mieć wpływ na wynik tego porównania. Dostosowanie (korekcja) analizy o takie czynniki może być przydatna. Na przykład w badaniach domu opieki porównujących długość pobytu osób poniżej i powyżej 80 roku życia uzyskano istotną różnicę. Wiadomo jednak, że płeć ma silny związek z długością pobytu, a także wiekiem. Dlatego próbując ocenić wpływ wieku dobrym pomysłem byłaby stratyfikacja analizy ze względu na płeć.
Hipotezy dla różnic w krzywych przeżycia:
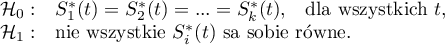
Hipotezy dla analizy trendu w krzywych przeżycia:
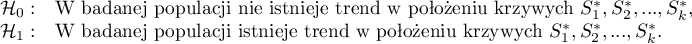
gdzie 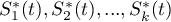 -to krzywe przeżycia po korekcji o zmienną wyznaczającą warstwy.
-to krzywe przeżycia po korekcji o zmienną wyznaczającą warstwy.
Obliczenia dla statystyk testowych bazują na formułach opisanych dla testów nie uwzględniających warstw z tą różnicą, że macierz U i V jest zastąpiona sumą macierzy 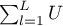 i
i 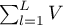 . Sumowanie następuje po warstwach utworzonych przez zmienną, względem której dostosowujemy (korygujemy) analizę (adjusted) l={1,2,…,L}
. Sumowanie następuje po warstwach utworzonych przez zmienną, względem której dostosowujemy (korygujemy) analizę (adjusted) l={1,2,…,L}
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przykład c.d. (plik przeszczep.pqs)
Różnice dla dwóch krzywych przeżycia
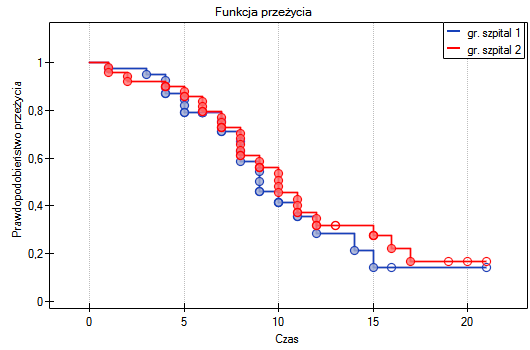
Przeszczepy wątroby dokonywane były w dwóch różnych szpitalach. Sprawdzimy, czy długość życia pacjentów po przeszczepie zależały od szpitala, w którym dokonywano przeszczepu. Porównania krzywych przeżycia dla tych szpitali dokonamy w oparciu o wszystkie zaproponowane w programie testy służące temu porównaniu.
Hipotezy:
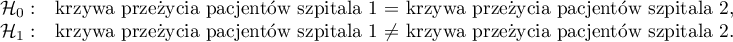

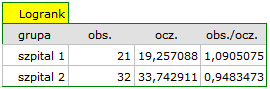
Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość  =0.6004 dla testu log-rank (p=0.6959 dla Gehana i 0.6465 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę
=0.6004 dla testu log-rank (p=0.6959 dla Gehana i 0.6465 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę  . Długość życia wyliczona dla pacjentów obu tych szpitali jest podobna.
. Długość życia wyliczona dla pacjentów obu tych szpitali jest podobna.
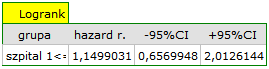
Do tego samego wniosku dojdziemy porównując ryzyko zgonu dla tych szpitali poprzez wyznaczenie ilorazu tego ryzyka. Uzyskana oszacowana wartość 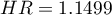 , a 95% przedział ufności dla tej wartości zawiera jedynkę:
, a 95% przedział ufności dla tej wartości zawiera jedynkę:  0.6570, 2.0126
0.6570, 2.0126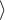 .
.
Różnice dla wielu krzywych przeżycia
Przeszczepy wątroby dokonywane były u ludzi w różnym wieku. Wyróżniono 3 grupy wiekowe: 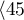 lat
lat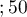 lat
lat ,
, 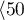 lat
lat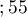 lat
lat ,
, 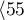 lat
lat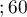 lat
lat . Sprawdzimy, czy długość życia pacjentów po przeszczepie zależy od ich wieku w chwili dokonania przeszczepu.
. Sprawdzimy, czy długość życia pacjentów po przeszczepie zależy od ich wieku w chwili dokonania przeszczepu.
Hipotezy:
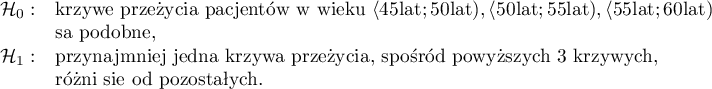
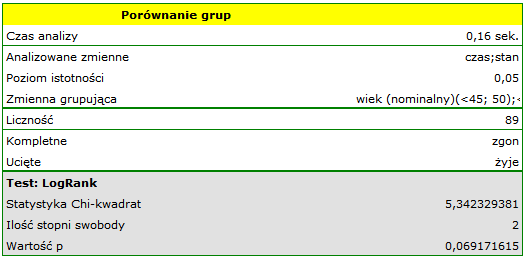
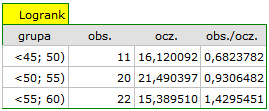
Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość  =0.0692 w teście log-rank (p=0.09279 dla Gehana, p=0.0779 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę
=0.0692 w teście log-rank (p=0.09279 dla Gehana, p=0.0779 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę  . Długość życia wyliczona dla pacjentów należących do porównywanych trzech grup wiekowych jest podobna. Choć należy zauważyć że wartości p są dość bliskie standardowemu poziomowi istotności 0.05.
. Długość życia wyliczona dla pacjentów należących do porównywanych trzech grup wiekowych jest podobna. Choć należy zauważyć że wartości p są dość bliskie standardowemu poziomowi istotności 0.05.
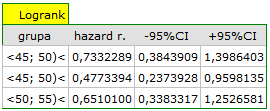
Przeglądając wartości hazardu (ilorazu wartości obserwowanych i oczekiwanych niepożądanych zdarzeń) zauważamy, że z każdą kategorią wiekową są one nieco wyższe  0.68, 0.93, 1.43
0.68, 0.93, 1.43 . Chociaż nie wykryto istotnych statystycznie różnic między nimi, to możliwe jest, że znaleziony zostanie trend wzrostu wartości hazardu (trend w położeniu krzywych przeżycia).
. Chociaż nie wykryto istotnych statystycznie różnic między nimi, to możliwe jest, że znaleziony zostanie trend wzrostu wartości hazardu (trend w położeniu krzywych przeżycia).
Trend dla kilku krzywych przeżycia
Jeśli do testu wprowadzimy informację dotyczącą uporządkowania porównywanych kategorii (wykorzystamy zmienną wiek, w której przedziały wiekowe ponumerujemy odpowiednio 1, 2 i 3), wówczas będziemy mogli sprawdzić, czy istnieje trend w porównywanych krzywych. Będziemy badać hipotezy:


Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
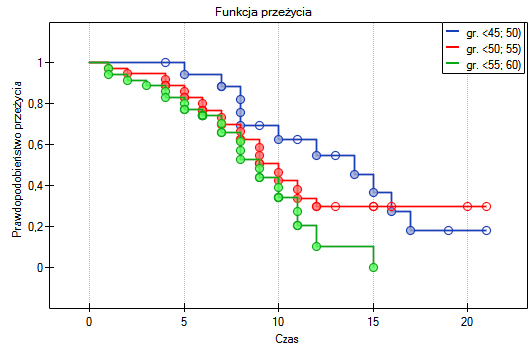
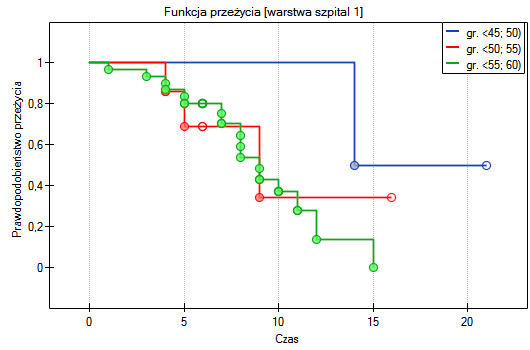
, w oparciu o uzyskaną wartość  =0.0237 w teście log-rank (p=0.0317 dla Gehana, p=0.0241 dla Tarona) wnioskujemy, że krzywe przeżycia ułożone są w pewnym trendzie. Najniżej na wykresie Kaplana-Meiera znajduje się krzywa dla osób w wieku
=0.0237 w teście log-rank (p=0.0317 dla Gehana, p=0.0241 dla Tarona) wnioskujemy, że krzywe przeżycia ułożone są w pewnym trendzie. Najniżej na wykresie Kaplana-Meiera znajduje się krzywa dla osób w wieku  55 lat; 60 lat). Nad nią jest krzywa dla pacjentów w wieku
55 lat; 60 lat). Nad nią jest krzywa dla pacjentów w wieku  50 lat; 55 lat). Najwyżej zaś krzywa dla pacjentów w wieku
50 lat; 55 lat). Najwyżej zaś krzywa dla pacjentów w wieku  45 lat; 50 lat). Zatem czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu.
45 lat; 50 lat). Zatem czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu.
Krzywe przeżycia dla warstw
Sprawdzimy teraz, czy obserwowany wcześniej trend jest niezależny od szpitala w którym dokonano przeszczepu. W tym celu jako zmienną warstwa wybierzemy szpital.
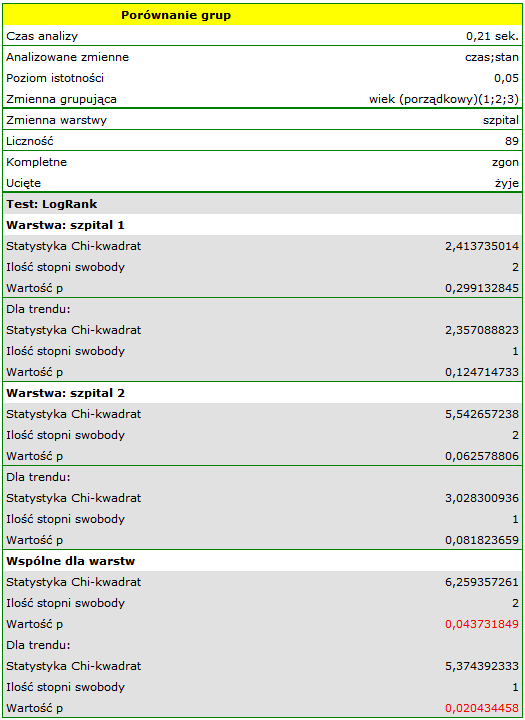
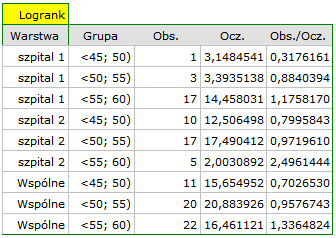
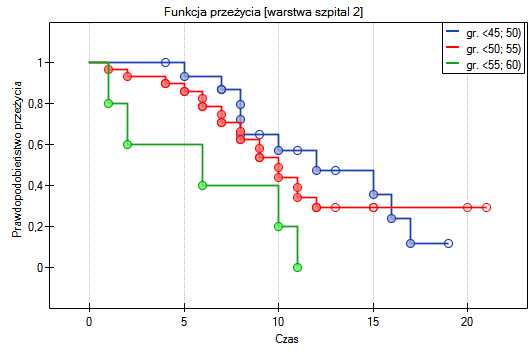
W raporcie najpierw przedstawiona jest analiza poszczególnych warstw, zarówno wyniki testów jak i wartości hazardu. W warstwie pierwszej trend wzrostu hazardu jest widoczny, choć nieistotny, trend o tym samym kierunku (wynik na pograniczu istotności statystycznej) obserwowany jest w warstwie drugiej. Kumulacja tych trendów we wspólnej analizie warstw pozwoliła uzyskać istotność trendu krzywych przeżycia. Zatem: czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu niezależnie od szpitala dokonującego przeszczepu.
Analiza porównawcza krzywych przeżycia w korekcji o warstwy daje wynik istotny dla testu log-rank i Tarona a nieistotny dla Gehana, co może wskazywać na to, że pojawiające się różnice w krzywych nie są tak widoczne w początkowych okresach czasu przeżycia co w okresach późniejszych. Przyglądając się ilorazowi hazardu dla porównywanych parami krzywych
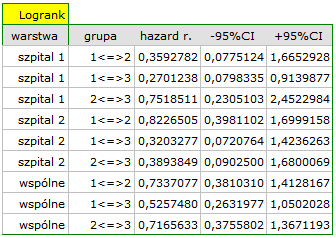
możemy zlokalizować istotne różnice. Najmniejszy iloraz hazardu mamy dla porównania krzywej dla najmłodszej grupy z krzywą dla grupy najstarszej 0.53, 95% przedział ufności dla tego ilorazu  0.26 ; 1.05
0.26 ; 1.05 zawiera co prawda wartość 1, ale jest na pograniczu tej wartości, co może sugerować wystąpienie między odpowiadającymi im krzywymi istotnych różnic. By potwierdzić to przypuszczenie dociekliwy badacz, używając filtru danych w oknie analizy, może porównać krzywe parami.
zawiera co prawda wartość 1, ale jest na pograniczu tej wartości, co może sugerować wystąpienie między odpowiadającymi im krzywymi istotnych różnic. By potwierdzić to przypuszczenie dociekliwy badacz, używając filtru danych w oknie analizy, może porównać krzywe parami.

Należy jednak pamiętać by zastosować jedną z poprawek używanych przy wielokrotnych porównaniach i zmodyfikować poziom istotności. W tym przypadku dla poprawki Bonferroniego przy trzech porównaniach poziom istotności wyniesie 0.017. Dla uproszczenia rozważań posłużymy się tylko testem log-rank.
 45 lat; 50 lat) vs
45 lat; 50 lat) vs  50 lat; 55 lat)
50 lat; 55 lat)

 45 lat; 50 lat) vs
45 lat; 50 lat) vs  55 lat; 60 lat)
55 lat; 60 lat)

 50 lat; 55 lat) vs
50 lat; 55 lat) vs  55 lat; 60 lat)
55 lat; 60 lat)

Zgodnie z oczekiwaniem istotne statystycznie różnice dotyczą tylko krzywych przeżycia dla najmłodszej i najstarszej grupy wiekowej.
2014/08/22 20:00
2014/08/22 20:00
Regresja proporcjonalnego hazardu Cox'a
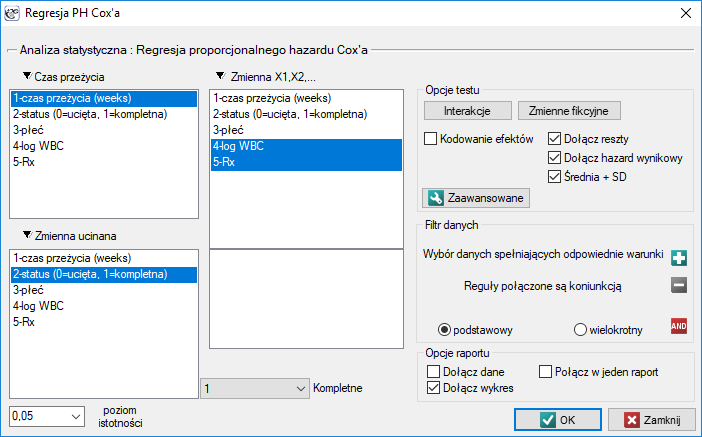
Okno z ustawieniami opcji Regresji Cox'a wywołujemy poprzez menu Statystyka→Analiza przeżycia→Regresja PH Cox'a
Regresja Cox'a, znana również jako model proporcjonalnego hazardu Cox'a (Cox PH model) - Cox D.R. (1972)10), jest najszerzej stosowanym podejściem regresyjnym w analizie przeżycia. Pozwala na zbadanie wpływu wielu zmiennych niezależnych ( ,
,  ,
,  ,
, 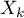 ) na czas przeżycia. Jest to podejście w pewnym sensie nieparametryczne, a więc obarczone niewieloma założeniami - stąd też wynika jego popularność. Nie musi być znana natura ani kształt funkcji hazardu czy przeżycia, a najważniejszy warunek to założenie, które dotyczy również większości parametrycznych modeli przeżycia czyli proporcjonalność hazardu.
) na czas przeżycia. Jest to podejście w pewnym sensie nieparametryczne, a więc obarczone niewieloma założeniami - stąd też wynika jego popularność. Nie musi być znana natura ani kształt funkcji hazardu czy przeżycia, a najważniejszy warunek to założenie, które dotyczy również większości parametrycznych modeli przeżycia czyli proporcjonalność hazardu.
Funkcja, na której oparty jest model proporcjonalnego hazardu Cox'a opisuje hazard wynikowy i jest produktem dwóch wielkości, z których tylko jedna jest zależna od czasu ( ):
):
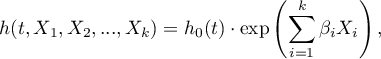 gdzie:
gdzie:
- [
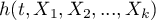 ] - wynikowy hazard opisujący zmieniające się w czasie ryzyko zależne od innych czynników np. sposobu leczenia,
] - wynikowy hazard opisujący zmieniające się w czasie ryzyko zależne od innych czynników np. sposobu leczenia, - [
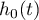 ] - hazard bazowy, czyli hazard przy założeniu, że wszystkie zmienne objaśniające są równe zero,
] - hazard bazowy, czyli hazard przy założeniu, że wszystkie zmienne objaśniające są równe zero,
- [
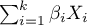 ] - kombinacja (najczęściej liniowa) zmiennych niezależnych i parametrów modelu,
] - kombinacja (najczęściej liniowa) zmiennych niezależnych i parametrów modelu,
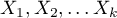 - zmienne objaśniające, niezależne od czasu,
- zmienne objaśniające, niezależne od czasu,
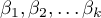 - parametry.
- parametry.
Zmienne fikcyjne i interakcje w modelu
Omówienie przygotowania zmiennych fikcyjnych i interakcji przedstawiono w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
Korekcja rang wiązanych w regresji Cox'a oparta jest na metodzie Breslow'a11)
Model można sprowadzić do postaci liniowej:
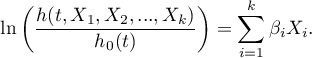
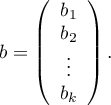
Rozwiązaniem równania jest wówczas wektor ocen parametrów  nazywanych współczynnikami regresji:
nazywanych współczynnikami regresji:
Współczynniki te szacowane są poprzez tzw. „częściową” metodę największej wiarygodności. Jest to metoda „częściowa” ponieważ poszukiwanie maksimum funkcji wiarygodności  (w programie użyto algorytm iteracyjny Newton-Raphson) odbywa się tylko dla danych kompletnych, dane ucięte są w tym algorytmie uwzględniane, ale nie bezpośrednio.
(w programie użyto algorytm iteracyjny Newton-Raphson) odbywa się tylko dla danych kompletnych, dane ucięte są w tym algorytmie uwzględniane, ale nie bezpośrednio.
Każdy współczynnik obarczony jest pewnym błędem szacunku. Wielkość tego błędu wyliczana jest ze wzoru:
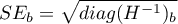
gdzie:
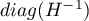 to główna przekątna macierzy kowariancji.
to główna przekątna macierzy kowariancji.
Uwaga!
Budując model należy pamiętać, że liczba obserwacji powinna być dziesięciokrotnie większa lub równa stosunkowi liczby szacowanych parametrów modelu ( ) i mniejszej z proporcji liczności uciętych lub kompletnych (
) i mniejszej z proporcji liczności uciętych lub kompletnych ( ), czyli (
), czyli (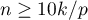 ), Peduzzi P. i inni (1995)12).
), Peduzzi P. i inni (1995)12).
Uwaga! Budując model należy pamiętać, że zmienne niezależne nie powinny być współliniowe. W przypadku gdy występuje współliniowość, estymacja może być niepewna a uzyskane wartości błędów bardzo wysokie.
Uwaga! Kryterium zbieżności funkcji algorytmu iteracyjnego Newtona-Raphsona można kontrolować przy pomocy dwóch parametrów: limitu iteracji zbieżności (podaje maksymalną ilość iteracji w jakiej algorytm powinien osiągnąć zbieżność) i kryterium zbieżności (podaje wartość poniżej której uzyskana poprawa estymacji uznana będzie za nieznaczną i algorytm zakończy działanie).
Przykład c.d. (plik: remisjaBiałaczka.pqs)
Iloraz Hazardu (HR)
Dla każdej zmiennej niezależnej wyliczany jest jednostkowy Iloraz Hazardu (ang. Hazard Ratio - 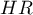 ):
):
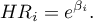 Wyraża on zmianę ryzyka niepożądanego zdarzenia, gdy zmienna niezależna rośnie o 1 jednostkę. Wynik ten jest skorygowany o pozostałe zmienne niezależne znajdujące się w modelu w ten sposób, że zakłada iż pozostają one na stałym poziomie podczas, gdy badana zmienna niezależna rośnie o jednostkę.
Wyraża on zmianę ryzyka niepożądanego zdarzenia, gdy zmienna niezależna rośnie o 1 jednostkę. Wynik ten jest skorygowany o pozostałe zmienne niezależne znajdujące się w modelu w ten sposób, że zakłada iż pozostają one na stałym poziomie podczas, gdy badana zmienna niezależna rośnie o jednostkę.
Wartość 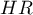 interpretujemy następująco:
interpretujemy następująco:
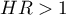 oznacza stymulujący wpływ badanej zmiennej niezależnej na wystąpienie niepożądanego zdarzenia, tj. mówi o ile wzrasta ryzyko na wystąpienie niepożądanego zdarzenia, gdy zmienna niezależna wzrasta o jeden poziom.
oznacza stymulujący wpływ badanej zmiennej niezależnej na wystąpienie niepożądanego zdarzenia, tj. mówi o ile wzrasta ryzyko na wystąpienie niepożądanego zdarzenia, gdy zmienna niezależna wzrasta o jeden poziom.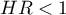 oznacza destymulujący wpływ badanej zmiennej niezależnej na wystąpienie niepożądanego zdarzenia, tj. mówi o ile spada ryzyko na wystąpienie niepożądanego zdarzenia, gdy zmienna niezależna wzrasta o jeden poziom.
oznacza destymulujący wpływ badanej zmiennej niezależnej na wystąpienie niepożądanego zdarzenia, tj. mówi o ile spada ryzyko na wystąpienie niepożądanego zdarzenia, gdy zmienna niezależna wzrasta o jeden poziom.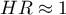 oznacza, że badana zmienna niezależna nie ma wpływu na wystąpienie niepożądanego zdarzenia.
oznacza, że badana zmienna niezależna nie ma wpływu na wystąpienie niepożądanego zdarzenia.
Uwaga!
Jeśli analizę przeprowadzamy dla modelu innego niż liniowy, lub uwzględniamy interakcję, wówczas analogicznie jak w modelu regresji logistycznej na podstawie ogólnego wzoru możemy wyliczyć odpowiedni  zmieniając formułę będącą kombinacją zmiennych niezależnych.
zmieniając formułę będącą kombinacją zmiennych niezależnych.
Przykład c.d. (plik: remisjaBiałaczka.pqs)
2014/08/22 20:00
Weryfikacja modelu
Istotność statystyczna poszczególnych zmiennych w modelu (istotność ilorazu hazardów)
Na podstawie współczynnika oraz jego błędu szacunku możemy wnioskować czy zmienna niezależna, dla której ten współczynnik został oszacowany wywiera istotny wpływ na zmienną zależną. W tym celu posługujemy się testem Walda.
Hipotezy:
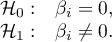
lub równoważnie:
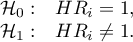
Statystykę testową testu Walda wyliczamy według wzoru:
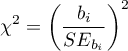
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniem swobody .
stopniem swobody .
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Jakość zbudowanego modelu
Dobry model powinien spełniać dwa podstawowe warunki: powinien być dobrze dopasowany i możliwie jak najprostszy. Jakość modelu proporcjonalnego hazardu Cox'a możemy ocenić kilkoma ogólnymi miarami, które opierają się na:
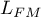 - maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
- maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
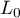 - maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
- maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
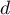 - obserwowanej liczbie niepożądanych zdarzeń.
- obserwowanej liczbie niepożądanych zdarzeń.
Kryteria informacyjne opierają się na entropii informacji niesionej przez model (niepewności modelu) tzn. szacują utraconą informację, gdy dany model jest używany do opisu badanego zjawiska. Powinniśmy zatem wybierać model o minimalnej wartości danego kryterium informacyjnego.
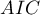 ,
, 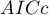 i
i 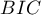 jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby parametrów w modelu (
jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby parametrów w modelu ( ) i liczby obserwacji kompletnych (
) i liczby obserwacji kompletnych (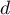 ). W obu przypadkach element ten rośnie wraz ze wzrostem liczby parametrów i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
). W obu przypadkach element ten rośnie wraz ze wzrostem liczby parametrów i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
- Kryterium informacyjne Akaikego (ang. Akaike information criterion)
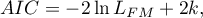
Jest to kryterium asymptotyczne - odpowiednie dla dużych prób.
- Poprawione kryterium informacyjne Akaikego
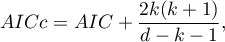
Poprawka kryterium Akaikego dotyczy wielkości próby (liczby zdarzeń niepożądanych), przez co jest to miara rekomendowana również dla prób o małych licznościach.
- Bayesowskie kryterium informacyjne Schwartza (ang. Bayes Information Criterion lub Schwarz criterion)
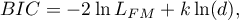
Podobnie jak poprawione kryterium Akaikego uwzględnia wielkość próby (liczbę zdarzeń niepożądanych) - Volinsky i Raftery 2000r13)
Pseudo R - tzw. McFadden
- tzw. McFadden  jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej
jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej  wyznaczanego dla liniowej regresji wielorakiej).
wyznaczanego dla liniowej regresji wielorakiej).
Wartość tego współczynnika mieści się w przedziale 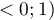 , gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu,
, gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu, 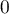 - zupełny bark dopasowania. Współczynnik
- zupełny bark dopasowania. Współczynnik 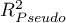 wyliczamy z wzoru:
wyliczamy z wzoru:
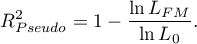
Ponieważ współczynnik 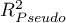 nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
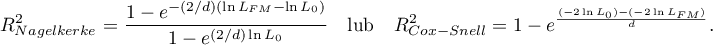
Istotność statystyczna wszystkich zmiennych w modelu
Podstawowym narzędziem szacującym istotność wszystkich zmiennych w modelu jest test ilorazu wiarygodności. Test ten weryfikuje hipotezę:
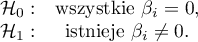
Statystyka testowa ma postać:
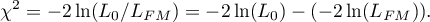
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

AUC – pole pod krzywą ROC – Krzywa ROC – zbudowana na podstawie informacji o wystąpieniu zdarzenia lub jego braku oraz kombinacji zmiennych niezależnych i parametrów modelu – pozwala na ocenę zdolności zbudowanego modelu regresji Cox'a do klasyfikacji przypadków do dwóch grup: (1 – zdarzenie) i (0 – brak zdarzenia). Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną modelu. Gdy krzywa ROC pokrywa się z przekątną  , to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej
, to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej  , czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą
, czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą  , zatem większe niż
, zatem większe niż 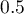
Hipotezy:
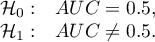
Statystyka testowa ma postać:
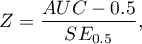 gdzie:
gdzie:
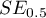 - błąd pola.
- błąd pola.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo, dla krzywej ROC podawana jest proponowana wartość punktu odcięcia kombinacji zmiennych niezależnych i parametrów modelu.
Przykład c.d. (plik: remisjaBiałaczka.pqs)
2014/08/22 20:00
Analiza reszt modelu
Analiza reszt modelu pozwala na weryfikację jego założeń. Głównym jej celem w regresji Cox'a jest lokalizacja wartości odstających i badanie proporcjonalności hazardu. Standardowo w modelach regresji reszty oblicza się jako różnice obserwowanych i przewidywanych przez model wartości zmiennej zależnej. Jednakże w przypadku występowania zmiennych uciętych taka koncepcja wyznaczania reszt nie jest odpowiednia. W programie można analizować reszty opisywane jako: Martingale, Deviance, Schoenfeld. Reszty te można wyrysowywać względem czasu lub zmiennych niezależnych.
Założenie proporcjonalności hazardu
Opracowano szereg graficznych metod pozwalających na ocenę adekwatności modelu proporcjonalnego hazardu (Lee i Wang 200314)). Najszerzej stosowane są metody bazujące na resztach modelu. Podobnie jak inne graficzne metody oceny proporcjonalności hazardu jest to metoda subiektywna. Aby założenie proporcjonalnego hazardu było spełnione reszty względem czasu nie powinny układać się w żaden wzór ale powinny być losowo rozłożone w okolicach wartości 0.
Martingale - reszty te mogą być interpretowane jako różnica w czasie ![LaTeX $[0,t]$](/lib/exe/fetch.php?media=wiki:latex:/img990afe3dc2a01ee124e9c8ef79e63b21.png) pomiędzy obserwowaną licznością zdarzeń niepożądanych i przewidywaną przez model licznością tych zdarzeń. Wartość oczekiwana dla tych reszt to 0, ale ich wadą jest skośny rozkład utrudniający interpretację ich wykresu (zawierają się w przedziale od
pomiędzy obserwowaną licznością zdarzeń niepożądanych i przewidywaną przez model licznością tych zdarzeń. Wartość oczekiwana dla tych reszt to 0, ale ich wadą jest skośny rozkład utrudniający interpretację ich wykresu (zawierają się w przedziale od 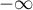 do 1).
do 1).
Deviance - podobnie jak Martingale asymptotycznie uzyskują wartość oczekiwaną równą 0, ale rozkładają się symetrycznie wokół zera z odchyleniem standardowym równym 1, gdy dopasowywany model jest odpowiedni. Wartość Deviance jest dodatnia, gdy obiekt badany przeżywa krócej niż oczekiwany na podstawie modelu czas, a ujemna gdy ten czas jest dłuższy. Analiza tych reszt jest wykorzystywana w badaniu proporcjonalności hazardu - ale jest to przede wszystkim narzędzie identyfikujące wartości odstające. W raporcie reszt, te z nich, które są oddalone o więcej niż 3 odchylenia standardowe od 0 oznaczone są kolorem czerwonym.
Schoenfeld - reszty te wyliczane są oddzielnie dla każdej zmiennej niezależnej i definiowane tylko dla obserwacji kompletnych. Dla każdej zmiennej niezależnej suma reszt Schoenfeld'a i ich wartość oczekiwana to 0. Zaletą przedstawiania reszt względem czasu dla każdej zmiennej jest możliwość zidentyfikowania zmiennej nie spełniającej w modelu założenia proporcjonalności hazardu. Jest to ta zmienna, której wykres reszt układa się w systematyczny wzór (najczęściej bada się tu liniową zależność reszt od czasu). Równomierne rozłożenie punktów względem wartości 0 świadczy o braku zależności reszt od czasu - czyli spełnieniu założenia proporcjonalności hazardu przez daną zmienną w modelu.
Gdy dla którejkolwiek zmiennej w modelu Cox'a nie jest spełnione założenie proporcjonalności hazardu, jednym z możliwych rozwiązań jest wykonanie analizy Cox'a oddzielnie dla każdego poziomu tej zmiennej.
Przykład c.d. (plik: remisjaBiałaczka.pqs)
2014/08/22 20:00
2014/08/22 20:00
Porównywanie modeli regresji PH Cox'a
Okno z ustawieniami opcji porównywania modeli wywołujemy poprzez menu Statystyka→Analiza przeżycia→Regresja PH Cox'a - porównywanie modeli
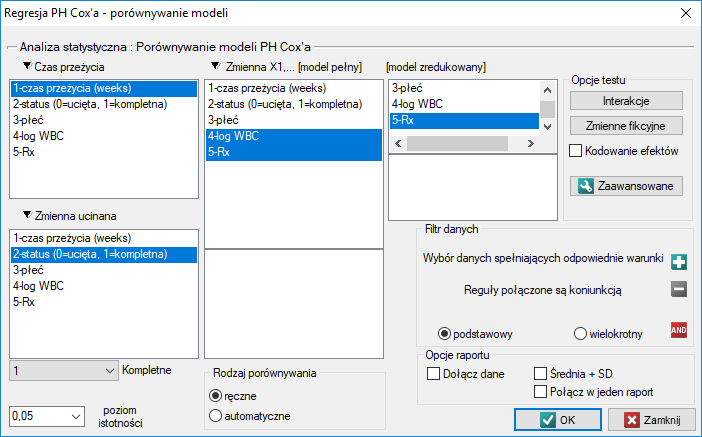
Ze względu na możliwość jednoczesnej analizy wielu zmiennych niezależnych w jednym modelu regresji Cox'a, istnieje problem wyboru optymalnego modelu. Wybierając zmienne niezależne należy pamiętać, by w modelu znajdowały się zmienne silnie związane z czasem przeżycia i słabo skorelowane między sobą.
Porównując modele z różną liczbą zmiennych niezależnych zwracamy uwagę na kryteria informacyjne (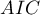 ,
, 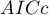 ,
, 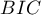 ) oraz współczynniki dopasowania modelu (
) oraz współczynniki dopasowania modelu (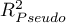 ,
, 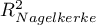 ,
, 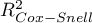 ). Modele porównywane są również przy użyciu testu ilorazu wiarygodności.
). Modele porównywane są również przy użyciu testu ilorazu wiarygodności.
Hipotezy:
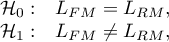
gdzie:
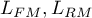 - maksimum funkcji wiarygodności w porównywanych modelach (pełnym i zredukowanym).
- maksimum funkcji wiarygodności w porównywanych modelach (pełnym i zredukowanym).
Statystyka testowa ma postać:
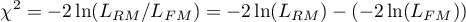
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 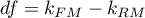 stopniami swobody, gdzie
stopniami swobody, gdzie 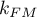 i
i 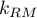 to ilość szacowanych parametrów w porównywanych modelach.
to ilość szacowanych parametrów w porównywanych modelach.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Decyzję o tym, który model wybrać podejmujemy na podstawie wielkości: 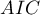 ,
, 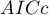 ,
, 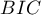 ,
, 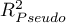 ,
, 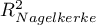 ,
, 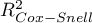 oraz wyniku testu ilorazu wiarygodności porównującego kolejno powstające (sąsiednie) modele. Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym
oraz wyniku testu ilorazu wiarygodności porównującego kolejno powstające (sąsiednie) modele. Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym  ) jest istotnie lepszy niż drugi.
) jest istotnie lepszy niż drugi.
W programie PQStat porównywanie modeli możemy przeprowadzić ręcznie lub automatycznie.
Ręczne porównywanie modeli - polega na zbudowaniu 2 modeli:
pełnego - modelu z większą liczbą zmiennych,
zredukowanego - modelu z mniejszą liczbą zmiennych  model taki powstaje z modelu pełnego po usunięciu zmiennych, które z punktu widzenia badanego zjawiska są zbędne.
model taki powstaje z modelu pełnego po usunięciu zmiennych, które z punktu widzenia badanego zjawiska są zbędne.
Wybór zmiennych niezależnych w porównywanych modelach a następnie wybór lepszego modelu, na podstawie uzyskanych wyników porównania, należy do badacza.
Automatyczne porównywanie modeli jest wykonywane w kilku krokach:
[krok 1] Zbudowanie modelu z wszystkich zmiennych.
[krok 2] Usunięcie jednej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.
[krok 3] Porównanie modelu pełnego i zredukowanego.
[krok 4] Usunięcie kolejnej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.
[krok 5] Porównanie modelu wcześniejszego i nowo zredukowanego.
[…]
W ten sposób powstaje wiele, coraz mniejszych modeli. Ostatni model zawiera tylko 1 zmienną niezależną.
Przykład (plik: remisjaBiałaczka.pqs)
Analiza opiera się na danych dotyczących białaczki opisanych w pracy Freireich i innych 196315) i analizowanych dalej przez wielu autorów min. Kleinbaum i Klein 200516)). Dane zawierają informację o czasie (w tygodniach) pozostawania w remisji aż do momentu wycofania pacjenta z badania z powodu wyjścia z remisji (nawrotu objawów) lub ucięcia informacji o pacjencie. Wyjście z remisji jest nastąpieniem zdarzenia niekorzystnego - traktowane jest jako obserwacja kompletna. Obserwacja jest ucięta jeśli pacjent pozostaje w badaniu do końca i remisja nie nastąpi lub jeśli opuści badanie.
Pacjenci przydzieleni zostali do dwóch grup: grupy leczonej tradycyjnie (oznaczonej jako 1 i czasami nazywanej „grupą placebo” ) i grupy leczonej nową metodą (oznaczonej jako 0). Zebrano informację o płci pacjentów (1=mężczyzna, 0=kobieta) oraz o wartościach wskaźnika określającego liczbę białych krwinek oznaczonego jako „log WBC”, który jest znanym czynnikiem prognostycznym.
Celem badania jest określenie wpływu sposobu leczenia na czas pozostawania w remisji przy uwzględnieniu możliwych czynników wikłających (confounder) i interakcji. W analizie uwagę skupimy na zmiennej „Rx (1=placebo, 0=new treatment)
”, zmienną „log WBC” umieścimy w modelu jako możliwy czynnik wikłający (modyfikujący uzyskany efekt). By ocenić ewentualny wpływ interakcji „Rx” i „log WBC” rozważymy także trzecią zmienną będącą iloczynem zmiennych wchodzących w skład interakcji. Zmienną tę dołączymy do modelu wybierając w oknie analizy przycisk Interakcje i dokonując odpowiednich ustawień.
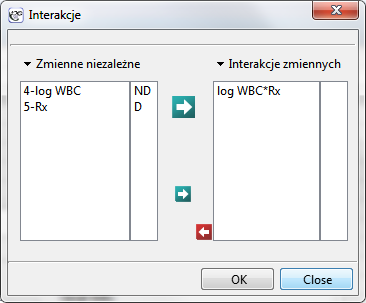
Budujemy trzy modele Coxa:
- [Model A] zawiera tylko zmienną „Rx”

- [Model B] zawiera zmienną „Rx” i potencjalną zmienną wikłającą „log WBC”

- [Model C] zawiera zmienną „Rx” zmienną „log WBC” oraz potencjalny efekt interakcji tych zmiennych: „Rx
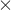 log WBC”
log WBC”

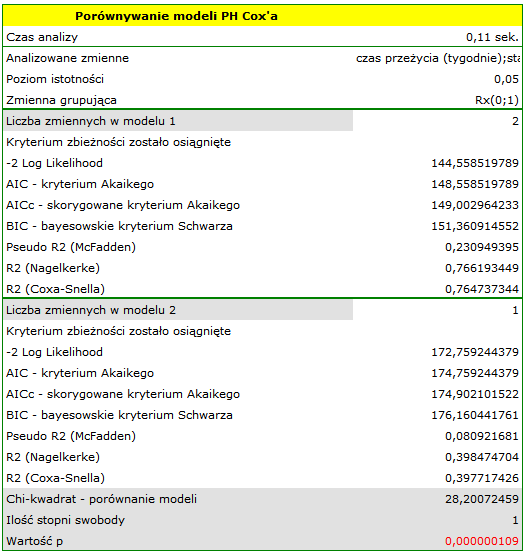
Zmienna mówiąca o interakcji „Rx” i „log WBC”, zawarta w modelu C jest w nim nieistotna (p=0.5103) według testu Walda. Możemy więc uznać za zbyteczne dalsze rozważanie w modelu interakcji tych dwóch zmiennych. Podobne wyniki uzyskamy porównując testem Ilorazu Wiarygodności model C z modelem B. Porównanie to możemy wykonać wybierając menu Regresja Cox'a - porównywanie modeli, uzyskamy wówczas wynik nieistotny (p=0.5134), co oznacza, że model C (model z interakcją) jest NIEistotnie lepszy niż model B (model bez interakcji).

Odrzucamy więc model C przechodząc do rozważania modelu B i modelu A.
HR dla „Rx” w modelu B wynosi 3.65, co oznacza, że hazard dla „grupy placebo” jest około 3.6 większy niż dla grupy pacjentów leczonych nową metodą. Model A zawiera tylko zmienną „Rx”, przez co nazywany jest zwykle modelem „surowym” (ang. crude model) ponieważ ignoruje efekt potencjalnych zmiennych wikłających. W modelu tym HR dla „Rx” wynosi 4.52 i jest sporo większe niż w modelu B. Przyjrzyjmy się jednak nie tylko punktowym wartościom estymatora HR ale również 95\% przedziałowi ufności dla tych estymatorów. Przedział dla „Rx” w modelu A ma szerokość 8.06 (10.09 minus 2.03) a w modelu B jest węższy: 6.74 (8.34 minus 1.60). Dlatego model B daje bardziej precyzyjną estymację HR niż model A. By ostatecznie zdecydować, który model (model A czy model B) będzie lepszy w oszacowaniu efektu leczenia („Rx”) ponownie wykonujemy analizę porównawczą modeli w module Regresja Cox'a - porównywanie modeli. Tym razem test Ilorazu Wiarygodności daje wynik istotny (p<0.0001), co ostatecznie potwierdza wyższość modelu B. Jest to model o najniższej wartości kryteriów informacyjnych (AIC=148.6, AICc=149 BIC=151.4) i wysokich wartościach dopasowania modelu (Pseudo 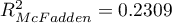 ,
, 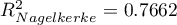 ,
, 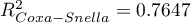 ).
).
Dopełnieniem powyższej analizy jest przedstawienie dla modelu B krzywych przeżycia (pozostawania w remisji) obu grup: leczonej nowym lekiem i tradycyjnie, skorygowanych o wpływ „log WBC”. Na wykresie obserwujemy różnice między grupami, występujące w poszczególnych punktach osi czasu. By wyrysować takie krzywe, po wybraniu opcji Dołącz wykres zaznaczamy opcję Funkcja przeżycia: w podgrupach … a nastęnie, by szybko zbudować wykres dwóch krzywych wybieram Szybkie podgrupy i wskazuję zmienną Rx. Opcja Zaawansowane podgrupy pozwala na zbudowanie dowolnej liczby dowolnie zdefiniowanych krzywych.

Na koniec ocenimy założenia regresjii Cox'a analizując reszty modelu względem czasu.
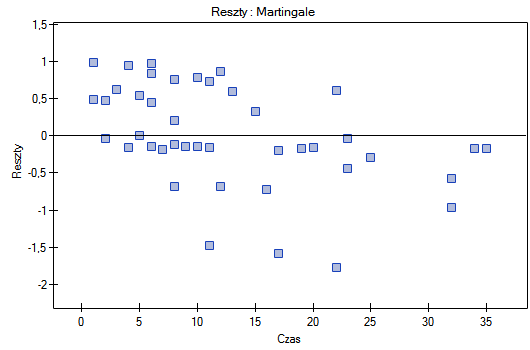
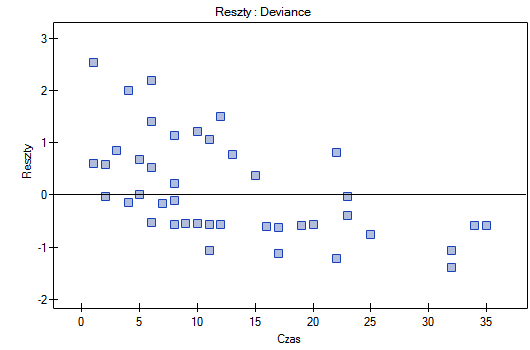
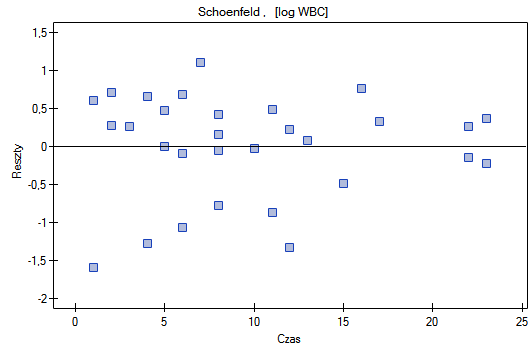

Nie obserwujemy odstających punktów, aczkolwiek reszty Martingale i Deviance są coraz niższe dla coraz dłuższego czasu. Natomiast reszty Schoenfeld'a przedstawiają symetryczny rozkład względem czasu. W przypadku reszt Schoenfeld'a analizę wykresu można wesprzeć różnego rodzaju testami mogącymi ocenić, czy punkty wykresu reszt układają się w pewien wzór np. zależność liniową. By tej analizy dokonać należy przekopiować reszty Schoenfeld'a oraz czas do arkusza danych i przetestować szukany rodzaj zależności. Wynik takiego testu dla każdej zmiennej wskazuje na spełnienie założenia proporcjonalności hazardu przez daną zmienną w modelu - gdy jest nieistotny statystycznie lub złamanie tego założenia - gdy jest istotny statystycznie. W rezultacie zmienną łamiącą założenia regresji proporcjonalnego hazardu Cox'a można wyłączyć z modelu. W przypadku zmiennych „Log WBC” i „Rx” symetryczny rozkład reszt sugeruje spełnienie założenia proporcjonalności hazardu przez te zmienne. Potwierdzeniem tego może być sprawdzenie zależności np. liniowej Pearsona, lub monotonicznej Spearmana dla tych reszt i czasu.
Dalej możemy dodać do modelu zmienną płeć. Musimy jednak postępować ostrożnie, gdyż na podstawie różnych źródeł wiadomo, że płeć może wpływać na funkcję przeżycia (pozostawania w remisji) dotyczącą białaczki w ten sposób, że funkcje przeżycia mogą układać się nieproporcjonalnie względem siebie wzdłuż osi czasu. Wykonujemy więc model Cox'a dla trzech zmiennych: zmiennej „Płeć”, „Rx” i „log WBC”. Zanim dokonamy interpretacji współczynników modelu sprawdzimy reszty Shoenfeld'a. Reszty przedstawiamy na wykresach, a wyniki reszt Shoenfeld'a oraz czasu przekopiujemy z raportu do nowego arkusza, gdzie sprawdzimy występowanie zależności monotonicznej Spearmana. W wyniku uzyskujemy wartość p=0.0259 (dla zależności czasu i reszt Shoenfeld'a dla płci), p=0.6192 (dla zależności czasu i reszt Shoenfeld'a dla log WBC) i p=0,1490 (dla zależności czasu i reszt Shoenfeld'a dla Rx) co potwierdza naruszenie założenia proporcjonalności hazardu przez zmienną płeć. Model Cox'a zbudujemy więc oddzielnie dla kobiet i mężczyzn. W tym celu analizę wykonamy dwukrotnie z włączonym filtrem danych. Za pierwszym razem filtr będzie wskazywał płeć żeńską (0), a za drugim razem płeć męską (1).
Dla kobiet

Dla mężczyzn

2014/08/22 20:00
1)
Kaplan E.L., Meier P. (1958), Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53:457-481
2)
Brookmeyer R. and Crowley J. (1982a), A confidence interval for the median survival time. Biometrics 38, 29-41
3)
Mantel N. and Haenszel W. (1959), Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22,719-748
4)
Mantel N. (1966), Evaluation of Survival Data and Two New Rank Order Statistics Arising in Its Consideration. Cancer Chemotherapy Reports, 50:163—170
5)
, 10)
Cox D.R. (1972), Regression models and life tables. Journal of the Royal Statistical Society, B34:187-220
6)
Gehan E. A. (1965a), A Generalized Wilcoxon Test for Comparing Arbitrarily Singly-Censored Samples. Biometrika, 52:203—223
7)
Gehan E. A. (1965b), A Generalized Two-Sample Wilcoxon Test for Doubly-Censored Data. Biometrika, 52:650—653
8)
Tarone R. E., Ware J. (1977), On distribution-free tests for equality of survival distributions. Biometrica, 64(1):156-160
9)
Armitage P., Berry G., (1994), Statistical Methods in Medical Research (3rd edition); Blackwell
11)
Breslow N.E. (1974), Covariance analysis of censored survival data. Biometrics, 30(1):89–99
12)
Peduzzi P., Concato J., Feinstein A.R., Holford T.R. (1995), Importance of events per independent variable in proportional hazards regression analysis. II. Accuracy and precision of regression estimates. Journal of Clinical Epidemiology, 48:1503-1510
13)
Volinsky C.T., Raftery A.E. (2000) , Bayesian information criterion for censored survival models. Biometrics, 56(1):256–262
14)
Lee E. T., Wang J. W. (2003), Statistical Methods for Survival Data Analysis, ed. third, Wiley
15)
Freireich E.O., Gehan E., Frei E., Schroeder L.R., Wolman I.J., et al. (1963), The effect of 6-mercaptopmine on the duration of steroid induced remission in acute leukemia. Blood, 21: 699–716
16)
Kleinbaum D. G., Klein M., (2005) Survival Analysis: A Self-Learning Text, Second Edition (Statistics for Biology and Health
statpqpl/survpl.txt · ostatnio zmienione: 2019/12/17 17:31 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

