Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:wielowympl:przygpl
Przygotowanie zmiennych do analizy
Dopasowanie grup
Dlaczego dokonuje się dopasowania grup?
Odpowiedzi na to pytanie jest bardzo wiele. Posłużymy się przykładem sytuacji medycznych.
Jeśli szacujemy efekt leczenia na podstawie eksperymentu z pełną randomizacją, to przypisując losowo osoby do grupy leczonej i nieleczonej tworzymy grupy podobne pod względem możliwych czynników zakłócających. Podobieństwo grup wynika z samego losowego przydziału. W takich badaniach możemy badać czysty (niezależny od czynników zakłócających) wpływ metody leczenia na wynik eksperymentu. W takim przypadku inne poza losowym dopasowanie grup nie jest konieczne.
Możliwość błędu pojawia się, gdy różnica w wyniku leczenia między leczonymi i nieleczonymi grupami może być spowodowana nie przez samo leczenie, ale przez czynnik, który skłonił do wzięcia udziału w leczeniu. Dzieje się tak wtedy, gdy z pewnych względów randomizacja nie jest możliwa, np. jest to badanie obserwacyjne lub ze względów etycznych nie możemy przypisać leczenia dowolnie. Wówczas sztuczne dopasowanie grup może mieć zastosowanie. Na przykład jeśli osoby które przydzielamy do grupy leczonej to osoby zdrowsze, a osoby które są w grupie kontrolnej to osoby o większym nasileniu choroby, wówczas to nie sam sposób leczenia, ale stan pacjenta przed leczeniem może mieć wpływ na wynik eksperymentu. Gdy zobaczymy taką nierównowagę grup, dobrze jest, kiedy możemy zdecydować się na randomizację, w ten sposób problem zostaje rozwiązany, gdyż losowanie osób do grup powoduje, że stają się one podobne. Można sobie jednak wyobrazić inną sytuację. Tym razem grupą, którą jesteśmy zainteresowani nie będą osoby poddane leczeniu lecz osoby palące, a grupą kontrolną osoby niepalące, a analizy będą miały na celu wykazanie niekorzystnego wpływu palenia na występowanie raka płuc. Wówczas, chcąc sprawdzić czy palenie rzeczywiście wpływa na zwiększenie ryzyka zachorowania, byłoby nieetycznym wykonanie badania z pełną randomizacją, ponieważ oznaczałoby ono, że losowo wybrane do grupy ryzyka osoby zmusimy do palenia. Rozwiązaniem tej sytuacji jest ustalenie grupy narażonej, czyli wylosowanie pewnej liczby osób spośród osób które już palą, a następnie dobór grupy kontrolnej złożonej z niepalących. Grupa kontrolna powinna być dobrana, ponieważ zostawiając dobór przypadkowi możemy uzyskać grupę niepalącą, która jest młodsza od palących tylko ze względu na fakt, że w naszym kraju palenie staje się mniej modne, a więc automatycznie wśród osób niepalących jest wiele osób młodych. Kontrolna powinna być wylosowana z osób niepalących, ale tak, by była jak najbardziej podobna do grupy leczonej. W ten sposób przybliżamy się do badania czystego (niezależnego od wybranych czynników zakłócających takich jak chociażby wiek) wpływu palenia/nie palenia na wynik eksperymentu czyli w tym przypadku wystąpienie nowotworu płuc. Taki dobór możemy wykonać właśnie poprzez zaproponowane w programie dopasowanie.
Jedną z głównych zalet kontrolowanego przez badacza dopasowania jest upodobnienie się grupy kontrolnej do grupy leczonej, ale jest to też największa wada tej metody. Jest to zaleta, ponieważ nasze badanie coraz bardziej przypomina badanie randomizowane. W badaniu randomizowanym grupa bada i kontrolna jest podobna pod względem niemalże wszystkich cech, również tych których nie badamy – losowy podział zapewnia nam to podobieństwo. W wyniku zastosowania dopasowania kontrolowanego przez badacza grupa leczona i kontrolna stają się podobne pod względem tylko wybranych cech.
Sposoby oceny podobieństwa:
Dwa pierwsze wymienione sposoby opierają się na dopasowaniu grup poprzez dopasowanie wyników skłonności (ang. Propensity Score Matching, PSM). Ten rodzaj dopasowania został zaproponowany przez Rosenbauma i Rubina 1). W praktyce jest to technika doboru grupy kontrolnej (osób nie leczonych lub leczonych minimalnie/standardowo) do grupy leczonej na podstawie prawdopodobieństwa opisującego skłonność badanych do przypisania leczenia w zależności od obserwowanych zmiennych towarzyszących. Wynik prawdopodobieństwa opisującego skłonności, z angielskiego nazywany Propensity Score jest wynikiem równoważącym, dlatego w wyniku doboru grupy kontrolnej do grupy leczonej rozkład zmierzonych zmiennych towarzyszących staje się bardziej podobny między osobami leczonymi i nieleczonymi. Trzecia metoda nie wyznacza prawdopodobieństwa dla każdej osoby, ale wyznacza macierz odległości/niepodobieństwa, która wskazuje obiekty najbliższe/najbardziej podobne pod względem wielu wybranych cech.
Metody:
- Zadane prawdopodobieństwo – czyli podaną dla każdej badanej osoby wartość z przedziału od 0 do 1, określającą prawdopodobieństwo przynależenia do grupy leczonej czyli Propensity Score. Takie prawdopodobieństwo może zostać wyznaczone wcześniej różnymi metodami. Na przykład w modelu regresji logistycznej, poprzez sieci neuronowe lub wiele innych metod. Jeśli osoba z grupy, z której losujemy kontrole uzyska Propensity Score podobne do tego jaki uzyskała osoba z grupy leczonej, wówczas może ona wejść do analizy, ponieważ obie te osoby są podobne pod względem cech, jakie były rozważane przy wyznaczaniu Propensity Score.
- Wyznaczone z modelu regresji logistycznej – ponieważ regresja logistyczna to najczęściej stosowana metoda doboru, program PQStat daje możliwość wyznaczenia automatycznie w oknie analizy wartości Propensity Score w oparciu o tę metodę. Dopasowanie przebiega dalej przy wykorzystaniu uzyskanego w ten sposób Propensity Score.
- Macierz podobieństwa/odległości – na podstawie tej opcji nie jest wyznaczana wartość Propensity Score, ale budowana jest macierz wskazująca odległość każdej osoby z grupy leczonej do osoby z grupy kontrolnej. Użytkownik może zadać warunki brzegowe np. może wskazać, że osoba dobrana do danej osoby z grupy badanej nie może się od niej różnic wiekiem bardziej niż o 3 lata i musi być tej samej płci. Odległości w budowanej macierzy wyznaczone są w oparciu o dowolną metrykę lub sposób opisujący niepodobieństwo. Ten sposób doboru grupy kontrolnej do leczonej jest bardzo elastyczny. Oprócz dowolnego wyboru sposobu wyznaczania odległości/niepodobieństwa, w wielu metrykach pozwala na wskazywanie wag określających to, jak ważne są dla badacza poszczególne zmienne, tzn. na podobieństwie jednych zmiennych może badaczowi zależeć bardziej, podczas gdy podobieństwo innych jest mniej ważne. Jednak w przypadku wyboru macierzy odległości/niepodobieństwa zalecana jest duża ostrożność. Wiele cech i wiele soposobów wyznaczania odległości wymaga wcześniejszego standaryzowania lub normalizowania danych, ponadto wybór odwrotności odległości lub podobieństwa (zamiast niepodobieństwa) może skutkować wyszukiwaniem najbardziej odległych i niepodobnych obiektów, podczas gdy standardowo stosujemy te metody do wyszukiwania obiektów podobnych. Jeśli badacz nie ma określonych powodów zmiany metryki, standardowo zalecane jest korzystanie z odległości statystycznej czyli metryki
Mahalanobisa– jest ona najbardziej uniwersalna, nie wymaga wcześniejszej standaryzacji danych i jest odporna na skorelowanie zmiennych. Dokładniejszy opis dostępnych w programie odległości i miar niepodobieństwa/podobieństwa oraz sposób ineterpretacji uzyskanych wyników można znaleźć w dziale Macierz podobieństwa.
W praktyce istnieje wiele metod wskazujących jak blisko znajdują się porównywane obiekty, w tym przypadku osoby leczone i nieleczone. W programie zaproponowane są dwie:
- Metoda najbliższego sąsiada – jest standardowym sposobem doboru obiektów nie tylko takich o podobnym Propensity Score, ale również takich których odległość/niepodobieństwo znajdujące się w macierzy jest najmniejsze.
- Metoda najbliższego sąsiada, bliższego niż… - działa w ten sam sposób, co metoda najbliższego sąsiada z tą różnicą, że dopasowane mogą zostać jedynie obiekty znajdujące się odpowiednio blisko. Granicę tej bliskości wyznaczamy podając wielkość opisującą próg, za którym znajdują się już obiekty tak niepodobne do badanych, że nie chcemy dać im szansy na dołączenie do nowo budowanej grupy kontrolnej. W przypadku gdy analiza opiera się na Propensity Score lub na macierzy określanej przez niepodobieństwo, najbardziej niepodobne obiekty to te odległe o 1, a najbardziej podobne, to te odległe o 0. Wybierając więc tę metodą należy podać wartość bliższą 0, gdy dobieramy bardziej restrykcyjnie, lub bliższą 1, gdy próg ten będzie umieszczony dalej. Gdy zamiast niepodobieństwa w macierzy wyznaczamy odległości, wówczas wielkość minimalna to wiąż 0, ale wielkość maksymalna nie jest z góry określona.
Dopasować możemy bez zwracania obiektów już wylosowanych lub ze zwracaniem tych obiektów ponownie do grupy, z której losujemy.
- Dopasowanie bez zwracania – w przypadku stosowania dopasowywania bez zwracania, gdy nieleczona osoba został wybrana do dopasowania do danej leczonej osoby, ta nieleczona osoba nie jest już dostępna do rozważenia jako potencjalne dopasowanie dla kolejnych osób leczonych. W rezultacie każda nieleczona osoba jest zawarta w co najwyżej jednym dopasowanym zestawie.
- Dopasowanie ze zwracaniem – dopasowanie ze zwracaniem pozwala na uwzględnienie danej nieleczonej osoby więcej niż raz w jednym dopasowanym zestawie. Kiedy stosuje się dopasowanie ze zwracaniem, dalsze analizy, a w szczególności oszacowanie wariancji musi uwzględniać fakt, że ta sama nieleczona osoba może znajdować się w wielu dopasowanych zestawach.
W przypadku gdy, nie da się jednoznacznie dobrać osoby nieleczonej do leczonej, ze względu na to, że w grupie z której wybieramy mamy więcej osób tak samo dobrze pasujących do osoby leczonej, wówczas połączona zostaje jedna z tych osób wybrana w sposób losowy. Dla wznowionej analizy domyślnie ustawiony jest stały seed, więc wyniki powtórzonego losowania będą te same, jednak gdy analizę wykonamy na nowo seed zostaje zmieniony i wynik losowania może być inny.
W przypadku gdy, nie da się dobrać osoby nieleczonej do leczonej, ze względu na to, że w grupie z której wybieramy nie ma już osób do dołączenia np. osoby pasujące zostały już dołączone do innych osób leczonych lub zbiór, z którego wybieramy nie ma osób podobnych, wówczas osoba ta pozostaje bez pary.
Najczęściej dokonuje się dopasowania 1:1, tzn. dla jednej osoby leczonej dobiera się jedną osobę nie leczoną. Jednak, jeśli oryginalna grupa kontrolna, z której dokonujemy losowania jest wystarczająco duża i potrzebujemy wylosować więcej osób, to można wybrać dopasowanie 1:k, gdzie k wskazuje liczbę osób, która powinna zostać dopasowana do każdej osoby leczonej.
Ocena dopasowania
Po dopasowaniu grupy kontrolnej do grupy leczonej wyniki takiego dopasowania możemy zwrócić do arkusza tzn. uzyskać nową grupę kontrolną. Nie należy jednak zakładać, że stosując dopasowanie zawsze uzyskamy satysfakcjonujące wyniki. W wielu sytuacjach grupa, z której losujemy nie posiada wystarczającej liczby takich obiektów, które są wystarczająco podobne do grupy leczonej. Dlatego zawsze wykonane dopasowanie należy ocenić. Istnieje wiele metod oceny dopasowania grup. W programie wykorzystano metody opierające się na standaryzowanej różnicy grup, szerzej opisywane m.in. w pracach P.C Austina 2)3). Takie podejście pozwala na porównanie względnej równowagi zmiennych mierzonych w różnych jednostkach, a na jego wynik nie ma wpływu wielkość próby. Zrezygnowano z oszacowania zgodności przy pomocy testów statystycznych, gdyż dobrana grupa kontrolna jest zwykle dużo mniejsza niż oryginalna grupa kontrolna, przez co uzyskiwane wartości p testów porównujących grupę badaną do mniejszej grupy kontrolnej częściej zostają z założeniem hipotezy zerowej, a więc nie wykazują istotnych różnic ze względu na zmniejszoną liczność.
Dla porównania zmiennych ciągłych wyznaczamy standaryzowaną różnicę średnich:

gdzie:
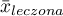 ,
, 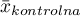 - to średnia wartość zmiennej w grupie leczonej i średnia wartość zmiennej w grupie kontrolnej,
- to średnia wartość zmiennej w grupie leczonej i średnia wartość zmiennej w grupie kontrolnej,
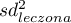 ,
, 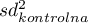 - to wariancja w grupie leczonej i wariancja w grupie kontrolnej.
- to wariancja w grupie leczonej i wariancja w grupie kontrolnej.
Dla porównania zmiennych binarnych (o dwóch kategoriach, zwykle 0 i 1) wyznaczamy standaryzowaną różnicę częstości:
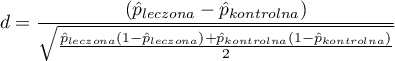
gdzie:
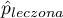 ,
, 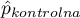 - to częstość wartości opisanej jako 1 w grupie leczonej i częstość wartości opisanej jako 1 w grupie kontrolnej.
- to częstość wartości opisanej jako 1 w grupie leczonej i częstość wartości opisanej jako 1 w grupie kontrolnej.
Zmienne o wielu kategoriach powinniśmy rozbić w analizie regresji logistycznej na zmienne fikcyjne o dwóch kategoriach i sprawdzając dopasowania obu grup wyznaczać dla nich standaryzowaną różnicę częstości.
Uwaga!
Chociaż nie ma powszechnie uzgodnionego kryterium określającego, jaki próg znormalizowanej różnicy można zastosować do wskazania istotnej nierównowagi, wskazówką może być standaryzowana różnica mniejsza niż 0.1 (zarówno w ocenie średnich jak i częstości)4). Dlatego, by uznać, że grupy są dobrze dobrane powinniśmy obserwować standaryzowane różnice położone blisko wartości 0, a najlepiej, by nie wychodziły poza przedział od -0.1 do 0.1. Graficznie wyniki te przedstawiamy na wykresie punktowym. Ujemne różnice świadczą o niższych średnich/częstościach w grupie leczonej, dodatnie w grupie kontrolnej.
Uwaga!
Uzyskane w raportach dopasowanie 1:1 oznacza podsumowanie dotyczące grupy badanej i odpowiadającej jej grupy kontrolnej uzyskanej w pierwszym dopasowaniu, dopasowanie 1:2 oznacza podsumowanie dotyczące grupy badanej i odpowiadającej jej grupy kontrolnej uzyskanej w pierwszym + drugim dopasowaniu (czyli nie dotyczy grupy badanej i odpowiadającej jej grupy kontrolnej uzyskanej tylko w drugim dopasowaniu), itd. –
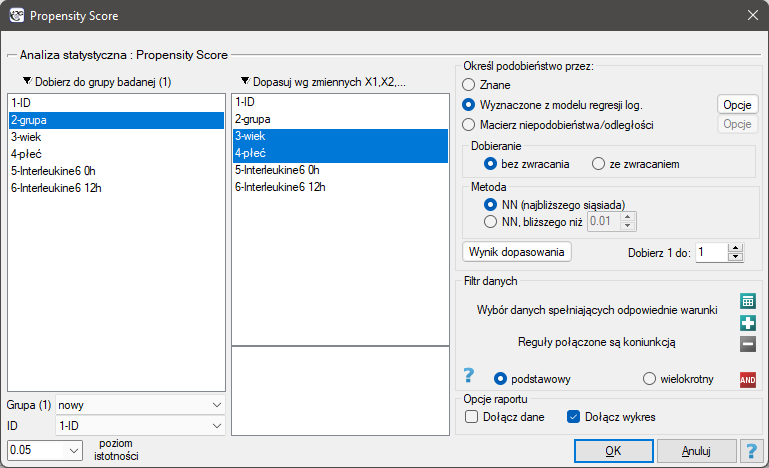
Okno z ustawieniami opcji dopasowania grup wywołujemy poprzez menu Statystyki zaawansowane→Modele wielowymiarowe→Dopasowanie grup
Przykład (plik dopasowanie.pqs)
Chcemy porównać dwa sposoby leczenia pacjentów po wypadkach, sposób tradycyjny i nowy sposób leczenia. Poprawne działanie obu sposobów leczenia powinno być obserwowane w obniżającym się poziomie wybranych cytokin. By porównać skuteczność tych dwóch sposobów leczenia obydwa one powinny zostać przeprowadzone na pacjentach, którzy są dość podobni. Wtedy będziemy mieli pewność, że ewentualne różnice w skuteczności tych metod będą wynikały z samego oddziaływania leczenia a nie z innych różnic między pacjentami przydzielonymi do różnych grup. Badanie jest przeprowadzone a posteriori, to znaczy bazuje na danych zebranych od pacjentów z historii leczenia. Dlatego badacze nie mieli wpływu na przypisanie pacjentów do grupy leczonej nowym lekiem i grupy leczonej tradycyjnie. Zauważono, że tradycyjny sposób leczenia był przepisywany głównie pacjentom starszym, podczas, gdy nowy sposób leczenia pacjentom w młodszym wieku, u których łatwiej jest obniżać poziom cytokin. Grupy były dość podobne co do struktury płci, ale nie identyczne.
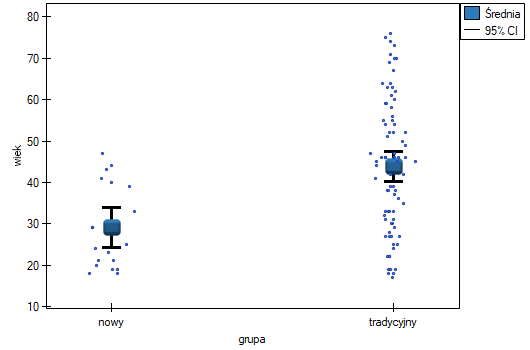
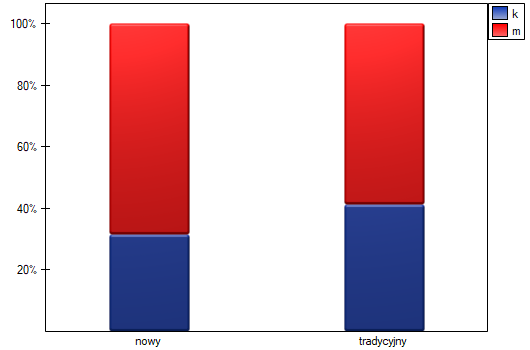
Gdyby przeprowadzono planowane badanie na tak wybranych grupach pacjentów, to nowy sposób miałby łatwiejsze zadanie do wykonania, gdyż młodsze organizmy lepiej mogłyby reagować na leczenie. Warunki eksperymentu nie byłyby równe dla obydwu sposobów, co mogłoby zafałszować wyniki analiz i wyciągane wnioski. Dlatego zdecydowano się dobrać grupę leczoną tradycyjnie tak, by była podobna do grupy badanej leczonej nowym sposobem. Dopasowania planujemy dokonać względem dwóch cech tzn. względem wieku i płci. Grupa leczona tradycyjnie jest większa (80 osób) od grupy leczonej nowym lekiem (19 osób), dlatego jest duża szansa na to, że uda się dobrać grupy tak, by były podobne. Losowego doboru dokonujemy poprzez algorytm modelu regresji logistycznej zaszyty w PSM. Pamiętamy, by płeć była zakodowana liczbowo, gdyż w analizie regresji logistycznej biorą udział jedynie wartości liczbowe. Jako metodę wybieramy najbliższe sąsiedztwo. Chcemy by ta sama osoba nie mogła zostać wybrana dwukrotnie, więc wybieramy losowanie bez zwracania. Spróbujemy dopasowania 1:1, czyli dla każdej osoby leczonej nowym lekiem dopasujemy jedną osobę leczoną tradycyjnie. Pamiętajmy przy tym, że dobór jest losowy, a więc zależy od losowej wartości seed ustawionej przez nasz komputer więc losowanie przeprowadzone przez czytelnika może się różnic od wartości przedstawionych tutaj.
Podsumowanie doboru obejrzymy w tabelach i na wykresach.
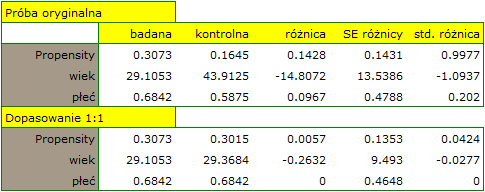
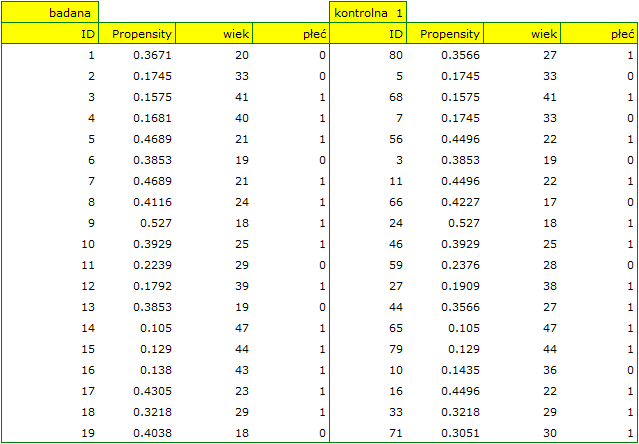
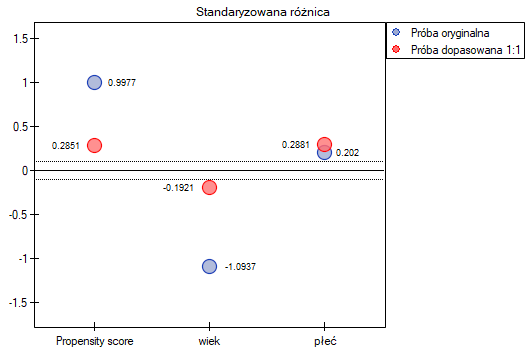
W próbie oryginalnej średnia wieku jest o ponad 14 lat wyższa u pacjentów leczonych tradycyjnie (różnica między średnimi wynosi 14.8072), natomiast struktura płci różni się o niecałe 10% (0.0967). Znacznie mniejsze różnice obserwujemy pomiędzy pacjentami leczonymi nowym sopsobem i dopasowanymi do nich osobami leczonymi tradycyjnie. Najwięcej informacji o jakości dopasowania uzyskamy na podstawie różnic standaryzowanych (ostatnia kolumna tabeli i wykres).
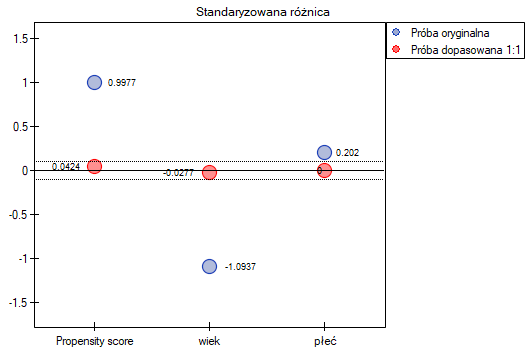
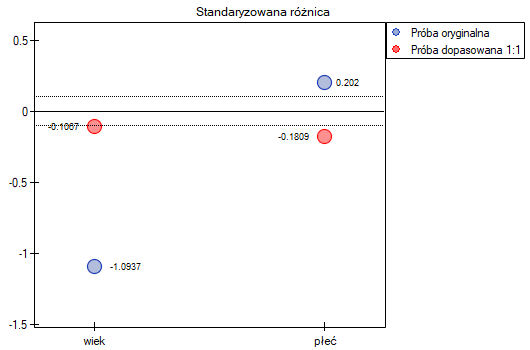
Linia na poziomie 0 oznacza równowagę grup (różnicę między grupami równą 0). Gdy grupy znajdują się w równowadze co do zadanych cech, wówczas wszystkie punkty na wykresie znajdują się blisko tej linii tzn. w okolicach przedziału od -0.1 do 0.1. W przypadku próby oryginalnej (kolor niebieski) widzimy znaczne oddalenie Propensity Score. Jak wiemy, ten brak dopasowania jest skutkiem głównie niedopasowania wieku – jego standaryzowana różnica znajduje się w dużej odległości od 0, a w mniejszym stopniu niedopasowania płci.
Dokonując dopasowania uzyskaliśmy grupy bardziej podobne do siebie (kolor czerwony na wykresie). Standaryzowana różnica między grupami określona przez Propensity Score wynosi 0.0424, czyli mieści sie w wyznaczonym przedziale. Wiek obu grup jest już podobny – grupa leczona tradycyjnie różni się od grupy leczonej nowym sposobem średnio o niecały rok (różnica między średnimi przedstawiona w tabeli to 0.2632) a standaryzowana różnica między średnimi wynosi -0.0277. W przypadku płci dopasowanie jest idealne, tzn. odsetek kobiet i mężczyzn jest taki sam w obu grupach (standaryzowana różnica odsetków przedstawiona w tabeli i na wykresie wynosi teraz 0). Tak przygotowane dane możemy zwrócić do arkusza i poddać planowanym przez siebie analizom.
Przyglądając się uzyskanemu przed chwilą podsumowaniu można zauważyć, że mimo dobrego zbalansowania grup i dobrania wielu osób idealnie, znajdują się pojedyncze osoby, które nie są do siebie tak podobne jak moglibyśmy oczekiwać.
Czasami oprócz uzyskania grup dobrze zbalansowanych badaczom zależy na dokładnym określeniu sposobu doboru poszczególnych osób, tzn. uzyskaniu większego wpływu na podobieństwo obiektów co do wartości Propensity Score lub na podobieństwo obiektów co do wartości konkretnych cech. Wówczas, jeśli grupa z której losujemy jest wystarczająco liczna, analiza może przynieść korzystniejsze z punktu widzenia badacza efekty, ale gdy w grupie z której losujemy zabraknie obiektów spełniających nasze kryteria, wówczas dla części osób nie uda się znaleźć dopasowania spełniającego nasze warunki.
- Załóżmy, że chcielibyśmy uzyskać takie grupy, których Propensity Score (tzn. skłonność do wzięcia udziału w badaniu) różni się nie więcej niż …
Jak ustalić tę wartość? Można zerknąć na raport z wcześniejszej analizy, gdzie podana jest najmniejsza i największa odległość między losowanymi obiektami.

W naszym przypadku obiekty najbliższe sobie różnią się o min=0, a najdalsze o max=0.5183. Spróbujemy więc sprawdzić jaki dobór uzyskamy gdy będziemy dopasowywać do osób leczonych nową metodą takie osoby leczone tradycyjnie, których Propensity Score będzie bardzo bliskie np. mniejsze od 0.01.
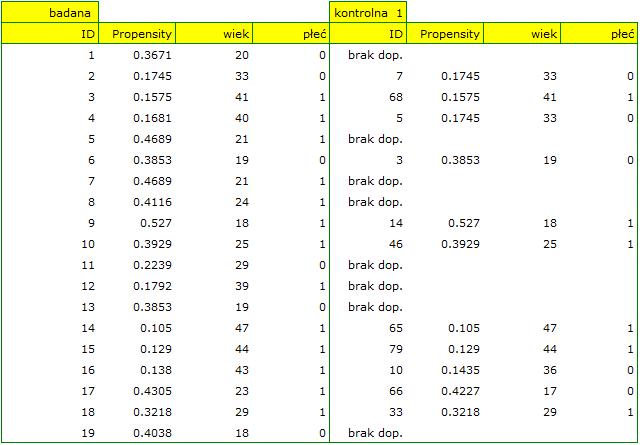
Widzimy, że tym razem z nie udało się dobrać całej grupy. Porównując Propensity Score dla poszczególnych par (leczonych nowym lekiem i leczonych tradycyjnie) widzimy, że różnice są naprawdę niewielkie. Jednak ze względu na to, że dobrana grupa jest znacznie mniejsza, to podsumowując cały proces doboru musimy zauważyć że zarówno Propensity Score, wiek jak i płeć nie znalazły się wystarczająco blisko linii na poziomie 0. Nasza chęć poprawy sytuacji nie doprowadziła do pożądanego skutku, a uzyskane grupy nie są wystarczająco dobrze zbalansowane.
- Załóżmy, że chcielibyśmy uzyskać takie pary (osób leczonych nową metodą i osób leczonych tradycyjnie), które są tej samej płci i których wiek nie różni się więcej niż 3 lata. W losowaniu opartym o Propensity Score nie mieliśmy tego typu możliwości wpływania na zakres zgodności każdej ze zmiennych. Do tego celu skorzystamy z innej metody, nie opartej na Propensity Score, ale bazującej na macierzach odległości/niepodobieństwa. Po wybraniu przycisku
Opcjewybieramy zaproponowaną macierz odległości statystycznej Mahalanobisa i ustawiamy dopasowanie sąsiedztwa na maksymalną odległość równą 3 dla wieku i równą 0 dla płci. W efekcie dla dwóch osób nie udało się znaleźć dopasowania, ale pozostałe dopasowania spełniają zadane kryteria.
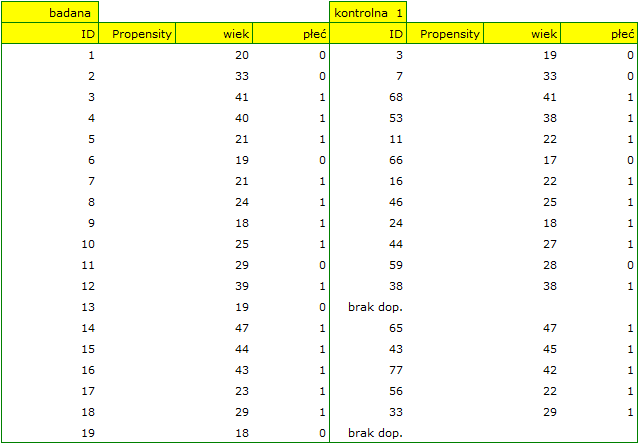
Podsumowując całościowo przeprowadzone losowanie musimy zauważyć, że mimo, że spełnia ono nasze założenia, to uzyskane grupy nie są tak dobrze zbalansowane jak to było w naszym pierwszym losowaniu przeprowadzonym w oparciu o Propensity Score. Punkty oznaczone kolorem czerwonym, przedstawiające jakość dopasowania pod względem wieku i jakość dopasowania pod względem płci odbiegają nieco od linii identyczności ustalonej na poziomie 0, co oznacza że średnia różnica wieku i struktury płci jest obecnie większa niż w pierwszym dopsowaniu.
To od badacza zależy, który sposób przygotowania danych będzie dla niego bardziej korzystny.
Ostatecznie, gdy decyzja zostanie podjęta, dane można zwrócić do nowego arkusza. By tego dokonać wracamy do wybranego przez siebie raportu i w drzewe projektu pod prawym przyciskiem wybieramy menu Powtórz analizę. W oknie tej samej analizy wskazujemy przycisk Wynik dopasowania i określamy, które jeszcze zmienne będą zwrócone do nowego arkusza.
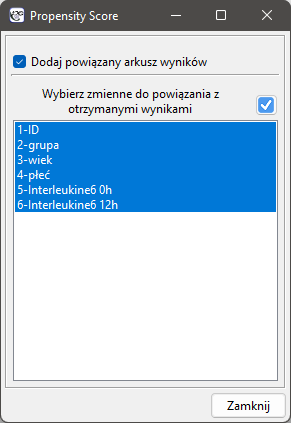
W efekcie otrzymamy nowy arkusz danych, w którym obok siebie znajdą się dane dotyczące osób leczonych nowym sposobem oraz dopasowanych do nich osób leczonych tradycyjnie.
2022/02/26 15:04
· admin
Interakcje
Interakcje rozważane są w modelach wielowymiarowych a ich występowanie oznacza, że wpływ zmiennej niezależnej ( ) na zmienną zależną (
) na zmienną zależną ( ) jest inny, w zależności od poziomu kolejnej zmiennej niezależnej (
) jest inny, w zależności od poziomu kolejnej zmiennej niezależnej ( ) lub szeregu kolejnych zmiennych niezależnych. By można było rozważać interekcje w modelach wielowymiarowych należy wskazać zmienne mówiące o prawdopodobnych interakcjach, czyli iloczyny odpowiednich zmiennych. W tym celu wybieramy przycisk
) lub szeregu kolejnych zmiennych niezależnych. By można było rozważać interekcje w modelach wielowymiarowych należy wskazać zmienne mówiące o prawdopodobnych interakcjach, czyli iloczyny odpowiednich zmiennych. W tym celu wybieramy przycisk Interakcje w oknie wybranej analizy wielowymiarowej. W oknie ustawiania interakcji z wciśniętym przyciskiem CTRL wskazujemy zmienne, które mają tworzyć interakcje i przenosimy je do sąsiedniej listy przy pomocy strzałki. Uruchamiając przycisk OK uzyskujemy odpowiednie kolumny w arkuszu danych.
W analizie interakcji wybór odpowiedniego kodowania zmiennych dychotomicznych pozwala na uniknięcie przeparametryzowania związanego z interakcjami. Przeparametryzowanie powoduje, że efekty niższego rzędu dla zmiennych dychotomicznych są redundantne względem uwikłanych interakcji wyższego rzędu. W rezultacie uwzględnienie w modelu interakcji wyższego rzędu niweluje efekt interakcji rzędów niższych, nie pozwalając na ich prawidłową ocenę. By uniknąć przeparametryzowania w modelu w którym występują interakcje zmiennych dychotomicznych zaleca się wybierać opcję kodowanie efektów.
W modelach z interakcjami należy pamiętać o odpowiednim ich „przycinaniu”, tak by usuwając efekty główne usunąć również efekty rzędów wyższych, które są od nich zależne. To znaczy: jeśli w modelu mamy następujące zmienne (efekty główne):  ,
,  ,
, 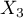 i interakcje:
i interakcje:  ,
,  ,
,  ,
, 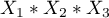 , to usuwając z modelu zmienną
, to usuwając z modelu zmienną  musimy usunąć również te interakcje, w których ona występuje, czyli:
musimy usunąć również te interakcje, w których ona występuje, czyli:  ,
,  oraz
oraz 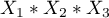 .
.
2014/08/22 20:00
Kodowanie zmiennych
Problemem w przygotowaniu danych do analizy wielowymiarowej jest odpowiednie zakodowanie zmiennych nominalnych i porządkowych. Jest to ważny element przygotowania danych do analizy, gdyż ma zasadniczy wpływ na interpretację współczynników modelu. Zmienne nominalne lub porządkowe dzielą analizowane obiekty na dwie lub więcej kategorii, przy czym zmienne dychotomiczne (o dwóch kategoriach, 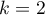 ) wystarczy tylko odpowiednio zakodować, a zmienne o wielu kategoriach (
) wystarczy tylko odpowiednio zakodować, a zmienne o wielu kategoriach (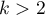 ) rozbić na zmienne fikcyjne (ang. dummy variable) o dwóch kategoriach oraz zakodować.
) rozbić na zmienne fikcyjne (ang. dummy variable) o dwóch kategoriach oraz zakodować.
- [
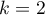 ] Jeśli zmienna jest dychotomiczna, badacz sam decyduje o sposobie, w jaki wprowadzi dane ją reprezentujące, może więc wprowadzić dowolne kody liczbowe np. 0 i 1. W programie można zmienić własne kodowanie na
] Jeśli zmienna jest dychotomiczna, badacz sam decyduje o sposobie, w jaki wprowadzi dane ją reprezentujące, może więc wprowadzić dowolne kody liczbowe np. 0 i 1. W programie można zmienić własne kodowanie na kodowanie efektuzaznaczając tę opcję w oknie wybranej analizy wielowymiarowej. Kodowanie takie powoduje zastąpienie mniejszej wartości wartością -1 a wartości większej wartością 1. - [
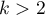 ] Jeśli zmienna ma wiele kategorii, to w oknie wybranej analizy wielowymiarowej wybieramy przycisk
] Jeśli zmienna ma wiele kategorii, to w oknie wybranej analizy wielowymiarowej wybieramy przycisk Zmienne fikcyjnei ustawiamy kategorię referencyjną/bazową dla tych zmiennych, które chcemy rozbić na zmienne fikcyjne. Zmienne te będą zakodowane zero-jedynkowo, chyba, że w oknie analizy zostanie wybrana opcjakodowanie efektu- wówczas kodowane będą jako -1, 0 i 1.
Kodowanie zero-jedynkowe (dummy coding) jest wykorzystywane by przy pomocy modeli wielowymiarowych odpowiedzieć na pytanie: Jak wyniki ( ), w każdej analizowanej kategorii, różnią się od wyników kategorii referencyjnej. Kodowanie to polega na przypisaniu wartości 0 lub 1 do każdej kategorii danej zmiennej. Kategoria zakodowana jako 0 jest wówczas kategorią referencyjną (reference).
), w każdej analizowanej kategorii, różnią się od wyników kategorii referencyjnej. Kodowanie to polega na przypisaniu wartości 0 lub 1 do każdej kategorii danej zmiennej. Kategoria zakodowana jako 0 jest wówczas kategorią referencyjną (reference).
- [
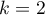 ] Gdy kodowana zmienna jest dychotomiczna, wówczas umieszczając ją w modelu regresji uzyskamy wyliczony dla niej współczynnik (
] Gdy kodowana zmienna jest dychotomiczna, wówczas umieszczając ją w modelu regresji uzyskamy wyliczony dla niej współczynnik (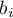 ). Współczynnik ten jest odniesieniem wartości zmiennej zależnej
). Współczynnik ten jest odniesieniem wartości zmiennej zależnej  dla kategorii 1 do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu).
dla kategorii 1 do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu). - [
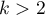 ] Gdy analizowana zmienna ma więcej niż dwie kategorie, wówczas
] Gdy analizowana zmienna ma więcej niż dwie kategorie, wówczas  kategorii jest reprezentowanych przez
kategorii jest reprezentowanych przez 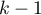 zmiennych fikcyjnych (dummy variables) o kodowaniu zero-jedynkowym. Tworząc zmienne o kodowaniu zero-jedynkowym wybiera się kategorię, dla której nie tworzy się zmiennej fikcyjnej. Kategoria ta traktowana jest w modelach jako kategoria odniesienia (gdyż w każdej zmiennej zakodowanej w sposób zero-jedynkowy odpowiadają jej wartości 0).
zmiennych fikcyjnych (dummy variables) o kodowaniu zero-jedynkowym. Tworząc zmienne o kodowaniu zero-jedynkowym wybiera się kategorię, dla której nie tworzy się zmiennej fikcyjnej. Kategoria ta traktowana jest w modelach jako kategoria odniesienia (gdyż w każdej zmiennej zakodowanej w sposób zero-jedynkowy odpowiadają jej wartości 0).
Gdy tak uzyskane zmienne 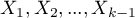 o kodowaniu zero-jedynkowym zostaną umieszczone w modelu regresji, wówczas zostaną dla nich wyliczone współczynniki
o kodowaniu zero-jedynkowym zostaną umieszczone w modelu regresji, wówczas zostaną dla nich wyliczone współczynniki  .
.
- [
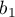 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w  ) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu);
) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu); - [
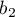 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w  ) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu)
) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu) - […]
- [
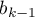 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w 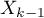 ) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu);
) do kategorii referencyjnej (w korekcji o pozostałe zmienne w modelu);
Przykład
Zakodujemy zgodnie z kodowaniem zero-jedynkowym zmienną płeć o dwóch kategoriach (płeć męską wybierzemy jako kategorię referencyjną) i zmienną wykształcenie o 4 kategoriach (wykształcenie podstawowe wybierzemy jako referencyjne).
![LaTeX \begin{tabular}{|c|c|}
\hline
&\textcolor[rgb]{0.5,0,0.5}{\textbf{Zakodowna}}\\
\textbf{Płeć}&\textcolor[rgb]{0.5,0,0.5}{\textbf{płeć}}\\\hline
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/imgf1ab254dd632767d9aa15651e494953b.png)
![LaTeX \begin{tabular}{|c|ccc|}
\hline
& \multicolumn{3}{c|}{\textbf{Zakodowane wykształcenie}}\\
\textbf{Wykształcenie}&\textcolor[rgb]{0,0,1}{\textbf{zawodowe}}&\textcolor[rgb]{1,0,0}{\textbf{średnie}}&\textcolor[rgb]{0,0.58,0}{\textbf{wyższe}}\\\hline
\cellcolor[rgb]{0.88,0.88,0.88}podstawowe&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}podstawowe&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}podstawowe&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\textcolor[rgb]{0,0,1}{zawodowe}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{zawodowe}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{zawodowe}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{zawodowe}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{1,0,0}{średnie}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{średnie}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{średnie}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{średnie}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{wyższe}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
...&...&...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img888a1cc4d1abe65cc7c2628e3f564b45.png)
Budując na podstawie zmiennych fikcyjnych, w modelu regresji wielorakiej, moglibyśmy chcieć sprawdzić jak zmienne te wpływają na pewną zmienną zależną np.  = wysokość zarobków (wyrażoną w tysiącach złotych). W wyniku takiej analizy dla każdej zmiennej fikcyjnej uzyskamy przykładowe współczynniki:
= wysokość zarobków (wyrażoną w tysiącach złotych). W wyniku takiej analizy dla każdej zmiennej fikcyjnej uzyskamy przykładowe współczynniki:
- dla płci istotny statystycznie współczynnik 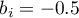 - co oznacza, że średnie zarobki kobiet są o pół tysiąca złoty niższe niż mężczyzn; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki kobiet są o pół tysiąca złoty niższe niż mężczyzn; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla wykształcenia zawodowego istotny statystycznie współczynnik 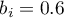 - co oznacza, że średnie zarobki osób z wykształceniem zawodowym są o 0.6 tysiąca złoty wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki osób z wykształceniem zawodowym są o 0.6 tysiąca złoty wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla wykształcenia średniego istotny statystycznie współczynnik 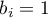 - oznacza, że średnie zarobki osób z wykształceniem średnim są o tysiąc złoty wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- oznacza, że średnie zarobki osób z wykształceniem średnim są o tysiąc złoty wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla wykształcenia wyższego istotny statystycznie współczynnik 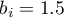 - co oznacza, że średnie zarobki osób z wykształceniem wyższym są o 1.5 tysiąca wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie.
- co oznacza, że średnie zarobki osób z wykształceniem wyższym są o 1.5 tysiąca wyższe niż dla osób z wykształceniem podstawowym; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie.
Kodowanie efektów (effect coding) jest wykorzystywane, by przy pomocy modeli wielowymiarowych odpowiedzieć na pytanie: Jak wyniki ( ), w każdej analizowanej kategorii, różnią się od wyników średniej (nieważonej) uzyskanej z próby. Kodowanie to polega na przypisaniu wartości -1 lub 1 do każdej kategorii danej zmiennej. Kategoria zakodowana jako -1 jest wówczas kategorią bazową (base)
), w każdej analizowanej kategorii, różnią się od wyników średniej (nieważonej) uzyskanej z próby. Kodowanie to polega na przypisaniu wartości -1 lub 1 do każdej kategorii danej zmiennej. Kategoria zakodowana jako -1 jest wówczas kategorią bazową (base)
- [
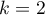 ] Gdy kodowana zmienna jest dychotomiczna, wówczas umieszczając ją w modelu regresji uzyskamy wyliczony dla niej współczynnik (
] Gdy kodowana zmienna jest dychotomiczna, wówczas umieszczając ją w modelu regresji uzyskamy wyliczony dla niej współczynnik (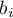 ). Współczynnik ten jest odniesieniem
). Współczynnik ten jest odniesieniem  dla kategorii 1 do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu).
dla kategorii 1 do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu).
Gdy analizowana zmienna ma więcej niż dwie kategorie, wówczas  kategorii jest reprezentowanych przez
kategorii jest reprezentowanych przez 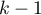 zmiennych fikcyjnych o kodowaniu efektu. Tworząc zmienne o kodowaniu efektu wybiera się kategorię dla której nie tworzy się oddzielnej zmiennej. Kategoria ta traktowana jest w modelach jako kategoria bazowa (gdyż w każdej zmiennej zapisanej poprzez kodowanie efektu odpowiadają jej wartości -1).
zmiennych fikcyjnych o kodowaniu efektu. Tworząc zmienne o kodowaniu efektu wybiera się kategorię dla której nie tworzy się oddzielnej zmiennej. Kategoria ta traktowana jest w modelach jako kategoria bazowa (gdyż w każdej zmiennej zapisanej poprzez kodowanie efektu odpowiadają jej wartości -1).
Gdy tak uzyskane zmienne 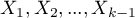 o kodowaniu efektu zostaną umieszczone w modelu regresji, wówczas zostaną dla nich wyliczone współczynniki
o kodowaniu efektu zostaną umieszczone w modelu regresji, wówczas zostaną dla nich wyliczone współczynniki  .
.
- [
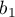 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w  ) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu);
) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu); - [
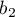 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w  ) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu);
) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu); - […]
- [
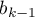 ] to odniesienie wyników
] to odniesienie wyników  (dla kodów 1 w
(dla kodów 1 w 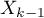 ) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu);
) do nieważonej średniej ogólnej (w korekcji o pozostałe zmienne w modelu);
Przykład
Zakodujemy przy pomocy kodowania efektu zmienną płeć o dwóch kategoriach (płeć męską wybierzemy jako kategorię bazową) i zmienną wskazującą region zamieszkania na terenie analizowanego kraju. Wyróżniono 5 regionów: północny, południowy, wschodni, zachodni i centralny - region centralny wybierzemy jako bazowy.
![LaTeX \begin{tabular}{|c|c|}
\hline
&\textcolor[rgb]{0.5,0,0.5}{\textbf{Zakodowona}}\\
\textbf{Płeć}&\textcolor[rgb]{0.5,0,0.5}{\textbf{płeć}}\\\hline
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
k&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img8517130d5e2791d315ceb261541be124.png)
![LaTeX \begin{tabular}{|c|cccc|}
\hline
\textbf{Region}& \multicolumn{4}{c|}{\textbf{Zakodowany region}}\\
\textbf{zamieszkania}&\textcolor[rgb]{0,0,1}{\textbf{zachodni}}&\textcolor[rgb]{1,0,0}{\textbf{wschodni}}&\textcolor[rgb]{0,0.58,0}{\textbf{północny}}&\textcolor[rgb]{0.55,0,0}{\textbf{południowy}}\\\hline
\cellcolor[rgb]{0.88,0.88,0.88}centralny&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}centralny&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}centralny&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\textcolor[rgb]{0,0,1}{zachodni}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{zachodni}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{zachodni}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{zachodni}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{1,0,0}{wschodni}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{wschodni}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{wschodni}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{wschodni}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{0,0.58,0}{północny}&0&0&\textcolor[rgb]{0,0.58,0}{1}&0\\
\textcolor[rgb]{0,0.58,0}{północny}&0&0&\textcolor[rgb]{0,0.58,0}{1}&0\\
\textcolor[rgb]{0.55,0,0}{południowy}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
\textcolor[rgb]{0.55,0,0}{południowy}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
\textcolor[rgb]{0.55,0,0}{południowy}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
...&...&...&...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/imgdc3ad26cbc6bbae2fa20fd348bd79e41.png)
Budując na podstawie zmiennych fikcyjnych, w modelu regresji wielorakiej, moglibyśmy chcieć sprawdzić jak zmienne te wpływają na pewną zmienną zależną np.  = wysokość zarobków (wyrażoną w tysiącach złotych). W wyniku takiej analizy dla każdej zmiennej fikcyjnej uzyskamy przykładowe współczynnik:
= wysokość zarobków (wyrażoną w tysiącach złotych). W wyniku takiej analizy dla każdej zmiennej fikcyjnej uzyskamy przykładowe współczynnik:
- dla płci istotny statystycznie współczynnik 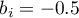 - co oznacza, że średnie zarobki kobiet są o pół tysiąca złoty niższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki kobiet są o pół tysiąca złoty niższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla regionu zachodniego istotny statystycznie współczynnik 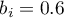 - co oznacza, że średnie zarobki osób zamieszkujących na zachodzie kraju są o 0.6 tysiąca złoty wyższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki osób zamieszkujących na zachodzie kraju są o 0.6 tysiąca złoty wyższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla regionu wschodniego istotny statystycznie współczynnik  - oznacza, że średnie zarobki osób zamieszkujących na wschodzie kraju są o tysiąc złoty niższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- oznacza, że średnie zarobki osób zamieszkujących na wschodzie kraju są o tysiąc złoty niższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla regionu północnego istotny statystycznie współczynnik 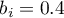 - co oznacza, że średnie zarobki osób zamieszkujących na północy są o 0.4 tysiąca wyższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- co oznacza, że średnie zarobki osób zamieszkujących na północy są o 0.4 tysiąca wyższe niż średnie zarobki w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie;
- dla regionu południowego nieistotny statystycznie współczynnik 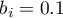 - co oznacza, że średnie zarobki osób zamieszkujących na południu nie różnią się istotnie od średnich zarobków w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie.
- co oznacza, że średnie zarobki osób zamieszkujących na południu nie różnią się istotnie od średnich zarobków w kraju; przy założeniu że pozostałe zmienne w modelu pozostają na stałym poziomie.
2014/08/22 20:00
1)
Rosenbaum P.R., Rubin D.B. (1983a), The central role of the propensity score in observational studies for causal effects. Biometrika; 70:41–55
2)
Austin P.C., (2009), The relative ability of different propensity score methods to balance measured covariates between treated and untreated subjects in observational studies. Med Decis Making; 29(6):661-77
3)
Austin P.C., (2011), An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies. Multivariate Behavioral Research 46, 3: 399–424
4)
Normand S.L. T., Landrum M.B., Guadagnoli E., Ayanian J.Z., Ryan T.J., Cleary P.D., McNeil B.J. (2001), Validating recommendations for coronary angiography following an acute myocardial infarction in the elderly: A matched analysis using propensity scores. Journal of Clinical Epidemiology; 54:387–398.
statpqpl/wielowympl/przygpl.txt · ostatnio zmienione: 2022/02/26 15:04 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


