Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:plotpl:bladpl
Wykres Blanda-Altmana
Jak zauważył Bland i Altman (19861), 19992)) w medycynie klinicznej pomiary wykonywane na żywym organiźmie ulegają ciągłym zmianom a ich prawdziwa wartość jest nieznana (np. ciśnienie tętnicze krwi), co wymaga ciągłego doskonalenia i tworzenia nowych, lepszych narzędzi ich pomiaru. Zwykle, kiedy tworzona jest nowa metoda, porównuje się jej wyniki z inną, uznaną metodą tzw. gold standard. W tym celu bada się zgodność nowej metody z metodą dotychczas stosowaną. Oczywiście, nie można oczekiwać, że nowa metoda da dokładnie ten sam wynik co metoda dotychczas wykorzystywana, ale badaczowi zależy na sprawdzeniu na ile różnią się uzyskane wyniki. By zastąpić starą metodę metodą nową, uzyskana różnica pomiędzy wynikami obu metod powinna być na tyle mała, by nie stwarzać problemu w interpretacji klinicznej. Na przykład w pomiarach ciśnienia tętniczego krwi różnica wielkości 20mmHg będzie na tyle duża, że nie może zostać uznana za dozwolony błąd, ponieważ może rzutować na zmianę decyzji o podjęciu leczenia. Metody statystyczne nie odpowiedzą na pytanie jak duża różnica metod jest dozwolona, by można było uznać metody za zgodne, ale odpowiednia ilustracja graficzna uzyskanych różnic i możliwych granic zmienności ułatwi podjęcie decyzji badaczowi.
Wykres Blanda-Altmana jest wykresem punktowym, gdzie:
- Oś X - średnia pomiarów dla porównywanych metod;
- Oś Y - różnica pomiędzy pomiarami dla porównywanych metod;
- Średnia różnic - jeśli wyniki uzyskane nową metodą są stale większe/mniejsze niż metodą starą, wówczas występuje przesunięcie, które nazywamy ang. bias, czyli linia obrazująca średnią różnic nie znajduje się na poziomie 0, ale jest przesunięta znacząco w górę lub w dół od tego poziomu.
- 95% przedział zgodności - jeśli różnice mają rozkład normalny, 95% różnic znajdzie się w przedziale (Średnia różnic
 1.96SD), gdzie SD, to odchylenie standardowe różnic.
1.96SD), gdzie SD, to odchylenie standardowe różnic.
Uwaga1! Zdefiniowany powyżej przedział zgodności nie jest tym samym co przedział ufności.
Uwaga2! Nie ma wymogu, by dane miały rozkład normalny a jedynie by rozkład różnic nie odbiegał znacznie od rozkładu normalnego. Możemy sprawdzić czy różnice mają rozkład normalny korzystając z testów badających zgodność z rozkładem normalnym lub interpretacji graficznej tego rozkładu.
- Precyzja granic przedziału zgodności - jest to przedział ufności dla granic, a więc przedział dokładności z jaką wyznaczamy granice bazując na reprezentatywnej próbie. Czym liczniejsza będzie próba i czym mniejsza będzie wariancja różnic, tym uzyskana precyzja będzie większa.
Przykład (plik ciśnieniomierz.pqs)
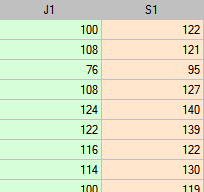
Przykład został zaczerpnięty z pracy Blanda i Altmana (19993)). Porównano w niej ciśnieniomierz półautomatyczny (S) z tradycyjnie stosowanym wcześniej klasycznym ciśnieniomierzem (J). W tym celu dokonano pomiaru ciśnienia skurczowego krwi dla 85 pacjentów przy pomocy obu ciśnieniomierzy. Fragment danych przedstawiono poniżej.
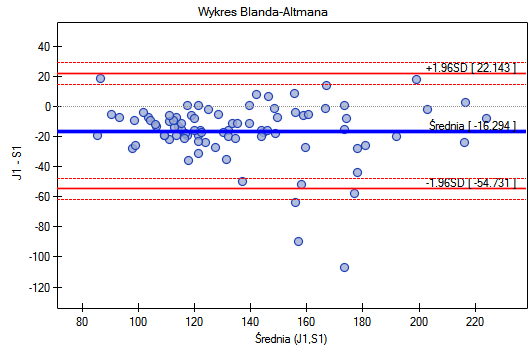
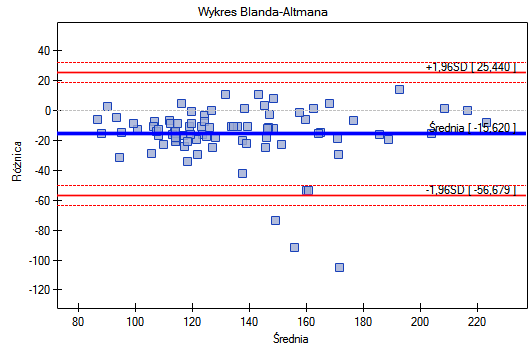
Wykres Blanda-Altmana dla zebranych danych wskazuje, że ciśnieniomierz półautomatyczny (S) daje wyższe wyniki niż klasyczny średnio o 16.3mmHG (linia dla średniej różnic znajduje się o 16.3 niżej niż bezwzględna zgodność zobrazowana linią poziomie 0). Rozpiętość przedziału zgodności wynosi aż 76.9mmHG.
Dla osób z nadciśnieniem (ciśnienie skurczowe 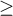 140) zmiany ciśnienia mogą być dość duże, więc badane różnice pomiarów mogą być zaburzone przez rzeczywiste skoki ciśnienia, dlatego wyodrębniono podgrupę osób z ciśnieniem w normie i nadciśnieniem na podstawie średniej wartości ciśnienia. Dla każdej podgrupy możemy wykonać wykres oddzielnie ustawiając w oknie testu filtr wielokrotny dla zmiennej grupa. Zgodność metod dla osób z ciśnieniem w normie będzie wówczas zdecydowanie lepsza (węższy przedział zgodności).
140) zmiany ciśnienia mogą być dość duże, więc badane różnice pomiarów mogą być zaburzone przez rzeczywiste skoki ciśnienia, dlatego wyodrębniono podgrupę osób z ciśnieniem w normie i nadciśnieniem na podstawie średniej wartości ciśnienia. Dla każdej podgrupy możemy wykonać wykres oddzielnie ustawiając w oknie testu filtr wielokrotny dla zmiennej grupa. Zgodność metod dla osób z ciśnieniem w normie będzie wówczas zdecydowanie lepsza (węższy przedział zgodności).
Wykres Blanda-Altmana dla powtarzanych pomiarów
Powtarzalność pomiarów jest ważnym, lecz często pomijanym aspektem w badaniu zgodności metod. Metoda o większej powtarzalności jest bardziej precyzyjna. Jeśli pomiary jednej z porównywanych metod nie są powtarzalne (tzn. powtórne pomiary wykonane na tych samych obiektach dają raczej inne wyniki), jej zgodność z inną metodą będzie niska. Jeśli powtarzalność obu metod będzie słaba, to ich zgodność będzie jeszcze niższa. W konsekwencji, gdy powtarzalność starej metody będzie słaba, zgodność nowej metody może okazać się niewielka, nawet jeśli nowa metoda charakteryzuje się wysoką powtarzalnością. Dlatego, mimo że w rzeczywistych badaniach wykonuje się jeden pomiar dla każdego obiektu (pacjenta), w badaniach mających na celu szacowanie zgodności zaleca się wykonywanie pomiarów kilkukrotnie. Takie podejście daje możliwość uwzględnienia powtarzalności uzyskanych wyników w badaniach nad zgodnością metod.
Uwaga! Jako powtarzane pomiary rozumiemy tutaj pomiary wykonywane niezależnie na tych samych obiektach, w takich samych warunkach.
Przykład c.d. (plik plik ciśnieniomierz.pqs)
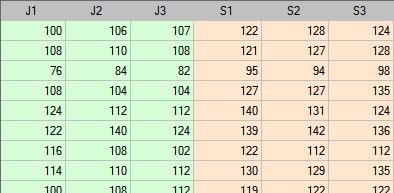
W porównaniu zgodność pomiarów dokonanych przy pomocy porównywanych ciśnieniomierzy wzięto pod uwagę również powtarzalność obu metod. Dlatego badanie powtórzono jeszcze dwukrotnie uzyskując ostatecznie dla każdego pacjenta 3 pomiary wykonane przy pomocy ciśnieniomierza półautomatycznego i 3 pomiary wykonane przy pomocy ciśnieniomierza klasycznego. Fragment danych przedstawiono poniżej.
Tym razem granice zgodności są nieco szersze niż przy wykorzystaniu pojedynczego pomiaru dla każdej metody - rozpiętość przedziału zgodności wynosi aż 82.11mmHG. Dzieje się tak dlatego, że uwzględniamy stopień powtarzalności pomiarów. Niestety, uwzględnienie kilku powtórzeń zwiększa szerokość granic, ale przedstawione wyniki lepiej reprezentują rzeczywistość. Nie uwzględniając bowiem stopnia powtarzalności zakładamy, że powtarzalność jest 100 procentowa, co w rzeczywistych warunkach jest niemal niemożliwe.
Podobnie jak poprzednio, zaleca się powtórzyć analizę oddzielnie dla osób z nadciśnieniem i z ciśnieniem w normie.
statpqpl/plotpl/bladpl.txt · ostatnio zmienione: 2021/01/13 17:38 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

