Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown3grpl:nparpl:anova_friepl
ANOVA Friedmana
Analiza wariancji powtarzanych pomiarów dla rang Friedmana, czyli ANOVA Friedmana (ang. Friedman repeated measures analysis of variance by ranks) opisana została przez Friedmana (1937)1). Test ten stosuje się w sytuacji, gdy pomiarów badanej zmiennej dokonujemy kilkukrotnie (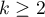 ) w różnych warunkach. Stosowana jest również, gdy dysponujemy rankingami pochodzącymi z różnych źródeł (od różnych sędziów) i dotyczącymi kilku (
) w różnych warunkach. Stosowana jest również, gdy dysponujemy rankingami pochodzącymi z różnych źródeł (od różnych sędziów) i dotyczącymi kilku (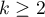 ) obiektów a zależy nam na ocenie zgodności tych rankingów.
) obiektów a zależy nam na ocenie zgodności tych rankingów.
Iman Davenport (19802)) pokazał, że w wielu przypadkach statystka Friedmana jest nadmiernie konserwatywna i dokonał pewnej jej modyfikacji. Modyfikacja ta jest nieparametrycznym odpowiednikiem ANOVA powtarzanych pomiarów co sprawia, że jest obecnie rekomendowana do stosowania w zastępstwie tradycyjnej statystyki Friedmana.
Dodatkowe analizy:
- możliwe jest uwzględnienie braków danych poprzez opcje
Akceptuj braki danych, wyliczając ANOVA Durbina lub ANOVA Skillings-Mack; - możliwe jest testowanie trendu w ułożeniu badanych grup poprzez wykonanie testu Page dla trendu.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości sumy rang dla kolejnych pomiarów lub są upraszczane do median:
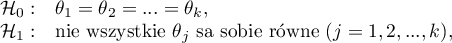
gdzie:
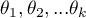 mediany badanej cechy w kolejnych pomiarach z badanej populacji.
mediany badanej cechy w kolejnych pomiarach z badanej populacji.
Wyznacza się dwie statystyki testowe: statystykę Friedmana i modyfikację Imana-Davenport tej statystyki.
Statystyka Friedmana ma postać:
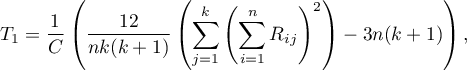
gdzie:

 liczność próby,
liczność próby,
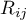
 rangi przypisane kolejnym pomiarom
rangi przypisane kolejnym pomiarom  , oddzielnie dla każdego z badanych obiektów
, oddzielnie dla każdego z badanych obiektów 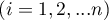 ,
,
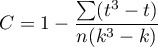
 korekta na rangi wiązane,
korekta na rangi wiązane,

 liczba przypadków wchodzących w skład rangi wiązanej.
liczba przypadków wchodzących w skład rangi wiązanej.
Modyfikacjia Imana-Davenport statystyki Friedmana ma postać:
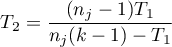
Wzór na statystykę 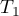 i
i 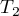 zawiera poprawkę na rangi wiązane
zawiera poprawkę na rangi wiązane  . Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 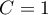 ).
).
Statystyka 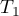 ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z
ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 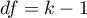 stopniami swobody.
stopniami swobody.
Statystyka 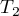 podlega rozkładowi F Snedecora z
podlega rozkładowi F Snedecora z 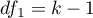 i
i  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Stosowany dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
Test Dunna (Dunn 19643)) jest testem korygowanym ze względu na wielokrotne testowanie. Najczęściej wykorzystuje się tu korektę Bonferroniego lub Sidaka, chociaż dostępne są również inne, nowsze korekty opisane szerzej w dziale Wielokrotne porównania.
Przykład - porównania proste (porównanie pomiędzy sobą 2 wybranych median / średnich rang):
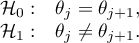
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
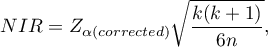
gdzie:
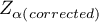 - to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności
- to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności  skorygowanego o liczbę możliwych porównań prostych
skorygowanego o liczbę możliwych porównań prostych  zgodnie z wybraną poprawką.
zgodnie z wybraną poprawką.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
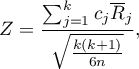
gdzie:
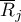
 średnia rang
średnia rang  -tego pomiaru, dla
-tego pomiaru, dla  ,
,
Statystyka ta ma asymptotycznie (dla dużych liczności próby) rozkład normalny, a wartość p jest korygowana o liczbę możliwych porównań prostych zgodnie z wybraną poprawką.
Nieparametryczny odpowiednik LSD Fishera4), stosowany dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
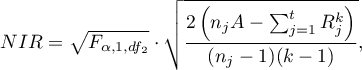
gdzie:
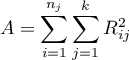
 suma kwadratów dla rang,
suma kwadratów dla rang,
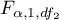 to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz dla stopni swobody odpowiednio: 1 i
oraz dla stopni swobody odpowiednio: 1 i 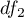 .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
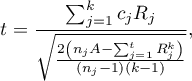
gdzie:
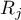 - suma rang
- suma rang  -tego pomiaru, dla
-tego pomiaru, dla  ,
,
Statystyka ta podlega rozkładowi t-Studenta z 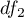 stopniami swobody.
stopniami swobody.
Okno z ustawieniami opcji ANOVA Friedmana wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Friedmana (możliwość braków danych) lub poprzez Kreator.
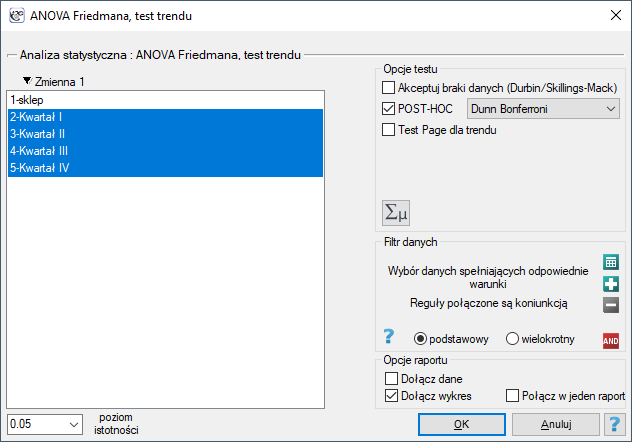
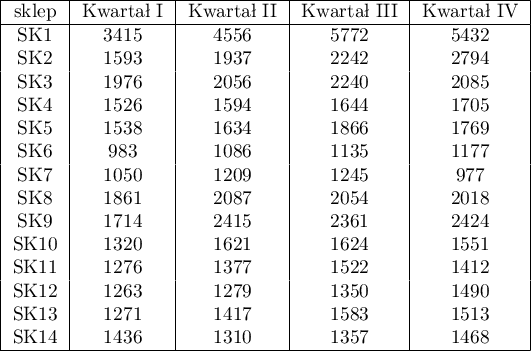
Badano kwartalną wielkość sprzedaży pewnego batonu czekoladowego w 14 losowo wybranych marketach. Badanie rozpoczęto w styczniu a zakończono w grudniu. W czasie drugiego kwartału trwała intensywna billboardowa kampania reklamowa tego produktu. Sprawdzimy, czy kampania miała wpływ na wielkość sprzedaży reklamowanego batonu.
Hipotezy:

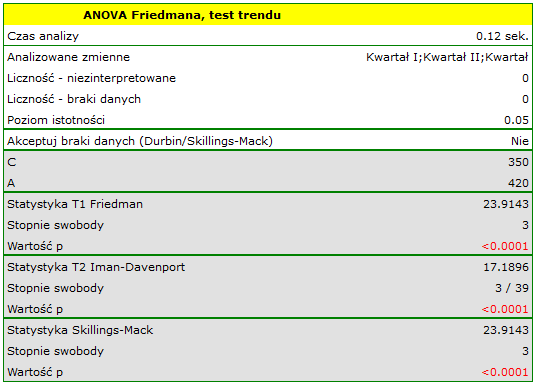
Porównując wartość p testu Friedmana (jak i wartość p korekty Iman-Davenport testu Friedmana) z poziomem istotności  , stwierdzamy, że sprzedaż batonu nie jest taka sama w każdym kwartale. Wykonana analiza POST-HOC Dunna z korektą Bonferroniego wskazuje na różnice wielkości sprzedaży dotyczące kwartału I i III oraz I i IV, a analogiczna analiza przeprowadzona silniejszym testem Conover-Iman wskazuje na różnice pomiędzy wszystkimi kwartałami za wyjątkiem kwartału III i IV.
, stwierdzamy, że sprzedaż batonu nie jest taka sama w każdym kwartale. Wykonana analiza POST-HOC Dunna z korektą Bonferroniego wskazuje na różnice wielkości sprzedaży dotyczące kwartału I i III oraz I i IV, a analogiczna analiza przeprowadzona silniejszym testem Conover-Iman wskazuje na różnice pomiędzy wszystkimi kwartałami za wyjątkiem kwartału III i IV.
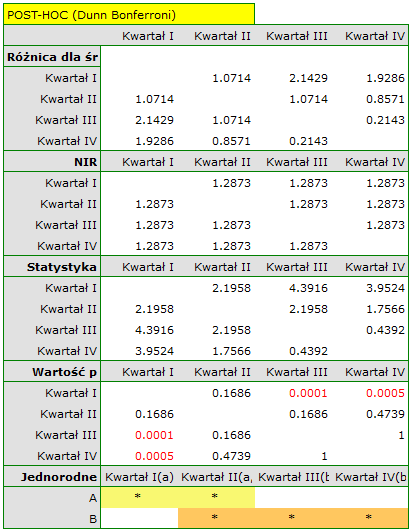
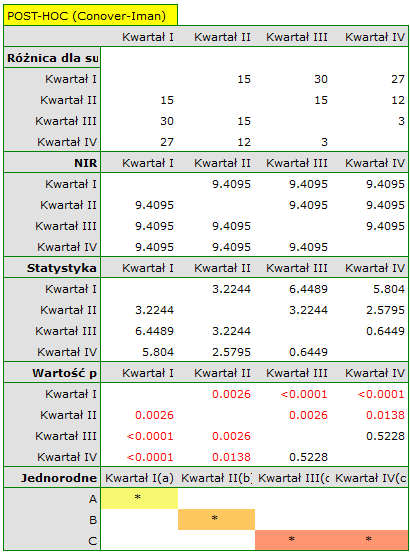
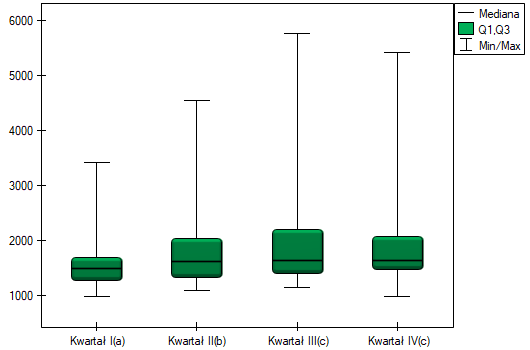
Na wykresie przedstawiliśmy grupy jednorodne wyznaczone testem Conover-Iman.
Dokładny opis danych możemy przedstawić wybierając w oknie analizy statystyki opisowe 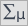 .
.
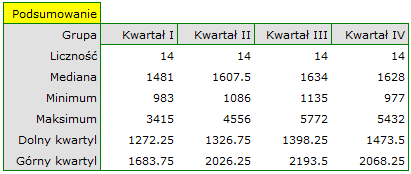
Gdyby dane były opisane skalą porzadkową o niewielu kategoriach, warto by było przedstawić je rownież w licznościach i procentach. W naszym przykładzie nie byłaby to dobra metoda opisu.
1)
Friedman M. (1937), The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association, 32,675-701
2)
Iman R. L., Davenport J. M. (1980), Approximations of the critical region of the friedman statistic, Communications in Statistics 9, 571–595
3)
Dunn O. J. (1964), Multiple comparisons using rank sums. Technometrics, 6: 241–252
4)
Conover W. J. (1999), Practical nonparametric statistics (3rd ed). John Wiley and Sons, New York
statpqpl/porown3grpl/nparpl/anova_friepl.txt · ostatnio zmienione: 2022/01/23 21:10 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


