Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown3grpl:nparpl:pagepl
Test Page dla trendu
Test Page dla trendu (ang. the Page test for ordered alternative) opisany w roku 1963 przez Page E. B. 1) może być wyliczany w takiej samej sytuacji jak ANOVA Friedmana, gdyż bazuje na tych samych założeniach. Test Page inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu w kolejnych pomiarach.
Hipotezy dotyczą równości sumy rang dla kolejnych pomiarów lub są upraszczane do median:
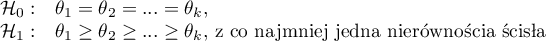
Uwaga!
Określenie: „z co najmniej jedną nierównością ścisłą” zapisane w hipotezie alternatywnej tego testu oznacza, że co najmniej jedna mediana powinna być większa niż mediana innej grupy pomiarów w kolejności określonej.
Statystyka testowa ma postać:
![LaTeX \begin{displaymath}
Z=\frac{L-\left[\frac{nk(k+1)^2}{4}\right]}{\sqrt{\frac{n(k^3-k)^2}{144(k-1)}}}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/imgd8f373e9725654f26c78c01931a87148.png)
gdzie:
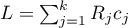 ,
,
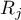
 suma rang
suma rang  -tego pomiaru,
-tego pomiaru,
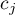
 waga dla
waga dla  -tego pomiaru informująca o naturalnym porządku tego pomiaru w śród innych pomiarów (wagi to kolejne liczby naturalne).
-tego pomiaru informująca o naturalnym porządku tego pomiaru w śród innych pomiarów (wagi to kolejne liczby naturalne).
Uwaga!
By można było przeprowadzić analizę trendu, należy wskazać oczekiwane uporządkowanie pomiarów przypisując kolejne liczby naturalne kolejnym grupom pomiarowym. Liczby te w analizie traktowane są jako wagi 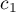 ,
, 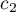 , …,
, …, 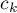 .
.
Wzór na statystykę testową  nie zawiera poprawki na rangi wiązane, przez co staje się nieco bardziej konserwatywny, gdy rangi wiązane występują. Jednakże stosowanie korekty na rangi wiązane w przypadku tego testu nie jest rekomendowane.
nie zawiera poprawki na rangi wiązane, przez co staje się nieco bardziej konserwatywny, gdy rangi wiązane występują. Jednakże stosowanie korekty na rangi wiązane w przypadku tego testu nie jest rekomendowane.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Przy znanym oczekiwanym kierunku trendu, hipoteza alternatywna jest jednostronna i interpretacji podlega jednostronna wartość  . Interpretacja dwustronnej wartości
. Interpretacja dwustronnej wartości  oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość
oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji testu Page wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Friedmana (możliwość braków danych) lub poprzez Kreator.
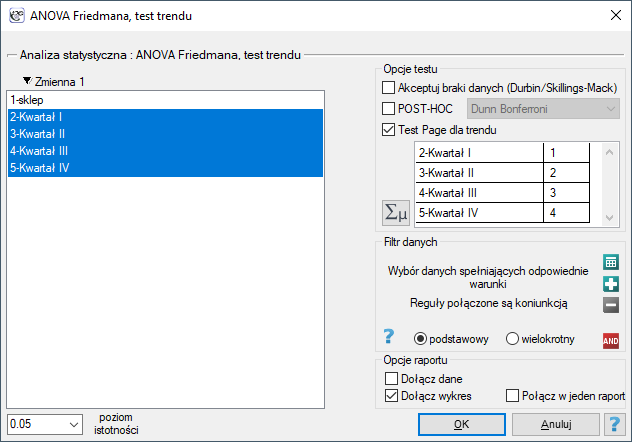
Przykład c.d. (plik baton.pqs)
Oczekiwanym skutkiem prowadzenia przez firmę intensywnej kampanii reklamowej jest stały wzrost sprzedaży oferowanego batonu.
Hipotezy:
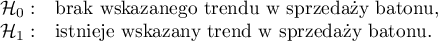
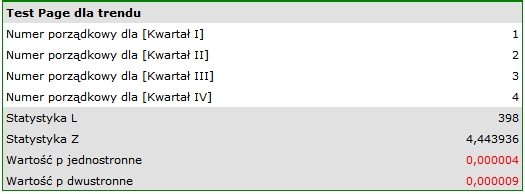
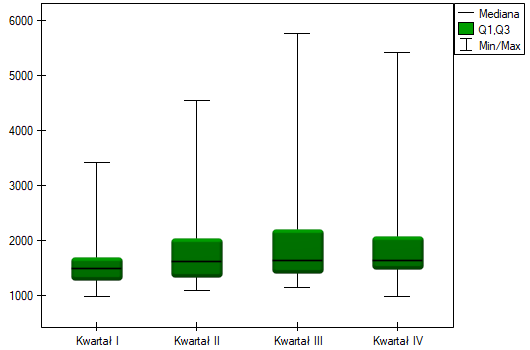
Porównując jednostronną wartość 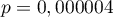 z poziomem istotności
z poziomem istotności  , stwierdzamy, że kampania przyniosła oczekiwany trend wzrostu sprzedaży produktu.
, stwierdzamy, że kampania przyniosła oczekiwany trend wzrostu sprzedaży produktu.
1)
Page E. B. (1963), Ordered hypotheses for multiple treatments: A significance test for linear ranks. Journal of the American Statistical Association 58 (301): 216–30
statpqpl/porown3grpl/nparpl/pagepl.txt · ostatnio zmienione: 2021/02/04 20:58 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


