Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown3grpl:nparpl:skillings_mpl
ANOVA Skillings-Mack (brakujących danych)
Analiza wariancji powtarzanych pomiarów dla rang Skillings-Mack została zaproponowana przez Skillings'a i Mack'a w roku 1981 1). Jest to test, który może być wykorzystywany w przypadku występowania braków danych, ale braki te nie muszą występować w żadnym szczególnym układzie. Każdy obiekt musi mieć jednak przynajmniej dwie obserwacje. Jeśli nie ma rang wiązanych a braki nie występują jest tożsamy z ANOVA Friedmana, a jeśli braki danych występują w układzie zbalansowanym odpowiada wynikom ANOVA Durbina.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości sumy rang dla kolejnych pomiarów (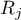 ) lub są upraszczane do median (
) lub są upraszczane do median (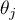 ):
):
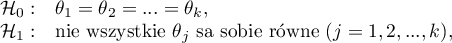
Statystyka testowa ma postać:
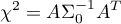
gdzie:
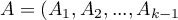
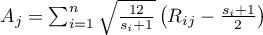 ,
,
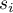 - liczba obserwacji dla
- liczba obserwacji dla  -tego obiektu,
-tego obiektu,
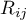 - rangi przypisane kolejnym pomiarom (
- rangi przypisane kolejnym pomiarom (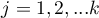 ), oddzielnie dla każdego z badanych obiektów (
), oddzielnie dla każdego z badanych obiektów (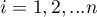 ), przy czym rangi dla braków danych równe są średniej randze dla danego obiektu,
), przy czym rangi dla braków danych równe są średniej randze dla danego obiektu,
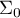 - macierz wyznaczająca kowariancje dla
- macierz wyznaczająca kowariancje dla  przy prawdziwości
przy prawdziwości  2).
2).
Gdy każda para pomiarów występuje równocześnie dla przynajmniej jednej obserwacji, statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 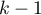 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji ANOVA Skillings-Mack wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Friedmana (możliwość braków danych) lub poprzez Kreator.
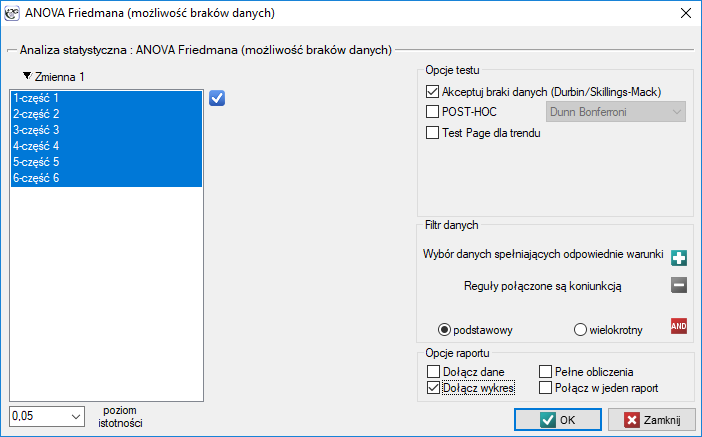
Uwaga!
By rekordy w których występują braki danych były brane pod uwagę wymagane jest zaznaczenie opcji Akceptuj braki danych. Jako braki danych traktowane są puste komórki oraz komórki o wartościach nieliczbowych. W analizie biorą udział tylko rekordy zawierające więcej niż jedną wartość liczbową.
Przykład (plik ankietyzacja.pqs)
Pewien nauczyciel akademicki, chcąc poprawić sposób prowadzenia zajęć postanowił zweryfikować swoje umiejętności dydaktyczne. W kilku losowo wybranych grupach studenckich, podczas ostatnich zajęć, prosił o wypełnienie krótkiej anonimowej ankiety. Ankieta składała się z 6 pytań dotyczących sposobu ilustrowania sześciu wyszczególnionych partii materiału. Studenci mogli dokonać oceny w skali pięciostopniowej , gdzie 1-zupełnie niezrozumiały sposób przedstawiana materiału, 5 - bardzo jasny i ciekawy sposób ilustrowania materiału. Uzyskane w ten sposób dane okazały się nie być kompletne ze względu na brak odpowiedzi studentów na pytania dotyczące tej części materiału, na której byli nieobecni. W 30-osobowej grupie wypełniającej ankietę, tylko 15 osób udzieliło kompletu odpowiedzi. Wykonanie analizy nie uwzględniającej braków danych (w tym przypadku analizy Friedmana) będzie miało ograniczoną moc poprzez tak drastyczne obcięcie liczności grupy i nie doprowadzi do wykrycia istotnych różnic. Braki danych nie były zaplanowane i nie występują w bloku zbalansowanym, a więc nie można wykonać tego zadania przy użyciu analizy Durbina wraz z jego testem POST-HOC.
Hipotezy:

Wyniki analizy ANOVA Skillings-Mack przedstawia następujący raport:
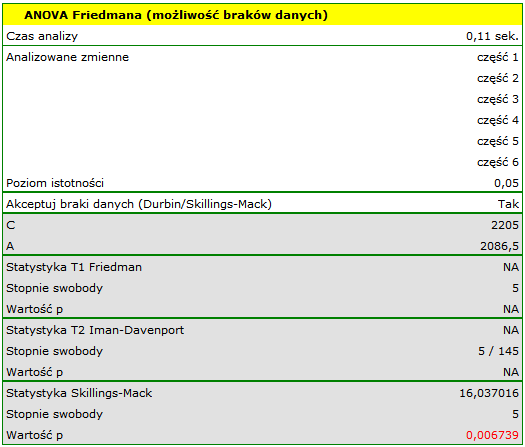
Uzyskaną wartość  należy traktować ostrożnie ze względu na możliwe rangi wiązane. Jednak w przypadku tego badania wartość
należy traktować ostrożnie ze względu na możliwe rangi wiązane. Jednak w przypadku tego badania wartość 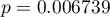 znajduje się znacznie poniżej przyjętego poziomu istotności
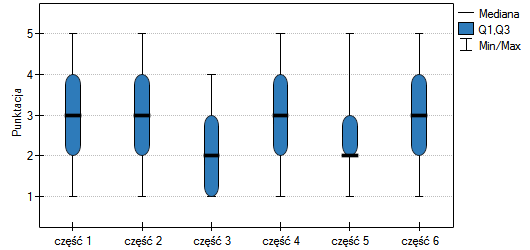
znajduje się znacznie poniżej przyjętego poziomu istotności  , co świadczy o występowaniu istotnych różnic. Różnice w odpowiedziach można obserwować na wykresie, nie ma jednak możliwości przeprowadzenia analizy POST-HOC dla tego testu.
, co świadczy o występowaniu istotnych różnic. Różnice w odpowiedziach można obserwować na wykresie, nie ma jednak możliwości przeprowadzenia analizy POST-HOC dla tego testu.
statpqpl/porown3grpl/nparpl/skillings_mpl.txt · ostatnio zmienione: 2022/02/13 17:17 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


