Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Porównanie - 2 grupy » Testy nieparametryczne
Pasek boczny
statpqpl:porown2grpl:nparpl
Spis treści
Testy nieparametryczne
Test U Manna-Whitneya
Test U Manna-Whitneya (ang. Mann-Whitney U test) znany jest również jako test Wilcoxona Manna-Whitneya (ang. Wilcoxon Mann-Whitney test), Mann i Whitney (1947)1) oraz Wilcoxon (1949)2). Test ten służy do weryfikacji hipotezy o braku przesunięcia porównywanych rozkładów tzn. najczęsciej nieistotności różnic pomiędzy medianami badanej zmiennej w dwóch populacjach (przy czym zakładamy, że rozkłady zmiennej są sobie bliskie - porównanie wariancji rang można sprawdzić testem dla rang Conovera).
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości średnich rang dla porównywanych populacji lub są upraszczane do median:
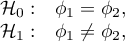
gdzie:
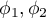 to rozkłady badanej zmiennej w pierwszej i drugiej populacji.
to rozkłady badanej zmiennej w pierwszej i drugiej populacji.
Wyznaczamy wartość statystyki testowej, a na jej podstawie wartość  , którą porównujemy z poziomem istotności
, którą porównujemy z poziomem istotności  :
:

Uwaga!
W zależności od wielkości próby statystyka testowa przyjmuje inną postać:
- Dla małej liczności próby
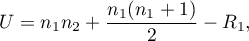
lub
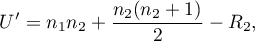
gdzie 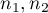 to liczności prób,
to liczności prób, 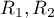 to sumy rang dla prób.
to sumy rang dla prób.
Standardowo interpretacji podlega mniejsza z wartości 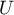 lub
lub 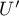 .
.
Statystyka ta podlega rozkładowi Manna-Whitneya i nie zawiera poprawki na rangi wiązane. Wartość dokładnego prawdopodobieństwa z rozkładu Manna-Whitneya wyliczana jest z dokładnością do części setnej ułamka.
- Dla próby o dużej liczności
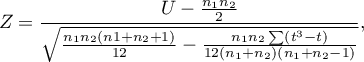
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 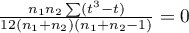 )
)
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Poprawka na ciągłość testu Manna-Whitneya (Marascuilo and McSweeney (1977)3))
Poprawkę na ciągłość stosujemy by zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu normalnego. Wzór na statystykę testową z poprawką na ciągłość wyraża się wtedy:
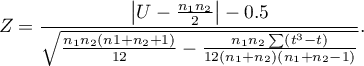
Standaryzowana wielkość efektu
Rozkład statystyki testu Manna-Whitneya jest aproksymowany przez rozkłady normalny, który można przekształcić na wielkość efektu 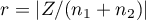 4) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
4) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
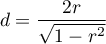
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 5) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu U Manna-Whitneya wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Mann-Whitney lub poprzez ''Kreator''.
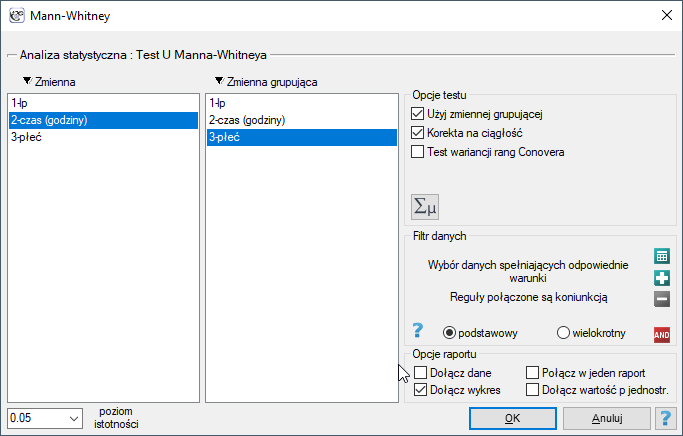
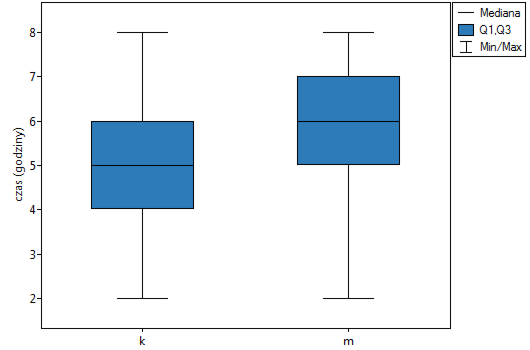
Wysunięto hipotezę, że na pewnej uczelni studenci matematyki spędzają statystycznie więcej czasu przed komputerem niż studentki matematyki. W celu weryfikacji tego przypuszczenia z populacji osób studiujących matematykę na tej uczelni wylosowano próbę liczącą 54 osoby (25 kobiet i 29 mężczyzn). Osoby te zapytano o to jak dużo czasu dziennie spędzają przy komputerze (czas w godzinach) i otrzymano następujące wyniki:
(czas, płeć): (2, k) (2, m) (2, m) (3, k) (3, k) (3, k) (3, k) (3, m) (3, m) (4, k) (4, k) (4, k) (4, k) (4, m) (4, m) (5, k) (5, k) (5, k) (5, k) (5, k) (5, k) (5, k) (5, k) (5, k) (5, m) (5, m) (5, m) (5, m) (6, k) (6, k) (6, k) (6, k) (6, k) (6, m) (6, m) (6, m) (6, m) (6, m) (6, m) (6, m) (6, m) (7, k) (7, m) (7, m) (7, m) (7, m) (7, m) (7, m) (7, m) (7, m) (7, m) (8, k) (8, m) (8, m).}
Hipotezy:


Na podstawie przyjętego poziomu  i statystyki
i statystyki  testu Manna-Whitneya bez poprawki na ciągłość (
testu Manna-Whitneya bez poprawki na ciągłość ( =0.015441) jak i z tą poprawką
=0.015441) jak i z tą poprawką 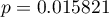 , jak też na podstawie dokładnej statystyki
, jak też na podstawie dokładnej statystyki 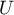 (
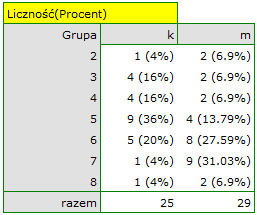
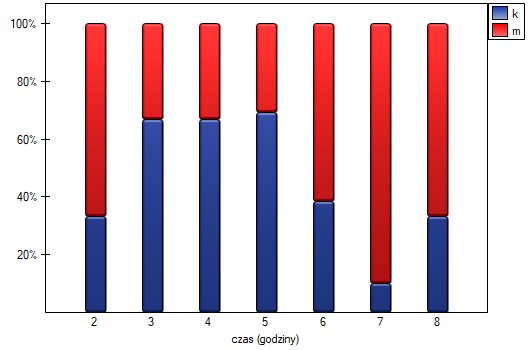
( =0.014948) możemy przyjąć, że istnieją ważne statystycznie różnice pomiędzy studentkami a studentami matematyki w ilości czasu spędzanego przed komputerem. Różnice te polegają na tym, że studentki spędzają mniej czasu przed komputerem niż studenci. Opisać je można na podstawie mediany, kwartyli oraz wartości największej i najmniejszej, które widzimy również na wykresie typu ramka-wąsy. Innym sposobem opisu różnic jest przedstawienie czasu spędzonego przed komputerem na podstawie tabeli liczności i procentów (które uruchamiamy w oknie analizy ustawiając statystyki opisowe
=0.014948) możemy przyjąć, że istnieją ważne statystycznie różnice pomiędzy studentkami a studentami matematyki w ilości czasu spędzanego przed komputerem. Różnice te polegają na tym, że studentki spędzają mniej czasu przed komputerem niż studenci. Opisać je można na podstawie mediany, kwartyli oraz wartości największej i najmniejszej, które widzimy również na wykresie typu ramka-wąsy. Innym sposobem opisu różnic jest przedstawienie czasu spędzonego przed komputerem na podstawie tabeli liczności i procentów (które uruchamiamy w oknie analizy ustawiając statystyki opisowe 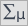 ) lub na podstawie wykresu kolumnowego.
) lub na podstawie wykresu kolumnowego.
2014/08/22 20:00
Test Wilcoxona (kolejności par)
Test kolejności par Wilcoxona (ang. Wilcoxon matched-pairs test), znany również pod nazwą testu Wilcoxona dla grup zależnych, Wilcoxon (19456),19497)). Stosuje się go w sytuacji gdy pomiarów badanej zmiennej dokonujemy dwukrotnie w różnych warunkach. Jest on rozszerzeniem na dwie zależne próby testu rangowanych znaków Wilcoxona (przeznaczonego dla jednej próby). Interesuje nas różnica pomiędzy parami pomiarów badanej cechy (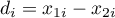 ) dla każdego z
) dla każdego z  badanych obiektów. Różnica ta wykorzystywana jest do weryfikacji hipotezy o tym, że mediana dla niej (dla różnicy) w badanej populacji wynosi 0.
badanych obiektów. Różnica ta wykorzystywana jest do weryfikacji hipotezy o tym, że mediana dla niej (dla różnicy) w badanej populacji wynosi 0.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości sumy rang dodatnich i ujemnych lub są upraszczane do median:
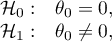
gdzie:
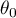 to - mediana
to - mediana 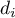 w populacji.
w populacji.
Wyznaczamy wartość statystyki testowej, a na jej podstawie wartość  , którą porównujemy z poziomem istotności
, którą porównujemy z poziomem istotności  :
:

Uwaga!
W zależności od wielkości próby statystyka testowa przyjmuje inną postać:
- Dla małej liczności próby
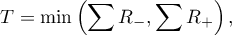
Statystyka ta podlega rozkładowi Wilcoxona i nie zawiera poprawki na rangi wiązane.
- Dla próby o dużej liczności
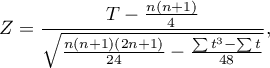
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 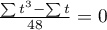 ).
).
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Poprawka na ciągłość testu Wilcoxona (Marascuilo and McSweeney (1977)8))
Poprawkę na ciągłość stosujemy by zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu normalnego. Wzór na statystykę testową z poprawką na ciągłość wyraża się wtedy wzorem:
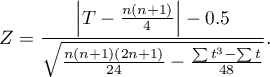
Uwaga! Od wersji 1.8.0 mediana wyliczana w dla kolumny różnica obejmuje wszystkie pary wyników za wyjątkiem tych, których różnica wynosi 0.
Standaryzowana wielkość efektu
Rozkład statystyki testu Wilcoxona jest aproksymowany przez rozkłady normalny, który można przekształcić na wielkość efektu 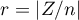 9) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
9) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
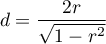
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 10) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu Wilcoxona dla grup zależnych wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Wilcoxon (kolejności par) lub poprzez ''Kreator''.
Pobrano próbę 22 pacjentów cierpiących na raka. Badano u nich poziom odczuwanego bólu (na skali od 1 do 10, gdzie 1 to brak bólu a 10 to ból największy). Badanie to powtórzono po miesiącu stosowania kuracji nowym lekiem mającym obniżyć poziom odczuwanego bólu. Otrzymano następujące wyniki:
(przed, po): (2, 2) (2, 3) (3, 1) (3,1) (3, 2) (3, 2) (3, 3) (4, 1) (4, 3) (4, 4) (5, 1) (5, 1) (5, 2) (5, 4) (5, 4) (6, 1) (6, 3) (7, 2) (7, 4) (7, 4) (8, 1) (8, 3). Chcemy sprawdzić, czy zastosowana kuracja ma wpływ na poziom odczuwanego bólu w populacji z której pochodzi próba.
Hipotezy:

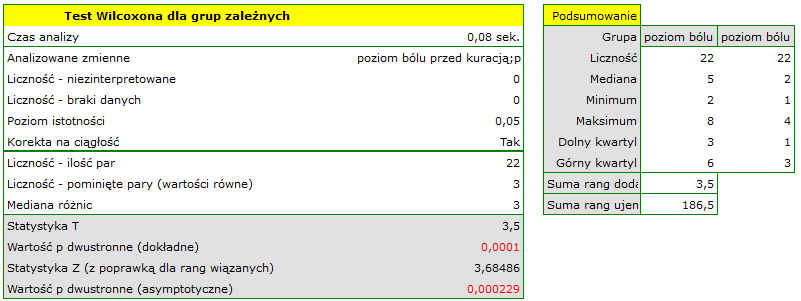
Porównując wartość 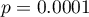 testu Wilcoxona opartego o statystykę
testu Wilcoxona opartego o statystykę 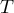 z poziomem istotności
z poziomem istotności  stwierdzamy, że istnieje ważna statystycznie różnica w poziomie odczuwanego bólu pomiędzy dwoma badaniami. Różnica te polega na tym, że poziom bólu spadł (suma rang ujemnych jest znacznie większa niż suma rang dodatnich). Taką samą decyzję podjęlibyśmy również na podstawie wartości
stwierdzamy, że istnieje ważna statystycznie różnica w poziomie odczuwanego bólu pomiędzy dwoma badaniami. Różnica te polega na tym, że poziom bólu spadł (suma rang ujemnych jest znacznie większa niż suma rang dodatnich). Taką samą decyzję podjęlibyśmy również na podstawie wartości 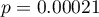 lub
lub 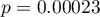 testu Wilcoxona opartego o statystykę
testu Wilcoxona opartego o statystykę  lub
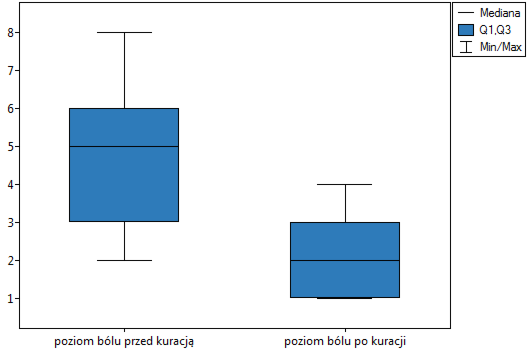
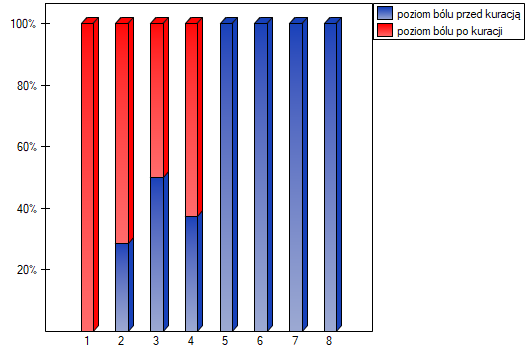
lub  z poprawką na ciągłość. Różnice możemy zaobserwować na wykresie typu ramka-wąsy lub wykresie kolumnowym.
z poprawką na ciągłość. Różnice możemy zaobserwować na wykresie typu ramka-wąsy lub wykresie kolumnowym.

2014/08/22 20:00
Testy chi-kwadrat
Testy te opierają się na danych zebranych w postaci tabeli kontyngencji 2 cech, cechy X i cechy Y, z których pierwsza ma  a druga
a druga  kategorii, a więc powstała tabela ma
kategorii, a więc powstała tabela ma  wierszy i
wierszy i  kolumn. Z tego względu możemy mówić o teście chi-kwadrat 2×2 (dla tabel o dwóch wierszach i dwóch kolumnach) lub o teście chi-kwadrat RxC (o wielu wierszach i kolumnach).
kolumn. Z tego względu możemy mówić o teście chi-kwadrat 2×2 (dla tabel o dwóch wierszach i dwóch kolumnach) lub o teście chi-kwadrat RxC (o wielu wierszach i kolumnach).
Szczegółowe informacje na temat testu chi-kwadrat dwóch cech możemy przeczytać tutaj:
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
Dodatkowy warunek dla testu  :
:
Hipotezy w brzmieniu ogólnym:
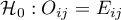 dla wszystkich kategorii,
dla wszystkich kategorii,
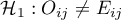 dla przynajmniej jednej kategorii.
dla przynajmniej jednej kategorii.
gdzie:
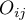
 liczności obserwowane w tabeli kontyngencji,
liczności obserwowane w tabeli kontyngencji,
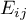
 liczności oczekiwane w tabeli kontyngencji.
liczności oczekiwane w tabeli kontyngencji.
Hipotezy w brzmieniu testu niezależności:
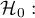 nie istnieje zależność pomiędzy badanymi cechami populacji (obie klasyfikacje ze względu na cechę X i na cechę Y są statystycznie niezależne),
nie istnieje zależność pomiędzy badanymi cechami populacji (obie klasyfikacje ze względu na cechę X i na cechę Y są statystycznie niezależne),
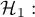 istnieje zależność pomiędzy badanymi cechami populacji.
istnieje zależność pomiędzy badanymi cechami populacji.
Wyznaczoną wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo
Oprócz testu chi-kwadrat może zajść konieczność wyznaczenia innego, pokrewnego testu. W przypadku gdy warunek Cochrana nie jest spełniony można wyznaczyć:
W przypadku gdy uzyskamy tabelę Rx2, i kategorie R można uporządkować, możliwe jest wyznaczanie trendu:
W przypadku, gdy na podstawie testu wykonanego dla tabeli większej niż 2×2 stwierdzimy występowanie istotnych zależności lub różnic, wówczas można wykonać wielokrotne porównania wraz z odpowiednią korektą porównań wielokrotnych po to, by zlokalizować umiejscowienie tych zależności/różnic. Korekta taka może być dokonana automatycznie, gdy tabela ma wiele kolumn. Wówczas w oknie opcji testu należy zaznaczyć
Wielokrotne porównania kolumn (RxC).W przypadku, gdy chcemy opisać siłę związku między cechą X i cechą Y możemy wyznaczyć:
W przypadku, gdy chcemy opisać dla tabel 2×2 wielkość wpływu czynnika ryzyka możemy wyznaczyć:
2020/10/06 12:43
· admin
Test chi-kwadrat dla dużych tabel
Test ten opierają się na danych zebranych w postaci tabeli kontyngencji 2 cech ( ,
,  ), z których pierwsza ma możliwe
), z których pierwsza ma możliwe  kategorii
kategorii 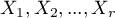 a druga
a druga  kategorii
kategorii 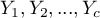 .
.
Test  dla tabel
dla tabel 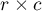 znany jest również pod nazwą testu
znany jest również pod nazwą testu  Pearsona (ang. Pearson's Chi-square test), Karl Pearson 1900. Test ten jest rozszerzeniem na 2 cechy testu chi-kwadrat (dobroci dopasowania).
Statystyka testowa ma postać:
Pearsona (ang. Pearson's Chi-square test), Karl Pearson 1900. Test ten jest rozszerzeniem na 2 cechy testu chi-kwadrat (dobroci dopasowania).
Statystyka testowa ma postać:
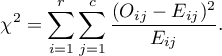
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 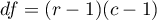 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności poziomem istotności
porównujemy z poziomem istotności poziomem istotności  .
.
Okno z ustawieniami opcji testu Chi-kwadrat (RxC) wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher, OR/RR lub poprzez ''Kreator''.
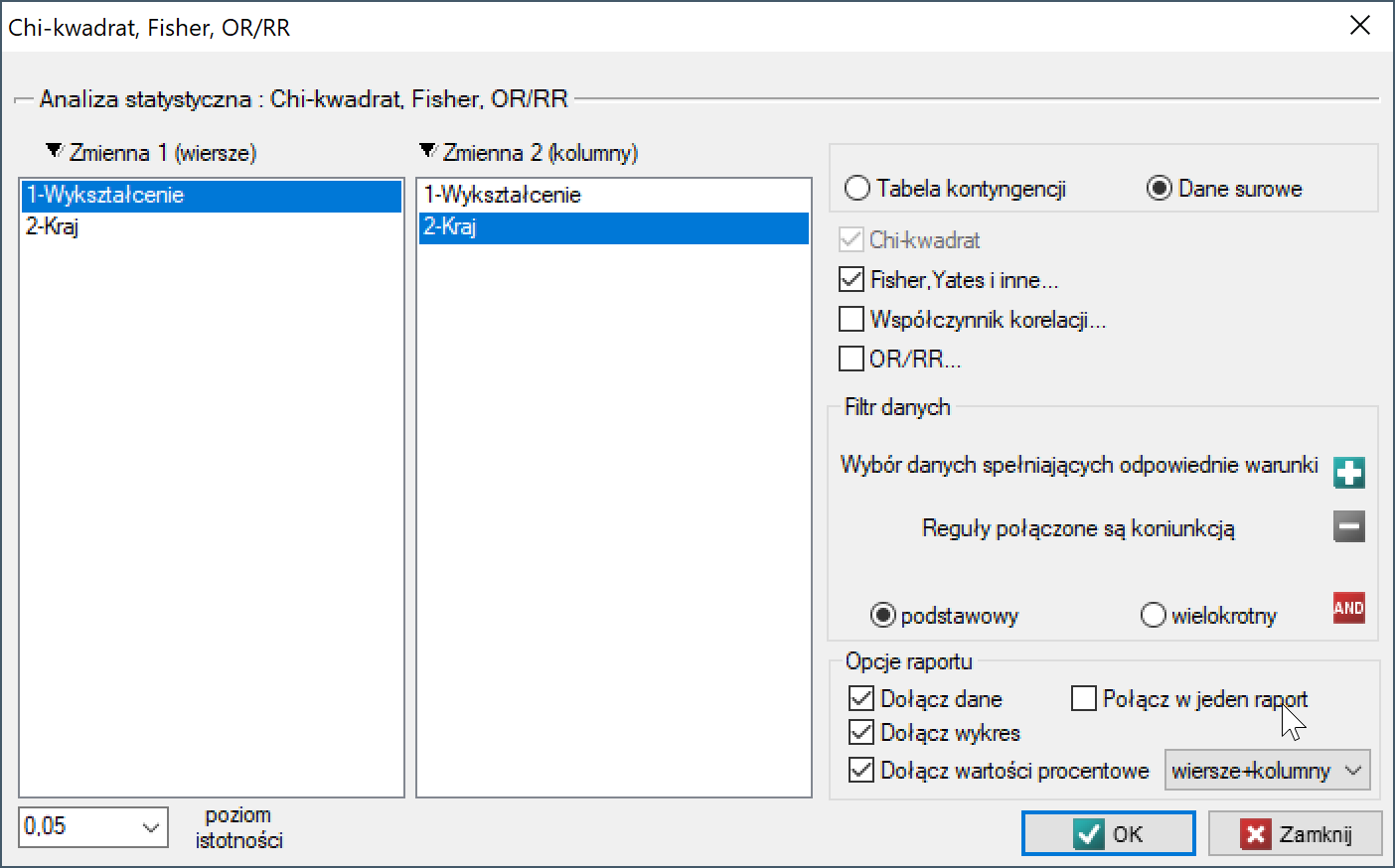
Przykład (plik kraj-wykształcenie.pqs)
Rozpatrujemy próbę 605 osób (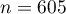 ), dla których badamy 2 cechy (
), dla których badamy 2 cechy ( =kraj zamieszkania,
=kraj zamieszkania,  =wykształcenie). Pierwsza cecha występuje w 4, a druga w 3 kategoriach (
=wykształcenie). Pierwsza cecha występuje w 4, a druga w 3 kategoriach ( =Kraj 1,
=Kraj 1,  =Kraj 2,
=Kraj 2, 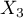 =Kraj 3,
=Kraj 3, 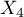 =Kraj 4,
=Kraj 4, 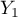 =podstawowe,
=podstawowe, 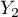 =średnie,
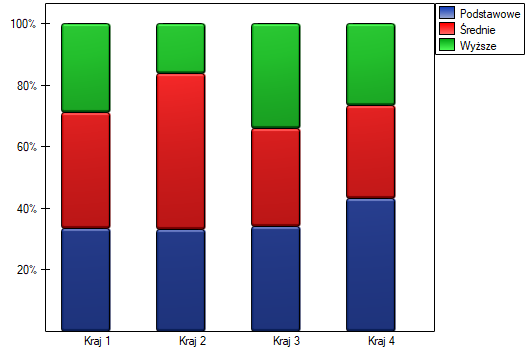
=średnie, 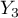 =wyższe). Rozkład danych przedstawia tabela kontyngencji:
=wyższe). Rozkład danych przedstawia tabela kontyngencji:
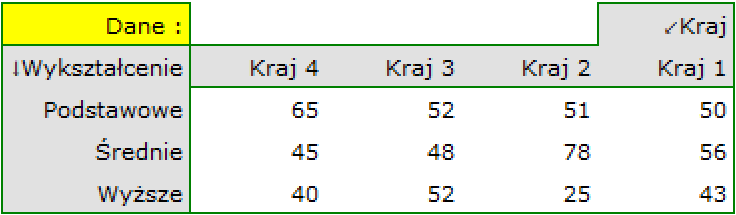
Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy wykształceniem a krajem zamieszkania.
Hipotezy:
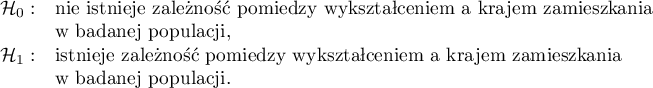
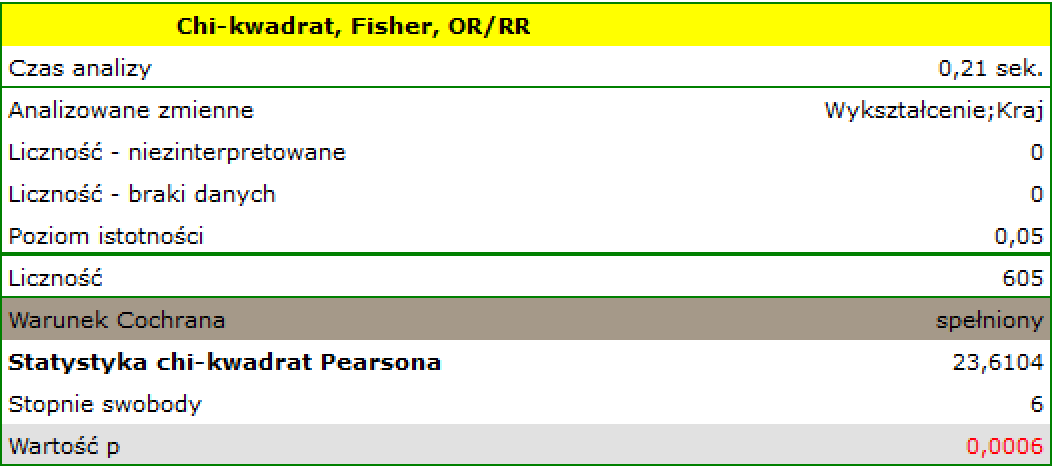
Warunek Cochrana jest spełniony.
Wartość 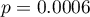 . Zatem na poziomie istotności
. Zatem na poziomie istotności  możemy powiedzieć, że istniej zależność pomiędzy krajem zamieszkania a wykształceniem w badanej populacji.
możemy powiedzieć, że istniej zależność pomiędzy krajem zamieszkania a wykształceniem w badanej populacji.
Jeśli interesują nas dokładniejsze informacje na temat wykrytych zależności, uzyskamy je wyznaczając porównania wielokrotne poprzez opcje Fisher, Yates i inne… a następnie Wielokrotne porównania kolumn (RxC) i jedną z poprawek np. Benjamini-Hochberg
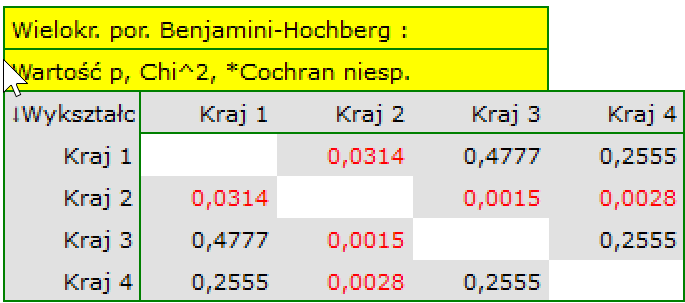
Dokładniejsza analiza pozwala stwierdzić, że jedynie drugi kraj różni się poziomem wykształcenia od pozostałych krajów w sposób istotny statystycznie.
2014/08/22 20:00
Test chi-kwadrat dla małych tabel
Test ten opiera się na danych zebranych w postaci tabeli kontyngencji 2 cech ( ,
,  ), z których każda ma możliwe 2 kategorie
), z których każda ma możliwe 2 kategorie 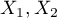 oraz
oraz 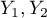 .
.
Okno z ustawieniami opcji testu Chi-kwadrat oraz jego poprawek wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher, OR/RR lub poprzez ''Kreator''.
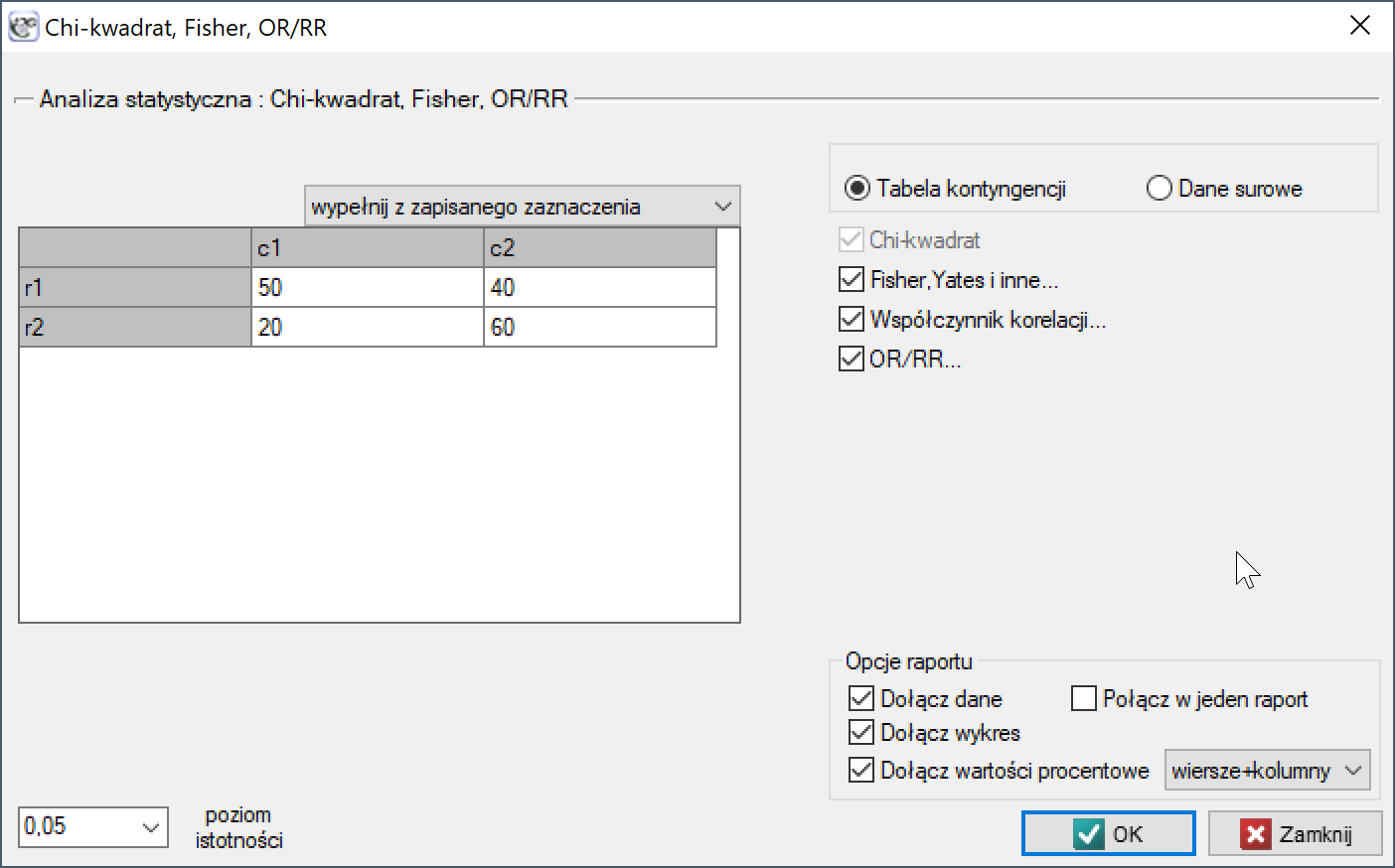
Test  dla tabel
dla tabel 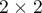 (ang. Pearson's Chi-square test), Karl Pearson 1900. Test ten jest zawężeniem testu chi-kwadrat dla tabel (r x c).
(ang. Pearson's Chi-square test), Karl Pearson 1900. Test ten jest zawężeniem testu chi-kwadrat dla tabel (r x c).
Statystyka testowa ma postać:
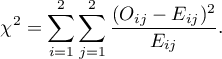
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z jednym stopniem swobody.
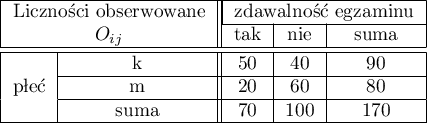
Przykład (plik płeć-egzamin.pqs)
Rozpatrzmy próbę składającą się z 170 osób (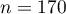 ), dla których badamy 2 cechy (
), dla których badamy 2 cechy ( =płeć,
=płeć,  =zdawalność egzaminu). Każda z tych cech występuje w dwóch kategoriach (
=zdawalność egzaminu). Każda z tych cech występuje w dwóch kategoriach ( =k,
=k,  =m,
=m, 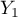 =tak,
=tak, 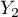 =nie). Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy płcią a zdawalnością egzaminu. Rozkład danych przedstawia tabeli kontyngencji:
=nie). Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy płcią a zdawalnością egzaminu. Rozkład danych przedstawia tabeli kontyngencji:
Hipotezy:
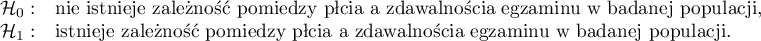
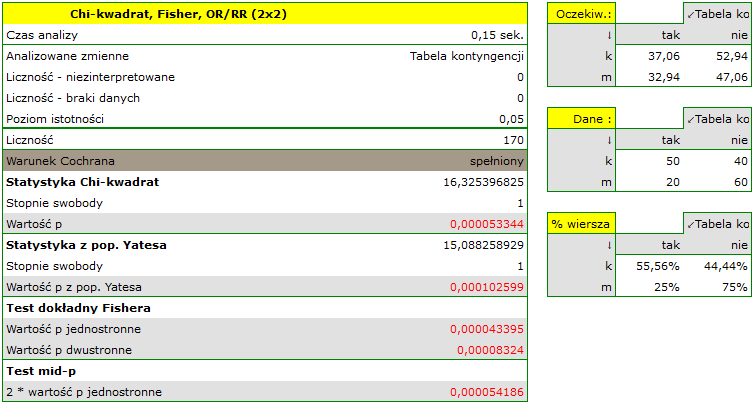
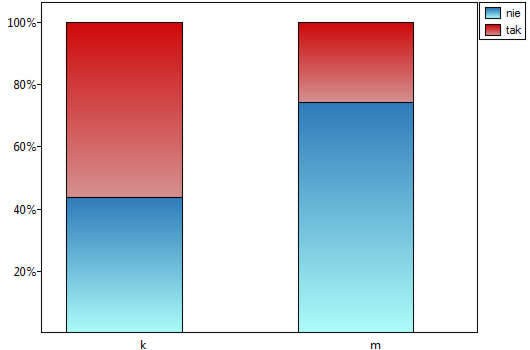
Tabela liczności oczekiwanych nie zawiera wartości mniejszych niż 5. Warunek Cochrana jest spełniony.
Przy przyjętym poziomie istotności  wszystkie wykonane testy potwierdziły prawdziwość hipotezy alternatywnej:
wszystkie wykonane testy potwierdziły prawdziwość hipotezy alternatywnej:
- test chi-kwadrat, wartość
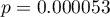 ,
, - test chi-kwadrat z poprawką Yeatesa, wartość
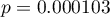 ,
, - test dokładny Fishera, wartość
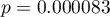 ,
, - test mid-p, wartość
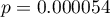
Zatem istnieje zależność pomiędzy płcią a zdawalnością egzaminu w badanej populacji. Istotnie częściej ten egzamin zdają kobiety (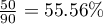 z wszystkich kobiet w próbie zdało egzamin) niż mężczyźni (
z wszystkich kobiet w próbie zdało egzamin) niż mężczyźni (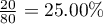 z wszystkich mężczyzn w próbie zdało egzamin)
z wszystkich mężczyzn w próbie zdało egzamin)
2014/08/22 20:00
Test Fishera dla tabel dużych tabel
Test Fishera dla tabel 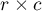 zwany jest również testem Fishera-Freemana-Haltona (ang. Fisher-Freeman-Halton test), Freeman G.H., Halton J.H. (1951)12). Test ten jest rozszerzeniem na tabele
zwany jest również testem Fishera-Freemana-Haltona (ang. Fisher-Freeman-Halton test), Freeman G.H., Halton J.H. (1951)12). Test ten jest rozszerzeniem na tabele 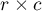 testu dokładnego Fishera. Określa dokładne prawdopodobieństwo wystąpienia konkretnego rozkładu liczb w tabeli przy znanym
testu dokładnego Fishera. Określa dokładne prawdopodobieństwo wystąpienia konkretnego rozkładu liczb w tabeli przy znanym  i ustalonych sumach brzegowych.
i ustalonych sumach brzegowych.
Jeśli sumy brzegowe wierszy zdefiniujemy jako:
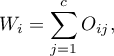
gdzie:
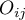
 liczności obserwowane w tabeli kontyngencji,
liczności obserwowane w tabeli kontyngencji,
a sumy brzegowe kolumn jako:
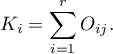
To przy ustalonych sumach brzegowych, dla różnych układów wartości obserwowanych oznaczonych jako 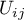 wyznaczamy prawdopodobieństwa
wyznaczamy prawdopodobieństwa 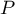 :
:
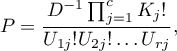
gdzie
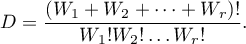
Dokładny poziom istotności  jest sumą tych prawdopodobieństw
jest sumą tych prawdopodobieństw 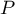 (wyznaczonych dla nowych wartości
(wyznaczonych dla nowych wartości 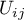 ), które są mniejsze lub równe prawdopodobieństwu
), które są mniejsze lub równe prawdopodobieństwu 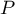 tabeli z wartościami początkowymi
tabeli z wartościami początkowymi 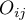
Porównujemy dokładną wartość  z poziomem istotności
z poziomem istotności  :.
:.
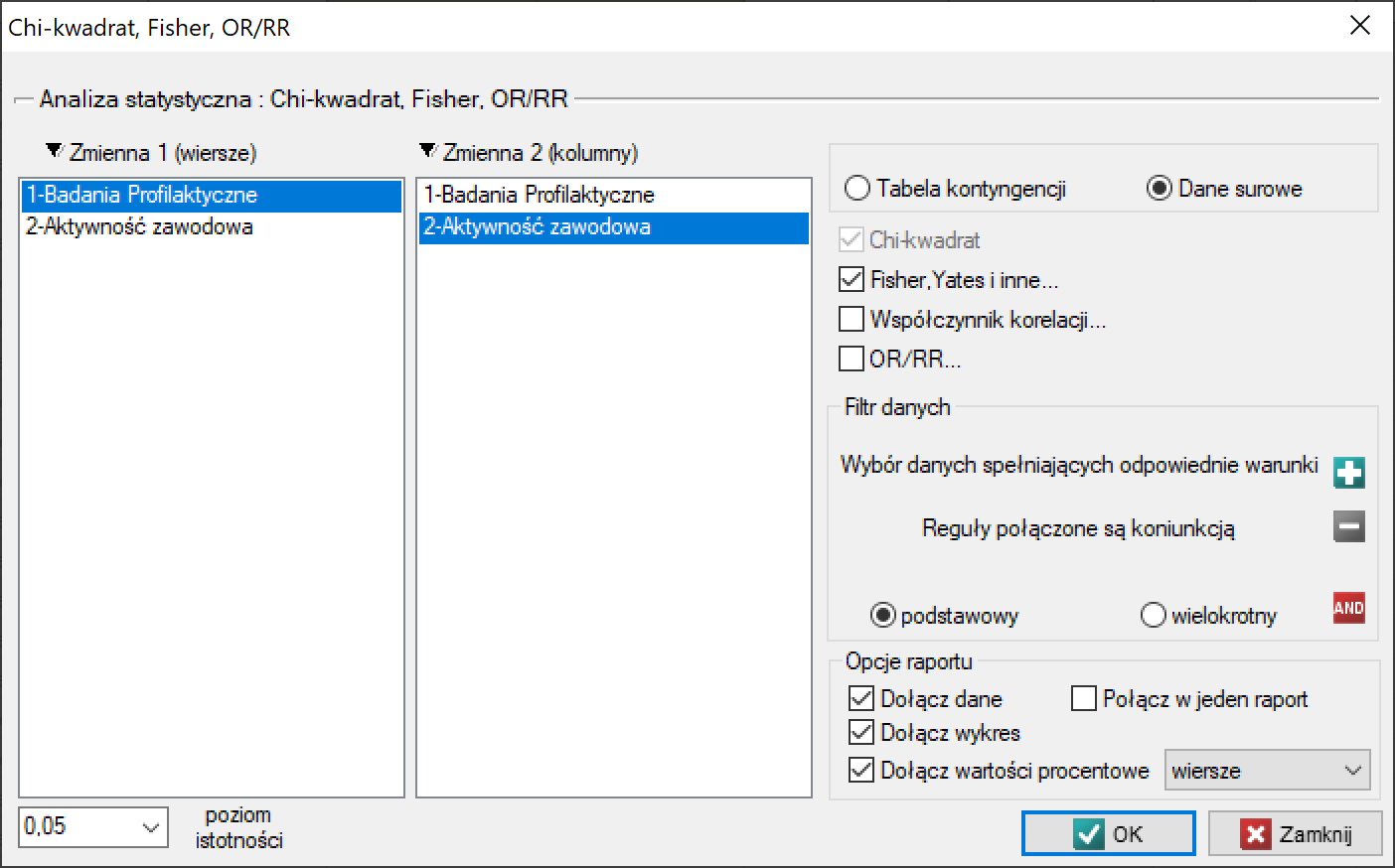
Okno z ustawieniami opcji testu dokładny Fishera (RxC) wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher OR/RR lub poprzez ''Kreator''.
Info.
Procedura obliczania wartości  dla tego testu bazuje na algorytmie opublikowanym w pracy Mehta (1986)13).
dla tego testu bazuje na algorytmie opublikowanym w pracy Mehta (1986)13).
Przykład (plik praca-profilaktyka.pqs)
W populacji osób zamieszkujących na obszarach wiejskich gminy Komorniki badano czy wykonywanie badań profilaktyki zdrowia jest uzależnione od rodzaju aktywność zawodowej mieszkańców. Zebrano losową próbę 120 osób i zapytano o wykształcenie oraz o to czy osoby te wykonują badania profilaktyczne. Pełną odpowiedź uzyskano od 113 osób.
dane_praca_profilaktyka
Hipotezy:

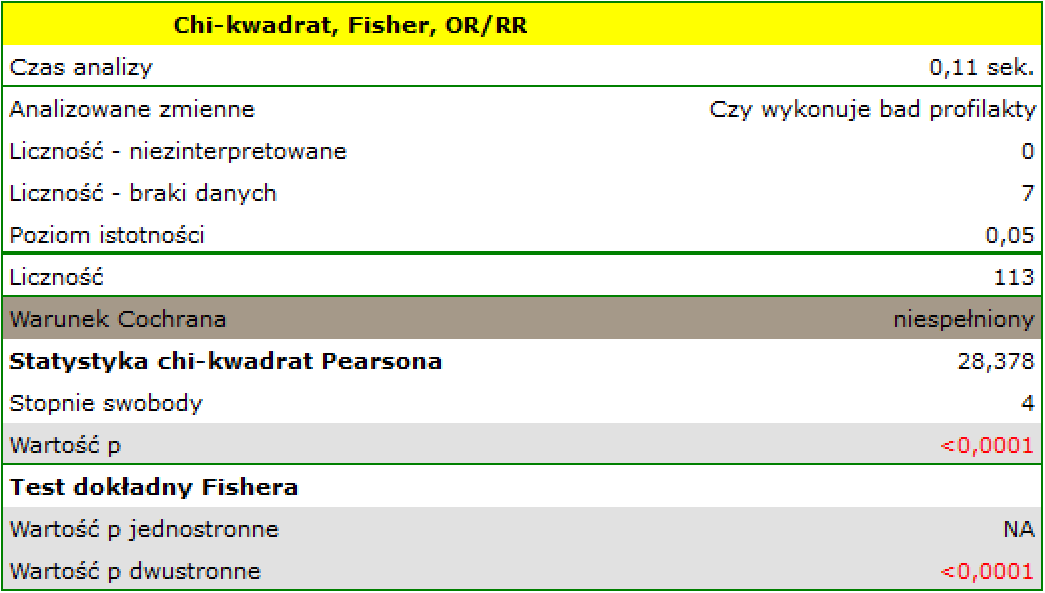
Warunek Cochrana nie jest spełniony, przez co nie powinniśmy stosować testu chi-kwadrat.
Wartość 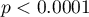 . Zatem na poziomie istotności
. Zatem na poziomie istotności  możemy powiedzieć, że istniej zależność pomiędzy wykonywaniem badań profilaktycznych a rodzajem wykonywanej pracy przez mieszkańców obszarów wiejskich gminy Komorniki.
możemy powiedzieć, że istniej zależność pomiędzy wykonywaniem badań profilaktycznych a rodzajem wykonywanej pracy przez mieszkańców obszarów wiejskich gminy Komorniki.
Jeśli interesują nas dokładniejsze informacje na temat wykrytych zależności, uzyskamy je wyznaczając porównania wielokrotne poprzez opcje Fisher, Yates i inne… a następnie Wielokrotne porównania kolumn (RxC) i jedną z poprawek np. Benjamini-Hochberg
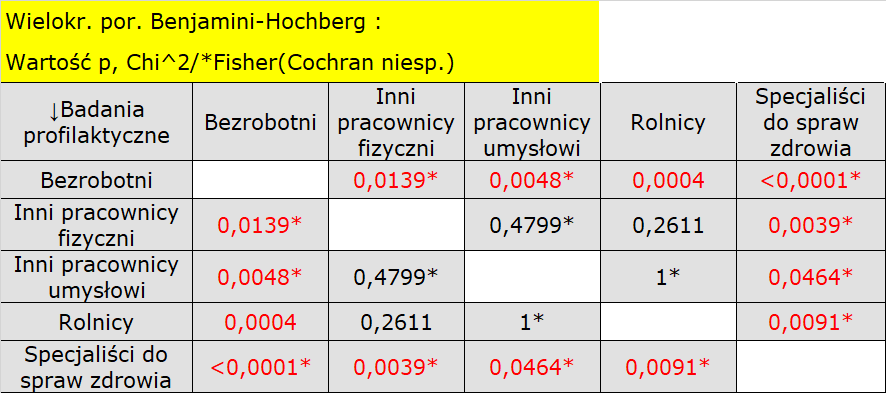
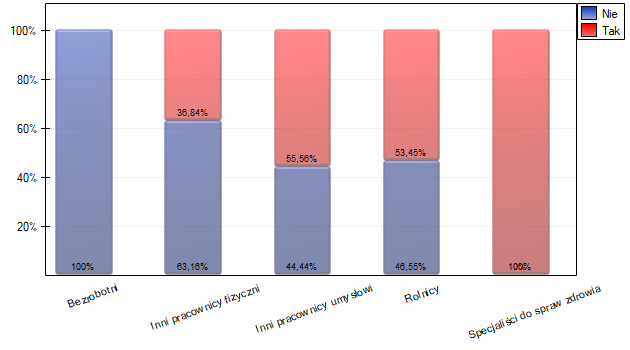
Dokładniejsza analiza pozwala stwierdzić, że specjaliści do spraw zdrowia istotnie częściej niż pozostałe grupy wykonują badania profilaktyczne (100% osób w tej grupie wykonało badania), a bezrobotni istotnie rzadziej (nikt w tej grupie nie wykonał badania). Rolnicy, inni pracownicy fizyczni i inni pracownicy umysłowi w około 50% wykonują badania profilaktyczne co powoduje, że te trzy grupy nie różnią się od siebie istotnie statystycznie. Część wartości p uzyskanych w tabeli oznaczona jest gwiazdką, oznacza ona te wyniki które powstały poprzez użycie testu dokładnego Fishera wraz z poprawką Benjaminiego-Hochberga, wartości nie oznaczone są wynikiem testu chi-kwadrat wraz z poprawką Benjaminiego-Hochberga, przy którym założenia Cochrana były spełnione
2020/10/06 12:50
· admin
Poprawki testu chi-kwadrat dla małych tabel
Testy te opierają się na danych zebranych w postaci tabeli kontyngencji 2 cech ( ,
,  ), z których każda ma możliwe 2 kategorie
), z których każda ma możliwe 2 kategorie 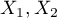 oraz
oraz 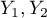 .
.
Test chi-kwadrat z poprawką Yatesa na ciągłość
Test  z poprawką Yatesa (ang. Chi-square test with Yates correction), Frank Yates (1934)14) jest testem bardziej konserwatywny od testu chi-kwadrat (trudniej niż test chi-kwadrat odrzuca hipotezę zerową). Poprawka na ciągłość ma zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu chi-kwadrat.
z poprawką Yatesa (ang. Chi-square test with Yates correction), Frank Yates (1934)14) jest testem bardziej konserwatywny od testu chi-kwadrat (trudniej niż test chi-kwadrat odrzuca hipotezę zerową). Poprawka na ciągłość ma zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu chi-kwadrat.
Statystyka testowa ma postać:
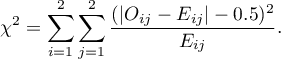
Test Fishera dla tabel 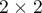 nazywany jest również testem dokładnym Fishera (ang. Fisher exact test), R. A. Fisher (193415), 193516)). Test ten określa dokładne prawdopodobieństwo wystąpienia konkretnego rozkładu liczb w tabeli przy znanym
nazywany jest również testem dokładnym Fishera (ang. Fisher exact test), R. A. Fisher (193415), 193516)). Test ten określa dokładne prawdopodobieństwo wystąpienia konkretnego rozkładu liczb w tabeli przy znanym  i ustalonych sumach brzegowych.
i ustalonych sumach brzegowych.
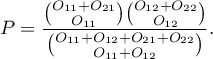 Przy znanych sumach brzegowych, dla różnych układów wartości obserwowanych wyznaczamy prawdopodobieństwa
Przy znanych sumach brzegowych, dla różnych układów wartości obserwowanych wyznaczamy prawdopodobieństwa 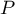 . Dokładny poziom istotności
. Dokładny poziom istotności  jest sumą tych prawdopodobieństw, które są mniejsze lub równe badanemu prawdopodobieństwu.
jest sumą tych prawdopodobieństw, które są mniejsze lub równe badanemu prawdopodobieństwu.
mid-p jest korektą testu dokładnego Fishera. Ta zmodyfikowana wartość  jest rekomendowana przez wielu statystyków (Lancaster 196117), Anscombe 198118), Pratt i Gibbons 198119), Plackett 198420), Miettinen 198521) i Barnard 198922), Rothman 200823)) jako metoda zmniejszenia konserwatyzm testu dokładnego Fishera. W rezultacie testem mid-p szybciej odrzucimy hipotezę zerowa niż dokładnym testem Fishera. Dla dużych prób wartość
jest rekomendowana przez wielu statystyków (Lancaster 196117), Anscombe 198118), Pratt i Gibbons 198119), Plackett 198420), Miettinen 198521) i Barnard 198922), Rothman 200823)) jako metoda zmniejszenia konserwatyzm testu dokładnego Fishera. W rezultacie testem mid-p szybciej odrzucimy hipotezę zerowa niż dokładnym testem Fishera. Dla dużych prób wartość  otrzymana przy pomocy testu
otrzymana przy pomocy testu  z poprawką Yatesa i test Fishera dają zbliżone wyniki, natomiast wartość
z poprawką Yatesa i test Fishera dają zbliżone wyniki, natomiast wartość  testu
testu  bez korekcji koresponduje z wartością mid-p.
bez korekcji koresponduje z wartością mid-p.
Wartość  mid-p wyznaczana jest przez przekształcenie wartości prawdopodobieństwa dla testu dokładnego Fishera. Jednostronna wartość
mid-p wyznaczana jest przez przekształcenie wartości prawdopodobieństwa dla testu dokładnego Fishera. Jednostronna wartość  wyznaczana jest ze wzoru:
wyznaczana jest ze wzoru:
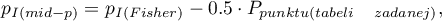
gdzie:
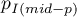
 wartość jednostronna
wartość jednostronna  testu mid-p
testu mid-p
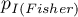
 wartość jednostronna
wartość jednostronna  testu dokładnego Fishera
testu dokładnego Fishera
a dwustronna wartość  jest definiowana jako podwojona wartość mniejszego z jednostronnych prawdopodobieństw:
jest definiowana jako podwojona wartość mniejszego z jednostronnych prawdopodobieństw:
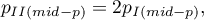
gdzie:
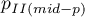
 wartość dwustronna
wartość dwustronna  testu mid-p.
testu mid-p.
2020/10/06 13:39
· admin
Test chi-kwadrat dla trendu
Test  dla trendu nazywany również testem dla trendu Cochrana-Armitage (ang. Cochran-Armitage test for trend)24)25) służy do weryfikacji hipotezy o istnieniu trendu w proporcjach dla poszczególnych kategorii badanej zmiennej (cechy). Opiera się na danych zebranych w postaci tabeli kontyngencji 2 cech, z których pierwsza ma możliwe
dla trendu nazywany również testem dla trendu Cochrana-Armitage (ang. Cochran-Armitage test for trend)24)25) służy do weryfikacji hipotezy o istnieniu trendu w proporcjach dla poszczególnych kategorii badanej zmiennej (cechy). Opiera się na danych zebranych w postaci tabeli kontyngencji 2 cech, z których pierwsza ma możliwe  uporządkowanych kategorii:
uporządkowanych kategorii: 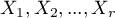 a druga 2 kategorie
a druga 2 kategorie 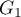 ,
, 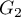 .
.
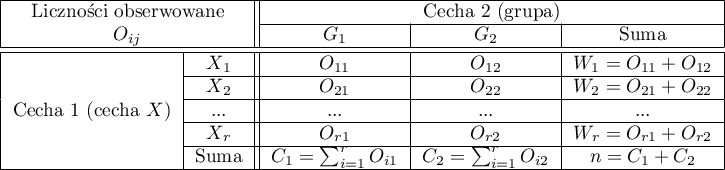
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
- model niezależny (druga cecha, to 2 niezależne grupy).
Niech 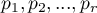 oznaczają proporcje
oznaczają proporcje 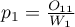 ,
, 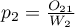 ,…,
,…, 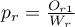 .
.
Hipotezy:
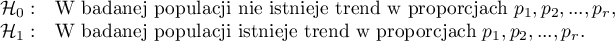
Statystyka testowa ma postać:
![LaTeX \begin{displaymath}
\chi^2=\frac{\left[\left(\sum_{i=1}^r i\cdot O_{i1}\right) -C_1\left(\sum_{i=1}^r\frac{i\cdot W_i}{n}\right)\right]^2}{\frac{C_1}{n}\left(1-\frac{C_1}{n}\right)\left[\left(\sum_{i=1}^n i^2 W_i\right)-n\left(\sum_{i=1}^n\frac{i \cdot W_i}{n}\right)^2\right]}.
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/imgd32bd126527cf05771f082e9a0735129.png)
Statystyk ta ma rozkład chi-kwadrat z 1 stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności poziomem istotności
porównujemy z poziomem istotności poziomem istotności  :
:

Okno z ustawieniami opcji testu Chi-kwadrat dla trendu wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher, OR/RR, opcja Fisher, Yates i inne…→Chi-kwadrat dla trendu.
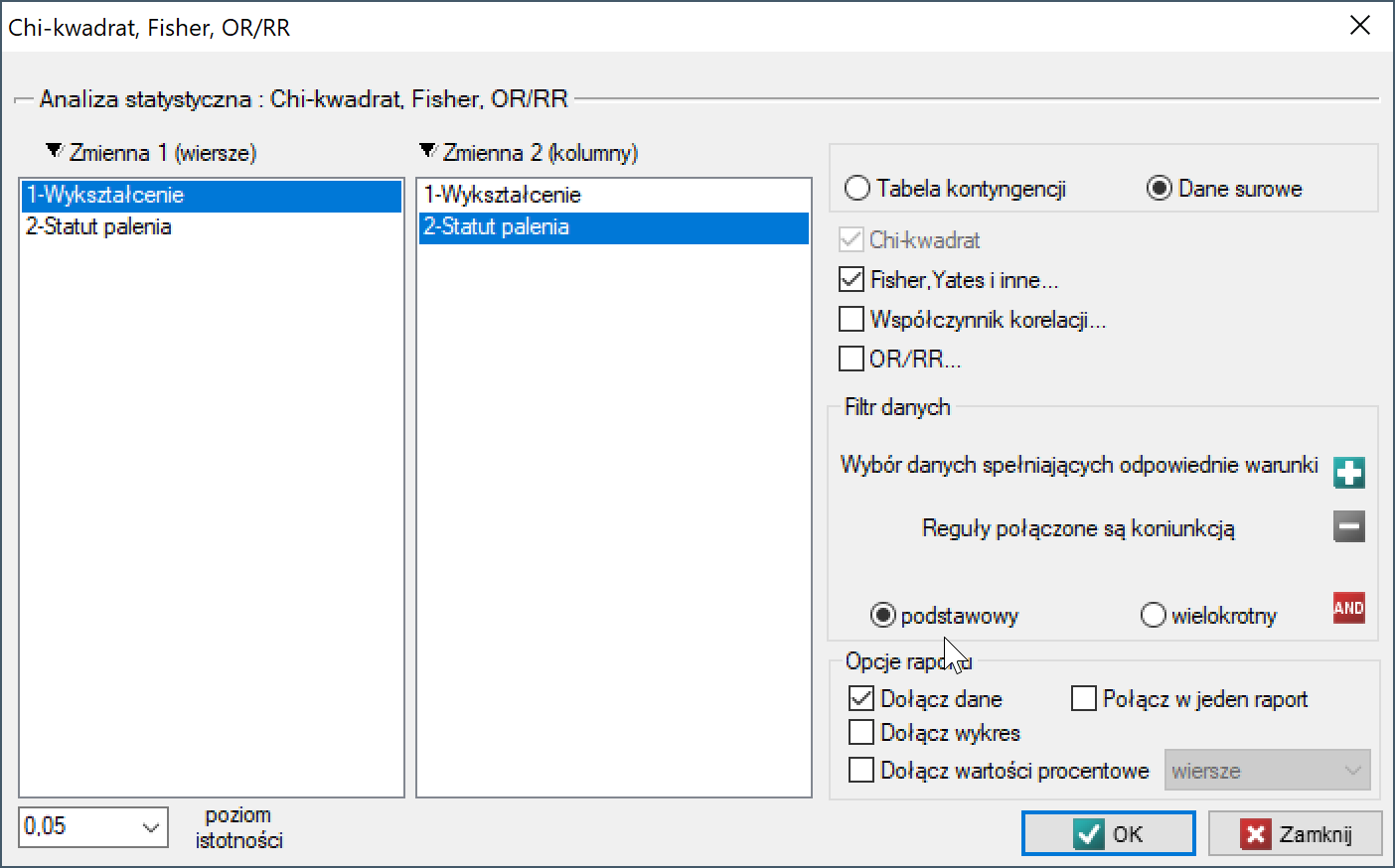
Przykład (palenie-wykształcenie.pqs)
Sprawdzamy czy palenie papierosów związane jest z wykształceniem mieszkańców pewnej wsi. Wylosowano próbę 122 osób. Dane zapisano w pliku.
Zakładamy, że zależność może być dwojakiego typu tzn. czym bardziej wykształceni ludzie, tym częściej palą lub czym bardziej wykształceni ludzie, tym rzadziej palą. Poszukujemy zatem rosnącego lub malejącego trendu.
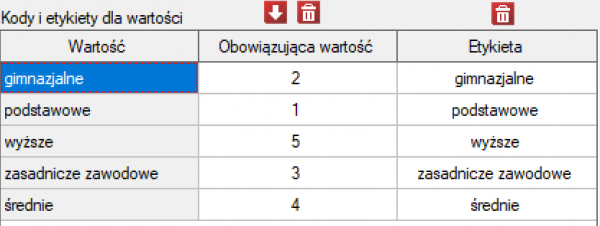
Przed przystąpieniem do analizy musimy przygotować dane, tzn. musimy wskazać kolejność w jakiej mają się pojawiać kategorie wykształcenia. W tym celu z właściwości zmiennej Wykształcenie wybieramy Kody/Etykiety/Format… i nadajemy kolejność podając kolejne liczby naturalne. Przypisujemy również etykiety.
Hipotezy:


Wartość 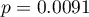 , co w porównaniu z poziomem istotności
, co w porównaniu z poziomem istotności  =0.05 świadczy o prawdziwości hipotezy alternatywnej mówiącej o występowaniu trendu.
=0.05 świadczy o prawdziwości hipotezy alternatywnej mówiącej o występowaniu trendu.
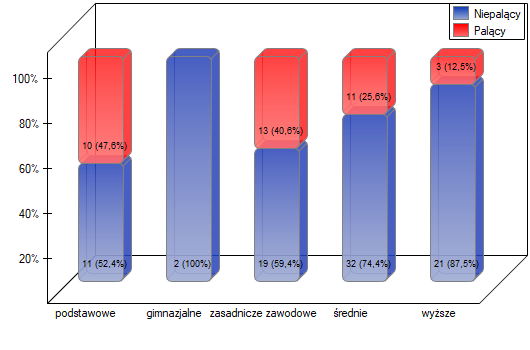
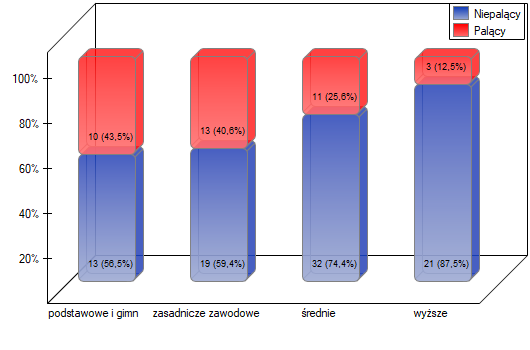
Jak wynika z wykresu czym osoby są bardziej wykształcone, tym rzadziej palą. Jednak wynik uzyskany przez osoby o wykształceniu gimnazjalnym odbiega od tego trendu. Ponieważ wykształcenie gimnazjalne dotyczy tylko dwóch osób, nie miało to dużego wpływu na rysujący się trend. Ze względu na bardzo małą liczność tej grupy postanowiono analizę powtórzyć dla połączonych kategorii wykształcenia podstawowego i gimnazjalnego.
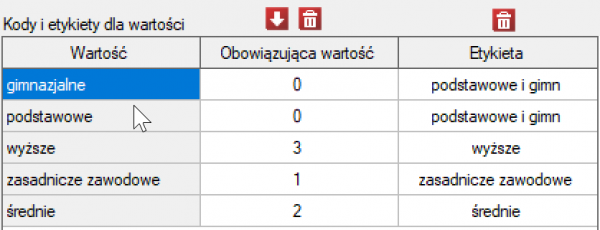
Uzyskano ponownie niewielką wartość 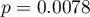 i potwierdzenie istotnego statystycznie trendu.
i potwierdzenie istotnego statystycznie trendu.
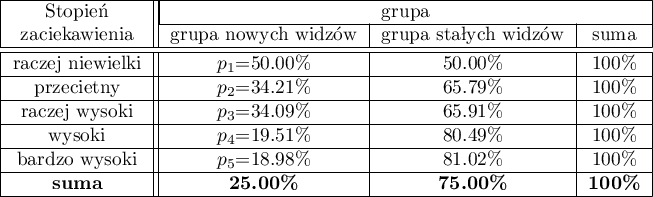
Z powodu spadku oglądalności pewnego serialu telewizyjnego przeprowadzono badanie opinii widzów tego serialu. W tym celu przepytano 100 osób, które rozpoczęły oglądanie serialu w ostatnim czasie i 300, które oglądają systematycznie serial od początku. Zapytano ich między innymi o ocenę stopnia zaabsorbowania widza losami bohaterów. Wyniki zapisano w tabeli poniżej:
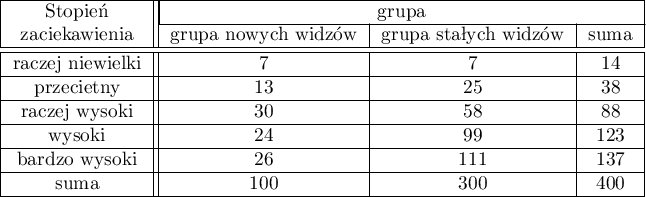
Nowi widzowie stanowią 25% badanych. Taka proporcja nie utrzymuje się jednak dla każdej kategorii „stopnia zaciekawienia” ale przedstawia się następująco:
Hipotezy:
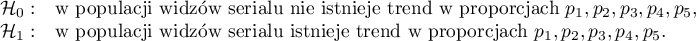
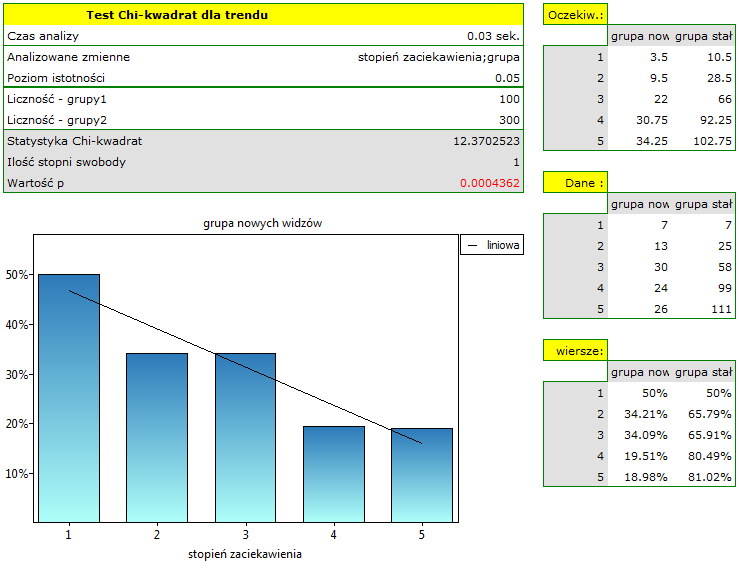
Wartość 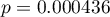 , co w porównaniu z poziomem istotności
, co w porównaniu z poziomem istotności  =0.05 świadczy o prawdziwości hipotezy alternatywnej mówiącej o występowaniu trendu w proporcjach
=0.05 świadczy o prawdziwości hipotezy alternatywnej mówiącej o występowaniu trendu w proporcjach 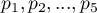 . Jak wynika z tabeli kontyngencji wartości procentowych wyliczanych z sumy kolumn, jest to trend malejący (im grupa widzów jest bardziej zainteresowana losami bohaterów serialu, tym mniejszą jej część stanowią nowi widzowie).
. Jak wynika z tabeli kontyngencji wartości procentowych wyliczanych z sumy kolumn, jest to trend malejący (im grupa widzów jest bardziej zainteresowana losami bohaterów serialu, tym mniejszą jej część stanowią nowi widzowie).
2014/08/22 20:00
Test Z dla dwóch niezależnych proporcji
Test  dla dwóch niezależnych proporcji stosujemy w podobnych sytuacjach jak test chi-kwadrat (2x2), tzn. gdy mamy 2 niezależne próby o liczności
dla dwóch niezależnych proporcji stosujemy w podobnych sytuacjach jak test chi-kwadrat (2x2), tzn. gdy mamy 2 niezależne próby o liczności 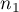 i
i 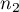 , w których możemy uzyskać 2 możliwe wyniki badanej cechy (jeden z nich to wynik wyróżniony o liczności
, w których możemy uzyskać 2 możliwe wyniki badanej cechy (jeden z nich to wynik wyróżniony o liczności 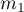 - w pierwszej próbie i
- w pierwszej próbie i 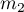 - w drugiej próbie). Dla prób tych możemy również wyznaczyć wyróżnione proporcje
- w drugiej próbie). Dla prób tych możemy również wyznaczyć wyróżnione proporcje 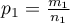 i
i 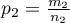 . Test ten służy do weryfikacji hipotezy, że wyróżnione proporcje
. Test ten służy do weryfikacji hipotezy, że wyróżnione proporcje 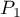 i
i 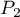 w populacjach, z których pochodzą próby są sobie równe.
w populacjach, z których pochodzą próby są sobie równe.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
- duża liczność.
Hipotezy:
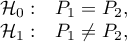
gdzie:
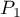 ,
, 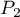 frakcja dla pierwszej i drugiej populacji.
frakcja dla pierwszej i drugiej populacji.
Statystyka testowa ma postać:
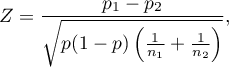
gdzie:
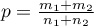 .
.
Zmodyfikowana o poprawkę na ciągłość statystyka testowa ma postać:
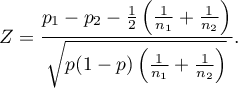
Statystyka bez korekcji na ciągłość jak i z tą korekcją ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

W programie oprócz różnicy proporcji wyliczana jest wartość wskaźnika NNT i/lub NNH.
NNT (ang. number needed to treat)  wskaźnik stosowany w medycynie, oznacza liczbę pacjentów, których trzeba poddać leczeniu przez określony czas, aby wyleczyć jedną osobę, która w innych okolicznościach nie wyzdrowiałaby. NNT wyliczane jest z wzoru:
wskaźnik stosowany w medycynie, oznacza liczbę pacjentów, których trzeba poddać leczeniu przez określony czas, aby wyleczyć jedną osobę, która w innych okolicznościach nie wyzdrowiałaby. NNT wyliczane jest z wzoru:
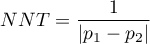
i jest cytowane wtedy, gdy różnica 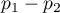 jest dodatnia.
jest dodatnia.
NNH (ang. number needed to harm)  wskaźnik stosowany w medycynie, oznacza liczbę pacjentów, których narażenie na ryzyko przez określony czas, powoduje uszczerbek na zdrowiu u jednej osoby, która w innych okolicznościach nie doznałaby uszczerbku. NNH wyliczane jest w ten sam sposób co NNT, ale jest cytowane wtedy, gdy różnica
wskaźnik stosowany w medycynie, oznacza liczbę pacjentów, których narażenie na ryzyko przez określony czas, powoduje uszczerbek na zdrowiu u jednej osoby, która w innych okolicznościach nie doznałaby uszczerbku. NNH wyliczane jest w ten sam sposób co NNT, ale jest cytowane wtedy, gdy różnica 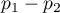 jest ujemna.
jest ujemna.
Przedział ufności  im węższy przedział ufności, tym bardziej precyzyjne oszacowanie. Jeśli w przedziale ufności zawarte jest 0 dla różnicy ryzyka, a
im węższy przedział ufności, tym bardziej precyzyjne oszacowanie. Jeśli w przedziale ufności zawarte jest 0 dla różnicy ryzyka, a 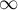 dla NNT i/lub NNH, to jest wskazanie do tego, by dany wynik traktować jako nieistotny statystycznie.
dla NNT i/lub NNH, to jest wskazanie do tego, by dany wynik traktować jako nieistotny statystycznie.
Uwaga!
Przedziały ufności dla różnicy dwóch niezależnych proporcji od wersji PQStat 1.3.0 estymowane są w oparciu o metodę Newcomba-Wilsona (Bender (2001)26), Newcombe (1998)27), Wilson (1927)28)). W poprzednich wersjach były estymowane w oparciu o metodę Walda.
Uzasadnienie zmiany:
Przedziały ufności oparte o klasyczną metodę Walda są odpowiednie dla dużych rozmiarów próbek i różnicy proporcji dalekiej od 0 lub 1. Dla małych prób i różnicy proporcji bliskiej tym skrajnym wartościom, w wielu sytuacjach praktycznych, metoda Walda może prowadzić do wyników niewiarygodnych (Newcombe 199829), Miettinen 198530), Beal 198731), Wallenstein 199732)). Porównanie i przeanalizowanie wielu metod, które mogą być używane zamiast prostej metody Walda, można znaleźć w pracy Newcombe (1998)33). Sugerowaną, odpowiednią również dla skrajnych wartości proporcji, jest roszerzona na przedziały dla różnicy dwóch niezależnych proporcji, metoda opublikowana po raz pierwszy przez Wilsona (1927)34).
Uwaga!
Przedział ufności dla NNT i/lub NNH wyliczany jest jako odwrotność przedziału dla proporcji, zgodnie ze sposobem zaproponowanym przez Altmana (Altman (1998)35)).
Okno z ustawieniami opcji testu Z dla dwóch niezależnych proporcji wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Z dla dwóch niezależnych proporcji.
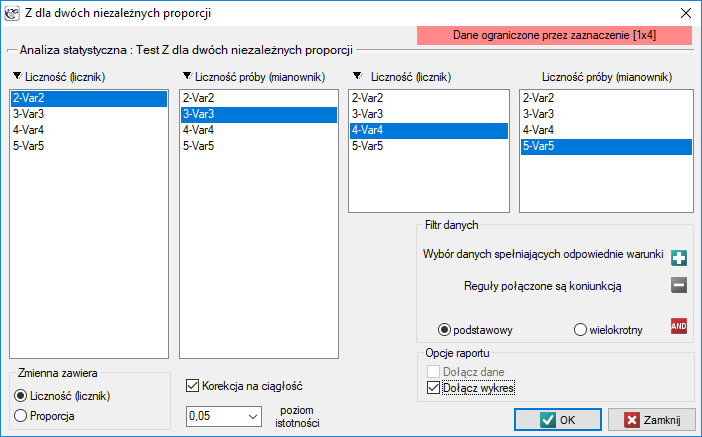
Przykład c.d. (plik płeć-egzamin.pqs)
Wiemy, że 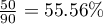 z wszystkich kobiet w próbie zdaje pozytywnie egzamin i
z wszystkich kobiet w próbie zdaje pozytywnie egzamin i 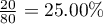 z wszystkich mężczyzn w próbie zdaje egzamin pozytywnie.
Dane możemy zapisać na dwa sposoby
z wszystkich mężczyzn w próbie zdaje egzamin pozytywnie.
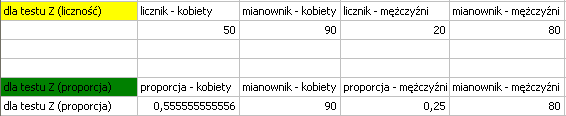
Dane możemy zapisać na dwa sposoby  jako licznik i mianownik dla każdej próby, lub jako proporcja i mianownik dla każdej próby:
jako licznik i mianownik dla każdej próby, lub jako proporcja i mianownik dla każdej próby:
Hipotezy:
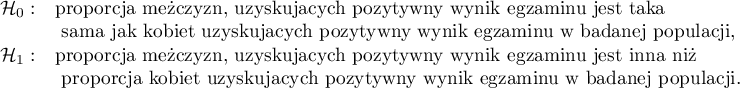
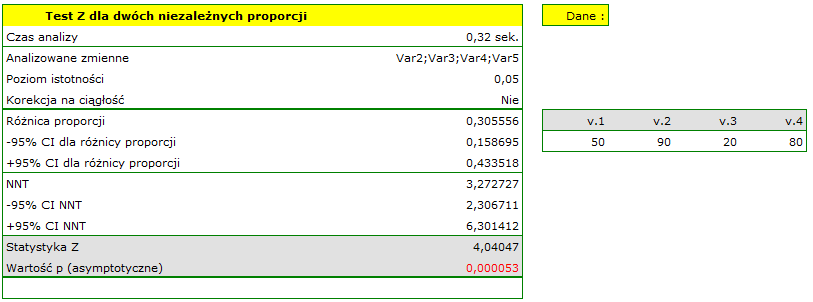
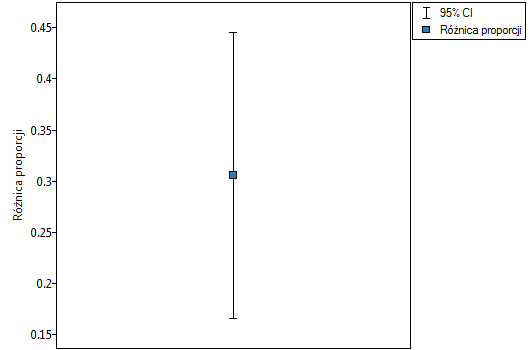
Uwaga!
Ponieważ w arkuszu danych znajduje się więcej informacji, przed rozpoczęciem analizy należy zaznaczyć odpowiedni obszar (dane bez nagłówków). W oknie testu natomiast wybrać opcję mówiącą o zawartości zmiennej (liczność (licznik) lub proporcja).
Różnica proporcji wyróżnionych w próbie to 30.56%, a 95% przedział ufności dla niej (15.90%, 43.35%) nie zawiera 0.
Na podstawie testu  bez poprawki na ciągłość (
bez poprawki na ciągłość ( =0.000053) jak też z poprawką na ciągłość (
=0.000053) jak też z poprawką na ciągłość ( =0.0001), na poziomie istotności
=0.0001), na poziomie istotności  =0.05 (podobnie jak w przypadku testu dokładnego Fishera, jego poprawki mid-p, testu
=0.05 (podobnie jak w przypadku testu dokładnego Fishera, jego poprawki mid-p, testu  i testu
i testu  z poprawką Yatesa) przyjmujemy hipotezę alternatywną. Zatem proporcja mężczyzn, uzyskujących pozytywny wynik egzaminu jest inna niż proporcja kobiet uzyskujących pozytywny wynik egzaminu w badanej populacji. Istotnie częściej ten egzamin zdają kobiety (
z poprawką Yatesa) przyjmujemy hipotezę alternatywną. Zatem proporcja mężczyzn, uzyskujących pozytywny wynik egzaminu jest inna niż proporcja kobiet uzyskujących pozytywny wynik egzaminu w badanej populacji. Istotnie częściej ten egzamin zdają kobiety (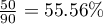 z wszystkich kobiet w próbie zdało egzamin) niż mężczyźni (
z wszystkich kobiet w próbie zdało egzamin) niż mężczyźni (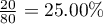 z wszystkich mężczyzn w próbie zdało egzamin).
z wszystkich mężczyzn w próbie zdało egzamin).
Przykład
Załóżmy, że choroba ma śmiertelność 100% bez leczenia, a terapia zmniejsza śmiertelność do 50% - jest to wynik 20 letnich badań. Chcemy wiedzieć jak wiele osób będzie trzeba leczyć, aby zapobiec w ciągu 20 lat 1 śmierci. By odpowiedzieć na to pytanie pobrano dwie 100 osobowe próby z populacji osób chorych. W próbie nieleczonych mamy 100 chorych pacjentów, wiemy, że bez leczenia wszyscy oni umrą. W próbie leczonych mamy również 100 pacjentów, z których 50 przeżyje.

Wyliczymy wskaźnik NNT.
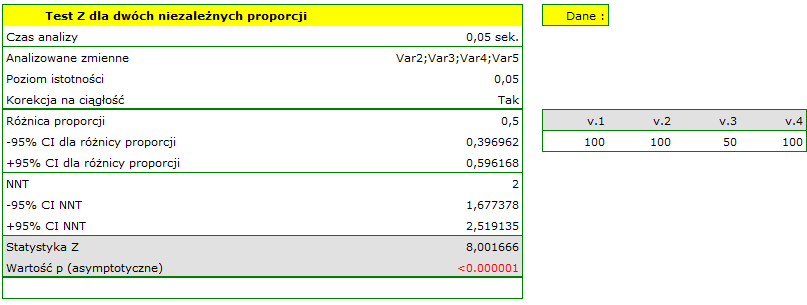
Różnica pomiędzy proporcjami jest istotna statystycznie (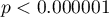 ), ale nas interesuje wskaźnik NNT - wynosi on 2, czyli stosowanie leczenia u 2 chorych przez 20 lat zapobiegnie 1 śmierci. Wyliczony 95% przedział ufności należy zaokrąglić do wartości całkowitych, co daje NNT od 2 do 3 chorych.
), ale nas interesuje wskaźnik NNT - wynosi on 2, czyli stosowanie leczenia u 2 chorych przez 20 lat zapobiegnie 1 śmierci. Wyliczony 95% przedział ufności należy zaokrąglić do wartości całkowitych, co daje NNT od 2 do 3 chorych.
Przykład
Wartość pewnej różnicy proporcji w badaniu porównującym skuteczność leku 1 vs lek 2 wynosiła różnica(95%CI)=-0.08 (-0.27 do 0.11). Ta ujemna różnica proporcji sugeruje, że lek 1 był mniej skuteczny niż lek 2, jego zastosowanie naraziło więc chorych na ryzyko. Ponieważ różnica proporcji jest ujemna, to wyznaczoną odwrotność nazywamy NNH, a ponieważ przedział ufności zawiera nieskończoność NNH(95%CI)= 2.5 (NNH 3.7 to ∞ to NNT 9.1) i przechodzi z NNH do NNT, należy uznać że uzyskany wynik nie jest istotny statystycznie (Altman (1998)36)).
2014/08/22 20:00
Test Z dla dwóch zależnych proporcji
Test  dla dwóch zależnych proporcji stosujemy w podobnych sytuacjach jak test Test McNemara, tzn. gdy mamy 2 zależne grupy pomiarów (
dla dwóch zależnych proporcji stosujemy w podobnych sytuacjach jak test Test McNemara, tzn. gdy mamy 2 zależne grupy pomiarów (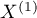 i
i 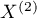 ), w których możemy uzyskać 2 możliwe wyniki badanej cechy (
), w których możemy uzyskać 2 możliwe wyniki badanej cechy ( 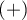 i
i 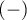 ).
).

Dla grup tych możemy również wyliczyć wyróżnione proporcje 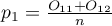 i
i 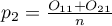 . Test ten służy do weryfikacji hipotezy, że wyróżnione proporcje
. Test ten służy do weryfikacji hipotezy, że wyróżnione proporcje 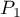 i
i 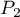 w populacji, z której pochodzi próba są sobie równe.
w populacji, z której pochodzi próba są sobie równe.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
- duża liczność.
Hipotezy:
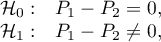
gdzie:
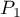 ,
, 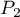 frakcja dla pierwszego i drugiego pomiaru.
frakcja dla pierwszego i drugiego pomiaru.
Statystyka testowa ma postać:
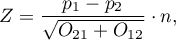
Statystyka Z ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Przedział ufności dla różnicy dwóch zależnych proporcji estymowany jest w oparciu o metodę Newcomba-Wilsona.
Okno z ustawieniami opcji testu Z dla dwóch zależnych proporcji wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Z dla dwóch zależnych proporcji.
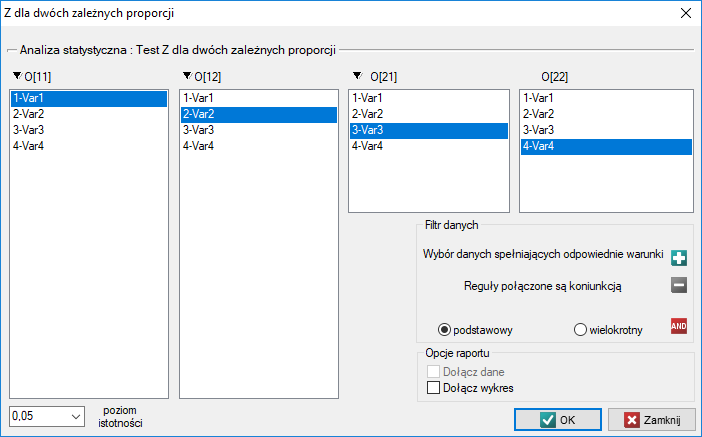
Przykład c.d. (plik opinia.pqs)
Gdy ograniczymy nasze badanie do osób mających zdefiniowany pogląd na temat wykładowcy (tzn. oceniają tylko pozytywnie lub negatywnie), to takich studentów uzyskamy 152. Dane do obliczeń to:  ,
, 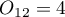 ,
,  ,
, 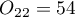 . Wiemy, że
. Wiemy, że 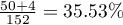 studentów przed egzaminem wyrażało negatywną opinię. Po egzaminie odpowiedni procent wynosił
studentów przed egzaminem wyrażało negatywną opinię. Po egzaminie odpowiedni procent wynosił 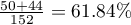 .
.
Hipotezy:

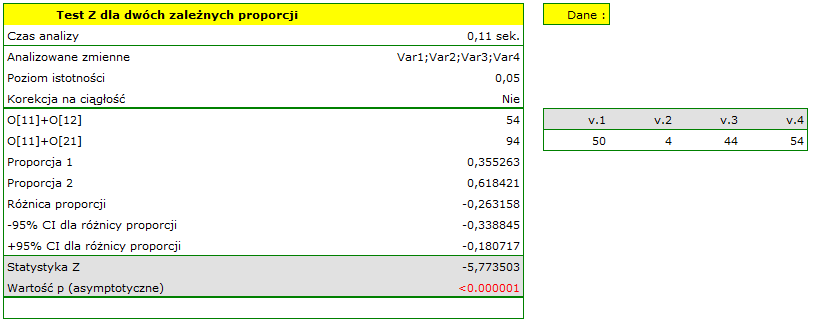
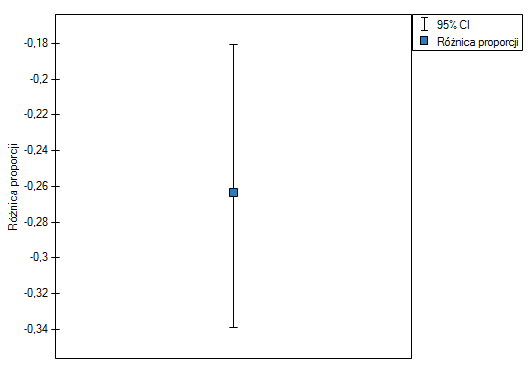
Różnica proporcji wyróżnionych w próbie to 26.32%, a 95% przedział ufności dla niej (18.07%, 33.88%) nie zawiera 0.
Na podstawie testu  (
( =0.0001), na poziomie istotności
=0.0001), na poziomie istotności  =0.05 (podobnie jak w przypadku testu McNemara) przyjmujemy hipotezę alternatywną. Zatem proporcja negatywnych ocen przed egzaminem jest inna niż proporcja negatywnych ocen po egzaminie. Po egzaminie istotnie częściej wykładowca jest oceniany negatywnie.
=0.05 (podobnie jak w przypadku testu McNemara) przyjmujemy hipotezę alternatywną. Zatem proporcja negatywnych ocen przed egzaminem jest inna niż proporcja negatywnych ocen po egzaminie. Po egzaminie istotnie częściej wykładowca jest oceniany negatywnie.
2014/08/22 20:00
Test McNemara, test wewnętrznej symetrii Bowkera
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
Test McNemara (ang. McNemar test), NcNemar (1947)37). Test ten służy do weryfikacji hipotezy o zgodności pomiędzy wynikami dwukrotnych pomiarów 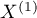 i
i 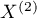 cechy
cechy  (pomiędzy dwiema zmiennymi zależnymi
(pomiędzy dwiema zmiennymi zależnymi 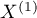 i
i 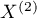 ). Badana cecha może mieć tylko 2 kategorie (oznaczone przez nas
). Badana cecha może mieć tylko 2 kategorie (oznaczone przez nas 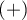 i
i 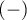 ). Test McNemara można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach
). Test McNemara można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach 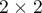 .
.

Hipotezy:
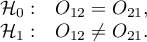
Statystyka testowa ma postać:
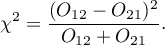
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z jednym stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Poprawka na ciągłość testu McNemara
Poprawka ta jest testem bardziej konserwatywny od testu McNemara (trudniej niż test McNemara odrzuca hipotezę zerową). Ma ona zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu  . Część źródeł podaje, że poprawkę na ciągłość powinno się wykonywać zawsze, natomiast część uznaje, że tylko wtedy, gdy liczności w tabeli są małe.
. Część źródeł podaje, że poprawkę na ciągłość powinno się wykonywać zawsze, natomiast część uznaje, że tylko wtedy, gdy liczności w tabeli są małe.
Statystyka testowa testu McNemara z poprawką na ciągłość ma postać:
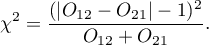
Dokładny test McNemara
Powszechną, ogólną zasadą ważności asymptotycznego testu McNemara chi-kwadrat jest warunek Rufibach, czyli to, że liczba niezgodnych par jest większa niż 10: 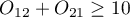 38), gdy warunek ten nie jest spełniony, wówczas powinniśmy bazować na dokładnych wartościach prawdopodobieństwa tego testu 39). Dokładna wartość prawdopodobieństwa testu oparta jest o rozkład dwumianowy i jest testem konserwatywnym, dlatego obok dokładnej wartości testu MnNemara podano również polecaną wartość dokładną mid-p testu McNemara.
38), gdy warunek ten nie jest spełniony, wówczas powinniśmy bazować na dokładnych wartościach prawdopodobieństwa tego testu 39). Dokładna wartość prawdopodobieństwa testu oparta jest o rozkład dwumianowy i jest testem konserwatywnym, dlatego obok dokładnej wartości testu MnNemara podano również polecaną wartość dokładną mid-p testu McNemara.
Jeśli przeprowadzone zostało 2 krotnie badanie tej samej cechy na tych samych obiektach - wówczas dla takiej tabeli wylicza się iloraz szans na zmianę wyniku (z 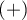 na
na 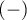 i odwrotnie).
i odwrotnie).
Szansa zmiany wyniku z 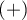 na
na 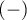 wynosi
wynosi 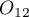 , a szansa zmiany wyniku z
, a szansa zmiany wyniku z 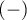 na
na 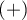 wynosi
wynosi 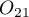 .
.
Iloraz szans (ang. odds ratio - OR) to:
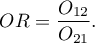
Przedział ufności dla ilorazu szans buduje się w oparciu o błąd standardowy:
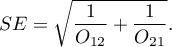
Uwaga!
Dodatkowo, dla prób o niewielkich licznościach, można wyznaczyć dokładny zakres przedziału ufności dla Ilorazu Szans 40).
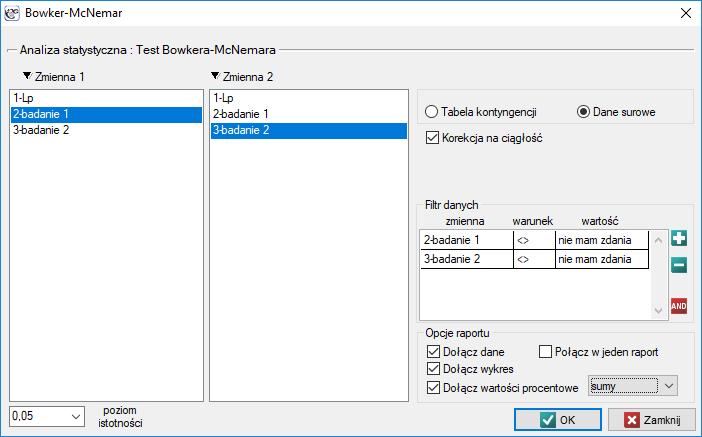
Okno z ustawieniami opcji testu Bowkera-McNemara wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Bowker-McNemar lub poprzez ''Kreator''.
Test wewnętrznej symetrii Bowkera
Test wewnętrznej symetrii Bowkera (ang. Bowker test of internal symmetry), Bowker (1948)41). Test ten jest rozszerzeniem testu McNemara na 2 zmienne o więcej niż dwóch kategoriach (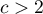 ). Służy do weryfikacji hipotezy o symetryczności wyników dwukrotnych pomiarów
). Służy do weryfikacji hipotezy o symetryczności wyników dwukrotnych pomiarów 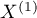 i
i 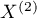 cechy
cechy  (symetryczności 2 zmiennych zależnych
(symetryczności 2 zmiennych zależnych 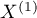 i
i 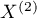 ). Badana cecha może mieć więcej niż 2 kategorie. Test wewnętrznej symetrii Bowker można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach
). Badana cecha może mieć więcej niż 2 kategorie. Test wewnętrznej symetrii Bowker można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach 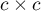 .
.
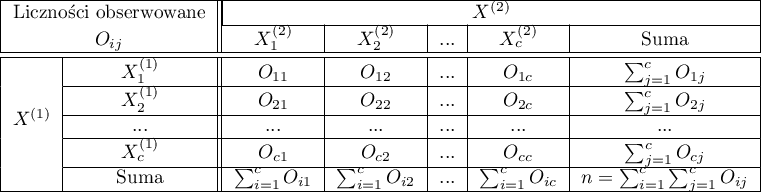
Hipotezy:
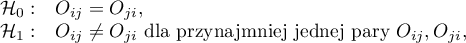
gdzie 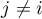 ,
, 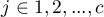 ,
, 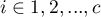 , zatem
, zatem 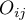 i
i 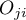 to liczności symetrycznych par w tabeli
to liczności symetrycznych par w tabeli 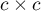
Statystyka testowa ma postać:
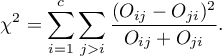
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyliczaną według wzoru 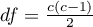 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przeprowadzono 2 badania opinii studentów na temat określonego wykładowcy akademickiego. Oba badania pozwalały ocenić wykładowcę negatywnie, pozytywnie, lub wybrać odpowiedź neutralną - nie mam zdania. Oba badania przeprowadzono na tej samej próbie 250 studentów z tym, że pierwsze badanie dokonano dzień przed egzaminem z przedmiotu prowadzonego przez ocenianego wykładowcę a drugie dzień po egzaminie. Poniżej przedstawiono fragment danych w postaci surowej oraz całość danych w postaci tabeli kontyngencji. Chcemy zbadać, czy obydwa badania dają podobne wyniki.
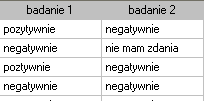

Hipotezy:

gdzie np. zmiana opinii z pozytywnej na negatywną jest symetryczna względem zmiany opinii z negatywnej na pozytywną.
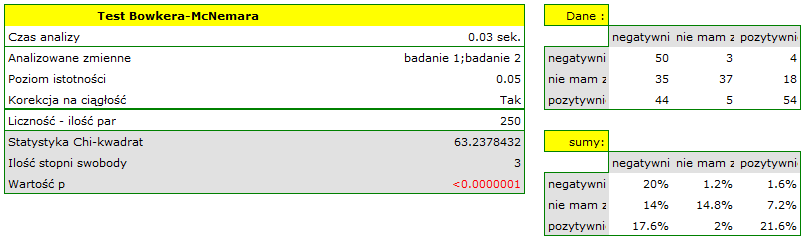
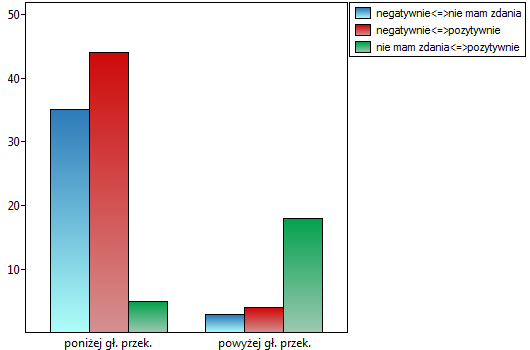
Porównując wartość  dla testu Bowkera
dla testu Bowkera 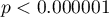 z poziomem istotności
z poziomem istotności  stwierdzamy, że opinie studentów zmieniły się. Z tabeli wynika, że istotnie więcej było tych studentów, którzy zmienili swoją opinię na negatywną po egzaminie niż tych którzy zmienili ją na pozytywną, oraz wielu studentów oceniających przed egzaminem wykładowcę pozytywnie po egzaminie nie wyrażało już takiego zdania.
stwierdzamy, że opinie studentów zmieniły się. Z tabeli wynika, że istotnie więcej było tych studentów, którzy zmienili swoją opinię na negatywną po egzaminie niż tych którzy zmienili ją na pozytywną, oraz wielu studentów oceniających przed egzaminem wykładowcę pozytywnie po egzaminie nie wyrażało już takiego zdania.
Gdybyśmy ograniczyli nasze badanie do osób mających zdefiniowany pogląd na temat wykładowcy (tzn. oceniają tylko pozytywnie lub negatywnie), to moglibyśmy wykorzystać test McNemara:
Hipotezy:

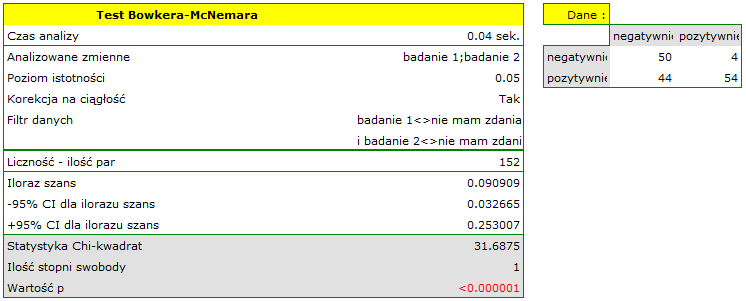
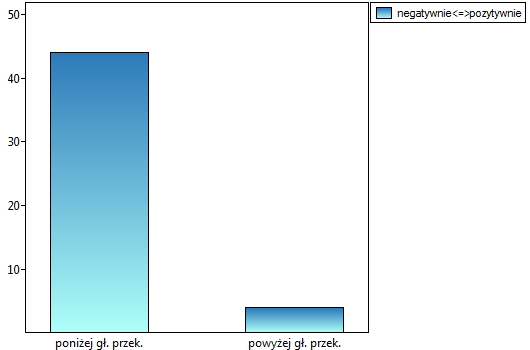
Porównując wartość  dla testu McNemara
dla testu McNemara 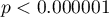 z poziomem istotności
z poziomem istotności  stwierdzamy, że opinie studentów zmieniły się. Istotnie więcej było tych studentów, którzy zmienili swoją opinie na negatywną po egzaminie niż tych którzy zmienili ją na pozytywną. Szansa zmiany opinii z pozytywnej (przed egzaminem) na negatywną (po egzaminie) jest jedenaście
stwierdzamy, że opinie studentów zmieniły się. Istotnie więcej było tych studentów, którzy zmienili swoją opinie na negatywną po egzaminie niż tych którzy zmienili ją na pozytywną. Szansa zmiany opinii z pozytywnej (przed egzaminem) na negatywną (po egzaminie) jest jedenaście 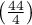 razy większa niż z negatywnej na pozytywną (szansa zmiany opinii w przeciwną stronę to:
razy większa niż z negatywnej na pozytywną (szansa zmiany opinii w przeciwną stronę to: 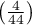 czyli 0.090909).
czyli 0.090909).
2014/08/22 20:00
1)
Mann H. and Whitney D. (1947), On a test of whether one of two random variables is stochastically larger than the other. Annals of Mathematical Statistics, 1 8 , 5 0 4
2)
, 7)
Wilcoxon F. (1949), Some rapid approximate statistical procedures. Stamford, CT: Stamford Research Laboratories, American Cyanamid Corporation
3)
, 8)
Marascuilo L.A. and McSweeney M. (1977), Nonparametric and distribution-free method for the social sciences. Monterey, CA: Brooks/Cole Publishing Company
4)
, 9)
Fritz C.O., Morris P.E., Richler J.J.(2012), Effect size estimates: Current use, calculations, and interpretation. Journal of Experimental Psychology: General., 141(1):2–18.
5)
, 10)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
6)
Wilcoxon F. (1945), Individual comparisons by ranking methods. Biometries, 1, 80-83
11)
Cochran W.G. (1952), The chi-square goodness-of-fit test. Annals of Mathematical Statistics, 23, 315-345
12)
Freeman G.H. and Halton J.H. (1951), Note on an exact treatment of contingency, goodness of fit and other problems of significance. Biometrika 38:141-149
13)
Mehta C.R. and Patel N.R. (1986), Algorithm 643. FEXACT: A Fortran subroutine for Fisher's exact test on unordered r*c contingency tables. ACM Transactions on Mathematical Software, 12, 154–161
14)
Yates F. (1934), Contingency tables involving small numbers and the chi-square test. Journal of the Royal Statistical Society, 1,2 17-235
15)
Fisher R.A. (1934), Statistical methods for research workers (5th ed.). Edinburgh: Oliver and Boyd.
16)
Fisher R.A. (1935), The logic of inductive inference. Journal of the Royal Statistical Society, Series A, 98,39-54
17)
Lancaster H.O. (1961), Significance tests in discrete distributions. Journal of the American Statistical Association 56:223-234
18)
Anscombe F.J. (1981), Computing in Statistical Science through APL. Springer-Verlag, New York
19)
Pratt J.W. and Gibbons J.D. (1981), Concepts of Nonparametric Theory. Springer-Verlag, New York
20)
Plackett R.L. (1984), Discussion of Yates' „Tests of significance for 2×2 contingency tables”. Journal of Royal Statistical Society Series A 147:426-463
21)
Miettinen O.S. (1985), Theoretical Epidemiology: Principles of Occurrence Research in Medicine. John Wiley and Sons, New York
22)
Barnard G.A. (1989), On alleged gains in power from lower p-values. Statistics in Medicine 8:1469-1477
23)
Rothman K.J., Greenland S., Lash T.L. (2008), Modern Epidemiology, 3rd ed. (Lippincott Williams and Wilkins) 221-225
24)
Cochran W.G. (1954), Some methods for strengthening the common chi-squared tests. Biometrics. 10 (4): 417–451
25)
Armitage P. (1955), Tests for Linear Trends in Proportions and Frequencies. Biometrics. 11 (3): 375–386
26)
Bender R. (2001), Calculating confidence intervals for the number needed to treat. Controlled Clinical Trials 22:102–110
27)
, 29)
, 33)
Newcombe R.G. (1998), Interval Estimation for the Difference Between Independent Proportions: Comparison of Eleven Methods. Statistics in Medicine 17: 873-890
28)
, 34)
Wilson E.B. (1927), Probable Inference, the Law of Succession, and Statistical Inference. Journal of the American Statistical Association: 22(158):209-212
30)
Miettinen O.S. and Nurminen M. (1985), Comparative analysis of two rates. Statistics in Medicine 4: 213-226
31)
Beal S.L. (1987), Asymptotic confidence intervals for the difference between two binomial parameters for use with small samples. Biometrics 43: 941-950
32)
Wallenstein S. (1997), A non-iterative accurate asymptotic confidence interval for the difference between two Proportions. Statistics in Medicine 16: 1329-1336
35)
, 36)
Altman D.G. (1998), Confidence intervals for the number needed to treat. BMJ. 317(7168): 1309–1312
37)
McNemar Q. (1947), Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika, 12, 153-157
38)
Rufibach K. (2010), Assessment of paired binary data; Skeletal Radiology volume 40, pages1–4
39)
Fagerland M.W., Lydersen S., and Laake P. (2013), The McNemar test for binary matched-pairs data: mid-p and asymptotic are better than exact conditional, BMC Med Res Methodol; 13: 91
40)
Liddell F.D.K. (1983), Simplified exact analysis of case-referent studies; matched pairs; dichotomous exposure. Journal of Epidemiology and Community Health; 37:82-84
41)
Bowker A.H. (1948), Test for symmetry in contingency tables. Journal of the American Statistical Association, 43, 572-574
statpqpl/porown2grpl/nparpl.txt · ostatnio zmienione: 2020/10/06 14:10 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International