Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown1grpl:nparpl:chigoodnespl
Test chi-kwadrat zgodności
Test  zgodności (dobroci dopasowania) (ang. Chi-square goodnes-of-fit test) nazywany jest również testem
zgodności (dobroci dopasowania) (ang. Chi-square goodnes-of-fit test) nazywany jest również testem  dla pojedynczej próby, przeznaczony jest do testowania zgodności wartości obserwowanych dla
dla pojedynczej próby, przeznaczony jest do testowania zgodności wartości obserwowanych dla  (
(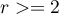 ) kategorii
) kategorii 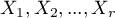 jednej cechy
jednej cechy  z hipotetycznymi wartościami oczekiwanymi dla tej cechy. Wartości wszystkich
z hipotetycznymi wartościami oczekiwanymi dla tej cechy. Wartości wszystkich  pomiarów należy zebrać w postaci tabeli składającej się z
pomiarów należy zebrać w postaci tabeli składającej się z  wierszy (kategorii:
wierszy (kategorii: 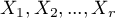 ). Dla każdej kategorii
). Dla każdej kategorii 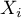 zapisuje się częstość jej występowania
zapisuje się częstość jej występowania 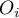 , oraz częstość dla niej oczekiwaną
, oraz częstość dla niej oczekiwaną 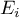 lub prawdopodobieństwo jej wystąpienia
lub prawdopodobieństwo jej wystąpienia 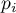 . Częstość oczekiwana jest wyznaczana jako iloczyn
. Częstość oczekiwana jest wyznaczana jako iloczyn 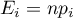 .
.
Utworzona tabela może przyjąć jedną z poniższych postaci:
![LaTeX \begin{tabular}[t]{c@{\hspace{1cm}}c}
\begin{tabular}{c|c c}
Kategorie $X_i$ & $O_i$ & $E_i$ \\\hline
$X_1$ & $O_1$ & $E_i$ \\
$X_2$ & $O_2$ & $E_2$ \\
... & ... & ...\\
$X_r$ & $O_r$ & $E_r$ \\
\end{tabular}
&
\begin{tabular}{c|c c}
Kategorie $X_i$ & $O_i$ & $p_i$ \\\hline
$X_1$ & $O_1$ & $p_1$ \\
$X_2$ & $O_2$ & $p_2$ \\
... & ... & ...\\
$X_r$ & $O_r$ & $p_r$ \\
\end{tabular}
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img53c42b4f4572477f9cbd987271a3d7c9.png)
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
- suma liczności obserwowanych powinna być taka sama jak suma liczności oczekiwanych, a suma wszystkich prawdopodobieństw
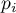 powinna wynosić 1.
powinna wynosić 1.
Hipotezy:
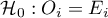 dla wszystkich kategorii,
dla wszystkich kategorii,
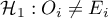 dla przynajmniej jednej kategorii.
dla przynajmniej jednej kategorii.
Statystyka testowa ma postać:
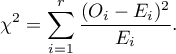 Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru:
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 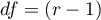 .
.
Wyznaczoną na podstawie wartości statystyki i rozkładu  wartość
wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
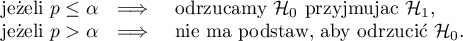
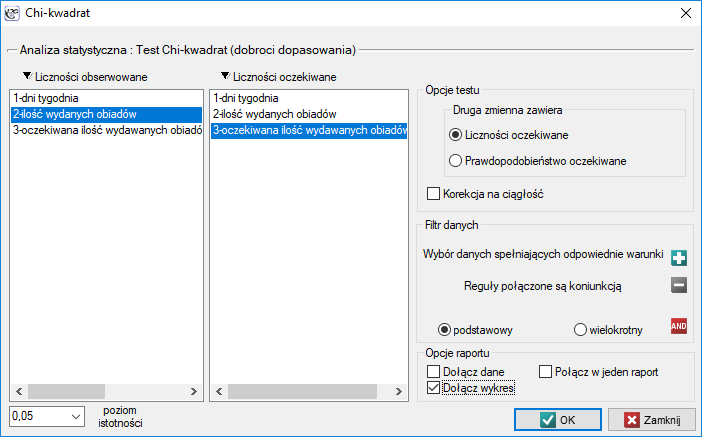
Okno z ustawieniami opcji testu Chi-kwadrat zgodności wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat lub poprzez ''Kreator''.
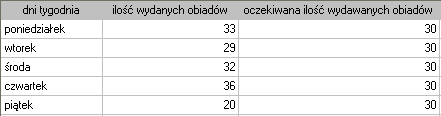
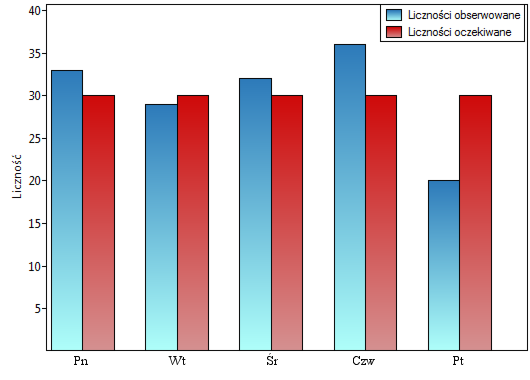
Chcielibyśmy się dowiedzieć, czy liczba wydawanych obiadów w kolejnych dniach tygodnia (od poniedziałku do piątku) w pewnej szkolnej stołówce jest statystycznie taka sama. W tym celu pobrano tygodniową próbę i zapisano dla niej liczbę wydanych obiadów w poszczególnych dniach: poniedziałek - 33, wtorek - 29, środa - 32, czwartek - 36, piątek - 20.}
Łącznie przez cały tydzień (5 dni) wydano 150 obiadów.
Zakładamy, że w każdy dzień prawdopodobieństwo wydania obiadu jest takie samo, czyli wynosi 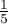 . Oczekiwana liczba wydanych obiadów dla każdego z pięciu dni tygodnia wynosi więc
. Oczekiwana liczba wydanych obiadów dla każdego z pięciu dni tygodnia wynosi więc 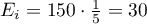 .
.
Postawiono hipotezy:
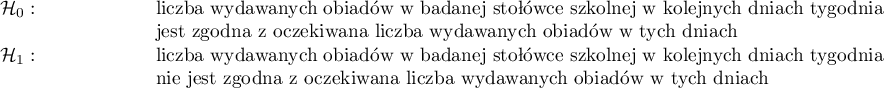
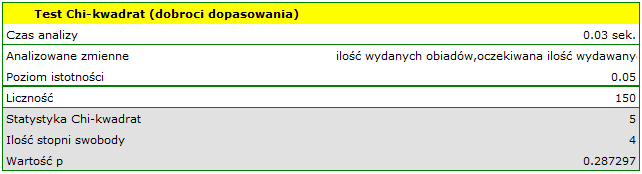
Wartość  z rozkładu
z rozkładu  dla 4 stopni swobody wynosi 0.287297. Zatem na poziomie istotności
dla 4 stopni swobody wynosi 0.287297. Zatem na poziomie istotności  możemy powiedzieć, że nie mamy podstaw, aby odrzucić hipotezę zerową mówiącą o zgodności liczby wydawanych obiadów z oczekiwaną liczbą wydawanych obiadów w poszczególnych dniach.
możemy powiedzieć, że nie mamy podstaw, aby odrzucić hipotezę zerową mówiącą o zgodności liczby wydawanych obiadów z oczekiwaną liczbą wydawanych obiadów w poszczególnych dniach.
Uwaga!
Gdybyśmy chcieli w ramach jednego badania dokonać większej liczby porównań, moglibyśmy zastosować poprawkę Bonferroniego 2) lub inną z poprawek opisanych w dziale Wielokrotne porównania. Ta poprawka jest używana by ograniczyć wielkość popełnionego błędu pierwszego rodzaju, gdy porównujemy wartości obserwowane i oczekiwane pomiędzy wybranymi dniami np:
Pt  Pn,
Pn,
Pt  Wt,
Wt,
Pt  Śr,
Śr,
Pt  Czw,
Czw,
przy założeniu, że porównania wykonujemy niezależnie. Poziom istotności  dla każdego porównania wyznaczamy zgodnie z tą poprawką według wzoru:
dla każdego porównania wyznaczamy zgodnie z tą poprawką według wzoru: 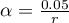 , gdzie
, gdzie  to liczba wykonywanych porównań. Poziom istotności dla pojedynczego porównania zgodnie z poprawką Bonferroniego wynosi dla naszego przykładu
to liczba wykonywanych porównań. Poziom istotności dla pojedynczego porównania zgodnie z poprawką Bonferroniego wynosi dla naszego przykładu 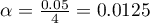 .
.
Należy jednak pamiętać, że redukując  dla każdego porównania zmniejszamy również moc testu.
dla każdego porównania zmniejszamy również moc testu.
statpqpl/porown1grpl/nparpl/chigoodnespl.txt · ostatnio zmienione: 2022/02/11 18:20 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

