PQStat - Baza Wiedzy

Porównywanie krzywych ROC

Bardzo często celem badań jest porównanie wielkości pola pod krzywą ROC (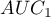 $AUC_1$ ) z polem pod inną krzywą ROC ( 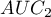$AUC_2$ ). Krzywa ROC o większym polu, pozwala zwykle na dokładniejszą klasyfikację obiektów. Metody służące porównaniu pól zależne są od modelu badania.

Model zależny - porównywane krzywe ROC powstają na bazie pomiarów dokonanych na tych samych obiektach.

Hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & AUC_1=AUC_2, \\ \mathcal{H}_1: & AUC_1\neq AUC_2. \end{array}$

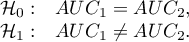
Statystyka testowa ma postać:

$\begin{displaymath} Z=\frac{|AUC_1-AUC_2|}{SE_{AUC_1-AUC_2}}, \end{displaymath}$

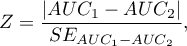
gdzie:

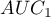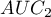$AUC_1$ , $AUC_2$ i błąd standardowy różnicy pól 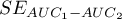$SE_{AUC_1-AUC_2}$ wyliczane są w oparciu o metodę nieparametryczną zaproponowaną przez DeLong (DeLong E.R. i inni 1988¹⁾, Hanley J.A. i Hajian-Tilaki K.O. 1997²⁾)

Statystyka $Z$ ma asymptotycznie (dla dużych liczności) rozkład normalny.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

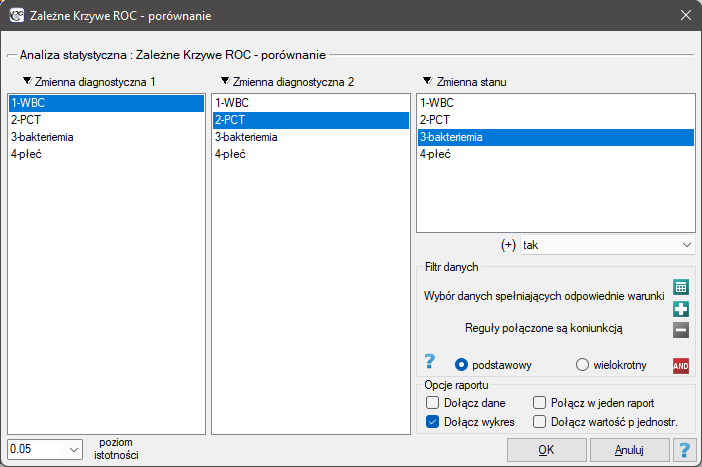
Okno z ustawieniami opcji porównywania zależnych krzywych ROC wywołujemy poprzez menu Statystyka zaawansowana→Testy diagnostyczne→Zależne Krzywe ROC - porównywanie.

Model niezależny - porównywane krzywe ROC powstają na bazie pomiarów dokonanych na różnych obiektach.

Hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & AUC_1=AUC_2, \\ \mathcal{H}_1: & AUC_1\neq AUC_2. \end{array}$

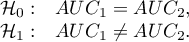
Statystyka testowa (Hanley J.A. i McNeil M.D. 1983³⁾) ma postać:

$\begin{displaymath} Z=\frac{|AUC_1-AUC_2|}{\sqrt{SE_{AUC_1}^2-SE_{AUC_2}^2}}, \end{displaymath}$

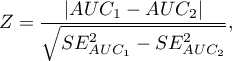
gdzie:

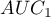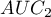$AUC_1$ , $AUC_2$ i błędy standardowe pól 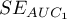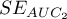$SE_{AUC_1}$ , $SE_{AUC_2}$ wyliczane są w oparciu:

metodę nieparametryczną DeLong (DeLong E.R. i inni 1988⁴⁾, Hanley J.A. i Hajian-Tilaki K.O. 1997⁵⁾) - rekomendowane,
metodę nieparametryczną Hanley-McNeil (Hanley J.A. i McNeil M.D. 1982⁶⁾).

Statystyka $Z$ ma asymptotycznie (dla dużych liczności) rozkład normalny.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

Okno z ustawieniami opcji porównywania niezależnych krzywych ROC wywołujemy poprzez menu Statystyka zaawansowana→Testy diagnostyczne→Niezależne Krzywe ROC - porównywanie.

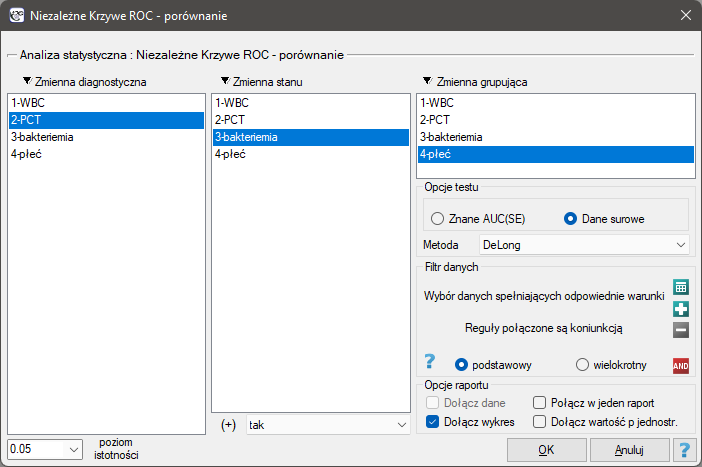
Przykład c.d. (plik bakteriemia.pqs)

Wykonamy 2 porównania:

Zbudujemy 2 krzywe ROC, by porównać wartość diagnostyczną parametrów WBC i PCT;
Zbudujemy 2 krzywe ROC, by porównać wartość diagnostyczną parametru PCT dla chłopców i dziewczynek.

ad1)

Zarówno parametr WBC jak i PCT jest stymulantą (wysokie wartości tych parametrów towarzyszą bakteriemii). Porównując wartość diagnostyczną tych parametrów weryfikujemy hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & $pole pod krzywą ROC dla WBC $=$ pole pod krzywą ROC dla PCT$, \\ \mathcal{H}_1: & $pole pod krzywą ROC dla WBC $\neq $ pole pod krzywą ROC dla PCT$. \end{array}$

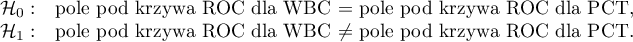
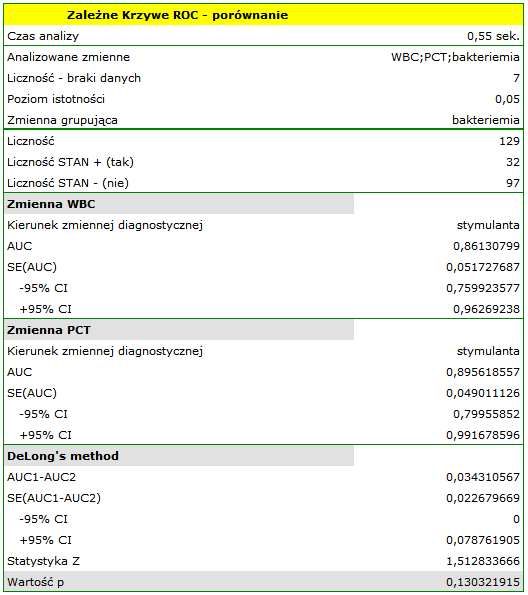
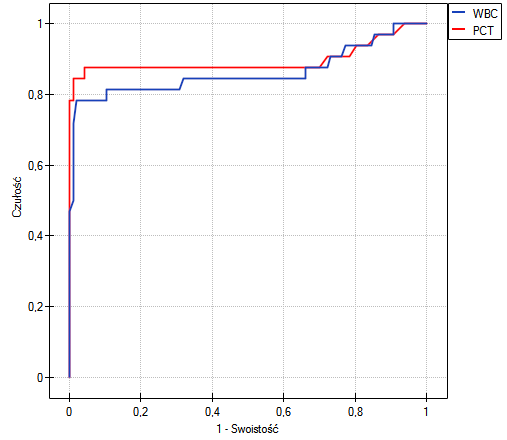
Wyliczone wielkości pól to 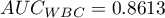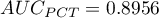$AUC_{WBC}=0.8613$ , $AUC_{PCT}=0.8956$ . Na podstawie przyjętego poziomu $\alpha=0.05$ , w oparciu o uzyskaną wartość $p$ 0.130321915 wnioskujemy, że nie możemy wskazać, który z parametrów WBC czy PCT jest lepszy w rozpoznawaniu bakteriemii.

ad2)

Parametr PCT jest stymulantą (jego wysokie wartości towarzyszą bakteriemii). Porównując jego wartość diagnostyczną dla dziewczynek i chłopców weryfikujemy hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & $pole pod krzywą ROC dla $PCT_k$ $=$ pole pod krzywą ROC dla $PCT_m$$, \\ \mathcal{H}_1: & $pole pod krzywą ROC dla $PCT_k$ $\neq $ pole pod krzywą ROC dla $PCT_m$$. \end{array}$

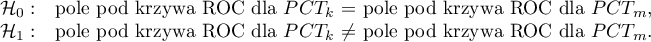
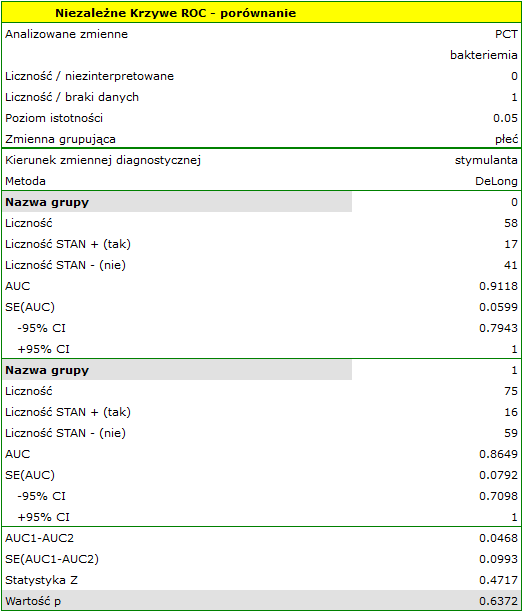
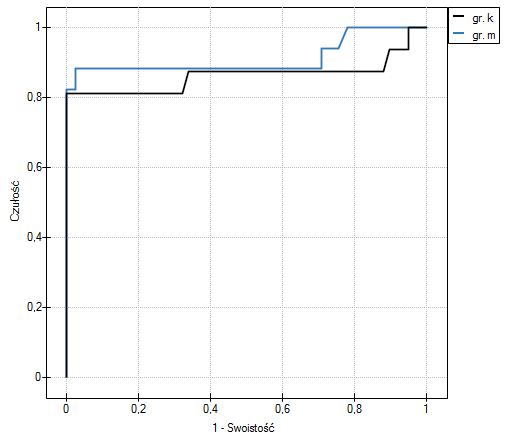
Wyliczone wielkości pól to 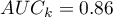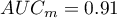$AUC_k=0.86$ , $AUC_m=0.91$ . Zatem na podstawie przyjętego poziomu $\alpha=0.05$ , w oparciu o uzyskaną wartość $p$ =0.6372 wnioskujemy, że nie możemy wybrać płci, dla której parametr PCT jest lepszy w rozpoznawaniu bakteriemii.

¹⁾ , ⁴⁾

DeLong E.R., DeLong D.M., Clarke-Pearson D.L., (1988), Comparing the areas under two or more correlated receiver operating curves: A nonparametric approach. Biometrics 44:837-845

²⁾ , ⁵⁾

Hanley J.A. i Hajian-Tilaki K.O. (1997), Sampling variability of nonparametric estimates of the areas under receiver operating characteristic curves: an update. Academic radiology 4(1):49-58

³⁾

Hanley J.A. i McNeil M.D. (1983), A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 148: 839-843

⁶⁾

Hanley J.A. i McNeil M.D. (1982), The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143(1):29-36

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Porównywanie krzywych ROC

Narzędzia strony