Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:diagnpl:rocpl
Krzywa ROC
 Testem diagnostycznym posługujemy się, by odróżnić obiekty z daną cechą (oznaczone jako (
Testem diagnostycznym posługujemy się, by odróżnić obiekty z daną cechą (oznaczone jako ( ), np. osoby chore) od obiektów bez danej cechy (oznaczone jako (
), np. osoby chore) od obiektów bez danej cechy (oznaczone jako ( ), np. osoby zdrowe). Aby test diagnostyczny mógł być uznany za wartościowy, powinien dawać stosunkowo niewielką liczbę błędnych klasyfikacji. Jeśli test opiera się na zmiennej dychotomicznej, wówczas właściwym narzędziem do oceny jego jakości jest analiza tabeli kontyngencji
), np. osoby zdrowe). Aby test diagnostyczny mógł być uznany za wartościowy, powinien dawać stosunkowo niewielką liczbę błędnych klasyfikacji. Jeśli test opiera się na zmiennej dychotomicznej, wówczas właściwym narzędziem do oceny jego jakości jest analiza tabeli kontyngencji 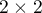 wartości prawdziwie dodatnich (TP), prawdziwie ujemnych (TN), fałszywie dodatnich (FP) i fałszywie ujemnych (FN). Najczęściej jednak testy diagnostyczne opierają się na zmiennych ciągłych lub o uporządkowanych kategoriach. W takiej sytuacji właściwym środkiem oceny zdolności testu do rozróżnienia (
wartości prawdziwie dodatnich (TP), prawdziwie ujemnych (TN), fałszywie dodatnich (FP) i fałszywie ujemnych (FN). Najczęściej jednak testy diagnostyczne opierają się na zmiennych ciągłych lub o uporządkowanych kategoriach. W takiej sytuacji właściwym środkiem oceny zdolności testu do rozróżnienia ( ) i (
) i ( ) są krzywe ROC (ang. Receiver Operating Characteristic).
) są krzywe ROC (ang. Receiver Operating Characteristic).
Często obserwuje się, że wraz ze wzrostem wartości zmiennej diagnostycznej rosną szansę na wystąpienie badanego zjawiska lub odwrotnie: wraz ze wzrostem wartości zmiennej diagnostycznej maleją szansę na wystąpienie badanego zjawiska. Wówczas przy użyciu krzywych ROC dokonuje się wyboru optymalnego punktu odcięcia, czyli pewnej wartości zmiennej diagnostycznej, która najlepiej dzieli badaną zbiorowość na dwie grupy: ( ) w której występuje dane zjawisko i (
) w której występuje dane zjawisko i ( ) w której dane zjawisko nie występuje.
) w której dane zjawisko nie występuje.
Kiedy w oparciu o badania przeprowadzone na tych samych obiektach, są zbudowane dwie lub więcej krzywych ROC, można dokonać porównania tych krzywych pod kątem jakości klasyfikacji.
Załóżmy, że dysponujemy  elementową próbą, w której każdy obiekt uzyskuje jedną z
elementową próbą, w której każdy obiekt uzyskuje jedną z  wartości zmiennej diagnostycznej. Każda z uzyskanych wartość zmiennej diagnostycznej
wartości zmiennej diagnostycznej. Każda z uzyskanych wartość zmiennej diagnostycznej 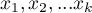 staje sie potencjalnym punktem odcięcia
staje sie potencjalnym punktem odcięcia 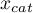 .
.
Jeśli zmienna diagnostyczna to:
- stymulanta (wraz ze wzrostem jej wartości rosną szanse na wystąpienie badanego zjawiska), to wartości większe lub równe punktowi odcięcia (
 ) zaliczamy do grupy (
) zaliczamy do grupy ( );
); - destymulanta (wraz ze wzrostem jej wartości maleją szanse na wystąpienie badanego zjawiska), to wartości mniejsze lub równe punktowi odcięcia (
 ) zaliczamy do grupy (
) zaliczamy do grupy ( ).
).
Dla każdego z  punktów odcięcia wyznaczamy wartości prawdziwie dodatnie (TP), prawdziwie ujemne (TN), fałszywie dodatnie (FP) i fałszywie ujemne (FN).
punktów odcięcia wyznaczamy wartości prawdziwie dodatnie (TP), prawdziwie ujemne (TN), fałszywie dodatnie (FP) i fałszywie ujemne (FN).


Na podstawie tych wartości każdy punkt odcięcia 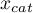 może być dalej opisany za pomocą czułości i swoistości oraz wartości predykcyjnych dodatnich (PPV), wartości predykcyjnych ujemnych (NPV), ilorazu wiarygodności wyniku dodatniego (LR
może być dalej opisany za pomocą czułości i swoistości oraz wartości predykcyjnych dodatnich (PPV), wartości predykcyjnych ujemnych (NPV), ilorazu wiarygodności wyniku dodatniego (LR ), ilorazu wiarygodności wyniku ujemnego (LR
), ilorazu wiarygodności wyniku ujemnego (LR ) i dokładności (Acc).
) i dokładności (Acc).
Uwaga!
Program PQStat na podstawie posiadanej próby wylicza współczynnik chorobowości. Wyliczony współczynnik chorobowości będzie odzwierciedlał występowanie badanego zjawiska (choroby) w populacji, gdy są to badania przesiewowe obejmujące dużą próbę reprezentującą populację. Gdy na badania skierowane są tylko osoby z podejrzeniem choroby, to wyliczony dla nich współczynnik chorobowości może być znacznie wyższy od tego współczynnika w populacji.
Ponieważ zarówno wartość predykcyjna dodatnia jak i ujemna zależy od współczynnika chorobowości, znając a priori ten współczynnik dla populacji, możemy się nim posłużyć by wyliczyć dla każdego punktu odcięcia 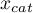 poprawione wartości predykcyjne zgodnie z wzorami Bayesa:
poprawione wartości predykcyjne zgodnie z wzorami Bayesa:
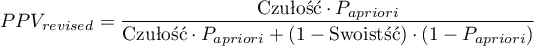
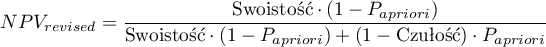
gdzie:
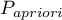 - zadany przez użytkownika współczynnik chorobowości, tzw. pre-test probability of disease
- zadany przez użytkownika współczynnik chorobowości, tzw. pre-test probability of disease

Krzywa ROC powstaje na podstawie wyznaczonych wartości czułości i swoistości. Na osi odciętych umieszczona jest 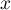 = 1-swoistość, a na osi rzędnych
= 1-swoistość, a na osi rzędnych 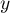 = czułość. Uzyskane punkty są ze sobą połączone. Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną analizowanej zmiennej diagnostycznej. Gdy krzywa ROC pokrywa się z przekątną
= czułość. Uzyskane punkty są ze sobą połączone. Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną analizowanej zmiennej diagnostycznej. Gdy krzywa ROC pokrywa się z przekątną  , to decyzja podejmowana na podstawie zmiennej diagnostycznej jest tak samo dobra jak losowy podział badanych obiektów na grupy (
, to decyzja podejmowana na podstawie zmiennej diagnostycznej jest tak samo dobra jak losowy podział badanych obiektów na grupy ( ) i (
) i ( ).
).
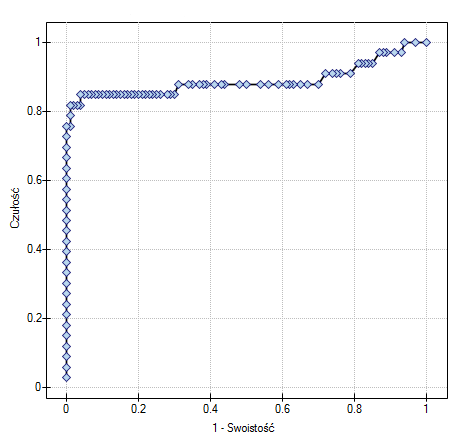
AUC(ang. area under curve) - wielkość pola pod krzywą ROC mieści się w przedziale 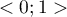 . Im większe jest pole, tym dokładniej zaklasyfikujemy obiekty do grupy (
. Im większe jest pole, tym dokładniej zaklasyfikujemy obiekty do grupy ( ) i (
) i ( ) na podstawie analizowanej zmiennej diagnostycznej. Zatem z tym lepszym skutkiem ta zmienna diagnostyczna może być wykorzystywana jako klasyfikator. Pole
) na podstawie analizowanej zmiennej diagnostycznej. Zatem z tym lepszym skutkiem ta zmienna diagnostyczna może być wykorzystywana jako klasyfikator. Pole 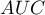 , błąd
, błąd 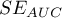 i przedział ufności dla AUC wyliczane są w oparciu:
i przedział ufności dla AUC wyliczane są w oparciu:
- metodę nieparametryczną Hanley-McNeil (Hanley J.A. i McNeil M.D. 19823)),
- metodę Hanley-McNeil zakładającą dwu-ujemny rozkład wykładniczy (Hanley J.A. i McNeil M.D. 19824)) - wyliczną tylko wtedy, gdy grupy (
 ) i (
) i ( ) są równoliczne.
) są równoliczne.
By klasyfikacja była lepsza niż losowy podział obiektów do dwóch klas, pole pod krzywą ROC powinno być istotnie większe niż pole pod prostą  czyli niż 0.5.
czyli niż 0.5.
Hipotezy:
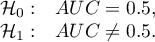
Statystyka testowa ma postać:
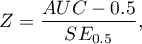
gdzie:
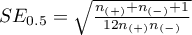 ,
,
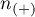 - liczność grupy (
- liczność grupy ( ), w której dane zjawisko rzeczywiście występuje,
), w której dane zjawisko rzeczywiście występuje,
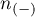 - liczność grupy (
- liczność grupy ( ), w której dane zjawisko rzeczywiście nie występuje.
), w której dane zjawisko rzeczywiście nie występuje.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo, gdy przyjmiemy że parametr diagnostyczny tworzy wysokie pole (AUC), możemy wybrać optymalny punkt odcięcia.
Przykład (plik bakteriemia.pqs)
1)
DeLong E.R., DeLong D.M., Clarke-Pearson D.L., (1988), Comparing the areas under two or more correlated receiver operating curves: A nonparametric approach. Biometrics 44:837-845
2)
Hanley J.A. i Hajian-Tilaki K.O. (1997), Sampling variability of nonparametric estimates of the areas under receiver operating characteristic curves: an update. Academic radiology 4(1):49-58
statpqpl/diagnpl/rocpl.txt · ostatnio zmienione: 2022/02/15 16:17 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

