Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Testy diagnostyczne » Ocena testu diagnostycznego
Pasek boczny
statpqpl:diagnpl:testpl
Ocena testu diagnostycznego
Załóżmy, że przy pomocy testu diagnostycznego badamy występowanie danej cechy (najczęściej choroby) i znamy rzeczywistość (tzw. gold-standard) czyli wiemy, czy ta cecha rzeczywiście występuje u badanych osób. Na podstawie tych informacji możemy zbudować tabelę kontyngencji  :
:

gdzie:
TP - wyniki prawdziwie dodatnie (ang. true positive)
FP - wyniki fałszywie dodatnie (ang. false positive)
FN - wyniki fałszywie ujemne (ang. false negative)
TN - wyniki prawdziwie ujemne (ang. true negative)
Dla takiej tabeli możemy wyliczyć podane niżej miary.
- Czułość i swoistość testu diagnostycznego
Każdy test diagnostyczny może w niektórych przypadkach uzyskać wyniki różne od wyników rzeczywistych, na przykład test diagnostyczny na podstawie otrzymanych parametrów klasyfikuje pacjenta do grupy osób chorych na daną chorobę, bądź zdrowych. W rzeczywistości ilość osób zakwalifikowanych do powyższych grup przez test może się różnić od ilości osób rzeczywiście zdrowych i rzeczywiście chorych.
Stosowane są dwie miary oceny trafności testu diagnostycznego. Są to:
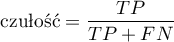
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
* Swoistość (ang. specificity) - opisuje zdolność wykrywania osób rzeczywiście zdrowych (bez danej cechy). Jeśli więc badamy grupę osób zdrowych, to swoistość daje nam informacje jaki procent z nich ma negatywny wynik testu.
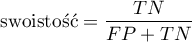
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
- Wartości predykcyjne dodatnie i ujemne oraz współczynnik chorobowości
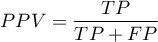
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
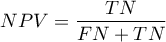
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji. Wartości predykcyjne dodatnie i ujemne są zależne od rozpowszechnienia choroby (od współczynnika chorobowości).
- Współczynnik chorobowości (ang. prevalence) - prawdopodobieństwo wystąpienia choroby w populacji, dla której przeprowadzony był test diagnostyczny.
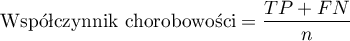
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
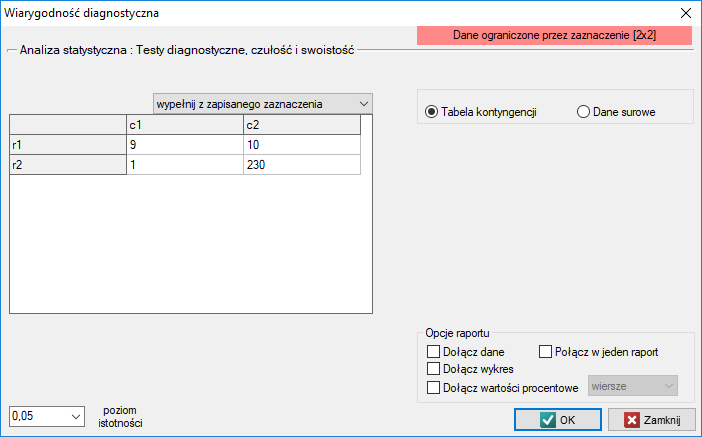
- Iloraz wiarygodności wyniku dodatniego i iloraz wiarygodności wyniku ujemnego
- WypunktowanieIloraz wiarygodności wyniku dodatniego (ang. likelihood ratio of positive test -
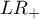 ) - miara ta pozwala na porównywanie dopasowania wyników kilku testów do tzw. gold-standard i nie jest zależna od rozpowszechnienia choroby. Jest to iloraz dwóch szans: szansy na to, że pozytywny wynik testu otrzyma osoba z grupy chorych do szansy, że ten sam efekt będzie obserwowany wśród osób zdrowych.
) - miara ta pozwala na porównywanie dopasowania wyników kilku testów do tzw. gold-standard i nie jest zależna od rozpowszechnienia choroby. Jest to iloraz dwóch szans: szansy na to, że pozytywny wynik testu otrzyma osoba z grupy chorych do szansy, że ten sam efekt będzie obserwowany wśród osób zdrowych.
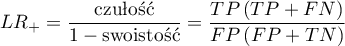
Przedział ufności dla 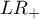 buduje się w oparciu o błąd standardowy:
buduje się w oparciu o błąd standardowy:
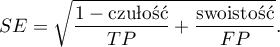
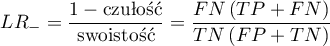
Przedział ufności dla 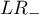 buduje się w oparciu o błąd standardowy:
buduje się w oparciu o błąd standardowy:
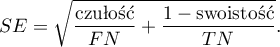
- Dokładność (ang. Accuracy (Acc)) - prawdopodobieństwo prawidłowej diagnozy przy wykorzystaniu testu diagnostycznego. Jeśli więc badana osoba otrzymała pozytywny lub negatywny wynik testu, to
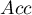 daje jej informację o tym na ile może być pewna postawionej diagnozy.
daje jej informację o tym na ile może być pewna postawionej diagnozy.
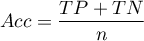
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
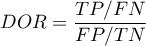
Przedział ufności dla 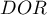 buduje się w oparciu o błąd standardowy:
buduje się w oparciu o błąd standardowy:
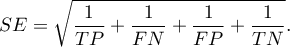
Okno z ustawieniami opcji wiarygodności diagnostycznej wywołujemy poprzez menu Statystyka zaawansowana→Testy diagnostyczne→Wiarygodność diagnostyczna
Przykład (plik mammografia.pqs)
Mammografia jest jednym z najpowszechniej stosowanych testów przesiewowych pozwalających na wykrycie raka piersi. Poniższe badanie zostało przeprowadza na grupie 250 tzw. „bezobjawowych” kobiet w wieku od 40 do 50 lat. Mammografia może wykryć ognisko raka mniejsze niż 5 mm, ale również pozwala stwierdzić zmiany, które nie są jeszcze guzkiem, a jedynie zmianą struktury tkanek. Poniżej przedstawiono przykładowy wynik badania mammograficznego.

Wyznaczymy wartości pozwalające dokonać oceny przeprowadzonego testu diagnostycznego.
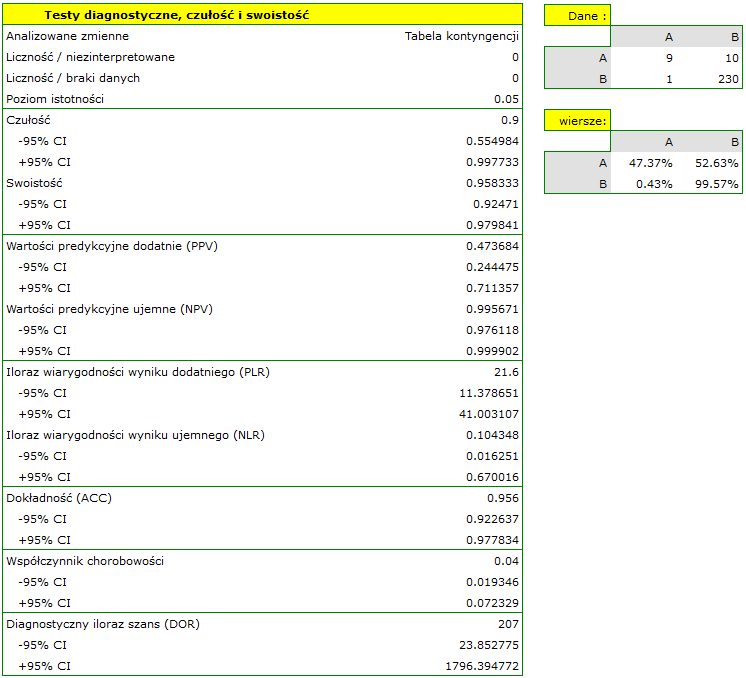
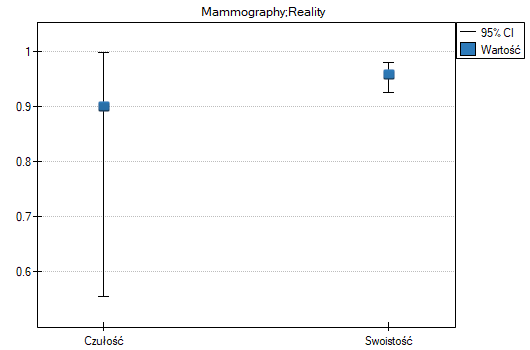
- 90% kobiet chorych na raka piersi zostało poprawnie zdiagnozowanych, czyli uzyskało pozytywny wynik mammografii;
- 95.83% kobiet zdrowych (nie chorujących na raka piersi) zostało poprawnie zdiagnozowanych, czyli uzyskało negatywny wynik mammografii;
- 4 kobiety na 100 przebadanych cierpi z powodu raka piersi;
- Kobieta uzyskująca pozytywny wynik mammografii może być w 47.3% pewna, że ma raka piersi;
- Kobieta uzyskująca negatywny wynik mammografii może być w 99.57% pewna, że nie ma raka piersi;
- WypunktowanieSzansa na to, że pozytywny wynik mammografii otrzyma kobieta rzeczywiście chora na raka jest 21.60 razy większa niż szansa, że pozytywny wynik mammografii otrzyma kobieta rzeczywiście zdrowa (nie chorujących na raka piersi);
- WypunktowanieSzansa na to, że negatywny wynik mammografii otrzyma kobieta rzeczywiście chora na raka stanowi 10.43% szansy na to, że negatywny wynik mammografii otrzyma kobieta rzeczywiście zdrowa (nie chorujących na raka piersi);
- WypunktowanieKobieta poddająca się mammografii (bez względu na uzyskany wynik) może być pewna postawionej diagnozy w 96.50%;
- Szansy na pozytwny wynik testu u kobiety która rzeczywiście choruje na raka piersi jest 207 razy większa od szansy na taki wynik kobiety zdrowej.
statpqpl/diagnpl/testpl.txt · ostatnio zmienione: 2022/09/26 23:30 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

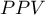 ) - prawdopodobieństwo, że osobnik miał chorobę mając pozytywny wynik testu. Jeśli więc badana osoba otrzymała pozytywny wynik testu, to PPV daje jej informację na ile może być pewna, że cierpi na daną chorobę.
) - prawdopodobieństwo, że osobnik miał chorobę mając pozytywny wynik testu. Jeśli więc badana osoba otrzymała pozytywny wynik testu, to PPV daje jej informację na ile może być pewna, że cierpi na daną chorobę.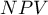 ) - prawdopodobieństwo, że osobnik nie miał choroby mając negatywny wynik testu. Jeśli więc badana osoba otrzymała negatywny wynik testu, to NPV daje jej informację na ile może być pewna, że nie cierpi na daną chorobę.
) - prawdopodobieństwo, że osobnik nie miał choroby mając negatywny wynik testu. Jeśli więc badana osoba otrzymała negatywny wynik testu, to NPV daje jej informację na ile może być pewna, że nie cierpi na daną chorobę.