Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:hotelingpl:hotelling1pl
Test T-kwadrat Hotellinga dla pojedynczej próby
Służy do weryfikacji hipotezy, że  zmiennych w badanej populacji
zmiennych w badanej populacji 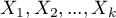 charakteryzuje się średnimi zadanymi przez badacza.
charakteryzuje się średnimi zadanymi przez badacza.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- wielowymiarowy rozkład normalny lub normalność rozkładu każdej badanej zmiennej.
Hipotezy:
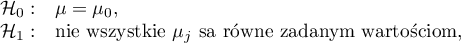
gdzie:
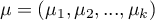 - średnie zmiennych w populacji reprezentowanej przez próbę,
- średnie zmiennych w populacji reprezentowanej przez próbę,
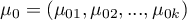 - zadane przez badacza wartości średnich.
- zadane przez badacza wartości średnich.
Statystyka testowa ma postać:
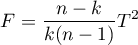
gdzie:
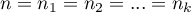 - liczności poszczególnych zmiennych w próbie,
- liczności poszczególnych zmiennych w próbie,
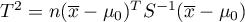 - pierwotna statystyka testowa Hotellinga o rozkładzie
- pierwotna statystyka testowa Hotellinga o rozkładzie  (zalecana dla prób o dużych licznościach),
(zalecana dla prób o dużych licznościach),
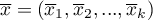 - średnie zmiennych w próbie,
- średnie zmiennych w próbie,
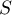 - macierz kowariancji.
- macierz kowariancji.
Statystyka ta podlega rozkładowi F Snedecora z  i
i 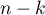 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Gdy po wykonanej analizie szukamy zmiennych, których dotyczą różnice, wyznaczamy jednoczesne przedziały ufności średnich:
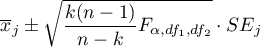
lub przedziały z poprawką Bonferroniego, w celu sprawdzenia czy znajduje się w nich zadana wartość. Jeśli bowiem zadana wartość znajduje się w wyznaczonym przedziale to oznacza, że w rzeczywistości średnia danej zmiennej może być równa tej zadanej wartości. Stosując tą metodę należy jednak pamiętać, że wyznaczone przedziały nie uwzględniają powiązań pomiędzy poszczególnymi zmiennymi (które uwzględnia test Hotellinga) a jedynie wielokrotne testowanie.
Szukając zmiennych, których dotyczą różnice możemy również zastosować podejście jednowymiarowe. Wykonujemy wówczas porównania testem t-Studenta dla pojedynczej próby oddzielnie dla poszczególnych zmiennych. Niestety, nie uwzględnimy tym samym wzajemnych powiązań, ale uzyskane wartości  testu t-Studenta możemy skorygować w dziale Wielokrotne porównania.
testu t-Studenta możemy skorygować w dziale Wielokrotne porównania.
Uwaga!
Zasada działania testu Hotellinga jest tożsama z budową „wielowymiarowej elipsy” przedziałów ufności wokół centrum wyznaczonego przez średnie. Przez co, stosując analizę jednowymiarową (nie uwzględniającą wzajemnych powiązań między zmiennymi) często nie jesteśmy w stanie uzyskać tożsamych wyników.
Przykład - interpretacja elipsy testu Hotellinga dla dwóch zmiennych
Zadany punkt opisany przez wartości średnie (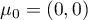 ) znajduje się poza elipsą, co oznacza, że test Hotellinga odrzuca hipotezę
) znajduje się poza elipsą, co oznacza, że test Hotellinga odrzuca hipotezę  , ale stosując podejście jednowymiarowe (przedziały ufności dla każdej zmiennej oddzielnie) nie jesteśmy w stanie odrzucić hipotezy
, ale stosując podejście jednowymiarowe (przedziały ufności dla każdej zmiennej oddzielnie) nie jesteśmy w stanie odrzucić hipotezy  , by wskazać zmienną, której dotyczą różnice.
, by wskazać zmienną, której dotyczą różnice.
(0.5,2)
\psline[linecolor=red]{<->}(1.5,-0.3)(1.5,3.25)
\psline[linecolor=red]{<->}(-1.6,-0.7)(0.55,-0.7)
\rput[b]{90}(1.7,1.4){\textcolor{red}{\psframebox*{\tiny $95\%CI (\mu_2)$}}}
\rput(-0.5,-0.7){\textcolor{red}{\psframebox*{\tiny $95\%CI (\mu_1)$}}}
\rput(-2,2.3){\scriptsize elipsa przedziału}
\rput(-2,2){\scriptsize ufności dla średnich}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgdf1b106bb83a542be98c4ca58398239d.png)
Okno z ustawieniami opcji testu Hotellinga dla pojedynczej próby wywołujemy poprzez menu Statystyka→Testy parametryczne→T-kwadrat Hotellinga
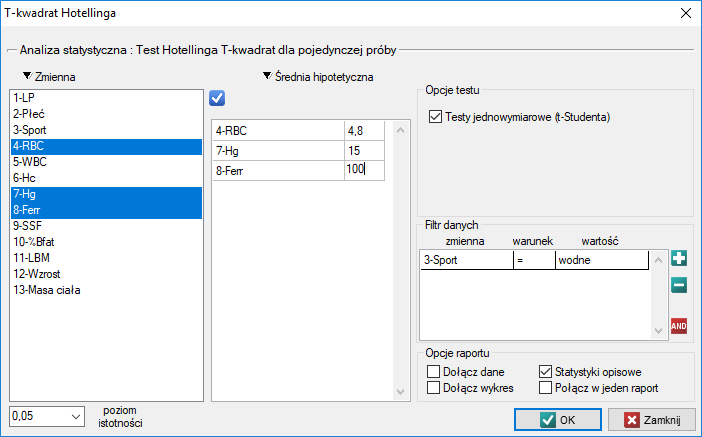
Przebadano grupę sportowców by uzyskać informację między innymi o takich parametrach zdrowotnych jak:
RBC - Liczba czerwonych krwinek,
Hg - Hemoglobina [g/dl],
Ferr - Ferrytyna [µg/l].
Chcemy wiedzieć, na ile bliskie oczekiwanym przez badaczy wartościom są średnie poziomy RBC, hemoglobiny i ferrytyny dla sportowców uprawiających tzw. sporty „wodne”. Oczekiwane średnie to:
RBC = 4.8,
Hg = 15[g/dl],
Ferr = 100[µg/l].
Hipotezy:

Ponieważ arkusz danych zawiera informacje o badanych parametrach dla większej grupy sportowców, w oknie analizy osoby, które uprawiają sporty wodne wskazujemy poprzez filtr danych.
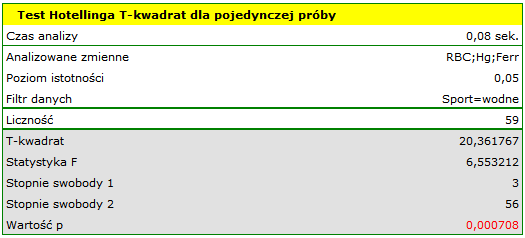
Porównując wartość  z poziomem istotności
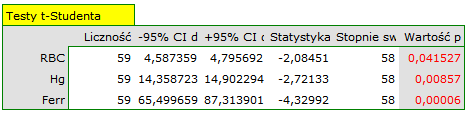
z poziomem istotności  stwierdzamy, że średnie poziomy badanych parametrów różnią się od wartości zadanej. Różnic możemy poszukiwać w wyznaczonych jednoczesnych przedziałach ufności lub w przedziałach z korektą Bonferroniego. Dla ferrytyny jednoczesny 95% przedział ufności znajduje się poniżej zadanej wartości, co świadczy o niższej populacyjnej wartości ferrytyny niż zadana przez badaczy. Przedział dla RBC i hemoglobiny zawiera zadane wartości, co wskazuje na brak istotnych statystycznie różnic.
stwierdzamy, że średnie poziomy badanych parametrów różnią się od wartości zadanej. Różnic możemy poszukiwać w wyznaczonych jednoczesnych przedziałach ufności lub w przedziałach z korektą Bonferroniego. Dla ferrytyny jednoczesny 95% przedział ufności znajduje się poniżej zadanej wartości, co świadczy o niższej populacyjnej wartości ferrytyny niż zadana przez badaczy. Przedział dla RBC i hemoglobiny zawiera zadane wartości, co wskazuje na brak istotnych statystycznie różnic.

Nieco węższe przedziały uzyskamy wykorzystując poprawkę Bonferroniego, wówczas nie tylko przedział dla ferrytyny znajduje się poniżej przedziału ufności ale również przedział dla hemoglobiny.

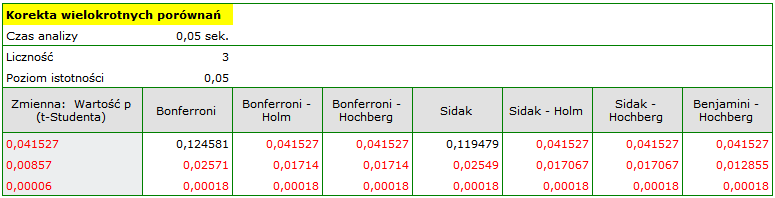
Podejście jednowymiarowe ze względu na swoją prostotę wykorzystywane jest najczęściej. Możemy tu wybrać mniej konserwatywne korekty wielokrotnych porównań niż poprawka Bonferroniego lub Sidaka, uzyskując w ten sposób różnice dotyczące wszystkich badanych parametrów.
By wykonać korektę wartości  testu t-Studenta należy przekopiować te wartości do jednej kolumny nowego arkusza danych i z menu
testu t-Studenta należy przekopiować te wartości do jednej kolumny nowego arkusza danych i z menu Statystyka wybrać Korektę wielokrotnych porównań.
statpqpl/hotelingpl/hotelling1pl.txt · ostatnio zmienione: 2022/01/23 21:07 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

