Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:hotelingpl:boxpl
Test Box'a równości macierzy kowariancji
Test ten służy do porównania dwóch lub więcej ( ) macierzy kowariancji opisujących niezależne populacje.
) macierzy kowariancji opisujących niezależne populacje.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- wielowymiarowy rozkład normalny w badanych populacjach lub normalność rozkładu każdej badanej zmiennej w każdej populacji,
Hipotezy:
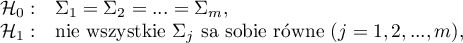
gdzie:
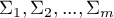 - populacyjne macierze kowariancji.
- populacyjne macierze kowariancji.
Statystyka testowa ma postać:
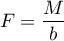
gdzie:
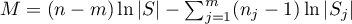 ,
,
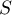 - wspólna (ang. pooled) macierz kowariancji,
- wspólna (ang. pooled) macierz kowariancji,
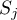 - macierz kowariancji dla
- macierz kowariancji dla  -tej próby,
-tej próby,
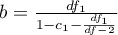 ,
,
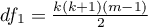 ,
,
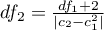 ,
,
 - liczba analizowanych zmiennych,
- liczba analizowanych zmiennych,
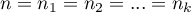 - liczności poszczególnych zmiennych w próbie.
- liczności poszczególnych zmiennych w próbie.
Statystyka ta podlega rozkładowi F Snedecora z 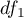 i
i 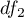 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Należy pamiętać, że test Box'a jest szczególnie wrażliwy na złamanie założenia normalności rozkładu.
Test Box'a jest wyliczany opcjonalnie w Hotellingu dla grup niezależnych lub w analizie MANOVA.
Przykład c.d. (plik sport.pqs)
statpqpl/hotelingpl/boxpl.txt · ostatnio zmienione: 2022/01/23 21:08 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

