PQStat - Baza Wiedzy

Test Fishera-Snedecora

Test Fishera-Snedecora (ang. F-Snedecor test) opiera się na zmiennej 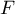$F$ sformułowanej przez Fishera (1924), a jej rozkład opisał Snedecor. Test ten służy do weryfikacji hipotezy o równości wariancji badanej zmiennej w dwóch populacjach.

Podstawowe warunki stosowania:

pomiar na skali interwałowej,
normalność rozkładu badanej zmiennej w obu populacjach,
model niezależny.

Hipotezy:

$\begin{array}{cc} \mathcal{H}_0: & \sigma_1^2=\sigma_2^2,\\ \mathcal{H}_1: & \sigma_1^2\ne\sigma_2^2, \end{array}$

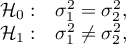
gdzie:

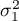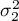
$\sigma_1^2$ , $\sigma_2^2$ $-$ wariancje badanej zmiennej w pierwszej i drugiej populacji.

Statystyka testowa ma postać: $\begin{displaymath} F=\displaystyle{\frac{sd_1^2}{sd_2^2}}, \end{displaymath}$

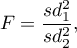
gdzie:

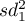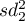
$sd_1^2$ , $sd_2^2$ $-$ wariancje badanej zmiennej w próbach wybranych losowo z pierwszej i drugiej populacji.

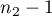Statystyka ta podlega rozkładowi F Snedecora z $n_1-1$ i $n_2-1$ stopniami swobody.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

Okno z ustawieniami opcji testu F Fishera-Snedecora wywołujemy poprzez menu Statystyka→Testy parametryczne→F Fisher Snedecor.

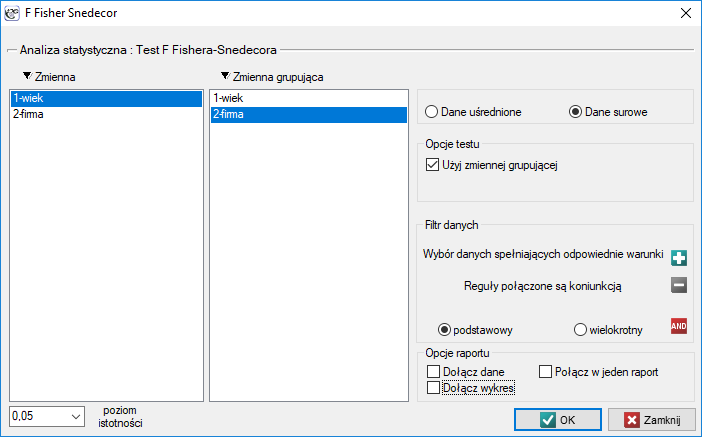
Uwaga!

Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. odchyleniach standardowych i liczności prób.

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Test Fishera-Snedecora

Narzędzia strony