Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown2grpl:parpl:t_test2zalcpl
Test t-Studenta dla grup zależnych
Test t-Studenta dla grup zależnych (ang. t test for dependent groups) stosuje się w sytuacji gdy pomiarów badanej zmiennej dokonujemy dwukrotnie w różnych warunkach (przy czym zakładamy, że wariancje zmiennej w obu pomiarach są sobie bliskie). Interesuje nas różnica pomiędzy parami pomiarów (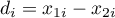 ). Różnica ta wykorzystywana jest do weryfikacji hipotezy o tym, że średnia dla niej (dla różnicy) w badanej populacji wynosi 0.
). Różnica ta wykorzystywana jest do weryfikacji hipotezy o tym, że średnia dla niej (dla różnicy) w badanej populacji wynosi 0.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu różnicy pomiarów
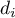 ,
,
Hipotezy:
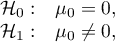
gdzie:
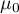 ,
,  średnia różnic
średnia różnic 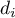 w populacji.
w populacji.
Statystyka testowa ma postać:
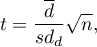
gdzie:
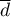
 średnia różnic
średnia różnic 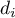 w próbie,
w próbie,
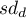
 odchylenie standardowe różnic
odchylenie standardowe różnic 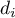 w próbie,
w próbie,

 liczność różnic
liczność różnic 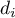 w próbie.
w próbie.
Statystyka testowa ma rozkład t-Studenta z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
- odchylenie standardowe różnicy wyraża się wzorem:
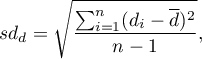
- błąd standardowy średniej różnic wyraża się wzorem:
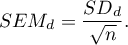
Standaryzowana wielkość efektu.
Współczynnik d-Cohena określa jak dużą częścią występującej zmienności jest różnica między średnimi, biorąc pod uwagę skorelowanie zmiennych.
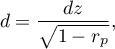 .
.
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 1) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
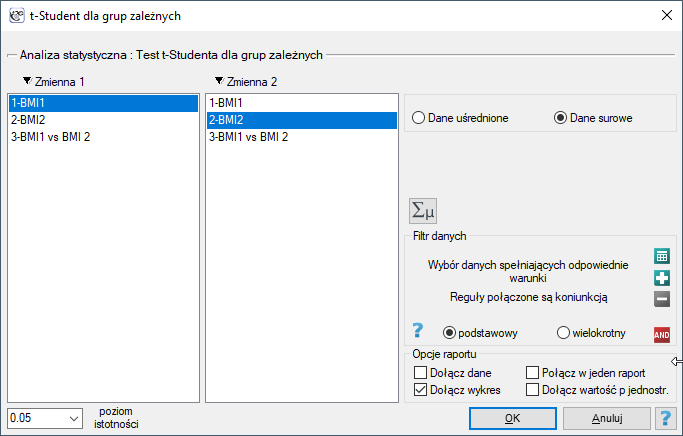
Okno z ustawieniami opcji testu t-Studenta dla grup zależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→t-Student dla grup zależnych lub poprzez ''Kreator''.
Uwaga!
Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. średniej różnic, odchyleniu standardowym różnic i liczności próby.
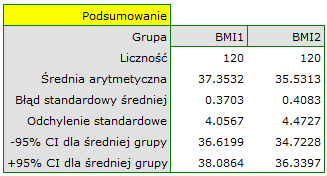
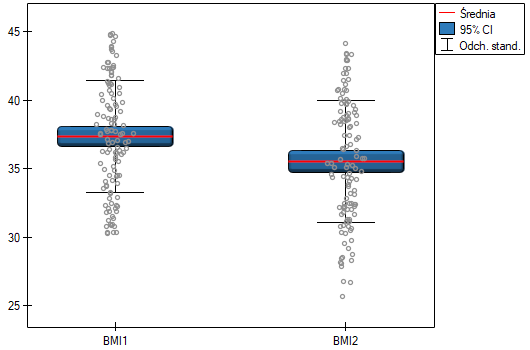
W klinice leczącej zaburzenia odżywiana badano wpływ zalecanej „diety A” na zmianę masy ciała. Próbę 120 otyłych chorych poddano diecie. Zbadano dla nich poziom BMI dwukrotnie: przed wprowadzeniem diety i po 180 dniach stosowania diety. By sprawdzić skuteczność diety porównano uzyskane wyniki pomiarów BMI.
Hipotezy:
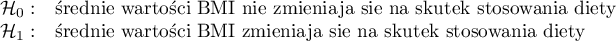

Porównując wartość 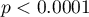 z poziomem istotności
z poziomem istotności  stwierdzamy, że średni poziom BMI zmienił się istotnie. Przed stosowaniem diety był wyższy średnio o niecałe 2 jednostki.
stwierdzamy, że średni poziom BMI zmienił się istotnie. Przed stosowaniem diety był wyższy średnio o niecałe 2 jednostki.
W badaniu możliwe było stosowanie testu t-Studenta dla grup zależnych, ponieważ rozkład różnicy pomiędzy parami pomiarów był rozkładem normalnym (test Lillieforsa, wartość 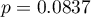 ).
).
1)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
statpqpl/porown2grpl/parpl/t_test2zalcpl.txt · ostatnio zmienione: 2022/09/13 22:46 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

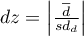 ,
,
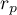 –
– 