Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:metapl:heterog
Badanie heterogeniczności
Trudno oczekiwać by każde badanie kończyło się uzyskaniem dokładnie tej samej wielkości efektu. W naturalny sposób uzyskane w różnych pracach wyniki będą nieco inne. Badanie heterogeniczności ma ustalić na ile pojawiające się różnice pomiędzy uzyskanymi w różnych pracach efektami mają wpływ na budowany w meta-analizie efekt sumaryczny. Efekt sumaryczny dobrze podsumowuje wyniki uzyskane w poszczególnych pracach, jeśli różnice między poszczególnymi efektami są naturalne tzn. nieduże. Duże różnice w obserwowanych efektach mogą świadczyć o niejednorodności badań i konieczności wydzielenia bardziej homogenicznych podgrup np. podzielenia zebranych prac na kilka podgrup względem dodatkowego czynnika. Dla przykładu: dany lek inaczej działa na osoby młodsze a inaczej na starszych, więc w pracach opartych na danych pochodzących głównie od osób młodych uzyskiwany efekt może znacznie odbiegać od prac przeprowadzanych na osobach starszych. Podzielenie zebranych prac na bardziej jednorodne podgrupy pozwoli na dobre oszacowanie efektu sumarycznego dla każdej z tych podgrup oddzielnie.
Badanie heterogeniczności ma na celu sprawdzenie czy zmienność pomiędzy badaniami jest zerowa.
Hipotezy:
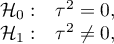
gdzie:
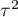 - to wariancja prawdziwych (populacyjnych) efektów poszczególnych badań.
- to wariancja prawdziwych (populacyjnych) efektów poszczególnych badań.
Statystyka testowa ma postać:
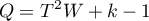
gdzie:
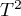 - to wariancja obserwowanych efektów,
- to wariancja obserwowanych efektów,
 - współczynnik wyliczony na podstawie wag przypisanych do poszczególnych badań,
- współczynnik wyliczony na podstawie wag przypisanych do poszczególnych badań,
 - liczba badań.
- liczba badań.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyliczaną według wzoru: 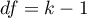 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności poziomem istotności
porównujemy z poziomem istotności poziomem istotności  :
:

Uwaga!
- Jeśli uzyskamy wynik jest istotny statystycznie - jest to mocna sugestia, by zrezygnować z wspólnego podsumowywania wszystkich zebranych badań.
- Jeśli uzyskany wynik jest nieistotny statystycznie - możemy podsumować badania wspólnym efektem. Przy czym sugeruje się, by podsumowania dokonywać zwykle efektem zmiennym - zgodnie z poniższym uzasadnieniem.
Uzasadnienie wyboru efektu zmiennego:
Podsumowanie badania efektem zmiennym bierze pod uwagę zmienność pomiędzy badaniami (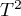 ), natomiast podsumowanie efektem stałym nie bierze pod uwagę tej zmienności. Jeśli jednak
), natomiast podsumowanie efektem stałym nie bierze pod uwagę tej zmienności. Jeśli jednak 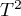 jest małe, to wynik działania modelu z efektem stałym będzie bliski wynikom działania modelu z efektem zmiennym, a gdy
jest małe, to wynik działania modelu z efektem stałym będzie bliski wynikom działania modelu z efektem zmiennym, a gdy 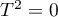 , oba modele dadzą dokładnie ten sam wynik.
, oba modele dadzą dokładnie ten sam wynik.
Dodatkowymi miarami opisującymi heterogeniczność są współczynniki 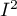 i
i 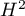 :
:
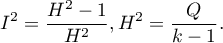
Współczynnik 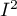 określa procent obserwowanej wariancji, jaki wynika z rzeczywistej różnicy w wielkości badanych efektów (graficznie, odzwierciedla stopień zazębiania się przedziałów ufności poszczególnych badań). Ze względu na to, że mieści się on pomiędzy 0% a 100%, podlega prostej interpretacji i jest chętnie stosowany. Jeśli
określa procent obserwowanej wariancji, jaki wynika z rzeczywistej różnicy w wielkości badanych efektów (graficznie, odzwierciedla stopień zazębiania się przedziałów ufności poszczególnych badań). Ze względu na to, że mieści się on pomiędzy 0% a 100%, podlega prostej interpretacji i jest chętnie stosowany. Jeśli 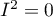 , wówczas cała obserwowana wariancja wielkości efektów jest „fałszywa”, więc jeśli w wyznaczonym wokół współczynnika
, wówczas cała obserwowana wariancja wielkości efektów jest „fałszywa”, więc jeśli w wyznaczonym wokół współczynnika 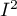 przedziale ufności znajdzie się wartość 0, uzyskaną wariancję można uznać za nieistotną statystycznie. Natomiast czym wartość
przedziale ufności znajdzie się wartość 0, uzyskaną wariancję można uznać za nieistotną statystycznie. Natomiast czym wartość 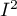 jest bliższa 100%, tym bardziej należy się zastanowić nad rezygnacją z wspólnego podsumowania badań. Przyjmuje się, że
jest bliższa 100%, tym bardziej należy się zastanowić nad rezygnacją z wspólnego podsumowania badań. Przyjmuje się, że 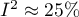 oznacza słabą,
oznacza słabą, 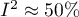 średnią, a
średnią, a 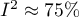 silną heterogeniczność badań. Współczynnik
silną heterogeniczność badań. Współczynnik 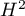 rozpatruje się natomiast w odniesieniu do wartości 1. Jeśli przedział ufności dla
rozpatruje się natomiast w odniesieniu do wartości 1. Jeśli przedział ufności dla 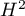 zawiera wartość 1, wówczas uzyskaną wariancję można uznać za nieistotną statystycznie, a im wyższa wartość
zawiera wartość 1, wówczas uzyskaną wariancję można uznać za nieistotną statystycznie, a im wyższa wartość 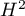 , tym większa heterogeniczność badań.
, tym większa heterogeniczność badań.
Przykład c.d. (plik MetaanalizaRR.pqs)
Badając wpływ palenia papierosów na wystąpienie choroby X sprawdzono założenie dotyczące heterogeniczności badań. W tym celu, w oknie analizy wybrano opcję Badanie heterogeniczności.

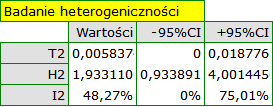
Uzyskano istotny statystycznie wynik statystyki Q (p=0.04284). Wariancja obserwowanych efektów nie jest zerowa (T2=0.0058), a współczynnik I2=48.27%, wskazuje na przeciętną heterogeniczność badań. Jedynie przedział ufności dla współczynnika H2 uznaje za nieistotną zmienność pomiędzy badaniami (przedział dla tego współczynnika to [0.93-4.00]). Mając na uwadze powyższe wyniki, należy się zastanowić, czy zebrane prace mogą być podsumowane jednym wspólnym efektem końcowym (wspólnym relatywnym ryzykiem), czy też warto wyznaczyć bardziej homogeniczną grupę prac i przeprowadzić analizę ponownie.
statpqpl/metapl/heterog.txt · ostatnio zmienione: 2020/11/05 12:22 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

